На Хабре было уже много статей, посвящённых быстрым вычислениям тригонометрии, когда сильно надо, но я хотел бы дополнить их одной небольшой заметкой с отсылкой к школьной тригонометрии.
Иногда может не быть аппаратной реализации тригонометрии, иногда могут быть иные причины, чтобы изобретать методы ускорения вычисления.
Математика
Давайте вспомним некоторые простые формулы из школьного курса.
Начнём с простых:
(1)
sin x = cos (90° - x)cos x = sin (90° - x)sin -x = -sin xcos -x = cos x- В общем случае
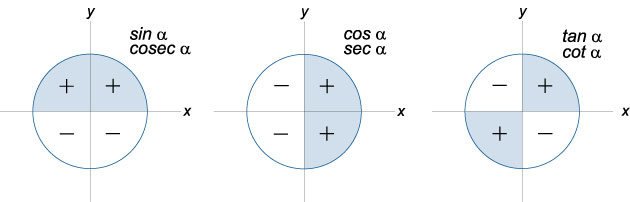
sin (90°N ± x) = ±cos xдля нечётных N и±sin xдля чётных. Знак берётся исходя из знака аргумента в соответствующей четверти круга.
Дальше:
(2)
cos (x + y) = cos x cos y - sin x sin ysin (x + y) = sin x cos y + cos x sin y
И ещё:
(3)
sin x = x - x^3/3! + x^5/5! - ...cos x = 1 - x^2/2! + x^4/4! - ...
Косинус/синус любого угла может быть приведён к аргументу в диапазоне от 0° до 45°, используя формулы первой группы.
Для малых углов тригонометрические функции могут быть сведены к асимптотическим разложениям, если отбрасываемые члены заведомо выходят за разрядную сетку.
Все промежуточные углы могут быть получены суммированием больших углов с некоторым шагом (а для них тригонометрию можно считать таблично), и остатков, которые рано или поздно дадут линейное разложение.
Применение
Предположим, что мы работаем с числами одинарной точности IEEE-754 они имеют имена float, single и т.п. В мантиссе 23 знака, значит нам надо получить относительную погрешность 2^-23.
Давайте оценим, как глубоко надо опуститься, чтобы построить таблицы аргументов.
Для синуса будем отбрасывать кубический член, поэтому нам нужно, чтобы его отношение к линейному было меньше чем допустимая погрешность, откуда выходит, что: 1 - (x - x^3/3!) / x = x^2/6должно быть меньше 2^-23, откуда следует, что для аргументов не более чем 0.000846 радиана нам достаточно точности приближенного вычисления для синуса. Для косинуса, если отбрасывать квадратичный член, нужна точность примерно в 2 раза лучше — 0.000488 радиана.
Итак, нам не надо иметь табличные значения для аргумента меньше чем 0.000488 радиана.
Для построения таблицы перенормируем входной аргумент так, чтобы значению 0 соответствовал угол 0°, а для значения 1 — угол 45°, или pi/4=0.78539816 радиан. Тогда минимальный угол, полученный выше, будет пересчитан в 0.0006217 радиан, или примерно 1/1600 — это больше чем 1/2048 = 2^-11.
Дальше нужно будет выбрать шаг таблиц исходя из того, как мы хотим распределить вычисления, показатель степени 11 мы разделим на несколько частей. Например, можно разбить его на две части: 11=6+5, тогда нам понадобятся две таблицы размером 64 и 32 записи (итого 96), или на три части: 11=4+4+3 (размер таблиц 16+16+8=40 записей), но будет больше операций умножения — конкретный выбор будет зависеть от задачи и располагаемых ресурсов.
Ремарка: запись в таблице — это пара синус и косинус аргумента. Если храним с одинарной точностью, то размер записи 8 байт.
Пример
Давайте для примера возьмём разложение 4+4+3, а потом обобщим.
Итак, задача: вычислить значение sin x для произвольного x.
Шаг 1. Приведём аргумент x к нашей шкале, поделив его на константу pi/4 (назовём его x').
Шаг 2. В зависимости от значения аргумента x' используя формулы (1) выберем нужную функцию таким образом, чтобы аргумент её был в диапазоне от 0 до 1 (включительно) (назовём x''. На этом шаге также нужно будет отметить знак получаемого результата.
[предположим для примера, что получился синус]
Шаг 3. Воспользуемся таблицами (напомню, что их 3), при этом индексами в таблице будут "битовые поля" в двоичном представлении аргумента x'' — первые 4 бита после запятой, потом ещё 4, и ещё 3, а оставшиеся не при делах биты пойдут в остаток.
Табличные синус назовём S1, S2, S3, табличные косинусы — C1, C2, C3.
Поскольку угол мы делили на pi/4, то чтобы получить остаток в радианах, его надо умножить на эту же величину. "Битовый" остаток, умноженный pi/4, обозначим как A. Тогда его синус будет равен A, а косинус — 1.
Шаг 4. Объединяем всё, что получилось:
C12 = C1 C2 - S1 S2
S12 = S1 C2 + C1 S2
C123 = C12 C3 - S12 S2
S123 = S12 C3 + C12 S3|sin x| = S123 + C123 A (если на шаге 2 получили синус)
|sin x| = C123 - S123 A (если на шаге 2 получили косинус)
Шаг 5. Если на шаге 2 мы сочли, что результат должен получиться отрицательным, то этот минус надо ввести в результат.
Заключение
Аналогичный подход может использоваться как для вычисления в вещественных числах любого размера, так и, например, для реализации специализированной арифметики с фиксированной запятой. Собственно, в своё время именно последняя задача меня и сподвигла поковыряться в эту сторону, но это было давно.








