В одной из прошлых статей с подозрительно похожим заголовком мы показали, как построить модель месторождения и посчитать свойства пласта глубоко под землёй, используя крохи информации о породе, полученной со скважин.
В этой статье мы расскажем, как отобразить модель месторождения на экране так, чтобы опытные геологи и гидродинамики могли сразу видеть (не)соответствие модели своим знаниям об особенностях конкретного месторождения.
Более того, вся реализация займёт у нас не больше часа – после чего мы сможем визуализировать практически любые реальные модели месторождений, как на картинке. А в следующей статье мы оптимизируем быстродействие и потребление видеопамяти настолько, что наш рендерер станет самым быстрым и эффективным в мире*.
* среди известных авторам.
Дисклеймер: эта статья не является пособием по 3D-рендерингу и графическому API. Всё, что требуется от читателя – это понимание основных принципов 3D-графики: что такое атрибуты вершин и т. п. К счастью, на Хабре есть множество хороших статей (раз, два), которые можно прочитать для освежения этих концепций в памяти. В этой статье мы использовали современный OpenGL 4.5, но всё описанное будет работать даже на древнем OpenGL (ES) 2.0.
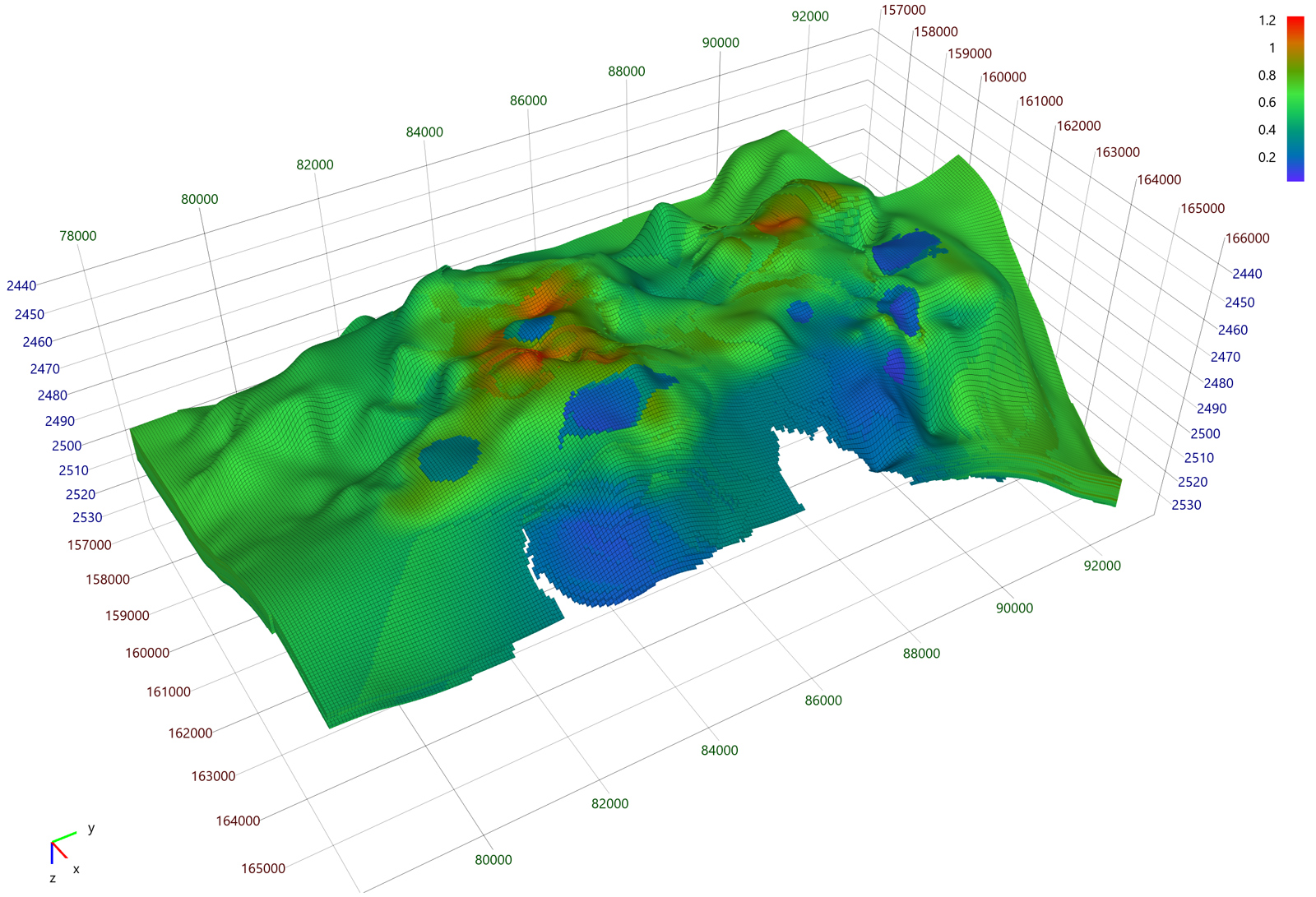
На картинке в начале статьи представлена типичная модель месторождения, которая совсем не похожа на регулярную воксельную сетку, как в Майнкрафте.
Подобные сетки, называемые геометрией угловой точки (англ. Corner-Point Grid/Geometry), уже более 30 лет используются практически в любом софте для геологического и гидродинамического моделирования. В простонародье ГУТ часто называют угловой геометрией.
Геометрия угловой точки даёт возможность довольно точно моделировать разломы в пласте – намного точнее регулярных сеток. Благодаря своим ограничениям, угловая геометрия требует гораздо меньше памяти для хранения сетки, чем полностью нерегулярная сетка. Как оказалось, эти же ограничения позволяют значительно оптимизировать производительность рендеринга – что и даёт нам право без зазрения совести утверждать, что такой визуализацией можно пользоваться на сравнительно маломощных интегрированных в процессор видеокартах. Но об этом мы расскажем во второй части статьи.
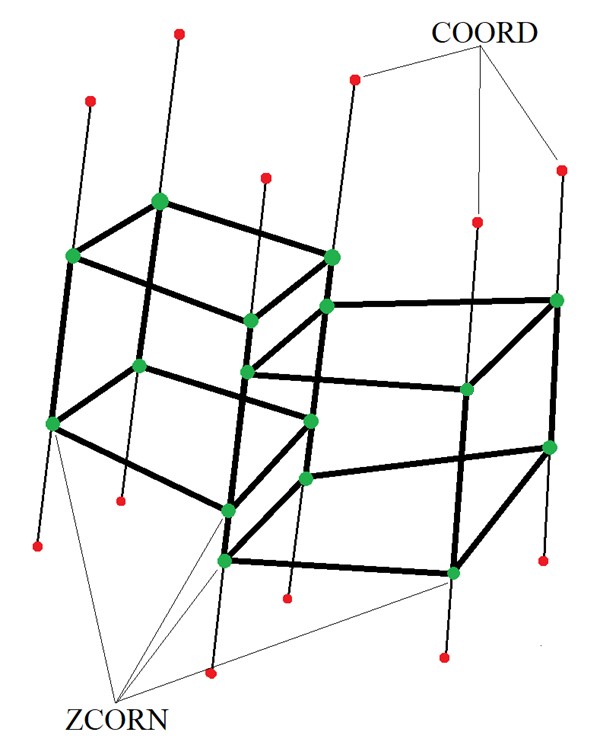
Формат сетки ГУТ достаточно прост – можно бегло ознакомиться с ним в нашей предыдущей статье или на Википедии. Вместо того, чтобы тратить на это много времени (мы же обещали, что справимся за час), перейдём сразу к реализации рендерера, а с форматом разберёмся по ходу.
Требования к рендереру ГУТ
Рендерер угловой геометрии должен отвечать нескольким требованиям, в субъективном порядке убывания важности:
поддержка пикинга: определение координат и индексов ячейки под курсором при нажатии/наведении мыши. Это ключевое требование для интерактивной работы с моделями;
способность отображать сетки размером 1003 ~ 10003 ячеек на типовых конфигурациях компьютеров;
приемлемое время начальной загрузки данных, в идеале не больше 10-30 сек;
отображение любых входных ГУТ без долгих предрасчётов;
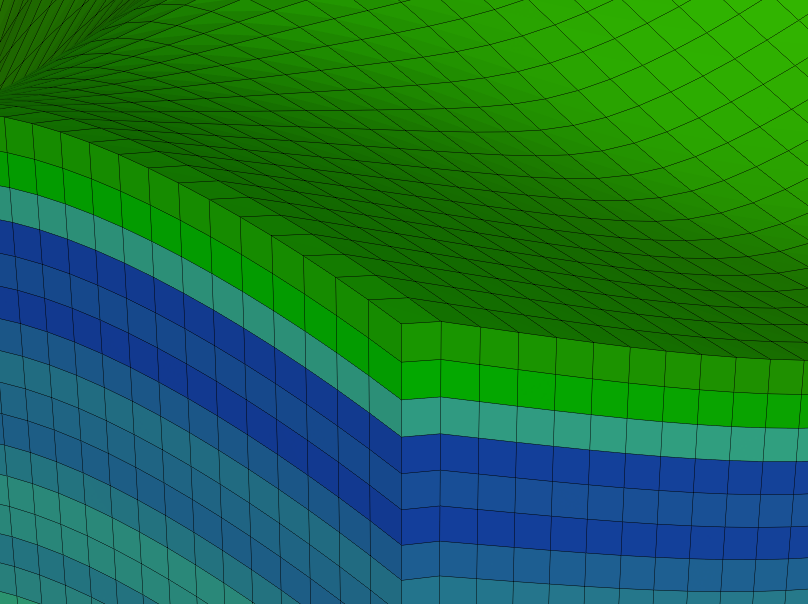
закраска ячеек по палитре с поддержкой wireframe-границ ячеек, иначе на экране ячейки сливаются друг с другом (см. рис. 2);
адекватная частота кадров: от 60 до 20 FPS.
Из этих требований вытекают ограничения на возможность применения сложных алгоритмов отсечения в предрасчёте, а также сложных моделей освещения вроде PBR (Physically-Based Rendering). Вопросы красивости визуализации никого не волнуют; главное, чтобы пользователь быстро получал интересующую его информацию об отображаемой модели.
Чтобы читателю было проще представить, насколько огромными могут быть сетки угловой геометрии, сравним возможные размеры сетки с тем же Майнкрафтом версии 1.16.4 (на момент написания статьи). На стандартных настройках графики в область видимости в этой игре входит чуть более 11 миллионов блоков или примерно 2223. На максимальных настройках это число составляет уже более 71 миллионов блоков или примерно 4143.
В случае геологических моделей, размеры сетки ГУТ порядка 2503 ячеек считаются небольшими; размеры порядка 5003 – 10003 ячеек считаются большими, а размеры порядка 10003 – 20003 ячеек считаются огромными и непрактичными для повседневной работы даже на мощных рабочих станциях.
Утилиты
Все входные данные угловой геометрии будем считать плотно упакованными трёхмерными массивами в порядке C (row-major). Для удобства заведём простой класс span3d упрощающий работу с трёхмерными массивами. Этот класс не владеет переданным ему массивом, а просто ссылается на него, как и std::span Вместо этого класса можно использовать любую подобную обёртку над многомерными массивами, например std::mdspan (если он будет добавлен в C++ в будущем стандарте), или xtensor.
template<typename T>
struct span3d {
T* const data;
const uint32_t ni;
const uint32_t nj;
const uint32_t nk;
span3d(T* _data, uint32_t _ni, uint32_t _nj, uint32_t _nk)
: data(_data), ni(_ni), nj(_nj), nk(_nk) { }
T at(size_t x, size_t y, size_t z) const {
return data[x * nj * nk + y * nk + z];
}
T& at(size_t x, size_t y, size_t z) {
return data[x * nj * nk + y * nk + z];
}
};
Построение ГУТ
Приступим к реализации загрузчика угловой геометрии. Все данные будем хранить в классе CornerPointGrid.
struct CornerPointGrid
{
CornerPointGrid(uint32_t ni, uint32_t nj, uint32_t nk,
const float* coord, const float *zcorn, const float* property, const uint8_t* mask);
~CornerPointGrid();
void render(GLuint shader,
const Palette& palette,
const mat4& proj_view,
const mat4& model,
vec3 light_direct,
bool primitive_picking);
private:
// входные данные
span3d<const float> _coord;
span3d<const float> _zcorn;
span3d<const float> _property;
span3d<const uint8_t> _mask;
// маска состыкованности граней
std::vector<uint8_t> _joined_mask_data;
span3d<uint8_t> _joined_mask; // ссылается на массив _joined_mask_data;
// объекты OpenGL
GLuint _position_vbo;
GLuint _normal_vbo;
GLuint _cell_index_vbo;
GLuint _texcoord_vbo;
GLuint _property_vbo;
GLuint _indexbuffer;
GLuint _vao;
// тут будут приватные методы ...
};
Конструктор принимает размеры сетки (ni, nj, nk)и все входные массивы: COORD, ZCORN, PROPERTY, MASK. Проверять размеры входных массивов мы, конечно же, не будем.
CornerPointGrid::CornerPointGrid(uint32_t ni, uint32_t nj, uint32_t nk,
const float* coord, const float* zcorn, const float* property, const uint8_t* mask) :
_coord(coord, ni+1, nj+1, 6),
_zcorn(zcorn, ni*2, nj*2, nk*2),
_property(property, ni, nj, nk),
_mask(mask, ni, nj, nk),
_joined_mask_data(ni*nj*nk, 0),
_joined_mask(_joined_mask_data.data(), ni, nj, nk) {
// посчитаем маску состыкованности ячеек
calc_joined_mask(_zcorn, _joined_mask);
// рассчитаем число видимых граней
size_t quad_count = calc_number_of_quads(_mask, _joined_mask);
// создаем вершинные и индексный буферы
_create_vertex_index_buffers();
// рассчитаем вершины и индексы и загрузим их в вершинные/индексные буферы
_gen_vertices_and_indices(quad_count);
// назначаем наши вершинные и индексный буфер в VAO
_setup_vao();
}
Массив COORD имеет размер (ni+1, nj+1, 6). В этом массиве хранится набор из (ni+1, nj+1)условно вертикальных отрезков-пилларов, заданных двумя трёхмерными точками. Для каждой ячейки используются четыре соседние пиллара, поэтому общее число пилларов всегда на единицу больше числа ячеек в каждом направлении сетки.
Каждая ячейка задается восемью глубинами своих угловых вершин (отсюда и название ГУТ), которые хранятся в массиве ZCORN. Поэтому размер этого массива в восемь раз больше размерности сетки: (ni*2, nj*2, nk*2). Мы могли бы хранить все восемь угловых глубин в последней размерности массива, как в случае COORD, но у такой схемы есть преимущество: если итерировать вниз по пиллару, глубины вершин соседних ячеек лежат в памяти друг за другом подряд, что позволяет симуляторам более эффективно использовать кэш во многих расчётах.
Массив PROPERTY содержит значение какого-то свойства в каждой ячейке, например, значение пористости или нефтенасыщенности. Согласно этому значению мы раскрашиваем каждую ячейку в тот или иной цвет палитры.
Массив MASK содержит булево значение активности ячейки. Если ячейка неактивна, она не участвует в расчётах модели, и её мы не рисуем.
Также в конструкторе создаётся массив из байт под маску состыкованности граней.
Маска состыкованности граней
Посмотрим ещё раз на картинку в начале статьи. Мы видим на ней внешние грани ячеек сетки, и не видим внутренние, коих в сетке подавляющее большинство. Очевидно, что если не рисовать внутренние грани, частота кадров значительно увеличится, поэтому нам нужен быстрый способ определить, можно ли отсечь невидимые грани всех ячеек.
Формат ГУТ позволяет описывать сетки, ячейки которых не стыкуются с соседними, в отличие от регулярных сеток. Но это свойство угловой геометрии несколько усложняет проверку видимости граней – недостаточно только лишь знать, активна ли соседняя ячейка. Если соседние грани двух ячеек не состыкованы (другими словами, если хотя бы одна из соответствующих вершин граней не совпадает с вершиной соседней грани), то эти грани должны быть нарисованы, даже если обе ячейки активны.
Мы могли бы выполнять эту проверку прямо при генерации вершин, но есть смысл сохранить результат в отдельный массив как битовую маску состыкованности граней. Наличие маски состыкованности позволяет быстрее переключать маску активности ячеек – не придётся повторно проверять состыкованность граней.
enum JoinedMaskBits : uint8_t {
I_PREV = 1 << 0, I_NEXT = 1 << 1,
J_PREV = 1 << 2, J_NEXT = 1 << 3,
K_PREV = 1 << 4, K_NEXT = 1 << 5
};
static void calc_joined_mask(span3d<const float> zcorn, span3d<uint8_t> joined_mask) {
// с какой точностью сравниваем совпадение граней, ~10 см вполне достаточно.
const float eps = 0.1f;
// для каждой ячейки результирующей маски
for(uint32_t i = 0; i < joined_mask.ni; ++i) {
for(uint32_t j = 0; j < joined_mask.nj; ++j) {
for(uint32_t k = 0; k < joined_mask.nk; ++k) {
// индексы этой ячейки в zcorn
uint32_t iz = i * 2, jz = j * 2, kz = k * 2;
// проверяем, совпадают ли граничные вершины ячеек (i,j,k) и (i+1,j,k) по оси I
if (i + 1 < joined_mask.ni) {
float d = 0.0f;
d += std::abs(zcorn.at(iz+1, jz, kz ) - zcorn.at(iz+2, jz, kz ));
d += std::abs(zcorn.at(iz+1, jz+1, kz ) - zcorn.at(iz+2, jz+1, kz ));
d += std::abs(zcorn.at(iz+1, jz, kz+1) - zcorn.at(iz+2, jz, kz+1));
d += std::abs(zcorn.at(iz+1, jz+1, kz+1) - zcorn.at(iz+2, jz+1, kz+1));
if (d < eps) {
// совпадают - отметим состыкованность, установив биты I_NEXT и I_PREV
joined_mask.at(i, j, k) |= I_NEXT;
joined_mask.at(i+1, j, k) |= I_PREV;
}
}
// проверяем, совпадают ли граничные вершины ячеек (i,j,k) и (i,j+1,k) по оси J
if (j + 1 < joined_mask.nj) {
float d = 0.0f;
d += std::abs(zcorn.at(iz, jz+1, kz ) - zcorn.at(iz, jz+2, kz ));
d += std::abs(zcorn.at(iz+1, jz+1, kz ) - zcorn.at(iz+1, jz+2, kz ));
d += std::abs(zcorn.at(iz, jz+1, kz+1) - zcorn.at(iz, jz+2, kz+1));
d += std::abs(zcorn.at(iz+1, jz+1, kz+1) - zcorn.at(iz+1, jz+2, kz+1));
if (d < eps) {
// совпадают - отметим состыкованность, установив биты J_NEXT и J_PREV
joined_mask.at(i, j, k) |= J_NEXT;
joined_mask.at(i, j+1, k) |= J_PREV;
}
}
// проверяем, совпадают ли граничные вершины ячеек (i,j,k) и (i,j,k+1) по оси K
if (k + 1 < joined_mask.nk) {
float d = 0.0f;
d += std::abs(zcorn.at(iz, jz, kz+1) - zcorn.at(iz, jz, kz+2));
d += std::abs(zcorn.at(iz+1, jz, kz+1) - zcorn.at(iz+1, jz, kz+2));
d += std::abs(zcorn.at(iz, jz+1, kz+1) - zcorn.at(iz, jz+1, kz+2));
d += std::abs(zcorn.at(iz+1, jz+1, kz+1) - zcorn.at(iz+1, jz+1, kz+2));
if (d < eps) {
// совпадают - отметим состыкованность, установив биты K_NEXT и K_PREV
joined_mask.at(i, j, k) |= K_NEXT;
joined_mask.at(i, j, k+1) |= K_PREV;
}
}
} // for k
} // for j
} // for i
}
Алгоритм генерации маски состыкованности довольно прост: для каждой пары соседних граней двух ячеек проверим, совпадают ли все четыре вершины одной грани с четырьмя вершинами другой грани. Если вершины граней совпадают (с каким-то небольшим epsilon, нам не нужна слишком большая точность), установим в 1 биты этих граней в маске состыкованности граней, которая изначально была заполнена нулями.
Для проверки совпадения вершин граней достаточно сравнивать только глубины вершин из массива ZCORN, поскольку формат ГУТ гарантирует, что вершины соседних граней лежат на одних и тех же пилларах – для одинаковых глубин получатся и одинаковые координаты X и Y. Благодаря этому свойству, маска состыкованности граней генерируется очень быстро, и нет смысла сохранять её на диск – чтение займёт больше времени, чем расчёт маски с нуля.
Расчет числа видимых граней
Этот шаг позволяет нам узнать заранее, сколько памяти выделять под атрибуты вершин. К тому же, не зная требуемый объем памяти, мы не сможем реализовать некоторые оптимизации в будущем.
Алгоритм расчёта числа граней тривиален – интерес представляет лишь функция check_if_quad_culled(), которая использует маску состыкованности граней из предыдущего шага.
static size_t calc_number_of_quads(const span3d<const uint8_t>& mask,
const span3d<uint8_t> joined_mask) {
size_t num_of_quads = 0;
for (uint32_t i = 0; i < mask.ni; ++i)
for (uint32_t j = 0; j < mask.nj; ++j)
for (uint32_t k = 0; k < mask.nk; ++k)
// если ячейка активна
if (mask.at(i, j, k)){
// для каждого возможного полигона
for (uint32_t qi = 0; qi < 6; ++qi){
// определим, нужно ли его создавать
if (!check_if_quad_culled(mask, joined_mask, i, j, k, qi))
// и если нужно, то увеличим счетчик
num_of_quads++;
}
}
return num_of_quads;
}
// Для каждой грани бит, показывающий стыкованность с соседней ячейкой
static const std::array<JoinedMaskBits, 6> cell_quads_joined_mask_bits = {
// то есть ячейка является соседней по оси x, y или z
JoinedMaskBits::J_PREV,
JoinedMaskBits::I_NEXT,
JoinedMaskBits::J_NEXT,
JoinedMaskBits::I_PREV,
JoinedMaskBits::K_PREV,
JoinedMaskBits::K_NEXT,
};
// Для каждой грани индексы соседней ячейки со стороны этой грани
static const std::array<std::array<int, 3>, 6> cell_quads_neighbors = {
// прибавим их к координатам (i,j,k) ячейки - получим координаты соседней ячейки
std::array<int, 3>{ 0, -1, 0},
std::array<int, 3>{ 1, 0, 0},
std::array<int, 3>{ 0, 1, 0},
std::array<int, 3>{-1, 0, 0},
std::array<int, 3>{ 0, 0, -1},
std::array<int, 3>{ 0, 0, 1},
};
static bool check_if_quad_culled(const span3d<const uint8_t>& mask,
const span3d<uint8_t>& joined_mask,
uint32_t i, uint32_t j, uint32_t k, uint32_t qi) {
// грань создавать нужно, если она не состыкована с соседней
if (!(joined_mask.at(i, j, k) & cell_quads_joined_mask_bits[qi]))
return false;
// или если соседняя ячейка не отображается
// (выход за границы не проверяем, т.к. по границе joined_mask == 0)
if (!mask.at(i + cell_quads_neighbors[qi][0],
j + cell_quads_neighbors[qi][1],
k + cell_quads_neighbors[qi][2]))
return false;
// обе проверки не прошли, значит грань можно отсечь
return true;
}
В функции check_if_quad_culled()выполняется две проверки:
состыкована ли эта грань с гранью соседней ячейки – для этого проверяем нужный бит маски операцией побитового И;
активна ли соседняя ячейка – если нет, то грань придётся нарисовать.
Для большинства ГУТ, применяемых в моделировании, эта функция отсекает подавляющее большинство внутренних граней. Это, в свою очередь, позволяет отображать сетки большего размера на одном и том же компьютере.
Генерация атрибутов вершин
После расчёта числа видимых ячеек приступим к главному, ради чего мы здесь собрались. Cначала создадим вершинные буферы, которые мы уже видели в начале статьи.
void CornerPointGrid::_create_vertex_index_buffers() {
// вершинные буферы
glCreateBuffers(1, &_positions_vbo);
glCreateBuffers(1, &_normals_vbo);
glCreateBuffers(1, &_cell_indices_vbo);
glCreateBuffers(1, &_texcoords_vbo);
glCreateBuffers(1, &_values_vbo);
// индексный буфер
glCreateBuffers(1, &_indexbuffer);
}
Пока не будем сразу же выделять память в этих буферах – мы сделаем это в следующей статье в рамках оптимизации. Для простоты, здесь атрибуты будем генерировать в промежуточные массивы в оперативной памяти.
// Индексы вершин, формирующие грани ячейки.
// 6-------7
// /| / |
// 4------5 | k j
// | 2----|--3 |/
// |/ | / 0-i
// 0------1
static const std::array<std::array<uint32_t, 4>, 6> cell_quads = {
std::array<uint32_t, 4>{0, 1, 5, 4},
std::array<uint32_t, 4>{1, 3, 7, 5},
std::array<uint32_t, 4>{3, 2, 6, 7},
std::array<uint32_t, 4>{2, 0, 4, 6},
std::array<uint32_t, 4>{3, 1, 0, 2},
std::array<uint32_t, 4>{4, 5, 7, 6},
};
static vec3 calc_normal(vec3 v1, vec3 v2){
vec3 normal = cross(v1, v2);
return normalize(normal);
}
// Как для грани сформировать два треугольника
static const std::array<uint32_t, 6> quad_to_triangles = {
0, 1, 2, 0, 2, 3
};
void CornerPointGrid::_gen_vertices_and_indices(size_t quad_count) {
const size_t vertex_count = quad_count * 4;
std::vector<float> a_position, a_index, a_property, a_normal, a_texcoord;
// для каждой вершины 3 координаты (x, y и z)
a_position.reserve(3 * vertex_count);
// + три индекса
a_index.reserve(3 * vertex_count);
// + значение свойства ячейки
a_property.reserve(vertex_count);
// + три компоненты нормали
a_normal.reserve(3 * vertex_count);
// + две текстурные координаты (расстояние от вершин до противолежащих сторон)
a_texcoord.reserve(2 * vertex_count);
// …
Каждая грань состоит из двух треугольников, заданных на 4 вершинах. У вершин есть 5 атрибутов:
координаты вершины;
нормаль грани;
индексы ячейки – нужны для пикинга;
текстурные координаты – для рисования границ ячеек;
значение свойства в этой ячейке.
// …
// буфер, куда записываются вершины ячейки
std::array<vec3, 8> cell_vertices;
// для каждой рассматриваемой ячейки
for (uint32_t i = 0; i < _property.ni; ++i) {
for (uint32_t j = 0; j < _property.nj; ++j) {
for (uint32_t k = 0; k < _property.nk; ++k) {
// если ячейка активна — должна быть нарисована
if (_mask.at(i, j, k)){
// рассчитаем 8 вершин, соответствующих ячейке
get_cell_vertices(_coord, _zcorn, i, j, k, cell_vertices);
// …
Как обычно, пройдёмся по всем ячейкам и проверим, активна ли текущая ячейка по маске. Для каждой активной ячейки запишем в буфер трёхмерные координаты всех её восьми угловых вершин с помощью функции get_cell_vertices()
// 6-------7
// /| / |
// 4------5 | k j
// | 2----|--3 |/
// |/ | / 0-i
// 0------1
// Эти массивы определяют отступы для получения каждой из 8-ми вершин
// ячейки по осям x, y, z, если рассматривать только одну ячейку.
static const std::array<uint32_t, 8> cell_vertices_offset_x = {
0, 1, 0, 1, 0, 1, 0, 1
};
static const std::array<uint32_t, 8> cell_vertices_offset_y = {
0, 0, 1, 1, 0, 0, 1, 1
};
static const std::array<uint32_t, 8> cell_vertices_offset_z = {
0, 0, 0, 0, 1, 1, 1, 1
};
// Получаем все 8 вершин, соответствующих ячейке (i, j, k).
static void get_cell_vertices(const span3d<const float>& coord,
const span3d<const float>& zcorn,
uint32_t i, uint32_t j, uint32_t k,
std::array<vec3, 8>& vertices)
{
// для каждой вершины
for (int vi = 0; vi < 8; ++vi) {
// получим индексы пиллара по индексам ячейки
uint32_t pillar_index_i = i + cell_vertices_offset_x[vi];
uint32_t pillar_index_j = j + cell_vertices_offset_y[vi];
// p1 - первая точка пиллара
float p1_x = coord.at(pillar_index_i, pillar_index_j, 0);
float p1_y = coord.at(pillar_index_i, pillar_index_j, 1);
float p1_z = coord.at(pillar_index_i, pillar_index_j, 2);
// p2 - вторая точка пиллара
float p2_x = coord.at(pillar_index_i, pillar_index_j, 3);
float p2_y = coord.at(pillar_index_i, pillar_index_j, 4);
float p2_z = coord.at(pillar_index_i, pillar_index_j, 5);
float z = zcorn.at(2 * i + cell_vertices_offset_x[vi],
2 * j + cell_vertices_offset_y[vi],
2 * k + cell_vertices_offset_z[vi]);
// значение Z для ячейки у нас есть, а X и Y нет,
// зато известно, что (x,y,z) лежит на линии пиллара p1-p2
float t = (z - p1_z) / (p2_z - p1_z);
float x = p1_x + (p2_x - p1_x) * t;
float y = p1_y + (p2_y - p1_y) * t;
vertices[vi].x = x;
vertices[vi].y = y;
vertices[vi].z = z;
}
}
Расчёт трёхмерных координат вершин ячеек довольно прост: зная координаты двух точек пиллара, находим X и Y вершины ячейки с помощью линейной интерполяции по известной глубине ячейки Z, которую мы считываем из массива ZCORN.
Вернёмся к коду генерации атрибутов вершин:
// …
// рассчитаем 8 вершин, соответствующих ячейке
get_cell_vertices(_coord, _zcorn, i, j, k, cell_vertices);
// из вершин формируем грани
for (int qi = 0; qi < 6; ++qi) {
// определим, нужно ли создавать грань
if (!check_if_quad_culled(_mask, _joined_mask, i, j, k, qi)){
// 4 индекса вершин грани
const std::array<uint32_t, 4>& quad = cell_quads[qi];
// посчитаем нормаль грани
vec3 normal = calc_normal(
cell_vertices[quad[0]] - cell_vertices[quad[1]],
cell_vertices[quad[2]] - cell_vertices[quad[1]]);
// …
После проверки, видима ли грань, посчитаем её нормаль и приступим к генерации атрибутов вершин:
// …
// для каждой вершины в полигоне
for (int vii = 0; vii < 4; ++vii){
// координаты очередной вершины
const vec3& v = cell_vertices[quad[vii]];
// записываем атрибуты вершины
a_position.insert(a_position.end(), {v.x, v.y, v.z});
a_index.insert(a_index.end(), {(float)i, (float)j, (float)k});
a_property.push_back(_property.at(i, j, k));
a_normal.insert(a_normal.end(), {normal.x, normal.y, normal.z});
vec2 texcoords = quad_vertices_texcoords[vii];
a_texcoord.insert(a_texcoord.end(), {texcoords.x, texcoords.y});
} // for vii
}
} // for qi
}
} // for k
} // for j
} // for i
Получив очередную вершину, запишем в массивы атрибутов её координаты, нормаль, индексы ячейки, значение ячейки, и текстурные координаты, заданные следующим массивом:
// Для того, чтобы рисовать сетку на границах ячеек,
// надо знать насколько близко расположен пиксель к границе.
// Тут перечислены текстурные координаты для каждой вершины грани,
// которые позволяют получить расстояние до границы
// (если один из компонентов равен нулю, то это и есть граница).
static const std::array<vec2, 4> quad_vertices_texcoords = {
vec2(1, 0),
vec2(0, 0),
vec2(0, 1),
vec2(0, 0),
};
После того, как все атрибуты вершин заполнены, остаётся только загрузить массивы атрибутов в VBO (Vertex Buffer Object):
glNamedBufferStorage(_position_vbo, a_position.size() * sizeof (float), a_position.data(), 0);
glNamedBufferStorage(_normal_vbo, a_normal.size() * sizeof (float), a_normal.data(), 0);
glNamedBufferStorage(_cell_index_vbo, a_index.size() * sizeof (float), a_index.data(), 0);
glNamedBufferStorage(_texcoord_vbo, a_texcoord.size() * sizeof (float), a_texcoord.data(), 0);
glNamedBufferStorage(_property_vbo, a_property.size() * sizeof (float), a_property.data(), 0);И можно приступать к генерации индексов, формирующих по два треугольника для каждой грани:
// на каждую грань два треугольника
size_t indices_count = quad_count * 6;
std::vector<uint32_t> indices;
indices.reserve(indices_count);
for (size_t i = 0; i < quad_count; ++i)
for (uint32_t j = 0; j < 6; ++j)
// индекс очередной вершины при составлении треугольников
indices.push_back(static_cast<uint32_t>(i * 4 + quad_to_triangles[j]));
glNamedBufferStorage(_indexbuffer, indices.size() * sizeof (uint32_t), indices.data(), 0);
// запомним получившееся число индексов, понадобится в glDrawElements()
_triangle_count = indices.size();
} // конец метода _gen_vertices_and_indices
На этом с генерацией вершин и индексов мы закончили, так что дело за малым: назначить атрибуты в VAO (Vertex Array Object) и начать рендерить ГУТ с помощью шейдеров.
void CornerPointGrid::_setup_vao() {
glCreateVertexArrays(1, &_vao);
// назначаем индексный буфер в VAO
glVertexArrayElementBuffer(_vao, _indexbuffer);
// назначаем все атрибуты в VAO:
// position
glVertexArrayVertexBuffer(_vao, 0, _position_vbo, 0, sizeof (float) * 3);
glVertexArrayAttribBinding(_vao, 0, 0);
glVertexArrayAttribFormat(_vao, 0, 3, GL_FLOAT, GL_FALSE, 0);
glEnableVertexArrayAttrib(_vao, 0);
// normal
glVertexArrayVertexBuffer(_vao, 1, _normal_vbo, 0, sizeof (float) * 3);
glVertexArrayAttribBinding(_vao, 1, 1);
glVertexArrayAttribFormat(_vao, 1, 3, GL_FLOAT, GL_FALSE, 0);
glEnableVertexArrayAttrib(_vao, 1);
// cell index
glVertexArrayVertexBuffer(_vao, 2, _cell_index_vbo, 0, sizeof (float) * 3);
glVertexArrayAttribBinding(_vao, 2, 2);
glVertexArrayAttribFormat(_vao, 2, 3, GL_FLOAT, GL_FALSE, 0);
glEnableVertexArrayAttrib(_vao, 2);
// texcoord
glVertexArrayVertexBuffer(_vao, 3, _texcoord_vbo, 0, sizeof (float) * 2);
glVertexArrayAttribBinding(_vao, 3, 3);
glVertexArrayAttribFormat(_vao, 3, 2, GL_FLOAT, GL_FALSE, 0);
glEnableVertexArrayAttrib(_vao, 3);
// property
glVertexArrayVertexBuffer(_vao, 4, _property_vbo, 0, sizeof (float));
glVertexArrayAttribBinding(_vao, 4, 4);
glVertexArrayAttribFormat(_vao, 4, 1, GL_FLOAT, GL_FALSE, 0);
glEnableVertexArrayAttrib(_vao, 4);
}
struct Palette {
float min_value;
float max_value;
GLuint texture;
};
void CornerPointGrid::render(GLuint shader,
const Palette& palette,
const mat4& proj_view,
const mat4& model,
vec3 light_direct,
bool primitive_picking)
{
// подразумеваем, что вызывающий код настроил фреймбуфер,
// включил тест и запись глубины, включил backface culling
glUseProgram(shader);
// матрица MVP
mat4 mvp = proj_view * model;
glProgramUniformMatrix4fv(shader, glGetUniformLocation(shader, "u_mvp"), 1, GL_FALSE, &mvp[0][0]);
// матрица поворота нормалей
mat3 normal_mat = transpose(inverse(mat3{model}));
glProgramUniformMatrix3fv(shader, glGetUniformLocation(shader, "u_normal_mat"), 1, GL_FALSE, &normal_mat[0][0]);
// направление света и режим пикинга
glProgramUniform3fv(shader, glGetUniformLocation(shader, "u_light_direct"), 1, &light_direct[0]);
glProgramUniform1i(shader, glGetUniformLocation(shader, "u_primitive_picking"), primitive_picking);
// палитра
glBindTextureUnit(0, palette.texture);
// подразумеваем, что для текстуры палитры были заданы опции GL_TEXTURE_WRAP_S == GL_CLAMP_TO_EDGE
// и GL_TEXTURE_{MIN,MAX}_FILTER == GL_LINEAR
glProgramUniform2f(shader, glGetUniformLocation(shader, "u_value_range"), palette.min_value, palette.max_value);
// рисуем
glBindVertexArray(_vao);
glDrawElements(GL_TRIANGLES, _triangle_count, GL_UNSIGNED_INT, nullptr);
// сбрасываем все состояние на дефолтное
glBindVertexArray(0);
glBindTextureUnit(0, 0);
glUseProgram(0);
}
Для задания формата атрибутов в OpenGL применяется объект Vertex Array Object. Сам по себе VAO ничего не хранит, а только лишь ссылается на вершинные и индексный буферы и задаёт отступы и размеры, согласно которым вершинный шейдер считывает очередной атрибут из видеопамяти.
В функции render() мы передаём в шейдер uniform-переменные, задающие параметры рендеринга:
матрицу MVP-преобразования (Model-View-Projection);
матрицу поворота нормалей;
диапазон значений в палитре;
направление источника света;
режим пикинга.
Также назначаем текстуру палитры в юнит под номером 0.
Остаётся только забиндить VAO и вызвать glDrawElements() с запомненным ранее числом индексов.
Шейдеры
Не будем рассматривать процесс компиляции и линковки шейдера, поскольку он часто специфичен для каждого движка и не представляет особого интереса в этой статье. Приведём сразу код вершинного и фрагментного шейдеров.
Вершинный шейдер:
#version 440
// позиция (см. индексы атрибутов в _setup_vao)
layout(location=0) in vec3 a_pos;
// нормаль
layout(location=1) in vec3 a_normal;
// индекс ячейки
layout(location=2) in vec3 a_ind;
// текстурные координаты
layout(location=3) in vec2 a_texcoord;
// значение в ячейке, по которому можно получить цвет
layout(location=4) in float a_property;
// текстура с палитрой
layout(binding=0) uniform sampler1D palette_tex;
// матрицы MVP-преобразования
layout(location=0) uniform mat4 u_mvp;
// матрица поворота нормалей
layout(location=1) uniform mat3 u_normal_mat;
// какому диапазону значений соответствует текстура палитры
layout(location=2) uniform vec2 u_value_range;
// включен ли пикинг индексов ячейки
layout(location=3) uniform bool u_primitive_picking;
// вектор направления света
layout(location=4) uniform vec3 u_light_direct;
layout(location=0) out INTERFACE {
// цвет вершины
vec4 color;
// текстурные координаты для расчета границ ячеек
vec2 texcoord;
} vs_out;
void main() {
// MVP-преобразование координат
gl_Position = u_mvp * vec4(a_pos, 1);
// передаем текстурные координаты в фрагментный шейдер
vs_out.texcoord = a_texcoord;
// если делаем пикинг индексов ячеек, вместо цвета передаем во фрагментный шейдер индексы ячейки
if (u_primitive_picking) {
vs_out.color = vec4(a_ind.x, a_ind.y, a_ind.z, 1);
return;
}
// приводим значение ячейки к диапазону палитры
float normalized_value = (a_property - u_value_range.x) / (u_value_range.y - u_value_range.x);
// получим цвет ячейки по текстуре палитры
vec4 cell_color = texture(palette_tex, normalized_value);
// рассчитываем повернутую нормаль
vec3 normal = normalize(u_normal_mat * a_normal);
// косинус угла между нормалью и направлением освещения
float NdotL = max(0, dot(normal, u_light_direct));
// освещение по Фонгу
const float ka = 0.1, kd = 0.7;
vs_out.color = vec4((ka + NdotL * kd) * cell_color.rgb, cell_color.a);
}
В вершинном шейдере, как обычно, проводим MVP-преобразование вершины, после чего передаём нужные данные во фрагментный шейдер. Освещение также посчитаем в вершинном шейдере – так немного быстрее.
Остановимся на пикинге индексов, о котором уже упоминалось несколько раз. Пользователям нужно не просто видеть ГУТ, но и совершать с ней какие-то манипуляции, например, посмотреть, какое значение в ячейке под курсором, отредактировать его. Для этого 3D-движок должен предоставить приложению доступ к индексам ячейки, на которую нажал или навёл мышь пользователь.
Традиционно, пикинг выполняется трассировкой луча в точку, куда нажал пользователь, но нам такое решение не подходит: пришлось бы хранить в оперативной памяти все трёхмерные вершины, не говоря уж о том, что без применения BVН (Bounding Volume Hierarchy) или другой иерархической структуры скорость такого решения далека от оптимальной.
Поэтому мы пошли более простым путём: в атрибуты вершин сохранили индексы ячейки и при запросе пикинга рендерим всю ГУТ в отдельный фреймбуфер размером 1x1 с установленным флагом u_primitive_picking. В этом случае вместо цвета во фреймбуфер попадают индексы ячейки, которые нетрудно выгрузить в оперативную память и передать в приложение. Этот способ пикинга работает довольно быстро, поскольку подавляющее большинство треугольников оказывается за границами вьюпорта и отсекается до растеризации.
Фрагментный шейдер:
#version 440
// включен ли пикинг индексов ячейки
layout(location=3) uniform bool u_primitive_picking;
layout(location = 0) in INTERFACE {
// цвет вершины
vec4 color;
// текстурные координаты для расчета границ ячеек
vec2 texcoord;
} fs_in;
layout(location=0) out vec4 FragColor;
// цвет фрагмента с учетом необходимости рисовать границы ячеек
vec3 border_color(vec2 dist, vec3 color)
{
// на сколько изменяется dist (1 - вершина, 0 - противоположная граница)
// при сдвиге на один пиксель в cторону границы
vec2 delta = fwidth(dist);
// высота тругольника, проведенная к рассматриваемой границе
vec2 len = 1.0 / delta;
// расстояние до границы меньше пикселя - только тогда надо рисовать границу,
vec2 edge_factor = smoothstep(0.2, 0.8, len * dist);
// смешиваем цвет с сеткой
return mix(color * 0.25, color, min(edge_factor.x, edge_factor.y));
}
void main()
{
if (u_primitive_picking) {
// в режиме пикинга в фреймбуфер попадают индексы ячейки вместо цвета
FragColor = fs_in.color;
return;
}
// добавляем сетку
vec3 res_color = border_color(fs_in.texcoord, fs_in.color.rgb);
FragColor = vec4(res_color, fs_in.color.a);
}
Во фрагментном шейдере мы принимаем цвет с уже рассчитанным освещением из вершинного шейдера и добавляем к нему wireframe-закраску – более тёмный цвет на границах ячеек. Этот способ наложения границ ячеек практически не влияет на частоту кадров.

Заключение
В этой статье мы рассмотрели простейший рендерер угловой геометрии, который, тем не менее, предоставляет пользователям все необходимые возможности. Пока что он не отличается особым быстродействием и требует много памяти – заявленный в заголовке миллиард ячеек не потянет. Во второй части статьи мы займёмся оптимизацией генерации ГУТ и уменьшим требуемый объём памяти, проведём сравнение с текущей версией нашего рендерера и другими движками в коммерческом софте. Спойлер: потребление видеопамяти сократится почти в четыре раза!
На этом первая часть статьи о рендеринге угловой геометрии окончена. Надеемся, что она оказалась интересной и полезной. В комментариях ждём ваших вопросов, будем рады обсудить возможные улучшения рендерера!