Есть ветхозаветная легенда о том, как люди в древнем городе Вавилон начали строить башню, но Всевышний перемешал им языки, и башня достроена не была. Еще бы, ведь башню строили сотни маленьких групп, которые в совокупности не понимали друг друга. А не понимая друг друга, невозможно взаимодействовать. Действительно, просто безумие – называть одну и туже вещь, подразумевая её одинаково, разными словами. И удивительного тут ничего нет.
Ветхозаветную легенду можно с легкостью перенести на современные крупные компании, внедряющие современные ИТ-решения. В пример таких компаний, вне всякого сомнения, можно отнести современные российкие банки, которые имеют десятки, а то и сотни бизнес-подразделений, в которых складывается своя субкультура общения, построенная на своих правилах и уникальном стиле делового оборота. Естественно, при формировании ИТ-инфрастурктуры учитывается устоявшийся в коллективе стиль именования бизнес-сущностей. За последние десять лет появилось множество работ на эту тему, например эта [1]. Те, кто сталкивался с аналитикой информационных систем в банках знают, что такое сделать так называемый «маппинг» данных, особенно, если конечные системы делали разные команды аналитиков, разработчиков и заказчиков или вендоров. Как правило, на 60% составление маппинга является уяснением сути и семантики передаваемых данных.
Сейчас модной тенденцией является использования комплекса гибких методологий. Об Agile говорят все. Можно до хрипоты спорить, благо он для бизнеса или вред. Но одна вещь не вызовет ни у кого отторжения. В ходе Agile множество разных команд, как внутри банка, так и со стороны разных вендоров рождает множество ИТ-решений для бизнеса, и часто, не взаимодействуя друг с другом, команды рождают свою устоявшуюся терминологию. И в тот момент, когда интеграция все же происходит, случается та самая, описанная в Ветхом Завете ситуация. Чем она не напоминает вавилонский базар с его тысячами торговцев, лавок, товаров, юродивых, факиров и глотателей огня? И вот, все эти люди, вооруженные разными идеями и разными помыслами, начинают строить Башню.
Мы всегда на выходе спринта имеем набор XSD схем (или примеров JSON сообщений) с полями, которые нужно каким-то образом однозначно сопоставить друг другу. И не важно, где идут споры, может быть это набор «экселевских» таблиц с маппингами, может быть это сотни комментариев в Confluence, может быть это часы конференций в Zoom или Webex, но на наведение порядка в этом «семантическом безумии» тратится время и нервы, а самое главное — деньги.
Конечно же, концепция использования ESB (единой сервисной интеграционной шины банка) и модель глобальных бизнес-объектов, которая используется, например в некоторых европейских банках, где является своеобразной «лингва-франка» между информационными системами, должны позволить уйти от данной ситуации. Но… давайте будем честными, не все компании могут это себе позволить, да и не всем это надо. Ситуация в банковской сфере меняется столь стремительно, что многие заказчики начинают прибегать к концепции взаимодействующих платформ на основе микросервисов, посаженных на какой-нибудь брокер сообщений, типа Kafka. В итоге мы имеем не одну модель данных, а набор моделей данных, созданных под каждый сервис, зачастую отдельной командой. Взаимодействие в рамках данной платформы осуществляется не столь привычными банковским аналитикам XML сообщениями, основанными на использовании жестких XSD схем, разработанных в ходе проектирования командой аналитиков, юристов, представителей бизнеса на века, а более простой и наглядный JSON, пришедший в банковский бек из фронт-разработки вместе с разработчиками, решившими сменить «фронт» на «бек». Не стоит, наверное, говорить, что JSON не может нести жесткую схему. Просто он удобнее для гибких методологий. Его можно поправить, добавив или убрав пару атрибутов. И нет в нем привязки к железобетонным XSD схемам, замешанным на использовании специфических правил записи. JSON проще редактировать и вносить в него изменения. К его изменению проще доступ.
И что мы имеем? Мы имеем набор входных на платформу сообщений, которые надо в соответствии с бизнес-сутью данных передать микросервисам. И вот тут возникает вопрос, а как это сделать побыстрее?
Маппинги данных. Говорим разными словами об одном и том же
В момент интеграции между несколькими ИТ-системами сталкиваются два аналитика. Один со стороны одной системы, другой со стороны соответственно второй системы. В качестве входных данных у них два файла MS Excel, которые нужно, как говорят у нас, «смапить» для реализации разработки адаптера. В этих файлах указаны атрибуты сообщения в одной колонке (как правило в форме JSON path), а в другой — их семантическое описание. Такой документ называется «маппингом». И вот тут начинается самое интересное. Кто сталкивался с маппингами, тот знает что в них могут находится такие описания:
«номер счета физического лица»
«номер счета физика»
«20-значный номер счета физика»
«12-значный счет физического лица»
«номер отделения, в котором открыт счет физического лица»
Это и прочее, являющееся, казалось бы, одним и тем же с точки зрения семантики, едва схоже с точки зрения бизнес-смысла. Ведь банковский счет физического лица может быть разным, например: металлическим счетом, счетом погашения или счетом списания. И все это – “счет физического лица”. Как итог, микросервис при тестировании вернет по запросу, например, вместо металлического счета физического лица совсем не то, что от него ожидали, а скажем, номер счета для погашения кредита.
Вот если бы существовал такой алгоритм, реализованный простым скриптом, написанным на общедоступном языке программирования с огромным количеством удобных библиотек, которые можно легко установить из командной строки через PIP! Такой алгоритм бы подхватывал два файла с расширением xslx и создавал бы третий, в котором уже было бы проведено установление первичного соответствия. Да, вы правы, я о языке Python, который идеально подходит для решения рутинных задач аналитика.
И вот, мы пришли к задаче – провести анализ текстовых данных методами языка Python. Наверное для анализа текстовых данных, есть специализированные библиотеки языка Python. Но, когда ты работаешь в банке и тонко чувствуешь его синергетику, возникает желание придать какую-то количественную и осмысленную оценку точности аналитики. Нужно это, в том числе, и для дальнейшего развития механизма автоматизации работы аналитика. Это непреодолимый соблазн для исследователя – сопоставить рациональное число явлению или, в нашем случае, попаданию в семантическую суть. Как говорил Платон Пифагор: «Все есть число, весь мир есть число». Поэтому и возникла идея — использовать для задания и визуализации точности оценки какой-нибудь из базовых виджетов библиотек PyQt или Tkinter. А для этого, необходимо дать соответствующую числовую характеристику. Тянешь ползунок на экране и регулируешь точность попадания в семантическую цель.
И так, у нас к каждому JSONpath в файле маппинга приложено краткое описание поля, написанное на русском языке кириллическими буквами. И вот тут возникла идея оценить семантическое соответствие, написанного в коментарии в одном файле и в другом, при помощи математического алгоритма, реализованного на языке Python. Да и не просто оценить, а оценить количественно.
На помощь спешит математика. Векторизация комментария в описании полей для JSON. Соединяем лингвистику и аналитическую геометрию
Суть метода состоит в следующем. Предлагается сопоставить каждому комментарию в “экселевском” файле с описанием полей вектор в 33-мерном евклидовом вещественном пространстве при ортонормированном базисе. Почему в 33 мерном? Да очень просто – “33” это количество букв в русском алфавите. Назовем такое пространство «Алфавитным». Что может быть проще. Кстати, метод векторизации текстовых данных известен давно и подробно описан в любом учебнике по машинному обучению, например, тут [2]. В получившемся пространстве мы формируем Декартову систему координат с числовыми осями. По каждой из таких «осей» пространства мы откладываем количество букв в высказывании. Вот тут необхоимо сформировать главную лемму для дальнейших рассуждений: любому высказыванию, выраженному в кириллических буквах, можно однозначно поставить в соответствие вектор в алфавитном 33-мерном евклидовом ортономированном пространстве. Числовыми координатами вектора по соответствующей оси будет количество соответствующей буквы в высказывании. А дальше следует проанализировать семантическое соответствие путем определения разницы между такими векторами по правилам аналитической геометрии. К примеру, алфавитное пространство ABC у нас будет выглядеть следующим образом:
где каждая координата x в соответствующей позиции – это количество соответствующей буквы комментарии к полю в экселевском файле. Например, у нас есть комментарий «Номер счета физического лица». Сопоставим для него вектор, выходящий из начала координат декартовой системы в алфавитном 33 мерном пространстве, выглядеть он будет следующим образом: координата XА — соответствует количеству букв «а». И оно равно двум. XБ – в данном случае будет равно нулю, так как буквы «б» в данном высказывании нет. Тоже самое касается и xВ — буква «в» отсутствует. А вот xИ – будет равен 3, так как буква «и» в комментарии встречается три раза.

Рисунок 1. Проекция алфавитного вектора, соответствующего высказыванию «Номер счета физического лица» на плоскость букв АИ. Количество букв «А»= 2, количество букв «И» =3. Вектор в данной плоскости имеет две координаты по количеству букв – xA=2, xб=3.
Таким образом, если мы строим вектор, берущий начало в нуле (начале координат) декартовой системы, то алфавитный 33-мерный вектор соответствующий высказыванию «Номер счета физического лица», у нас получится следующий:
Теперь, допустим, у нас есть высказывание «Номер счета «физика»» (кто работал в банковской среде, то знает, как тут любят слова «физик» и «юрик») и «Номер счета клиента». Сопоставим им по данному правилу алфавитные вектора и
соответственно:
Теперь найдем разность между векторами в декартовой системе координат алфавитного пространства, находится она соответственно по хорошо известной из аналитической геометрии формуле:
где
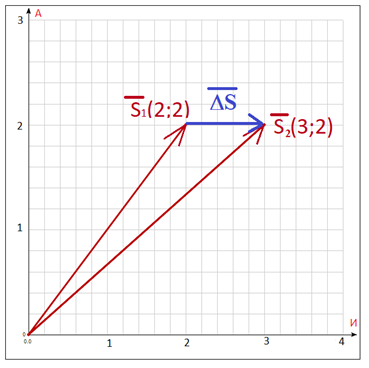
Рисунок 2. Синим цветом показана разность между векторами
Таким образом, вектор, соответствующий разнице между высказываниями «Номер счета физического лица» и «Номер счета физика» будет выглядеть следующим образом:
вектор, соответствующий разнице между высказываниями «Номер счета физического лица» и «Номер счета клиента» будет выглядеть следующим образом:
Далее, вычисляется длина полученных разностных векторов, по формуле:
Если произвести арифметический подсчет, то получится:
Это математически предполагает, что фраза «Номер счета физического лица» по своему смыслу ближе к «Номер счета физика», чем к «Номер счета юридического лица». На это указывают длины разностных векторов. Чем меньше длина, тем ближе по смыслу друг к другу высказывания. Если мы, например, возьмем и сравним высказывания «Номер счета физического лица” и “номер отделения, в котором открыт счет физического лица”, то получим цифру 6.63. Что будет указывать на то что, если первые два высказывания близки по смыслу с исходным (разница векторов 3.32 и 4.00 соответственно), то третье, очевидно, даже будет иметь отличную от него бизнес-суть, несмотря на, казалось бы, видимый одинаковый набор слов.
Можно пойти дальше и попробовать через векторизацию количественно оценить близость комментариев по смыслу. Для этого я предлагаю использовать проекции векторов друг на друга. После чего найти отношение между длинной проекции сравниваемого ветора на длину того, с которым сравнивают. Данное отношение всегда будет меньше, либо равно единице. И соотвественно, если высказывания идентичны друг другу, то проекция сольется с вектором, на который проекцию делают. Чем дальше сравниваемое высказывание будет по смыслу, тем меньше будет составлять проекция. Если его умножить на 100 %, то можно получить степень соответствия векторизованных высказываний в процентах. Таким образом, проекция вектора сравниваемого высказывания
на вектор исходного высказывания
будет находиться по следующей формуле:
Таким образом, степень соответствия

Рисунок 3. Иллюстрация проекции
Именно данный параметр предлагается брать за основу при определении семантического соответствия.
Реализация алгоритма на языке Python. Немного об абрикосе. Как задавать и обращаться с векторами
Алгоритм я назвал Jerdella. Ничего странного, просто я из Ростова-на-Дону.
Атмосфера Нахичеванского базара и бескрайние лотки с абрикосами натолкнули меня на мысли о Вавилоне и смешении языков. Рано или поздно, любой канбан становится похож на Нахичеванский базар в Ростове-на-Дону, где у абрикоса есть, как минимум, три названия. И рано или поздно, выходя на базар в обеденный перерыв за абрикосами, ты начинаешь понимать и по-русски, и по-армянски, и по-украински, и в совершенстве овладеваешь блатной “феней”. Так что, пусть алгоритм будет называться в честь абрикоса.
Еще раз скажу, мне известно, что Python имеет множество библиотек, в том числе и для математической обработки. И есть библиотеки, разработанные специально для методов аналитической геометрии. Например, такой библиотекой является NumPy. Конечно же, ряд читателей зададут вопрос, почему я не использовал NumPy? Отвечаю, во – первых я не считаю данную задачу сложной, тут простые вычисления, а во-вторых все же хотелось прочувствовать реализацию алгоритма и самому все разработанные самолично методы «пощупать руками», чтобы потом нести за результаты полную ответственность. Есть еще одно обстоятельство, почему не NumPy. Это — банковская безопасность. Всем известно, что находясь в сети банка, невозможно устанавливать и обновлять пакеты библиотек через PIP. Поэтому, наша Jerdella будет использовать стандартные пакеты, входящие в поставку PyCharm Community Edition для интерпретатора Python 3.
Итак, язык Python хорош тем, что у него есть возможность реализовывать самые разные структуры данных. И чем нас не устроит список для записи вектора? Список из элементов типа int – это то что нужно для определения вектора в алфавитном пространстве и дальнейших операций с ним.
Нами был написан ряд основополагающих процедур, которые я вкратце опишу ниже.
Как задать вектор?
Вектор я задавал следующей процедурой vector:
def vector(self,a):
vector=[]
abc = ["а", 'б', "в", "г", "д", "е", "ё", "ж", "з", "и", "й", "к", "л", "м", "н", "о", "п", "р", "с", "т",
"у", "ф", "х", "ц", "ч", "ш", "щ", "ъ", "ы", "ь", "э", "ю", "я"]
for char in abc:
count=a.count(char)
vector.append(count)
return(vector)То есть, в цикле for по элементам заранее приготовленного списка abc, я пользовался стандартной операцией по поиску вложений в строку count. После чего, методом append заполнял новый список vector, который и будет являться вектором для дальнейших вычислений.
Как посчитать разницу векторов?
Для этого я создал процедуру delta, принимающую на вход два списка – a и b.
def delta(self, a, b):
delta = []
for char1, char2 in zip(a, b):
d = char1 - char2
delta.append(d)
return (delta)В цикле for путем применения итерации по обоим спискам считалась разница, добавляющаяся на каждом шаге итерации в конец списка delta, который процедура в конечном итоге и возвращала, как вектор.
Как посчитать длину вектора и тем самым оценить разницу?
Для этого я создал процедуру len_delta, которая принимает на вход список, и путем итераций по каждому элементу данного списка (он же является координатой в алфавитном пространстве) по правилу нахождения модуля вектора рассчитывает длину вектора.
def len_delta(self, a):
len = 0
for d in a:
len += d * d
return round(math.sqrt(len), 2)Как посчитать отношение проекции на вектор и тем самым оценить в процентах совпадение?
Для этого была создана процедура simplify, принимающая на вход два списка. В ней я реализовал формулу (6). И тут важный момент – определить какой вектор имеет большую длину. Для большей наглядности оценки совпадения удобнее проецировать меньший вектор на больший.
def simplify(self, a, b):
len1 = 0
len2 = 0
scalar = 0
for x in a: len1 += x * x
for y in b: len2 += y * y
for x, y in zip(a, b): scalar += x * y
if len1 > len2:
return (scalar / len1) * 100
else:
return (scalar / len2) * 100Обсуждение полученных результатов. Покоряем семантическое пространство, структурируя его
Итак, дело было сделано, и Jerdella прекрасно отрабатывала и успешно формировала автоматически маппинги. Но при условии: 1) Когда количество полей, с одной и другой стороны, совпадало. 2) когда поля были описаны подробно в соответствии со своим бизнес-смыслом. Например, данный алгоритм показывал хорошие результаты при интеграции между CRM Siebel и ESB, на котором использовалась модель глобальных бизнес-объектов. В данном случае и со стороны одной системы, и со стороны другой вендоры с глубокой тщательностью, в соответствии с долговременными контрактами, прописывали бизнес-смысл. Было даже пару раз, когда формировали документ автоматически, и не глядя отдавали в разработку. И… все получалось. Казалось бы, можно отправлять аналитиков, делающих маппинги, мести улицы…
Но… на проектах последних 2х лет, завязанных на Agile, с постоянной миграцией команд и кадров, интеграцией банковских платформ по схеме point-to-point, приносящих и уносящих новую семантику проектов, начались проблемы.
Часто спецификой таких проектов является параллельное написание документации. Аналитики не тратят время на глубокую проработку описания полей, а наскоро описывают их, делая упор на разработку схемы сообщения. Часто в описании поля указано 2-3 слова, дающее составление вектора, жестко направленного по ограниченному числу осей в алфавитном пространстве. Например, описанный алгоритм мало чувствителен к соответствию высказываний, состоящих из небольшого числа слов, например: «Номер счета» и «Банковский счет клиента», если в ряду прочих будут высказывания типа «номер отделения», «номер строения», «номер квартиры», то алгоритм векторизации потянется к ним, потому что совпадений по осям больше. Что делать, если у вас с одной стороны приходит 3000 таких вот плохо описанных реквизитов, а с другой готовы принять только 500 и описание также не очень подробное? И как быть с другой возникающей проблемой – несовпадении типов передаваемых данных? Вот тут начинается самое интересное. И возникает вопрос, как кластеризовать и разбить на группы эти не поддающиеся какому-либо описанию 3000 реквизитов?
Тогда у меня возникла идея использовать данный алгоритм и кластеризовать все поля по смыслу. Для этого зададим значение «разничного» вектора или проекции и сгруппируем таким образом те атрибуты, которые пройдут отбор по значениям данных величин. Ведь у нас в руках появляется числовой параметр соответствия одного термина другому. Язык Python позволяет это сделать просто и изящно. У него в арсенале есть так называемые «словари». Ключом такого “словаря” можно сделать сущность делового оборота, которая нас интересует. Назовем её «столбовой сущностью». А значением этого словаря будет являться список, состоящий из словарей, в которых ключом уже будет являтся параметр соответствия, а значением – соответствующий комментарий к полю.
Вот, например вот так:
{'Номер счета физического лица': [{4.69: 'Банковский счет клиента'}, {6.0: 'Фамилия'}, {4.8: 'Номер металлического счета'}, {4.8: 'Номер клиента'}]}.
Эту схему можно также визуализировать в форме графа. Со словарями в языке Python можно много чего делать… Для визуализации и демонстрации результатов мы применяли открытый интернет-проект www.graphonline.ru. Данная платформа позволяет быстро построить граф, записанный через GraphML.

Рисунок 4. Граф взаимосвязи сущности «Номер физического лица». Иллюстрация наличия «орбит семантического соответствия» у сущности.
Если оценивать параметр длины «разностного» вектора, рассчитанный по формуле (3) и нарисовать граф, отнормировав его по весам, то можно увидеть локальные «скученности» терминов, вокруг которых можно провести правильную окружность определенного радиуса. Эту окружность мы в своей работе назвали «орбитой семантического соответствия» или «семантической орбитой». Конечно же, велик соблазн сразу же определить радиус такой орбиты методами статистики. В прочем, это задача мало того, что слишком интересна, но и требует дополнительного осмысления. И может стать темой для дальнейшей работы.
Что это такое и что это дает? Допустим, мы в ходе анализа выделяем для нашего делового оборота множество «столбовых сущностей» или «бизнес-объектов». Задаем точность (параметры (формула 3) и
формула (5)), и прогоняем алгоритм по всем перечным полей. Таким образом, у нас для каждой «столбовой сущности» подтягивается в словарь перечень атрибутов из списков конечных систем с указанием точности совпадения в процентах. Таким образом, появляется нечто наподобие «семантической карты».
Все становится проще, если аналитики договорятся о наборе передаваемых сущностей, то можно проводить поиск по точности совпадения, и таким образом по смыслу. И вот перед глазами аналитиков уже осознаваемый и поддающийся осмыслению список кластеров терминов. И им гораздо легче осознать предметное поле и задачу.

Рисунок 5. Прототип семантической карты, построенной в виде графа взаимосвязи сущностей с указанием параметра соответствия .
Можно аналитикам и не договариваться, а просто запустить данный метод и сравнить каждый атрибут с каждым. Получить для каждой пары параметр соответствия и… кластеризовать, скажем методами кристаллофизики или астрофизики, где механизм кластеризации отработан десятилетиями. И в сущности, какая разница – кристалл сегнетоэлектрика или семантическая карта делового оборота банка? Ну почему нет? Ведь что является кластером в данном случае? Кластер атрибутов — это совокупность наиболее близко лежащих друг к другу в алфавитном пространстве сущностей. Вот сущности соответствующие друг другу на 80%, допустим, кластер. В прочем, определение количественной характеристики для кластеризации это тема для отдельного исследования. И вообще, это уже совсем другая история… но кластеризация бизнес-сущностей и составление семантических карт – это в ближайшем будущем очень перспективная вещь. Особенно, в разрезе машинного обучения.
Когда мы стали получать графы взаимосвязи всех комментарий к полям, мы обнаружили, что кластеризация, действительно, имеет место быть. И самое поразительное, что глядя даже на такую, не сильно структурированную «Вселенную» семантического смысла (рисунок 6), можно наскоро оценить смысл и специфику передаваемых данных. Можно в этой вселенной различить «галактики», «туманности», «скопления», кучкующиеся вокруг какого-то бизнес-смысла. И самое удивительное, что это действительно увеличило скорость анализа в среднем до 30% времени. Визуализация дает возможность быстрее уяснить смысл. А дальше возникла идея проверить, какие изменения в описания позволяют получить более контрастную картину. То есть, не то чтобы создать единое правило формирования описаний, а скорее понять, что должно произойти чтобы произошло полное перемешивание смыслов.

Рисунок 6. «Вселенная» семантического смысла. Пример построенного графа, иллюстрирующего семантическое пространство типичной модели данных.
Вместо заключения. Как определение семантики происходит зачастую на самом деле.
Часто для решения задач по определению семантики применяется «командно-административный» подход. То есть, когда сроки поджимают, чьим-то волевым решением ускоряются темпы аналитики. Почему он плох? Потому что, при таком подходе можно лишить гармонии и синергетики бизнес-процесс.
Мне вспомнилась история. Как-то в одном из полков морской пехоты Северного флота замполит решил организовать хор из матросов. Для чего была выписана музработник, для работы с матросами. И вот замполит подумал: «Долго что-то репетируют». А, меж тем, последнее воскресение июля все ближе. И научиться петь «растаял в далеком тумане Рыбачий» надо бы побыстрее. На вопрос, в чем проблема, музработник сказала, что не удается ей никак разбить пятьдесят матросов по высоте вокала на пять тонов. Тогда замполит сказал – «Не вижу трудностей! На первый-пятый рассчитайсь»…
Аналитики, которые сделают мапинг таким образом, под чьим-то волевым решением, могут упустить тот момент, что «банковский счет физ лица», в зависимости от «конто счета» может быть как «скс счетом», так и «металлическим счетом», а также «счетом погашения кредита или ссуды». И все это могут записать, как «номер счета физического лица». И вот микросервис при запросе депозитных или скс счетов клиента возвращает счета погашения или счет, с которого клиенту выдавали кредит. Итог? Еще один спринт? Очередное последующее «костыльное решение»?
К сожалению, при попытке внедрить нечто наскоро, без предварительной оценки роли участников взаимодействия, особенно, если речь идет о внедрении микросервисов, банк рискует исказить исходный смысл передаваемых данных. И данная статья – это попытка математически провести такую оценку.
Я благодарен следующим авторам за труды, без которых не было бы данной статьи:
[1] Б.Я Шведин. Онтология предприятия: экспириентологический подход. УРСС. 2010.
[2]Б. Бенгфорд, Р. Билбро, Т. Охеда. Прикладной анализ текстовых данных на Python.Машинное обучение и создание приложений естественной обработки языка. – Спб. Питер, 2019, — 368 с.
P.S. Я хотел бы выразить благодарность своим коллегам из компании Accenture — Эльвире Самигулиной, Анаиде Шагинян и Вере Вишняковой за полезные дискуссии относительно данной статьи