О, Боже, четвертая часть! Это выше моих сил! Спокойствие, у меня заканчиваются таблетки, поэтому это последняя статья, и в ней будут разоблачения. Под катом описание процесса подгонки, ушепритягивания, запутывания и манипуляций.
В предыдущих (1, 2, 3) частях мы видели как разные пропорции использовались в геометрии, античном искусстве и современном промышленном дизайне. У нас осталась нераскрытой тема золотого сечения и еще одного корня — √5. Начнем же.
Однажды, люди натолкнулись на идею пропорций. В различных фигурах постоянно встречались одни и те же закономерности. Это впечатляло. Потом кто-то додумался измерить парочку растений, зверюшек и некоторые части тела, которые обычно от посторонних прячут. Закономерности оказались и там. Это впечатляло еще больше.
Терпеть не осталось больше мочи, самые распространенные отношения были объявлены священными. Некоторые видели в них проявление божественного вмешательства. Некоторые — самого бога. А раз священные пропорции так часто встречаются, то можно под них подогнать все что хочешь, сделать из этого символ и стращать паству.
Мистификации и приписки из самых благих намерений встречаются в истории постоянно. Например, переписчики классического труда «Церковная история народа Англов» Беды Достопочтенного приделывали к тексту куски, дабы определенные церковные вопросы выглядели более благоприятно. А 25-28 главы VI книги «Записок о галльской войне» Цезаря по всей видимости не такие уж и Цезаря.
Так же и в символике. Надо чтобы люди чувствовали ее глубинный смысл, а сама форма не так важна. Возьми любую картинку, в ней обязательно да что-нибудь отыщется. Чем древнее, тем лучше. Самый древний у нас Египет, поупражняемся на нем.
Вот схема барельефа из гробницы Петосириса, найденной в 1919 году.

Посидев достаточное время с линейкой и циркулем, в нем можно отыскать и золотое сечение и еще кучу разных отношений (помимо буковок text, остряки, для этого не нужен циркуль).
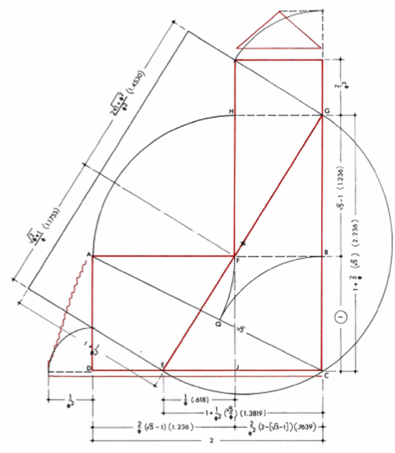
Выглядит достаточно круто, поэтому нет причин не заявить, что Египтяне знали о золотом сечении и специально все так сделали.
Мистифицировать геометрию легко и просто. Сейчас я покажу вам пару приемов. Загляните под кат.
Итак, приемы. Ну во-первых, все эти пропорции настолько древние, что все самые классные построения хорошо описаны. Открыв справочник, мы видим как самым простецким образом забубенить те самые золотые пропорции. Берем квадрат, рисуем впритык такой же и проводим диагональ AC.

С центром O и радиусом OA строим окружность. Продляем линию FE до точки пересечения с окружностью K. Дальше можно повторить фокус с окружностью для стороны AB, но легче провести из К перпендикуляр KH, продлить AB и отметить точку пересечения H.

Вуаля, у нас получился «золотой прямоугольник». Отношение FE к EK такое же, как FK к FE. Что еще более офигенно, KF / FB тоже этому равно. Для краткости Греки назвали это отношение φ (Фи). Оно примерно равно 1.618
Проявляем творческое начало и делаем еще парочку пассов. Соединим углы исходного квадрата и получившегося прямоугольника. Нарисуем по образовавшимся точкам кружочек.
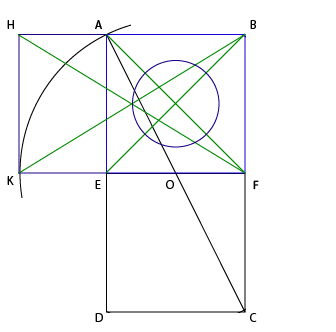
Теперь, для открытия завесы над великой тайной нам нужно найти что-то такое, чтобы вписалось в этот прямоугольник. Вспомнив как нам везло с эпплом, давайте пойдем самым простым путем и сделаем очевидное.

Ура! У нас получилось объявить iPod 4G священным устройством. Совершенно очевидно, что теперь его будут обязательно покупать.
Вот она — польза изучения учебников. Геометрия так долго существует, что ничего не стоит брать справочники, да классические источники, писать книжки и зарабатывать на этом много много профита.

Глядишь, книжку экранизируют с каким-нибудь актером офигевшего от сценария вида, и профита станет еще на порядок больше. Можно компостировать мозг читателя, а можно компостировать мозг читателя тем как можно компостировать мозг читателя — тоже, кстати, прибыльно (ну вы понимаете о чем я, мои начитанные комментаторы). На крайняк, можно поразить современников и заработать кой-какие плюсы разгадав тайны арабской мозаики, связав ее… ну скажем с пчелой.

На самом деле в искусстве разумеется все дело в обычных модульных сетках и направляющих линиях, которые используют художники и дизайнеры для составления композиций. Идея настолько стара, что ее использовали даже самые древние из древних египтян.
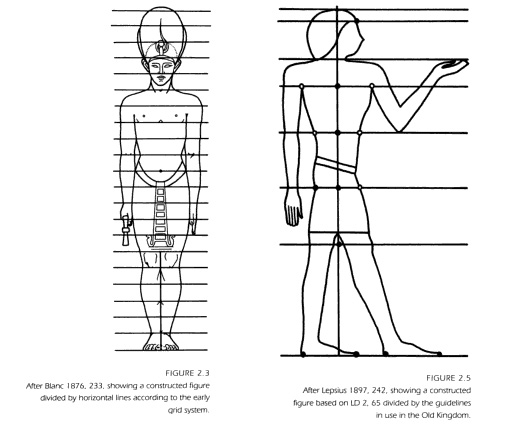
Композиции учат в художественных школах, а тех, кто учит тоже кто-то когда-то учил. Так что никакой мистики. Разве что только самый самый первый учитель что-то там напридумывал. Остальным достаточно взять какую-нибудь сетку и расставить по ней элементы.
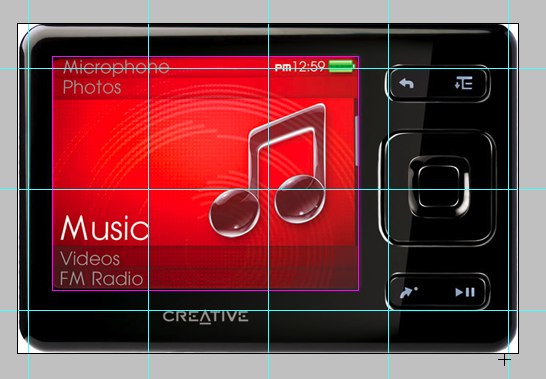
Но полуторное отношение сторон и квадратные модули — это не интересно. Нету тайны. Лучше взять что-нибудь более «сакральное». Скажем, еще одно известное отношение — √5. У плеера Zune как раз такое.

Поглядим в справочник и посмотрим какие могут всплыть закономерности.

Наложим их на плеер. Хм. Ничего похожего пока нет. Попробуем перебрать все варианты.
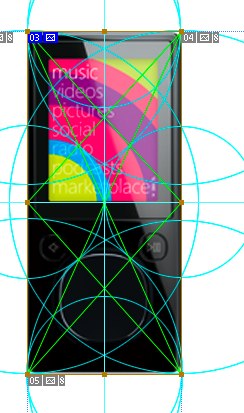
Эммм… Как-то тухло. Интересны разве что касания около центральной кнопки. Тогда будем играть с 4итами. Притащим линейку, померим размеры элементов и попробуем найти делители.

Объясняет саркоидоз и агрессивное поведение… черт, кажется не в то окно пишу. В общем, тут опять унылые квадратики, которыми мало кого запутаешь. Запороли такое хорошее начало.
Придется опять вернуться к айподам. iPod Nano 2G тоже обладает соотношением сторон √5 / 1 Давайте снова посмотрим на схему из справочника и подумаем как прилепить его к чему-нибудь. Ага. Есть сторона √5, которую можно втиснуть в предыдущее построение.

Из точек A, O и C проведем дуги с радиусом AB (так как это у нас 1x, а AC — √5x). Из этих же точек проведем перпендикуляры к AC до пересечения с дугами. Соединим новые пересечения и вот наш айпод уже почти готов.

Ахайлай, махалай, абра-кадабра!
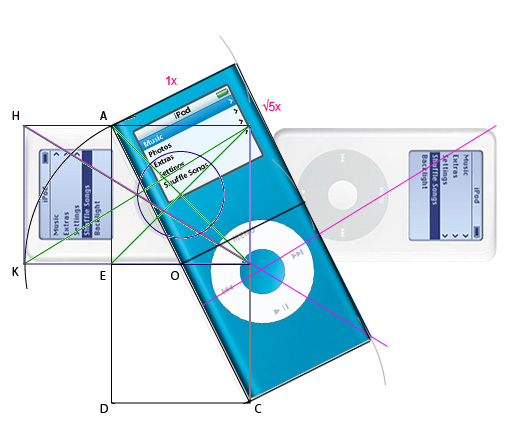
Итак, что же мы узнали?
1. Если хочешь запутать людям голову, всегда надо использовать мистические цифры √2, √3, √5 и φ. С ними всегда будет больше всего «таинственных» совпадений. Есть еще много интересных вещей типа последовательностей Фибоначчи, спиралей, гномических увеличений и всяких хитрых делений. Но чем проще — тем легче всех запутать, правда?
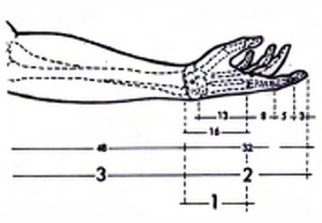

2. Apple совершенно точно промывают людям мозги. Ведь у них есть целый набор юного оккультиста:

3. Из простого квадрата можно сконструировать целый взрыв мозга, религию, алгебру, дихотономию добра и зла.

Каждый увидит здесь что захочет, включая сиськи и Микки-Мауса (еще можно звезду Давида разглядеть, если озаботиться).
Такое вот свойство человека — извращать простые идеи. А ведь вот с чего все начиналось:

В предыдущих (1, 2, 3) частях мы видели как разные пропорции использовались в геометрии, античном искусстве и современном промышленном дизайне. У нас осталась нераскрытой тема золотого сечения и еще одного корня — √5. Начнем же.
Однажды, люди натолкнулись на идею пропорций. В различных фигурах постоянно встречались одни и те же закономерности. Это впечатляло. Потом кто-то додумался измерить парочку растений, зверюшек и некоторые части тела, которые обычно от посторонних прячут. Закономерности оказались и там. Это впечатляло еще больше.
Терпеть не осталось больше мочи, самые распространенные отношения были объявлены священными. Некоторые видели в них проявление божественного вмешательства. Некоторые — самого бога. А раз священные пропорции так часто встречаются, то можно под них подогнать все что хочешь, сделать из этого символ и стращать паству.
Мистификации и приписки из самых благих намерений встречаются в истории постоянно. Например, переписчики классического труда «Церковная история народа Англов» Беды Достопочтенного приделывали к тексту куски, дабы определенные церковные вопросы выглядели более благоприятно. А 25-28 главы VI книги «Записок о галльской войне» Цезаря по всей видимости не такие уж и Цезаря.
Так же и в символике. Надо чтобы люди чувствовали ее глубинный смысл, а сама форма не так важна. Возьми любую картинку, в ней обязательно да что-нибудь отыщется. Чем древнее, тем лучше. Самый древний у нас Египет, поупражняемся на нем.
Вот схема барельефа из гробницы Петосириса, найденной в 1919 году.
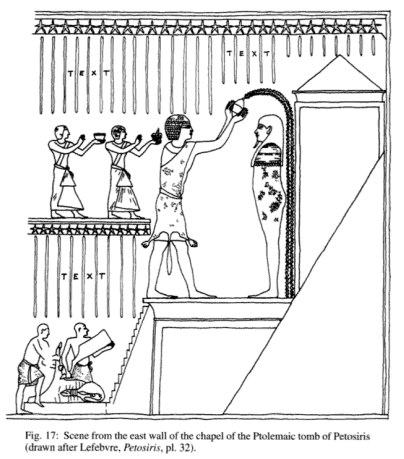
Посидев достаточное время с линейкой и циркулем, в нем можно отыскать и золотое сечение и еще кучу разных отношений (помимо буковок text, остряки, для этого не нужен циркуль).

Выглядит достаточно круто, поэтому нет причин не заявить, что Египтяне знали о золотом сечении и специально все так сделали.
Мистифицировать геометрию легко и просто. Сейчас я покажу вам пару приемов. Загляните под кат.
Итак, приемы. Ну во-первых, все эти пропорции настолько древние, что все самые классные построения хорошо описаны. Открыв справочник, мы видим как самым простецким образом забубенить те самые золотые пропорции. Берем квадрат, рисуем впритык такой же и проводим диагональ AC.

С центром O и радиусом OA строим окружность. Продляем линию FE до точки пересечения с окружностью K. Дальше можно повторить фокус с окружностью для стороны AB, но легче провести из К перпендикуляр KH, продлить AB и отметить точку пересечения H.

Вуаля, у нас получился «золотой прямоугольник». Отношение FE к EK такое же, как FK к FE. Что еще более офигенно, KF / FB тоже этому равно. Для краткости Греки назвали это отношение φ (Фи). Оно примерно равно 1.618
Проявляем творческое начало и делаем еще парочку пассов. Соединим углы исходного квадрата и получившегося прямоугольника. Нарисуем по образовавшимся точкам кружочек.

Теперь, для открытия завесы над великой тайной нам нужно найти что-то такое, чтобы вписалось в этот прямоугольник. Вспомнив как нам везло с эпплом, давайте пойдем самым простым путем и сделаем очевидное.
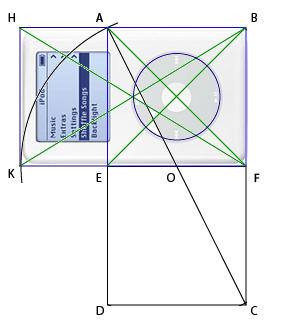
Ура! У нас получилось объявить iPod 4G священным устройством. Совершенно очевидно, что теперь его будут обязательно покупать.
Вот она — польза изучения учебников. Геометрия так долго существует, что ничего не стоит брать справочники, да классические источники, писать книжки и зарабатывать на этом много много профита.
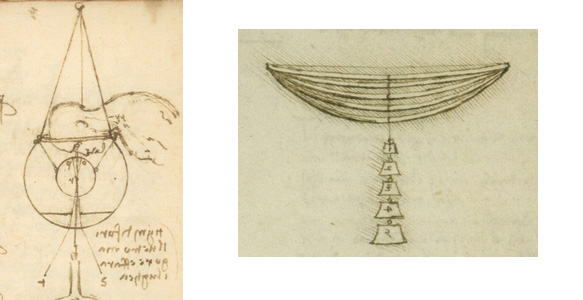
Глядишь, книжку экранизируют с каким-нибудь актером офигевшего от сценария вида, и профита станет еще на порядок больше. Можно компостировать мозг читателя, а можно компостировать мозг читателя тем как можно компостировать мозг читателя — тоже, кстати, прибыльно (ну вы понимаете о чем я, мои начитанные комментаторы). На крайняк, можно поразить современников и заработать кой-какие плюсы разгадав тайны арабской мозаики, связав ее… ну скажем с пчелой.
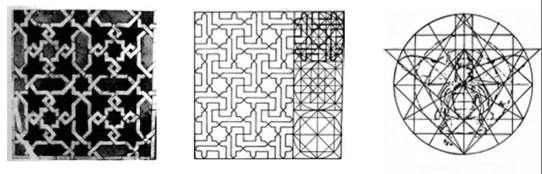
На самом деле в искусстве разумеется все дело в обычных модульных сетках и направляющих линиях, которые используют художники и дизайнеры для составления композиций. Идея настолько стара, что ее использовали даже самые древние из древних египтян.
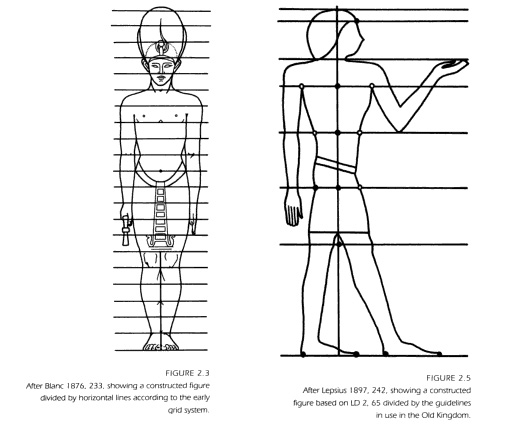
Композиции учат в художественных школах, а тех, кто учит тоже кто-то когда-то учил. Так что никакой мистики. Разве что только самый самый первый учитель что-то там напридумывал. Остальным достаточно взять какую-нибудь сетку и расставить по ней элементы.
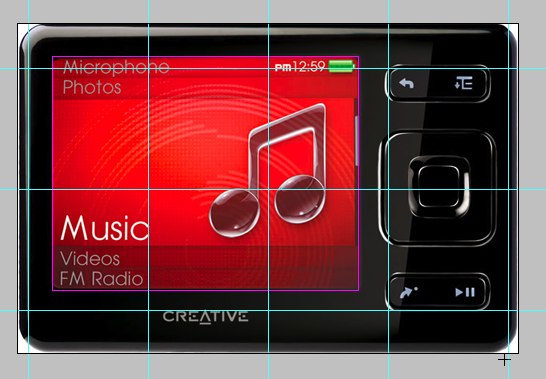
Но полуторное отношение сторон и квадратные модули — это не интересно. Нету тайны. Лучше взять что-нибудь более «сакральное». Скажем, еще одно известное отношение — √5. У плеера Zune как раз такое.

Поглядим в справочник и посмотрим какие могут всплыть закономерности.
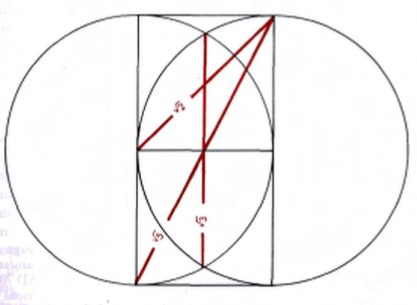
Наложим их на плеер. Хм. Ничего похожего пока нет. Попробуем перебрать все варианты.
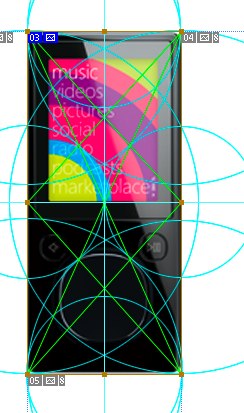
Эммм… Как-то тухло. Интересны разве что касания около центральной кнопки. Тогда будем играть с 4итами. Притащим линейку, померим размеры элементов и попробуем найти делители.
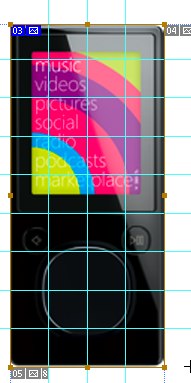
Объясняет саркоидоз и агрессивное поведение… черт, кажется не в то окно пишу. В общем, тут опять унылые квадратики, которыми мало кого запутаешь. Запороли такое хорошее начало.
Придется опять вернуться к айподам. iPod Nano 2G тоже обладает соотношением сторон √5 / 1 Давайте снова посмотрим на схему из справочника и подумаем как прилепить его к чему-нибудь. Ага. Есть сторона √5, которую можно втиснуть в предыдущее построение.

Из точек A, O и C проведем дуги с радиусом AB (так как это у нас 1x, а AC — √5x). Из этих же точек проведем перпендикуляры к AC до пересечения с дугами. Соединим новые пересечения и вот наш айпод уже почти готов.

Ахайлай, махалай, абра-кадабра!

Итак, что же мы узнали?
1. Если хочешь запутать людям голову, всегда надо использовать мистические цифры √2, √3, √5 и φ. С ними всегда будет больше всего «таинственных» совпадений. Есть еще много интересных вещей типа последовательностей Фибоначчи, спиралей, гномических увеличений и всяких хитрых делений. Но чем проще — тем легче всех запутать, правда?


2. Apple совершенно точно промывают людям мозги. Ведь у них есть целый набор юного оккультиста:

3. Из простого квадрата можно сконструировать целый взрыв мозга, религию, алгебру, дихотономию добра и зла.
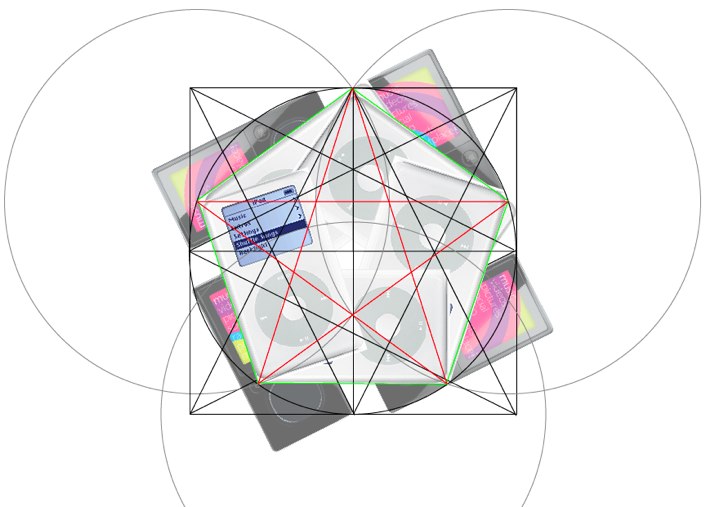
Каждый увидит здесь что захочет, включая сиськи и Микки-Мауса (еще можно звезду Давида разглядеть, если озаботиться).
Такое вот свойство человека — извращать простые идеи. А ведь вот с чего все начиналось:








