Часто наборы данных, с которыми приходится работать, содержат большое количество признаков, число которых может достигать нескольких сотен и даже тысяч. При построении модели машинного обучения не всегда понятно, какие из признаков действительно для неё важны (т.е. имеют связь с целевой переменной), а какие являются избыточными (или шумовыми). Удаление избыточных признаков позволяет лучше понять данные, а также сократить время настройки модели, улучшить её точность и облегчить интерпретируемость. Иногда эта задача и вовсе может быть самой значимой, например, нахождение оптимального набора признаков может помочь расшифровать механизмы, лежащие в основе исследуемой проблемы. Это может быть полезным для разработки различных методик, например, банковского скоринга, поиска фрода или медицинских диагностических тестов. Методы отбора признаков обычно делят на 3 категории: фильтры (filter methods), встроенные методы (embedded methods) и обёртки (wrapper methods). Выбор подходящего метода не всегда очевиден и зависит от задачи и имеющихся данных. Цель настоящего цикла статей - провести краткий обзор некоторых популярных методов отбора признаков с обсуждением их достоинств, недостатков и особенностей реализации. Первая часть посвещена фильтрам и встроенным методам.
1. Методы фильтрации
Методы фильтрации применяются до обучения модели и, как правило, имеют низкую стоимость вычислений. К ним можно отнести визуальный анализ (например, удаление признака, у которого только одно значение, или большинство значений пропущено), оценку признаков с помощью какого-нибудь статистического критерия (дисперсии, корреляции, X2 и др.) и экспертную оценку (удаление признаков, которые не подходят по смыслу, или признаков с некорректными значениями).
Простейшим способом оценки пригодности признаков является разведочный анализ данных (например, с библиотекой pandas-profiling). Эту задачу можно автоматизировать с помощью библиотеки feature-selector, которая отбирает признаки по следующим параметрам:
Количество пропущенных значений (удаляются признаки у которых процент пропущенных значений больше порогового).
Коэффициент корреляции (удаляются признаки, у которых коэффициент корреляции больше порогового).
Вариативность (удаляются признаки, состоящие из одного значения).
Оценка важности признаков с помощью lightgbm (удаляются признаки, имеющие низкую важность в модели lightgbm. Следует применять только если lightgbm имеет хорошую точность.)
Туториал по этой библиотеке находится здесь.
Более сложные методы автоматического отбора признаков реализованы в sklearn. VarianceThreshold отбирает признаки, у которых дисперсия меньше заданного значения. SelectKBest и SelectPercentile оценивают взаимосвязь предикторов с целевой переменной используя статистические тесты, позволяя отобрать соответственно заданное количество и долю наилучших по заданному критерию признаков. В качестве статистических тестов используются F-тест,
и взаимная информация.
F-тест
F-тест оценивает степень линейной зависимости между предикторами и целевой переменной, поэтому он лучше всего подойдёт для линейных моделей. Реализован в sklearn как f_regression и f_classif соответственно для регрессии и классификации.
X2
Этот тест используется в задах классификации и оценивает зависимость между признаками и классами целевой пременной. Описание метода приведено здесьи здесь (для sklearn). Стоит отметить, что этот тип тестов требует неотрицательных и правильно отмасштабированных признаков.
Взаимная информация
Взаимная информация показывает насколько чётко определена целевая переменная если известны значения предиктора (подробнее здесь и здесь). Этот тип тестов считается самым удобным в использовании - он хорошо работает "из коробки" и позволяет находить нелинейные зависимости. Реализован в sklearn как mutual_info_regression и mutual_info_classif соответственно для регрессии и классификации.
2. Встроенные методы
Встроенные методы выполняют отбор признаков во время обучения модели, оптимизируя их набор для достижения лучшей точности. К этим методам можно отнести регуляризацию в линейных моделях (обычно L1) и расчёт важности признаков в алгоритмах с деревьями (который хорошо разобран здесь). Отметим, что для линейных моделей требуется масштабирование и нормализация данных.
Пример
Рассмотрим применение описанных выше методов в реальной задаче – предсказать, зарабатывает ли человек больше $50 тыс. Загрузим библиотеки и данные, для удобства оставив только численные признаки:
age – возраст
fnlwgt (final weight) – примерная оценка количества людей, которое представляет каждая строка данных
educational-num – длительность обучения
capital-gain – прирост капитала
capital-loss – потеря капитала
hours-per-week – количество рабочих часов в неделю
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.feature_selection import GenericUnivariateSelect, mutual_info_classif, SelectFromModel
from sklearn.pipeline import Pipeline
from sklearn.model_selection import StratifiedKFold, GridSearchCV, cross_val_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.preprocessing import PowerTransformer
from sklearn.linear_model import LogisticRegression
# зафиксируем значение генератора случайных чисел для воспроизводимости
SEED = 1
# Функции, которые в дальнейшем понадобятся
def plot_features_scores(model, data, target, column_names, model_type):
'''Функция для визуализации важности признаков'''
model.fit(data, target)
if model_type == 'rf':
(pd.DataFrame(data={'score': model['rf'].feature_importances_},
index=column_names).sort_values(by='score')
.plot(kind='barh', grid=True,
figsize=(6,6), legend=False));
elif model_type == 'lr':
(pd.DataFrame(data={'score': model['lr'].coef_[0]},
index=column_names).sort_values(by='score')
.plot(kind='barh', grid=True,
figsize=(6,6), legend=False));
else:
raise KeyError('Unknown model_type')
def grid_search(model, gs_params):
'''Функция для подбора гиперпараметров с помощью перекрёстной проверки'''
gs = GridSearchCV(estimator=model, param_grid=gs_params, refit=True,
scoring='roc_auc', n_jobs=-1, cv=skf, verbose=0)
gs.fit(X, y)
scores = [gs.cv_results_[f'split{i}_test_score'][gs.best_index_] for i in range(5)]
print('scores = {}, \nmean score = {:.5f} +/- {:.5f} \
\nbest params = {}'.format(scores,
gs.cv_results_['mean_test_score'][gs.best_index_],
gs.cv_results_['std_test_score'][gs.best_index_],
gs.best_params_))
return gs
# загрузим данные
df = pd.read_csv(r'..\adult.data.csv')
# датасет, с которым будем работать
# оставим только численые признаки
X = df.select_dtypes(exclude=['object']).copy()
# преобразуем целевую переменную
y = df['salary'].map({'<=50K':0, '>50K':1}).values
X.head()age | fnlwgt | education-num | capital-gain | capital-loss | hours-per-week | |
|---|---|---|---|---|---|---|
0 | 39 | 77516 | 13 | 2174 | 0 | 40 |
1 | 50 | 83311 | 13 | 0 | 0 | 13 |
2 | 38 | 215646 | 9 | 0 | 0 | 40 |
3 | 53 | 234721 | 7 | 0 | 0 | 40 |
4 | 28 | 338409 | 13 | 0 | 0 | 40 |
X.describe() age | fnlwgt | education-num | capital-gain | capital-loss | hours-per-week | |
|---|---|---|---|---|---|---|
count | 32561.000000 | 3.256100e+04 | 32561.000000 | 32561.000000 | 32561.000000 | 32561.000000 |
mean | 38.581647 | 1.897784e+05 | 10.080679 | 1077.648844 | 87.303830 | 40.437456 |
std | 13.640433 | 1.055500e+05 | 2.572720 | 7385.292085 | 402.960219 | 12.347429 |
min | 17.000000 | 1.228500e+04 | 1.000000 | 0.000000 | 0.000000 | 1.000000 |
25% | 28.000000 | 1.178270e+05 | 9.000000 | 0.000000 | 0.000000 | 40.000000 |
50% | 37.000000 | 1.783560e+05 | 10.000000 | 0.000000 | 0.000000 | 40.000000 |
75% | 48.000000 | 2.370510e+05 | 12.000000 | 0.000000 | 0.000000 | 45.000000 |
max | 90.000000 | 1.484705e+06 | 16.000000 | 99999.000000 | 4356.000000 | 99.000000 |
Посмотрим точность на кросс-валидации и важность признаков для случайного леса:
rf = Pipeline([('rf', RandomForestClassifier(n_jobs=-1,
class_weight='balanced',
random_state=SEED))])
# параметры кросс-валидации (стратифицированная 5-фолдовая с перемешиванием)
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=SEED)
scores = cross_val_score(estimator=rf, X=X, y=y,
cv=skf, scoring='roc_auc', n_jobs=-1)
print('scores = {} \nmean score = {:.5f} +/- {:.5f}'.format(scores, scores.mean(), scores.std()))
# важность признаков
plot_features_scores(model=rf, data=X, target=y, column_names=X.columns, model_type='rf')scores = [0.82427915 0.82290796 0.83106668 0.8192637 0.83155106]
mean score = 0.82581 +/- 0.00478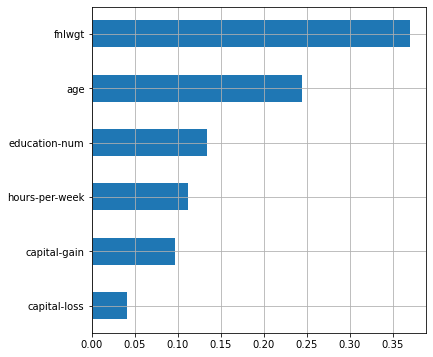
Самым важным признаком для случайного леса является fnlwgt. Это можно интерпретировать как то, что главным фактором того, что человек зарабатывает больше $50 тыс. является количество людей с такими же характеристиками. Такая интерпретация выглядит нелогичной, и происходит это потому, что модели с деревьями могут выдавать сильно смещённую оценку признаков (подробнее здесь). Притом, чем хуже настроена модель, тем сильнее может быть смещение, поэтому доверять оценкам таких моделей надо с осторожностью.
Повторим процедуру для линейной модели (с L1-регуляризацией). Для нормализации данных будем использовать метод PowerTransformer.
lr = Pipeline([('p_trans', PowerTransformer(method='yeo-johnson', standardize=True)),
('lr', LogisticRegression(solver='liblinear',
penalty='l1',
max_iter=200,
class_weight='balanced',
random_state=SEED)
)])
scores = cross_val_score(estimator=lr, X=X, y=y,
cv=skf, scoring='roc_auc', n_jobs=-1)
print('scores = {} \nmean score = {:.5f} +/- {:.5f}'.format(scores, scores.mean(), scores.std()))
plot_features_scores(model=lr, data=X, target=y, column_names=X.columns, model_type='lr')scores = [0.82034993 0.83000963 0.8348707 0.81787667 0.83548066]
mean score = 0.82772 +/- 0.00732
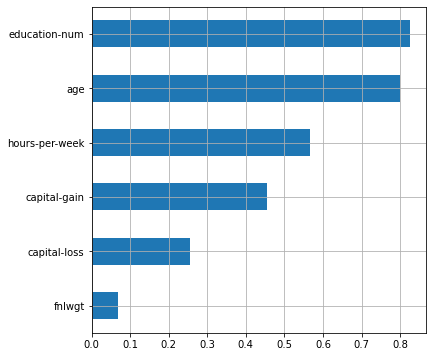
Создадим 12 шумовых признаков, элементами которых будут некоррелируемые случайные числа из выборок с нормальным, равномерным и Лапласовым распределениями. Параметры каждого распределения подбираются случайным образом независимо друг от друга.
# утановим значение генератора случайных чисел для воспроизводимости
np.random.seed(SEED)
fix, (ax1, ax2, ax3) = plt.subplots(nrows=1, ncols=3, figsize=(14,5))
ax1.set_title("normal distribution")
ax2.set_title("uniform distribution")
ax3.set_title("laplace distribution")
for i in range(4):
X.loc[:, f'norm_{i}'] = np.random.normal(loc=np.random.randint(low=0, high=10),
scale=np.random.randint(low=1, high=10),
size=(X.shape[0], 1))
X.loc[:, f'unif_{i}'] = np.random.uniform(low=np.random.randint(low=1, high=4),
high=np.random.randint(low=5, high=10),
size=(X.shape[0], 1))
X.loc[:, f'lapl_{i}'] = np.random.laplace(loc=np.random.randint(low=0, high=10),
scale=np.random.randint(low=1, high=10),
size=(X.shape[0], 1))
# визуализирукем распределения признаков
sns.kdeplot(X[f'norm_{i}'], ax=ax1)
sns.kdeplot(X[f'unif_{i}'], ax=ax2)
sns.kdeplot(X[f'lapl_{i}'], ax=ax3)
# итоговый датасет
X.head()age | fnlwgt | education-num | capital-gain | capital-loss | hours-per-week | norm_0 | unif_0 | lapl_0 | norm_1 | unif_1 | lapl_1 | norm_2 | unif_2 | lapl_2 | norm_3 | unif_3 | lapl_3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
0 | 39 | 77516 | 13 | 2174 | 0 | 40 | 0.246454 | 4.996750 | 2.311467 | 6.474587 | 6.431455 | -0.932124 | 3.773136 | 3.382773 | -1.324387 | 8.031167 | 2.142457 | 8.050902 |
1 | 50 | 83311 | 13 | 0 | 0 | 13 | -4.656718 | 4.693542 | 2.095298 | 14.622329 | 2.795007 | 6.465348 | -3.275117 | 3.787041 | 0.652694 | 7.537461 | 5.247103 | 9.014559 |
2 | 38 | 215646 | 9 | 0 | 0 | 40 | 12.788669 | 4.255611 | 22.278713 | 9.643720 | 3.533265 | 2.716441 | 4.725608 | 3.126107 | 23.410698 | 1.932907 | 4.933431 | 13.233319 |
3 | 53 | 234721 | 7 | 0 | 0 | 40 | -15.713848 | 3.989797 | 5.971506 | 8.978198 | 7.772238 | -5.402306 | 5.742672 | 3.084132 | 0.937932 | 9.435720 | 4.915537 | -3.396526 |
4 | 28 | 338409 | 13 | 0 | 0 | 40 | 20.703306 | 3.159246 | 8.718559 | 8.217148 | 4.365603 | 14.403088 | 3.023828 | 6.934299 | 4.978327 | 7.355296 | 2.551361 | 10.479218 |

Проведём кросс-валидацию на зашумлённых данных и посмотрим важность признаков:
scores = cross_val_score(estimator=rf, X=X, y=y,
cv=skf, scoring='roc_auc', n_jobs=-1)
print('scores = {} \nmean score = {:.5f} +/- {:.5f}'.format(scores, scores.mean(), scores.std()))
plot_features_scores(model=rf, data=X, target=y, column_names=X.columns, model_type='rf')scores = [0.8522425 0.85382173 0.86249657 0.84897581 0.85443027]
mean score = 0.85439 +/- 0.00447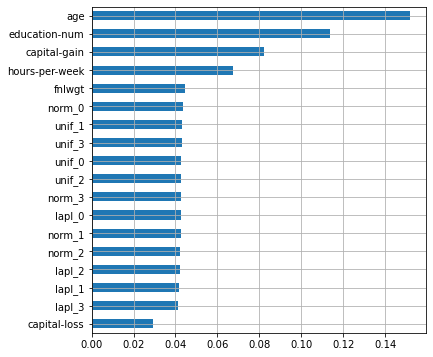
Несмотря на большое количество добавленных шумовых признаков, точность модели на кросс-валидации значительно возросла как на каждом фолде, так и в среднем! Кроме этого, все шумовые признаки имеют высокую важность, сравнимую с двумя оригинальными. Очевидно, что наша модель переобучена, однако в реальных задачах такие ситуации бывает очень сложно распознать, особенно когда при удалении некоторых признаков (про которые неизвестно – шумовые они, или нет) падает валидационная точность. Кроме того, часто бывает сложно подобрать пороговое значение важности признаков для исключения их из модели.
Посмотрим результаты для регрессии.
scores = cross_val_score(estimator=lr, X=X, y=y,
cv=skf, scoring='roc_auc', n_jobs=-1)
print('scores = {} \nmean score = {:.5f} +/- {:.5f}'.format(scores, scores.mean(), scores.std()))
plot_features_scores(model=lr, data=X, target=y, column_names=X.columns, model_type='lr')scores = [0.81993058 0.83005516 0.83446553 0.81763029 0.83543145]
mean score = 0.82750 +/- 0.00738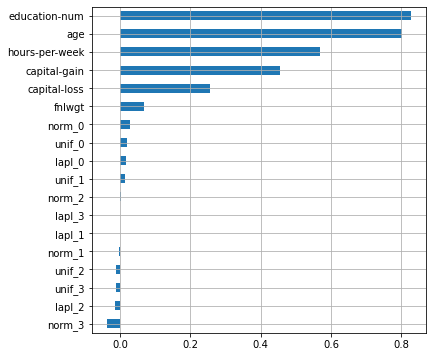
После добавления шумовых признаков модель не преобучилась, к тому же эти признки имеют значительно меньшие коэффициенты, чем оригинальные. Отметим, что распределение коэффициентов в линейных моделях часто зависит от способа нормализации или масштабирования признаков.
Проведём отбор признаков статистическими методами, для чего будем использовать обобщённый вариант SelectKBest и SelectPercentile, который называется GenericUnivariateSelect. Он принимает на вход 3 параметра – функцию оценки, режим отбора и его характеристики. В качестве функции оценки будем использовать взаимную информацию.
selector = GenericUnivariateSelect(score_func=mutual_info_classif,
mode='k_best',
param=6)
# применим к нашему датасету
selector.fit(X, y)
# метод transform вернёт массив с отобранными признаками
# выведем результаты оценки каждого признака
pd.DataFrame(data={'score':selector.scores_,
'support':selector.get_support()},
index=X.columns).sort_values(by='score',ascending=False)score | support | |
|---|---|---|
capital-gain | 0.080221 | True |
age | 0.065703 | True |
education-num | 0.064743 | True |
hours-per-week | 0.043655 | True |
capital-loss | 0.033617 | True |
fnlwgt | 0.033390 | True |
norm_3 | 0.003217 | False |
unif_3 | 0.002696 | False |
norm_0 | 0.002506 | False |
norm_2 | 0.002052 | False |
lapl_3 | 0.001201 | False |
unif_1 | 0.001144 | False |
lapl_1 | 0.000000 | False |
unif_2 | 0.000000 | False |
lapl_2 | 0.000000 | False |
lapl_0 | 0.000000 | False |
unif_0 | 0.000000 | False |
norm_1 | 0.000000 | False |
Сгенерированные нами признаки имеют низкое значение оценочной функции (scores_), поэтому в дальнейшем селектор не будет их использовать (get_support()=False).
В реальной задаче (когда количество шумовых признаков неизвестно) параметры GenericUnivariateSelect можно находить на кросс-валидации вместе с другими гиперпараметрами модели. Посмотрим, как изменится точность классификаторов после подбора их гиперпараметров, а также количества признаков селектора:
# добавим селектор в пайплайн к случайному лесу
selector = ('selector', GenericUnivariateSelect(score_func=mutual_info_classif,
mode='k_best'))
rf.steps.insert(0, selector)
# grid search
rf_params = {'selector__param': np.arange(4,10),
'rf__max_depth': np.arange(2, 16, 2),
'rf__max_features': np.arange(0.3, 0.9, 0.2)}
print('grid search results for rf')
rf_grid = grid_search(model=rf, gs_params=rf_params)grid search results for rf
scores = [0.8632776968200635, 0.8683443340928604, 0.8710308000627435, 0.8615748939138762, 0.8693334091828478],
mean score = 0.86671 +/- 0.00364
best params = {'rf__max_depth': 12, 'rf__max_features': 0.3, 'selector__param': 5}Для случайного леса средняя точность на кросс-валидации значительно выросла, а лучший результат получился всего для 5 признаков:
# выведем признаки, отобранные селектором
selected_features = [X.columns[i] for i, support
in enumerate(rf_grid.best_estimator_['selector'].get_support()) if support]
plot_features_scores(model=rf_grid.best_estimator_,
data=X, target=y, column_names=selected_features, model_type='rf')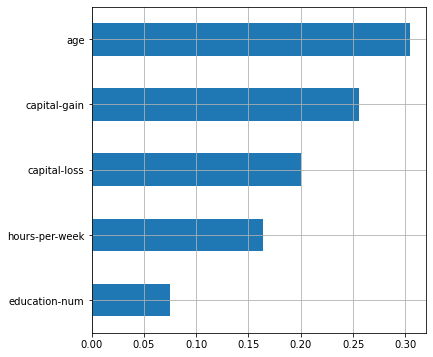
Этот результат был получен после удаления шумовых признаков и признака fnlwgt, который при первоначальной оценке был самым значимым для модели. Однако из всех оригинальных признаков он имел наименьшее значение оценочной функции в GenericUnivariateSelect. Результаты оценки важности признаков после их отбора и настройки модели имеют более логичную интерпретацию – на заработок человека влияют именно характеристики человека, а не параметры самой выборки. Таким образом, статистический отбор признаков бывает полезен для увеличения точности некоторых типов моделей и получения менее смещённой оценки при интерпретации их результатов.
Посмотрим, как изменятся коэффиценты у признаков после подбора коэффициента регуляризации у логистической регрессии.
lr_params = {'lr__C': np.logspace(-3, 1.5, 10)}
print('grid search results for lr')
lr_grid = grid_search(model=lr, gs_params=lr_params)
plot_features_scores(model=lr_grid.best_estimator_,
data=X, target=y, column_names=X.columns, model_type='lr')grid search results for lr
scores = [0.820445329307105, 0.829874053687009, 0.8346493482101578, 0.8177211039148669, 0.8354590546776963],
mean score = 0.82763 +/- 0.00729
best params = {'lr__C': 0.01}Средняя точность на кросс-валидации почти не изменилась, но скорректировались коэффициенты у шумовых признаков. Отметим, что сильная регуляризация (L1) может занулить излишнее количество признаков.
Отобранные линейной моделью признаки можно подать на вход другой модели. Для этого воспользуемся методом SelectFromModel, дадим ему на вход нашу настроенную линейную модель и обозначим граничное значение для отбора коэффициентов.
lr_selector = SelectFromModel(estimator=lr_grid.best_estimator_['lr'], prefit=True, threshold=0.1)
# посмотрим выбранные признаки признаки
pd.DataFrame(data={'score':lr_selector.estimator.coef_[0],
'support':lr_selector.get_support()},
index=X.columns).sort_values(by='score',ascending=False)score | support | |
|---|---|---|
education-num | 0.796547 | True |
age | 0.759419 | True |
hours-per-week | 0.534709 | True |
capital-gain | 0.435187 | True |
capital-loss | 0.237207 | True |
fnlwgt | 0.046698 | False |
norm_0 | 0.010349 | False |
unif_0 | 0.002101 | False |
norm_2 | 0.000000 | False |
unif_3 | 0.000000 | False |
lapl_2 | 0.000000 | False |
unif_2 | 0.000000 | False |
norm_1 | 0.000000 | False |
lapl_1 | 0.000000 | False |
unif_1 | 0.000000 | False |
lapl_0 | 0.000000 | False |
lapl_3 | 0.000000 | False |
norm_3 | -0.018818 | False |
Заключение.
В статье были рассмотрено использование фильтров и встроенных методов в задаче отбора признаков. К достоинствам фильтров можно отнести низкую стоимость вычислений (линейно зависит от количества признаков) и интерпретируемость. К недостаткам – то, что они рассматривают каждый признак изолировано, поэтому не могут выявить более сложные зависимости в данных, например, зависимость от нескольких предикторов. Эти методы хорошо подойдут, если в данных большое количество признаков, но малое количество объектов (что встречается, например, в медицинских, или биологических исследованиях).
Встроенные методы, в отличие от фильтров, требуют больших вычислительных ресурсов, а так же более точной настройки и подготовки данных. Однако, эти методы могут выявить уже более сложные зависимости. Для менее смещённой интерпретации коэффициентов признаков необходимо настроить регуляризацию модели. Важно помнить, что распределение коэфициентов у линейных моделей зависит от способа предобработки данных.
Описанные в статье методы отбора признаков можно комбинировать, либо сравнивать и подбирать их гиперпараметры используя средства sklearn или специальных библиотек.






