В этой статье я расскажу как написать свою очень простую машину опорных векторов без scikit-learn или других библиотек с готовой реализацией всего в 30 строчек на Python. Если вам хотелось разобраться в алгоритме SMO, но он показался слишком сложным, то эта статья может быть вам полезна.
Невозможно объяснить, что такоеМатрица машина опорных векторов… Ты должен увидеть это сам.
Узнав, что на Хабре есть возможность вставлять медиаэлементы, я создал небольшое демо (если вдруг не сработает — можно ещё попытать счастья с версией на гитхабе [1]). Поместите на плоскость (пространство двух фич и
и  ) несколько красных и синих точек (это наш датасет) и машина произведёт классификацию (каждая точка фона закрашивается в зависимости от того, куда был бы классифицирован соответствующий запрос). Подвигайте точки, поменяйте ядро (советую попробовать Radial Basis Functions) и твёрдость границы (константа
) несколько красных и синих точек (это наш датасет) и машина произведёт классификацию (каждая точка фона закрашивается в зависимости от того, куда был бы классифицирован соответствующий запрос). Подвигайте точки, поменяйте ядро (советую попробовать Radial Basis Functions) и твёрдость границы (константа  ). Мои извинения за ужасный код на JS — писал на нём всего несколько раз в жизни, чтобы разобраться в алгоритме используйте код на Python далее в статье.
). Мои извинения за ужасный код на JS — писал на нём всего несколько раз в жизни, чтобы разобраться в алгоритме используйте код на Python далее в статье.
Машина опорных векторов — метод машинного обучения (обучение с учителем) для решения задач классификации, регрессии, детектирования аномалий и т.д. Мы рассмотрим ее на примере задачи бинарной классификации. Наша обучающая выборка — набор векторов фич , отнесенных к одному из двух классов
, отнесенных к одному из двух классов  . Запрос на классификацию — вектор
. Запрос на классификацию — вектор  , которому мы должны приписать класс
, которому мы должны приписать класс  или
или  .
.
 В простейшем случае классы обучающей выборки можно разделить проведя всего одну прямую как на рисунке (для большего числа фич это была бы гиперплоскость). Теперь, когда придёт запрос на классификацию некоторой точки
В простейшем случае классы обучающей выборки можно разделить проведя всего одну прямую как на рисунке (для большего числа фич это была бы гиперплоскость). Теперь, когда придёт запрос на классификацию некоторой точки  , разумно отнести её к тому классу, на чьей стороне она окажется.
, разумно отнести её к тому классу, на чьей стороне она окажется.
Как выбрать лучшую прямую? Интуитивно хочется, чтобы прямая проходила посередине между классами. Для этого записывают уравнение прямой как и масштабируют параметры так, чтобы ближайшие к прямой точки датасета удовлетворяли
и масштабируют параметры так, чтобы ближайшие к прямой точки датасета удовлетворяли  (плюс или минус в зависимости от класса) — эти точки и называют опорными векторами.
(плюс или минус в зависимости от класса) — эти точки и называют опорными векторами.
 В таком случае расстояние между граничными точками классов равно
В таком случае расстояние между граничными точками классов равно  . Очевидно, мы хотим максимизировать эту величину, чтобы как можно более качественно отделить классы. Последнее эквивалентно минимизации
. Очевидно, мы хотим максимизировать эту величину, чтобы как можно более качественно отделить классы. Последнее эквивалентно минимизации  , полностью задача оптимизации записывается
, полностью задача оптимизации записывается
Если её решить, то классификация по запросу производится так
производится так
Это и есть простейшая машина опорных векторов.
А что делать в случае когда точки разных классов взаимно проникают как на рисунке?
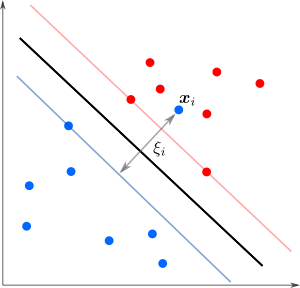 Мы уже не можем решить предыдущую задачу оптимизации — не существует параметров удовлетворяющих тем условиям. Тогда можно разрешить точкам нарушать границу на величину
Мы уже не можем решить предыдущую задачу оптимизации — не существует параметров удовлетворяющих тем условиям. Тогда можно разрешить точкам нарушать границу на величину  , но также желательно, чтобы таких нарушителей было как можно меньше. Этого можно достичь с помощью модификации целевой функции дополнительным слагаемым (регуляризация
, но также желательно, чтобы таких нарушителей было как можно меньше. Этого можно достичь с помощью модификации целевой функции дополнительным слагаемым (регуляризация  ):
):
а процедура классификации будет производиться как прежде. Здесь гиперпараметр отвечает за силу регуляризации, то есть определяет, насколько строго мы требуем от точек соблюдать границу: чем больше
отвечает за силу регуляризации, то есть определяет, насколько строго мы требуем от точек соблюдать границу: чем больше  — тем больше
— тем больше  будет обращаться в ноль и тем меньше точек будут нарушать границу. Опорными векторами в таком случае называют точки, для которых
будет обращаться в ноль и тем меньше точек будут нарушать границу. Опорными векторами в таком случае называют точки, для которых  .
.
А что если обучающая выборка напоминает логотип группы The Who и точки ни за что нельзя разделить прямой?
 Здесь нам поможет остроумная техника — трюк с ядром [4]. Однако, чтобы ее применить, нужно перейти к так называемой двойственной (или дуальной) задаче Лагранжа. Детальное ее описание можно посмотреть в Википедии [5] или в шестой лекции курса [3]. Переменные, в которых решается новая задача, называют дуальными или множителями Лагранжа. Дуальная задача часто проще изначальной и обладает хорошими дополнительными свойствами, например, она вогнута даже если изначальная задача невыпуклая. Хотя ее решение не всегда совпадает с решением изначальной задачи (разрыв двойственности), но есть ряд теорем, которые при определённых условиях гарантируют такое совпадение (сильная двойственность). И это как раз наш случай, так что можно смело перейти к двойственной задаче
Здесь нам поможет остроумная техника — трюк с ядром [4]. Однако, чтобы ее применить, нужно перейти к так называемой двойственной (или дуальной) задаче Лагранжа. Детальное ее описание можно посмотреть в Википедии [5] или в шестой лекции курса [3]. Переменные, в которых решается новая задача, называют дуальными или множителями Лагранжа. Дуальная задача часто проще изначальной и обладает хорошими дополнительными свойствами, например, она вогнута даже если изначальная задача невыпуклая. Хотя ее решение не всегда совпадает с решением изначальной задачи (разрыв двойственности), но есть ряд теорем, которые при определённых условиях гарантируют такое совпадение (сильная двойственность). И это как раз наш случай, так что можно смело перейти к двойственной задаче
где — дуальные переменные. После решения задачи максимизации требуется ещё посчитать параметр
— дуальные переменные. После решения задачи максимизации требуется ещё посчитать параметр  , который не вошёл в двойственную задачу, но нужен для классификатора
, который не вошёл в двойственную задачу, но нужен для классификатора
Классификатор можно (и нужно) переписать в терминах дуальных переменных
В чём преимущество этой записи? Обратите внимание, что все векторы из обучающей выборки входят сюда исключительно в виде скалярных произведений . Можно сначала отобразить точки на поверхность в пространстве большей размерности, и только затем вычислить скалярное произведение образов в новом пространстве. Зачем это делать видно из рисунка.
. Можно сначала отобразить точки на поверхность в пространстве большей размерности, и только затем вычислить скалярное произведение образов в новом пространстве. Зачем это делать видно из рисунка.
 При удачном отображении образы точек разделяются гиперплоскостью! На самом деле, всё ещё лучше: отображать-то и не нужно, ведь нас интересует только скалярное произведение, а не конкретные координаты точек. Так что всю процедуру можно эмулировать, заменив скалярное произведение функцией
При удачном отображении образы точек разделяются гиперплоскостью! На самом деле, всё ещё лучше: отображать-то и не нужно, ведь нас интересует только скалярное произведение, а не конкретные координаты точек. Так что всю процедуру можно эмулировать, заменив скалярное произведение функцией  , которую называют ядром. Конечно, быть ядром может не любая функция — должно хотя бы гипотетически существовать отображение
, которую называют ядром. Конечно, быть ядром может не любая функция — должно хотя бы гипотетически существовать отображение  , такое что
, такое что  . Необходимые условия определяет теорема Мерсера [6]. В реализации на Python будут представлены линейное (
. Необходимые условия определяет теорема Мерсера [6]. В реализации на Python будут представлены линейное ( ), полиномиальное (
), полиномиальное ( ) ядра и ядро радиальных базисных функций (
) ядра и ядро радиальных базисных функций ( ). Как видно из примеров, ядра могут привносить свои специфические гиперпараметры в алгоритм, что тоже будет влиять на его работу.
). Как видно из примеров, ядра могут привносить свои специфические гиперпараметры в алгоритм, что тоже будет влиять на его работу.
Возможно, вы видели видео, где действие гравитации поясняют на примере натянутой резиновой пленки в форме воронки [7]. Это работает, так как движение точки по искривленной поверхности в пространстве большой размерности эквивалентно движению её образа в пространстве меньшей размерности, если снабдить его нетривиальной метрикой. Фактически, ядро искривляет пространство.
Итак, мы у цели, осталось решить дуальную задачу, поставленную в предыдущем разделе
после чего найти параметр
а классификатор примет следующий вид
Алгоритм SMO (Sequential minimal optimization, [8]) решения дуальной задачи заключается в следующем. В цикле при помощи сложной эвристики ([9]) выбирается пара дуальных переменных и
и  , а затем по ним минимизируется целевая функция, с условием постоянства суммы
, а затем по ним минимизируется целевая функция, с условием постоянства суммы  и ограничений
и ограничений  ,
,  (настройка жёсткости границы). Условие на сумму сохраняет сумму всех
(настройка жёсткости границы). Условие на сумму сохраняет сумму всех  неизменной (ведь остальные лямбды мы не трогали). Алгоритм останавливается, когда обнаруживает достаточно хорошее соблюдение так называемых условий ККТ (Каруша-Куна-Такера [10]).
неизменной (ведь остальные лямбды мы не трогали). Алгоритм останавливается, когда обнаруживает достаточно хорошее соблюдение так называемых условий ККТ (Каруша-Куна-Такера [10]).
Я собираюсь сделать несколько упрощений.
Теперь к деталям. Информацию из обучающей выборки можно записать в виде матрицы
В дальнейшем я буду использовать обозначение с двумя индексами ( ), чтобы обратиться к элементу матрицы и с одним индексом (
), чтобы обратиться к элементу матрицы и с одним индексом ( ) для обозначения вектора-столбца матрицы. Дуальные переменные соберём в вектор-столбец
) для обозначения вектора-столбца матрицы. Дуальные переменные соберём в вектор-столбец  . Нас интересует
. Нас интересует
Допустим, на текущей итерации мы хотим максимизировать целевую функцию по индексам и
и  . Мы будем брать производные, поэтому удобно выделить слагаемые, содержащие индексы
. Мы будем брать производные, поэтому удобно выделить слагаемые, содержащие индексы  и
и  . Это просто сделать в части с суммой
. Это просто сделать в части с суммой  , а вот квадратичная форма потребует несколько преобразований.
, а вот квадратичная форма потребует несколько преобразований.
При расчёте суммирование производится по двум индексам, пускай
суммирование производится по двум индексам, пускай  и
и  . Выделим цветом пары индексов, содержащие
. Выделим цветом пары индексов, содержащие  или
или  .
.
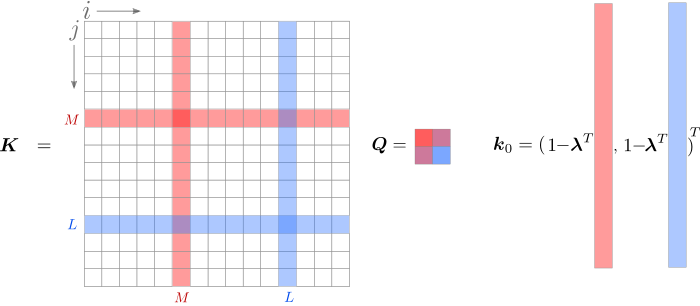
Перепишем задачу, объединив всё, что не содержит или
или  . Чтобы было легче следить за индексами, обратите внимание на
. Чтобы было легче следить за индексами, обратите внимание на  на изображении.
на изображении.
где обозначает слагаемые, не зависящие от
обозначает слагаемые, не зависящие от  или
или  . В последней строке я использовал обозначения
. В последней строке я использовал обозначения
Обратите внимание, что не зависит ни от
не зависит ни от  , ни от
, ни от 
Ядро — симметрично, поэтому и можно записать
и можно записать
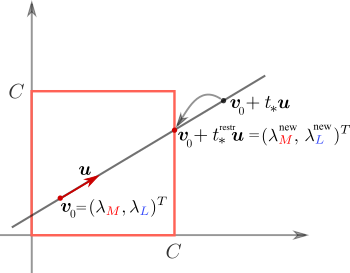
Мы хотим выполнить максимизацию так, чтобы осталось постоянным. Для этого новые значения должны лежать на прямой
осталось постоянным. Для этого новые значения должны лежать на прямой
Несложно убедиться, что для любого
В таком случае мы должны максимизировать
что легко сделать взяв производную
 Приравнивая производную к нулю, получим
Приравнивая производную к нулю, получим
На этом итерация завершается и выбираются новые индексы.
Принципиальную схему обучения упрощённой машины опорных векторов можно записать как

Давайте посмотрим на код на реальном языке программирования. Если вы не любите код в статьях, можете изучить его на гитхабе [14].
При создании объекта класса SVM можно указать гиперпараметры. Обучение производится вызовом функции fit, классы должны быть указаны как и
и  (внутри конвертируются в
(внутри конвертируются в  и
и  , сделано для большей совместимости с sklearn), размерность вектора фич допускается произвольной. Для классификации используется функция predict.
, сделано для большей совместимости с sklearn), размерность вектора фич допускается произвольной. Для классификации используется функция predict.
Стоит обратить внимание, что главный потребитель данных из матрицы — скалярные произведения с
— скалярные произведения с  (кроме них на каждой итерации используется ещё только 4 значения для формирования матрицы
(кроме них на каждой итерации используется ещё только 4 значения для формирования матрицы  ). Это означает, что эффективно мы используем только те элементы
). Это означает, что эффективно мы используем только те элементы  , что соответствуют ненулевым
, что соответствуют ненулевым  — остальные будут буквально умножены на ноль. Это важное замечание для больших размеров выборки: если количество переменных прямой задачи соответствовало размерности пространства (числу фич), то для дуальной задачи оно уже равно числу точек (размеру датасета) и квадратичная сложность по памяти может оказаться проблемой. К счастью, лишь небольшое число векторов станут опорными, а значит из всей огромной матрицы
— остальные будут буквально умножены на ноль. Это важное замечание для больших размеров выборки: если количество переменных прямой задачи соответствовало размерности пространства (числу фич), то для дуальной задачи оно уже равно числу точек (размеру датасета) и квадратичная сложность по памяти может оказаться проблемой. К счастью, лишь небольшое число векторов станут опорными, а значит из всей огромной матрицы  нам понадобятся для расчётов всего несколько элементов, которые можно или пересчитывать каждый раз, или же использовать ленивые вычисления.
нам понадобятся для расчётов всего несколько элементов, которые можно или пересчитывать каждый раз, или же использовать ленивые вычисления.
Не то, чтобы данное сравнение имело особый смысл, ведь речь идёт о крайне упрощённом алгоритме, разработанном исключительно в целях обучения студентов, но всё же. Для тестирования (и чтобы посмотреть как этим всем пользоваться) можно выполнить следующее (этот код тоже есть на гитхаб [14]).
После запуска будут сгенерированы картинки, но так как алгоритм рандомизированный, то они будут слегка отличаться для каждого запуска. Вот пример работы упрощённого алгоритма (слева направо: линейное, полиномиальное и rbf ядра)
А это результат работы промышленной версии машины опорных векторов.
Если размерность кажется слишком маленькой, то можно ещё протестировать на MNIST
кажется слишком маленькой, то можно ещё протестировать на MNIST
Для MNIST я попробовал несколько случайных пар классов (упрощённый алгоритм поддерживает только бинарную классификацию), но разницы в работе упрощённого алгоритма и sklearn не обнаружил. Представление о качестве даёт следующая confusion matrix.

Спасибо всем, кто дочитал до конца. В этой статье мы рассмотрели упрощённую учебную реализацию машины опорных векторов. Конечно, она не может состязаться с промышленным образцом, но благодаря крайней простоте и компактному коду на Python, а также тому, что все основные идеи SMO были сохранены, эта версия SVM вполне может занять своё место в учебной аудитории. Стоит отметить, что алгоритм проще не только весьма мудрёного алгоритма [9], но даже его упрощённой версии от Стэнфордского университета [11]. Все-таки машина опорных векторов в 30 строчках — это красиво.
Невозможно объяснить, что такое
Узнав, что на Хабре есть возможность вставлять медиаэлементы, я создал небольшое демо (если вдруг не сработает — можно ещё попытать счастья с версией на гитхабе [1]). Поместите на плоскость (пространство двух фич
Содержание
- В следующем разделе я бегло опишу математическую постановку задачи обучения машины опорных векторов, к какой задаче оптимизации она сводится, а также некоторые гиперпараметры, позволяющие регулировать работу алгоритма. Этот материал лишь подводящий к нашей конечной цели и нужен чтобы вспомнить ключевые факты, если такое напоминание не требуется — можете его пропустить без ущерба для понимания дальнейших частей. Если же вы ранее не сталкивались с машинами опорных векторов, то понадобиться куда более полное изложение — обратите внимание на соответствующую лекцию уже ставшего классикой курса Воронцова [2] или на десятую лекцию курса [3], в которую, кстати, входит представленный ниже метод.
- В разделе «Алгоритм SMO» я подробно расскажу как решить поставленную задачу минимизации упрощенным методом SMO и в чём, собственно, состоит упрощение. Будут выкладки, но их объём гораздо меньше, чем в тех подходах к SMO, что доводилось видеть мне.
- Наконец, в разделе «Реализация» будет представлен код классификатора на Python и схема обучения в псевдокоде.
- Узнать насколько алгоритм удался можно в разделе «Сравнение с sklearn.svc.svm» — там приведено визуальное сравнение для небольших датасетов в 2D и confusion matrix для двух классов из MNIST.
- А в «Заключении» что-нибудь да заключим.
Машина опорных векторов
Машина опорных векторов — метод машинного обучения (обучение с учителем) для решения задач классификации, регрессии, детектирования аномалий и т.д. Мы рассмотрим ее на примере задачи бинарной классификации. Наша обучающая выборка — набор векторов фич
 В простейшем случае классы обучающей выборки можно разделить проведя всего одну прямую как на рисунке (для большего числа фич это была бы гиперплоскость). Теперь, когда придёт запрос на классификацию некоторой точки
В простейшем случае классы обучающей выборки можно разделить проведя всего одну прямую как на рисунке (для большего числа фич это была бы гиперплоскость). Теперь, когда придёт запрос на классификацию некоторой точки Как выбрать лучшую прямую? Интуитивно хочется, чтобы прямая проходила посередине между классами. Для этого записывают уравнение прямой как
 В таком случае расстояние между граничными точками классов равно
В таком случае расстояние между граничными точками классов равно Если её решить, то классификация по запросу
Это и есть простейшая машина опорных векторов.
А что делать в случае когда точки разных классов взаимно проникают как на рисунке?
 Мы уже не можем решить предыдущую задачу оптимизации — не существует параметров удовлетворяющих тем условиям. Тогда можно разрешить точкам нарушать границу на величину
Мы уже не можем решить предыдущую задачу оптимизации — не существует параметров удовлетворяющих тем условиям. Тогда можно разрешить точкам нарушать границу на величину а процедура классификации будет производиться как прежде. Здесь гиперпараметр
А что если обучающая выборка напоминает логотип группы The Who и точки ни за что нельзя разделить прямой?
 Здесь нам поможет остроумная техника — трюк с ядром [4]. Однако, чтобы ее применить, нужно перейти к так называемой двойственной (или дуальной) задаче Лагранжа. Детальное ее описание можно посмотреть в Википедии [5] или в шестой лекции курса [3]. Переменные, в которых решается новая задача, называют дуальными или множителями Лагранжа. Дуальная задача часто проще изначальной и обладает хорошими дополнительными свойствами, например, она вогнута даже если изначальная задача невыпуклая. Хотя ее решение не всегда совпадает с решением изначальной задачи (разрыв двойственности), но есть ряд теорем, которые при определённых условиях гарантируют такое совпадение (сильная двойственность). И это как раз наш случай, так что можно смело перейти к двойственной задаче
Здесь нам поможет остроумная техника — трюк с ядром [4]. Однако, чтобы ее применить, нужно перейти к так называемой двойственной (или дуальной) задаче Лагранжа. Детальное ее описание можно посмотреть в Википедии [5] или в шестой лекции курса [3]. Переменные, в которых решается новая задача, называют дуальными или множителями Лагранжа. Дуальная задача часто проще изначальной и обладает хорошими дополнительными свойствами, например, она вогнута даже если изначальная задача невыпуклая. Хотя ее решение не всегда совпадает с решением изначальной задачи (разрыв двойственности), но есть ряд теорем, которые при определённых условиях гарантируют такое совпадение (сильная двойственность). И это как раз наш случай, так что можно смело перейти к двойственной задачегде
Классификатор можно (и нужно) переписать в терминах дуальных переменных
В чём преимущество этой записи? Обратите внимание, что все векторы из обучающей выборки входят сюда исключительно в виде скалярных произведений
 При удачном отображении образы точек разделяются гиперплоскостью! На самом деле, всё ещё лучше: отображать-то и не нужно, ведь нас интересует только скалярное произведение, а не конкретные координаты точек. Так что всю процедуру можно эмулировать, заменив скалярное произведение функцией
При удачном отображении образы точек разделяются гиперплоскостью! На самом деле, всё ещё лучше: отображать-то и не нужно, ведь нас интересует только скалярное произведение, а не конкретные координаты точек. Так что всю процедуру можно эмулировать, заменив скалярное произведение функцией Возможно, вы видели видео, где действие гравитации поясняют на примере натянутой резиновой пленки в форме воронки [7]. Это работает, так как движение точки по искривленной поверхности в пространстве большой размерности эквивалентно движению её образа в пространстве меньшей размерности, если снабдить его нетривиальной метрикой. Фактически, ядро искривляет пространство.
Алгоритм SMO
Итак, мы у цели, осталось решить дуальную задачу, поставленную в предыдущем разделе
после чего найти параметр
а классификатор примет следующий вид
Алгоритм SMO (Sequential minimal optimization, [8]) решения дуальной задачи заключается в следующем. В цикле при помощи сложной эвристики ([9]) выбирается пара дуальных переменных
Я собираюсь сделать несколько упрощений.
- Откажусь от сложной эвристики выбора индексов (так сделано в курсе Стэнфордского университета [11]) и буду итерировать по одному индексу, а второй — выбирать случайным образом.
- Откажусь от проверки ККТ и буду выполнять наперёд заданное число итераций.
- В самой процедуре оптимизации, в отличии от классической работы [9] или стэнфордского подхода [11], воспользуюсь векторным уравнением прямой. Это существенно упростит выкладки (сравните объём [12] и [13]).
Теперь к деталям. Информацию из обучающей выборки можно записать в виде матрицы
В дальнейшем я буду использовать обозначение с двумя индексами (
Допустим, на текущей итерации мы хотим максимизировать целевую функцию по индексам
При расчёте

Перепишем задачу, объединив всё, что не содержит
где
Обратите внимание, что
Ядро — симметрично, поэтому
Мы хотим выполнить максимизацию так, чтобы
Несложно убедиться, что для любого
В таком случае мы должны максимизировать
что легко сделать взяв производную
 Приравнивая производную к нулю, получим
Приравнивая производную к нулю, получимНа этом итерация завершается и выбираются новые индексы.
Реализация
Принципиальную схему обучения упрощённой машины опорных векторов можно записать как

Давайте посмотрим на код на реальном языке программирования. Если вы не любите код в статьях, можете изучить его на гитхабе [14].
Исходный код упрощённой машины опорных векторов
import numpy as np
class SVM:
def __init__(self, kernel='linear', C=10000.0, max_iter=100000, degree=3, gamma=1):
self.kernel = {'poly' : lambda x,y: np.dot(x, y.T)**degree,
'rbf': lambda x,y: np.exp(-gamma*np.sum((y-x[:,np.newaxis])**2,axis=-1)),
'linear': lambda x,y: np.dot(x, y.T)}[kernel]
self.C = C
self.max_iter = max_iter
# ограничение параметра t, чтобы новые лямбды не покидали границ квадрата
def restrict_to_square(self, t, v0, u):
t = (np.clip(v0 + t*u, 0, self.C) - v0)[1]/u[1]
return (np.clip(v0 + t*u, 0, self.C) - v0)[0]/u[0]
def fit(self, X, y):
self.X = X.copy()
# преобразование классов 0,1 в -1,+1; для лучшей совместимости с sklearn
self.y = y * 2 - 1
self.lambdas = np.zeros_like(self.y, dtype=float)
# формула (3)
self.K = self.kernel(self.X, self.X) * self.y[:,np.newaxis] * self.y
# выполняем self.max_iter итераций
for _ in range(self.max_iter):
# проходим по всем лямбда
for idxM in range(len(self.lambdas)):
# idxL выбираем случайно
idxL = np.random.randint(0, len(self.lambdas))
# формула (4с)
Q = self.K[[[idxM, idxM], [idxL, idxL]], [[idxM, idxL], [idxM, idxL]]]
# формула (4a)
v0 = self.lambdas[[idxM, idxL]]
# формула (4b)
k0 = 1 - np.sum(self.lambdas * self.K[[idxM, idxL]], axis=1)
# формула (4d)
u = np.array([-self.y[idxL], self.y[idxM]])
# регуляризированная формула (5), регуляризация только для idxM = idxL
t_max = np.dot(k0, u) / (np.dot(np.dot(Q, u), u) + 1E-15)
self.lambdas[[idxM, idxL]] = v0 + u * self.restrict_to_square(t_max, v0, u)
# найти индексы опорных векторов
idx, = np.nonzero(self.lambdas > 1E-15)
# формула (1)
self.b = np.mean((1.0-np.sum(self.K[idx]*self.lambdas, axis=1))*self.y[idx])
def decision_function(self, X):
return np.sum(self.kernel(X, self.X) * self.y * self.lambdas, axis=1) + self.b
def predict(self, X):
# преобразование классов -1,+1 в 0,1; для лучшей совместимости с sklearn
return (np.sign(self.decision_function(X)) + 1) // 2
При создании объекта класса SVM можно указать гиперпараметры. Обучение производится вызовом функции fit, классы должны быть указаны как
Стоит обратить внимание, что главный потребитель данных из матрицы
Сравнение с sklearn.svm.SVC
Не то, чтобы данное сравнение имело особый смысл, ведь речь идёт о крайне упрощённом алгоритме, разработанном исключительно в целях обучения студентов, но всё же. Для тестирования (и чтобы посмотреть как этим всем пользоваться) можно выполнить следующее (этот код тоже есть на гитхаб [14]).
Сравнение с sklearn.svm.SVC на простом двумерном датасете
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
from sklearn.datasets import make_blobs, make_circles
from matplotlib.colors import ListedColormap
def test_plot(X, y, svm_model, axes, title):
plt.axes(axes)
xlim = [np.min(X[:, 0]), np.max(X[:, 0])]
ylim = [np.min(X[:, 1]), np.max(X[:, 1])]
xx, yy = np.meshgrid(np.linspace(*xlim, num=700), np.linspace(*ylim, num=700))
rgb=np.array([[210, 0, 0], [0, 0, 150]])/255.0
svm_model.fit(X, y)
z_model = svm_model.decision_function(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plt.contour(xx, yy, z_model, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
plt.contourf(xx, yy, np.sign(z_model.reshape(xx.shape)), alpha=0.3, levels=2, cmap=ListedColormap(rgb), zorder=1)
plt.title(title)
X, y = make_circles(100, factor=.1, noise=.1)
fig, axs = plt.subplots(nrows=1,ncols=2,figsize=(12,4))
test_plot(X, y, SVM(kernel='rbf', C=10, max_iter=60, gamma=1), axs[0], 'OUR ALGORITHM')
test_plot(X, y, SVC(kernel='rbf', C=10, gamma=1), axs[1], 'sklearn.svm.SVC')
X, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=1.4)
fig, axs = plt.subplots(nrows=1,ncols=2,figsize=(12,4))
test_plot(X, y, SVM(kernel='linear', C=10, max_iter=60), axs[0], 'OUR ALGORITHM')
test_plot(X, y, SVC(kernel='linear', C=10), axs[1], 'sklearn.svm.SVC')
fig, axs = plt.subplots(nrows=1,ncols=2,figsize=(12,4))
test_plot(X, y, SVM(kernel='poly', C=5, max_iter=60, degree=3), axs[0], 'OUR ALGORITHM')
test_plot(X, y, SVC(kernel='poly', C=5, degree=3), axs[1], 'sklearn.svm.SVC')
После запуска будут сгенерированы картинки, но так как алгоритм рандомизированный, то они будут слегка отличаться для каждого запуска. Вот пример работы упрощённого алгоритма (слева направо: линейное, полиномиальное и rbf ядра)
 |
 |
 |
А это результат работы промышленной версии машины опорных векторов.
 |
 |
 |
Если размерность
Сравнение с sklearn.svm.SVC на 2-х классах из MNIST
from sklearn import datasets, svm
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns
class_A = 3
class_B = 8
digits = datasets.load_digits()
mask = (digits.target == class_A) | (digits.target == class_B)
data = digits.images.reshape((len(digits.images), -1))[mask]
target = digits.target[mask] // max([class_A, class_B]) # rescale to 0,1
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.5, shuffle=True)
def plot_confusion(clf):
clf.fit(X_train, y_train)
y_fit = clf.predict(X_test)
mat = confusion_matrix(y_test, y_fit)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False, xticklabels=[class_A,class_B], yticklabels=[class_A,class_B])
plt.xlabel('true label')
plt.ylabel('predicted label');
plt.show()
print('sklearn:')
plot_confusion(svm.SVC(C=1.0, kernel='rbf', gamma=0.001))
print('custom svm:')
plot_confusion(SVM(kernel='rbf', C=1.0, max_iter=60, gamma=0.001))
Для MNIST я попробовал несколько случайных пар классов (упрощённый алгоритм поддерживает только бинарную классификацию), но разницы в работе упрощённого алгоритма и sklearn не обнаружил. Представление о качестве даёт следующая confusion matrix.

Заключение
Спасибо всем, кто дочитал до конца. В этой статье мы рассмотрели упрощённую учебную реализацию машины опорных векторов. Конечно, она не может состязаться с промышленным образцом, но благодаря крайней простоте и компактному коду на Python, а также тому, что все основные идеи SMO были сохранены, эта версия SVM вполне может занять своё место в учебной аудитории. Стоит отметить, что алгоритм проще не только весьма мудрёного алгоритма [9], но даже его упрощённой версии от Стэнфордского университета [11]. Все-таки машина опорных векторов в 30 строчках — это красиво.
Список литературы
- https://fbeilstein.github.io/simplest_smo_ever/
- страница на http://www.machinelearning.ru
- «Начала Машинного Обучения», КАУ
- https://en.wikipedia.org/wiki/Kernel_method
- https://en.wikipedia.org/wiki/Duality_(optimization)
- Статья на http://www.machinelearning.ru
- https://www.youtube.com/watch?v=MTY1Kje0yLg
- https://en.wikipedia.org/wiki/Sequential_minimal_optimization
- https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/tr-98-14.pdf
- https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions
- http://cs229.stanford.edu/materials/smo.pdf
- https://www.researchgate.net/publication/344460740_Yet_more_simple_SMO_algorithm
- http://fourier.eng.hmc.edu/e176/lectures/ch9/node9.html
- https://github.com/fbeilstein/simplest_smo_ever






