Комментарии 153
Мало что понял, но очень интересно. Не хватает кармы поставить плюс.
Получается, что если детектор будет работать в комплексном пространстве, то будет сохраняться та же картина интерференции. Но детектор у нас обычный, работающий только в вещественном пространстве, поэтому одно пространственное измерение (хм, или не одно?) — теряется, и на детекторе мы видим частицу только в том месте, где амплитуды совпали с детектором.
Кратко освежим в памяти, модуль комплексного числа
…
видно, что (sqrt(-1))^2 = 1
Но ведь -1 же, разве нет?
И далее сумма квадратов раскладывается как произведение, но это преобразование можно применять к разнице квадратов, не к сумме.
Тоже резануло глаз, ведь модуль определяется как корень из x^2+y^2 = x^2-(iy)^2 = (x+iy)(x-iy).
Рассуждение про многочлены для обоснования взятия квадрата модуля не очень убедило, ведь волновая функция не обязательно будет полиномом. Вероятно, это то место, когда сравнение с экспериментом определяет.
Рассуждение про многочлены для обоснования взятия квадрата модуля не очень убедило
Точно! Кажется абсолютно искусственным. Можно приближать функции многочленами, а можно и не многочленами. В итоге всё сводится к тому, что можно любое неотрицательное вещественное значение представить как произведение сопряжённых комплексных. Правда такое разложение неоднозначно, что смущает ещё больше. И если уж выбирать произвольные подходящие математические объекты, то почему бы не представлять эти значения, как модуль кватерниона, например?
ведь волновая функция не обязательно будет полиномом.
Я больше скажу: если приближать её так, как предложено в статье, то полученный для n точек многочлен будет совпадать с функцией только в этих n точках, но при росте n будет всё сильнее расходиться с ней во всех остальных точках. Хотя пример кода при этом использует, судя по документации к polyfit, метод наименьших квадратов, и приближает в этом смысле лучше, но возвращает многочлен, который не обязан проходить ровно через заданные точки.
Порядок мы вводим сами какой захотим. Какой порядок не сохраняется?
Видимо речь, о том же порядке, который имеем ввиду, что вещественные числа — это "непрерывное упорядоченное поле"
а «превратить поле комплексных чисел в упорядоченное поле невозможно, потому что в упорядоченном поле квадрат любого элемента неотрицателен, и мнимая единица в нём не может существовать»
В соответствие с этим графиком можно получить форму, так называемых, электронных орбиталей — областей вокруг ядра атома, в которых взаимодействие с электроном наиболее вероятно, показанных справа:
наверное опечатка, имеется ввиду "… нахождение электрона наиболее вероятно..."
Так частица же сама с собой взаимодействует
а вроде же был эксперимент с одной частицей, которая тоже дала интерференционную картину, чем ещё больше всех запутала? или я что-то путаю?
технические решения, разработанные благодаря применению аппарата квантовой механики, прочно вошли в повседневную жизнь современного общества
Например?
И согласно принципу неопределенности, чем точнее мы будем фиксировать координату объекта в пространстве-времени $Δx$, тем меньше информации мы сможем получить о его импульсе.
Если мы можем получить точную координату частицы в любой момент времени, то знаем и импульс и траекторию.
когда размер щели станет сопоставим с длиной волны фотона, то траектории фотонов на выходе из щели станут все менее предсказуемыми и световое пятно начнет расплываться в ширину.
Это особенность щелей, а не света. Возьмите линзу и получите аккуратную точку на фокусном расстоянии. Кстати, обратите внимание на 34 секунду, где видна интерференционная картина от одной-то щели. Вызвана она по всей видимости отражениями от краёв щели.
И если мы начнем сжимать волну по высоте, то она будет расползаться в длину и наоборот.
Частота звука зависит от его громкости? Довольно смелое заявление.
А что, если мы добавим волнам вероятности такое свойство, благодаря которому они смогут интерферировать?
Звучит как притягивание слона за уши. Колебательные процессы, конечно, удобно описывать комплексными числами, но сами по себе они никакого физического воплощения не имеют. Это чистая математическая абстракция, никакого отношения к реальности не имеющая.
Такое распределение вероятности выглядит очень странно, ведь попасть из одной сферы в другую, не пересекая вложенную между ними — невозможно.
То, что вероятность его там "засечь" (кстати, как?) крайне мала (нулевая он лишь в одной точке, судя по модели) не означает, что он эту зону не пересекает.
если думать об электроне, как об амплитуде вероятности, то все объясняется вполне естественно
Если думать об электроне, как об амплитуде вероятности положения… электрона, то можно уйти в бесконечную рекурсию и помереть от голода.
Продолжаем задавать неудобные вопросы..
вторичный фронт, который с уменьшением размера щели все больше будет походить на волну от точечного источника.
А такая волна в вакууме должна равномерно залить экран. Наблюдается ли такой эффект?
измерить скорость — отправляем на встречу электромагнитную волну
Есть много способов измерения скорости. В том числе и пассивные. В том числе ретроспективные. Например, по месту и углу падения можно рассчитать траекторию и скорость.
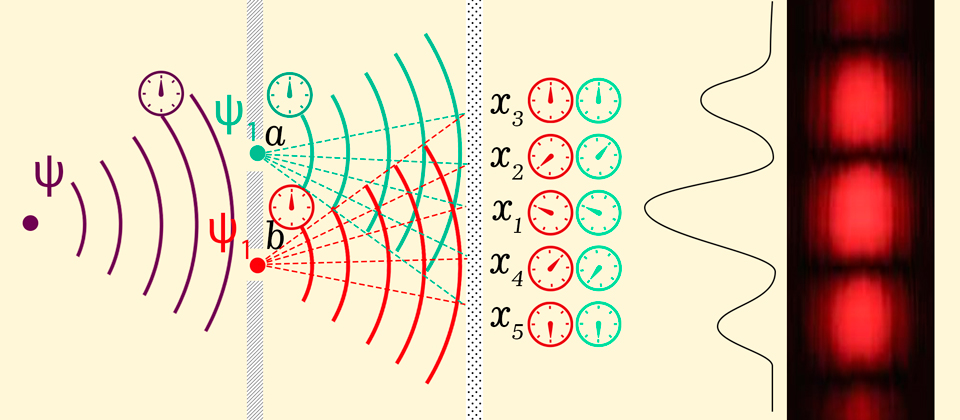
точки образуют интерференционную картину, которая соответствует прохождению волны через две щели
Рассчётная картинка предполагает наличие зон с интенсивностью близкой к нулю. А на фотографиях (или это опять кривой рендер за фото выдаётся?) мы видим равномерное залитие с периодическими всплесками. А на этом фото мы вообще видим пару внезапных всплесков интенсивности слева и справа:

Периодичность-то есть, но на интерференцию не очень-то похоже.
даже если детектор микроскопический, он все равно будет состоять из огромного количества атомов, например даже в одной сотой грамма железа содержится порядка $10^{20}$ атомов
Так и края щели состоят из не меньшего числа атомов. Почему они никак не влияют на интерференцию, а детектор вдруг влияет? Тем более, что он может быть встроен в этот самый край.
Продолжаем задавать неудобные вопросы..
Почему же они неудобные? Наоборот, почти очевидные для любого кто хоть как-то изучил основы. Постараюсь кратко ответить ниже.
технические решения, разработанные благодаря применению аппарата квантовой механики, прочно вошли в повседневную жизнь современного общества
Например?
Лазеры, полупроводники.
Если мы можем получить точную координату частицы в любой момент времени, то знаем и импульс и траекторию.
Нет. Например, измерили координату в момент t=0 — получили x=0, измерили в t=1 — получили x=1. Импульс по этим данным не узнать.
Это особенность щелей, а не света. Возьмите линзу и получите аккуратную точку на фокусном расстоянии.
Серьёзно? Где же найти такую волшебную линзу, которая даёт идеальную точку в фокусе? Про реальные линзы см. https://ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%81%D0%BA_%D0%AD%D0%B9%D1%80%D0%B8.
А такая волна [от точечного источника] в вакууме должна равномерно залить экран.
С чего бы точечному источнику равномерно заливать экран? Наоборот, такого никогда не бывает.
Рассчётная картинка предполагает наличие зон с интенсивностью близкой к нулю. А на фотографиях мы видим равномерное залитие с периодическими всплесками.
Вполне себе интенсивность спадающая к нулю (чёрный цвет) между пиками на картинке из поста:
Можете легко ещё множество фотографий нагуглить.
Почему же они неудобные?
Потому что 6 минусов.
Лазеры, полупроводники.
И где там используется квантмех? Точнее, что в них нельзя без квантмеха описать?
Например, измерили координату в момент t=0 — получили x=0, измерили в t=1 — получили x=1. Импульс по этим данным не узнать.
m*dx/dt — всё замечательно узнаётся.
Где же найти такую волшебную линзу, которая даёт идеальную точку в фокусе?
Не идеальную, а аккуратную. А не тот расколбас, что в статье.
С чего бы точечному источнику равномерно заливать экран? Наоборот, такого никогда не бывает.
Потому что одинаковая амплитуда доходит до каждой точки экрана. Или вы хотите сказать, что свет устаёт?!?
Вполне себе интенсивность спадающая к нулю (чёрный цвет) между пиками на картинке из поста
Тут речь про вот эти картинки: https://iopscience.iop.org/article/10.1088/1367-2630/15/3/033018/pdf
- Почему же они неудобные?
Потому что 6 минусов.
Интересная у вас логика. Вообще-то в комментарии, к которому минусы, вы вопросов почти не задали. Вместо этого попытались самоуверенно — и неправильно — указать автору на ошибки/неточности.
- Лазеры, полупроводники.
И где там используется квантмех?
Да по сути везде, почитайте литературу про это если интересует подробнее.
m*dx/dt — всё замечательно узнаётся.
Что здесь имеется в виду под dx и dt? Если разница по времени и координате между соседними измерениями, то такое вычисление даст всего лишь "средний" в некотором смысле импульс за прошедшее время. А речь о том, что нельзя одновременно измерить точно координату и импульс.
- Где же найти такую волшебную линзу, которая даёт идеальную точку в фокусе?
Не идеальную, а аккуратную. А не тот расколбас, что в статье.
Ничего не понял. Никакая реальная линза вам точку в фокусе не даст, в самом лучшем случае там будут некие расходящиеся круги.
- С чего бы точечному источнику равномерно заливать экран? Наоборот, такого никогда не бывает.
Потому что одинаковая амплитуда доходит до каждой точки экрана. Или вы хотите сказать, что свет устаёт?!?
Даже если кроме точечного источника и экрана ничего нет, то равномерности взяться решительно неоткуда. Области экрана ближе к источнику будут ярче.
Тут речь про вот эти картинки: https://...
Где "тут"? По-умолчанию в коментах под определённым постом логично обсуждать картинки, приведённые в нём.
такое вычисление даст всего лишь "средний" в некотором смысле импульс за прошедшее время.
Если частица движется равномерно, то мгновенные скорости на промежутке совпадают со средней. Если не равномерно — по трём точкам можно найти ускорение.
Ничего не понял.
На картинки посмотрите:

Области экрана ближе к источнику будут ярче.
Это так только для корпускул и для затухающих в среде волн. В вакууме свет не устаёт, так что засветка должна быть равномерной.
Где "тут"? По-умолчанию в коментах под определённым постом логично обсуждать картинки, приведённые в нём.
А вы по ссылкам на источники из поста не ходите?
Если не равномерно — по трём точкам можно найти ускорение.
Это если ускорение постоянное
Если частица движется равномерно, то мгновенные скорости на промежутке совпадают со средней.
Для начала надо чтобы мгновенная скорость вообще существовала. Для квантовых частиц при последовательном измерении двух положений отношение разности положений к интервалу времени не стремится к определённому пределу при уменьшении промежутка между измерениями (экспериментальный факт).
Из существования погрешности измерений никак не следует принципиальная недереминированность измеряемой величины.
Погрешность или нет, а факт, что классическое определения понятия мгновенной скорости к квантовой частице неприменимо. Поэтому прежде чем утверждать, что "если частица движется равномерно, то мгновенные скорости на промежутке совпадают со средней", надо сначала дать определение "мгновенной скорости" и "равномерного движения".
Не следует. Но есть 2 пути
1) Говорить, что мы просто плохо проводим эксперименты, и сейчас что-то придумаем получше. Пока не придумали.
2) Постулировать, что так оно и есть, и строить теорию на этой основе. Факт недетерминированности просто истекает из того, что модель "электрон — это частица" явно недостаточна. Такой моделью не описать, например, дифракцию потока электронов на кристаллической решётке. Поэтому и нужна ещё другая модель в таких случаях. Из-за того, что обе модели справедливы и можно вывести принцип неопределённости.
В итоге, 1-й вариант ведёт в тупик, а вот 2-й вариант просто работает лучше, и позволяет разом описать все те трудности, с которыми столкнуласть классическая физика
Формально, есть уже куча чисто классических моделей описывающих различные квантовые эффекты, (например дифракцию потока электронов на кристаллической решётке (не разбирал — увидел в ссылках)). Просто у них у всех разная степень костыльности, они не универсальны, в них лень разбираться, порой они плохо проработаны из-за нехватки вложенных человекочасов. А бывает, что они математически согласованы и близки повседневному восприятию, но не дают никаких явных преимуществ
Если мы сейчас не можем что-то объяснить, то повод ли это постулировать это что-то принципиально необъяснимым и более не искать иных объяснений?
Касательно дифракции, я нигде не видел рассмотрения влияния периодически колеблющихся электронов в краях щели на движение пролетающих мимо электронов.
Если мы сейчас не можем что-то объяснить, то повод ли это постулировать это что-то принципиально необъяснимым и более не искать иных объяснений?
Если не можем объяснить — надо искать. Только ведь мы как раз можем объяснить. Квантовая механика как раз и объясняет. А вот то, что вам объяснение не нравится, — вот это как раз совсем не повод искать другое.
"Объяснение" квантовой механики порождает больше вопросов, чем ответов. С тем же успехом и температуру можно объяснять волновой функцией положения атомов.
Вы сейчас выдаёте желаемое за действительное. Не надо так.
Для многих людей очевидно, что перо падает медленнее камня, солнечное пятно от треугольной дырки тоже треугольное, а металлические предметы в комнате более холодные, чем подушка. Увы, не всегда ваш опыт подсказывает верные вещи.
Квантовая механика одной формулой и парой постулатов объяснила как минимум 4 вещи (спектр, фотоэффект, строение атома и двущелевой опыт), которые лучшие умы планеты не смогли объяснить десятками лет, топтаясь в консервативных идеях. А потом объяснила и предсказала ешё целую кучу других эффектов. Где же тут больше вопросов? То, что она не попадает под ваше определение очевидного и не согласуется с вашим опытом не проблема теории.
спектр, фотоэффект, строение атома и двущелевой опыт
А что там в них не может быть объяснено без привлечения принципиальной неопределённости?
Квантовая механика одной формулой
Там не одна формула.
Где же тут больше вопросов?
Да вот эта вся ерунда про субъективность наблюдения.
Ну или вот хотя бы про однощелевую дифракцию мне так никто и не ответил.
Лазеры, полупроводники.
И где там используется квантмех? Точнее, что в них нельзя без квантмеха описать?
Полупроводники — туннельный диод. В классической физике туннельный эффект отсутствует.
Лазеры — вынужденное излучение. У классической физики возникают проблемы когда надо объяснить, почему это вынужденное излучение будет, например, монохроматическим.
В классической физике туннельный эффект отсутствует.
Это если рассматривать идеальную круглую частице в вакууме, а не группу частиц, где средняя по больнице частица пересечь барьер не может, а отдельная шустрая частица — может.
У классической физики возникают проблемы когда надо объяснить, почему это вынужденное излучение будет, например, монохроматическим.
А с чего бы ему быть полихроматическим, если оно возникает в однородных условиях?
А с чего бы ему быть полихроматическим, если оно возникает в однородных условиях?
Как однородные условия влияют на частоту? Согласно классической физике, атом, поглативший энергию, излучать её может на любой длине волны. Вот облучаем мы светом кристалл. Часть энергии уходит на нагрев, то есть превращается в тепловое излучение. Почему на выходе частота строго определённая? Вот поступило в атом 10 единиц энергии. В тепло может уйти как 5, так и pi/2, а остальное излучится.
Но в жизни (и на бумаге, если пользоваться квантмехом), в тепло всегда уходит только 6, а излучается 4. Да ещё и когерентно.
Ну и в качестве факультатива — постройте с помощью классической физики непротиворечивую модель атома, да так, чтобы она согласовывалась со всеми экспериментами.
Как однородные условия влияют на частоту?
Одинаковые условия — одинаковый результат.
Согласно классической физике, атом, поглативший энергию, излучать её может на любой длине волны.
Это какой закон об этом говорит?
В тепло может уйти как 5, так и pi/2, а остальное излучится.
Классическая физика ни коим образом не исключает скачкообразные процессы. Яркий пример — сила трения покоя, которую надо преодолеть, чтобы началось движение.
Ну и в качестве факультатива
Убавьте свой менторский тон, он вас не красит.
Это какой закон об этом говорит?
Вообще никакой, тут я не прав. Но просто потому что классическая физика не объясняет строение атома. Термодинамика объясняет законы излучения для системы из атомов. И в ней вещество может поглотить сколь угодно малое количество энергии. Однако, оперируя только этими законами рассчитать спектральную плотность уже не вышло.
Я вот не знаю, например, как можно объяснить с классической точки зрения такое явление как лазер. Светим светом на кристалл/газ, и он, помимо теплового излучения начинает излучать почему-то ещё и монохроматическое когерентное. Какие процессы к этому приводят? Как рассчитать длину волны?
Яркий пример — сила трения покоя, которую надо преодолеть, чтобы началось движение.
Это пример преодоление потенциальной ямы. Кванты немного про другое
Это пример преодоление потенциальной ямы. Кванты немного про другое
Чтобы запустить квант света тоже нужно преодолеть потенциальную яму.
Так в вашем представлении кванты света всё-таки есть или нет?
Если вы говорите "квант", то автоматом тянется квантмех, в основе которого лежит соотношение неопределённостей, которое корнями идёт в уравнение Шрёдингера.
Если же не признавать квантмех, то тогда свет — это только волна, без каких-либо квантов и излучиться может любое количество энергии.
Поэтому я и спросил про ваше видение работы лазера без привлечения квантовой теории. Я не понимаю даже примерно каким оно может быть.
Справедливости ради, спектральные плотности научились считать классикой годах так в 50х
Это если рассматривать идеальную круглую частице в вакууме, а не группу частиц, где средняя по больнице частица пересечь барьер не может, а отдельная шустрая частица — может.
Как тогда можно объяснить слияние ядер дейтерия? Согласно закону Кулона, чем частицы ближе, тем больше сила отталкивания. Эта сила создаёт потенциальный барьер, причём он с классической точки зрения непреодолим вообще никак. Никакая отдельная шустрая частица не преодалеет его. Частицы приближаются -> сила растёт -> частицы должны отдаляться. В итоге, должно установиться равновесие между давлением и отталкиванием. Но увы, дейтерий превращается в гелий и звёзды светят вам назло.
Там как бы 4 силы действует, а не только электрическая.
Чтобы не угадывать, что вы имели ввиду, спрошу — какие именно?
То есть слабое и сильное взаимодействие, которые есть квантовые теории, намного более странные для обывательского опыта и куда более сложные математически вы принимаете, а квантовую механику с одной простой формулой — нет? Или принимаете, но когда это удобно?
Давайте так — если слабое и сильное взаимодействие в вашей физической картине мира есть — то опишите их как вы видите, но без квантовой механики, с классической точки зрения.
Вам прям медаль за невнимательное чтение вики.
Я тоже читал эти статьи. Там прямым текстом говорится:
Юкава предложил назвать поле, из-за которого осуществляется сильное взаимодействие, мезотронным, и, соответственно, квант этого поля именовать…
Кроме того, оно напоминает уравнение Клейна — Гордона, которое в релятивистской квантовой механике описывает волновую функцию бесспиновой частицы (бозона)
Сплошные кванты, которые вы не приемлете. Как без квантовой теории и обмена виртуальными частицами объяснить сильное взаимодействие? А слабое? Или тоже ссылку сейчас кинете? Ну так там тоже кванты, и все эти теории без базы в виде квантмеха не работают.
Потому что одинаковая амплитуда доходит до каждой точки экрана. Или вы хотите сказать, что свет устаёт?!?
Вам стоит ознакомиться с такими понятиями как плотность и плотность потока. Тогда неднородность пятна в случае незатухающих сферических волн сразу станет очевидной.
Тут речь про вот эти картинки: iopscience.iop.org/article/10.1088/1367-2630/15/3/033018/pdf
В статье прямым текстом написана причина неидеальной видимости:
The main reason for the drop in visibility between the detection slit and MCP detector(figure S2a and b) was the increase in detection resolution. The MCP detector and camera setup had a resolution of 238.2±6.6μm. This was determined by fitting the individual electron detection events and determining the appropriate detection resolution.
Там-же описаны проблемы измерения и в случае использования простой щели для регистрации электронов.
технические решения, разработанные благодаря применению аппарата квантовой механики, прочно вошли в повседневную жизнь современного общества
Магнитно-Резонансная Томография, или МРТ кажется стала неотъемлемой частью нашей жизни. При этом ЯМР и эффект Зеемана это чисто квантовые вещи, связанный со снятием вырождения по магнитному квантовому числу во внешем поле — классическая физика не способна объяснить их полностю. Это далеко не единственная, но наверное самая заметная простому обывателю чисто "квантовая" вещь.
Википедия говорит, что простой эффект Зеемана вполне описывается классической физикой. А ЯМР основан на ещё более простом эффекте.
Однако в описании ЯМР используется неквантовая модель атома, где момент (спин) образуется вращением.
P.S. Там же, в «объяснении» на которое вы ссылаетесь написано «Угловой момент и магнитный момент ядра квантованы». Давно в классической модели появилось квантование? Вы сами то ссылку до конца смотрели, прежде чем отправлять?
классические уравнения Максвелла, которые, в том числе, говорят нам, что любой заряд, движущийся с ускорением излучает.
Какое конкретно уравнение это утверждает? А Луна светится тоже потому, что вращается вокруг Земли с ускорением?
Излучение электромагнитных волн. Электромагнитные волны излучаются колеблющимися зарядами. При этом существенно, что скорость движения таких зарядов меняется со временем, т. е. что они движутся с ускорением. Наличие ускорения у движущихся зарядов — главное условие излучения ими электромагнитных волн.
В этом учебнике написана очевидная глупость. Но вы так и не ответили на мои вопросы.
Ну так 4-е уравнение. Переменное электрическое поле генерирует магнитное. Переменное магнитное — электрическое. Вот решение, которое даёт эм-волну — https://phys.spbu.ru/content/File/Library/studentlectures/Krylov/Gos_Ekzam-13-14-4.pdf
Далее, волна переносит энергию? Очевидно, что да. Откуда энергия берётся? Из ускоренной заряженной частицы. Ведь если бы частица двигалась равномерно, то в её СО поля были бы постоянные, а не переменные.
Переменное электрическое поле генерирует магнитное. Переменное магнитное — электрическое.
Откуда у вас взялось переменное магнитное поле?
Далее, волна
Изменение поля — ещё не волна. Колебания на этом масштабе взаимокомпенсируются.
Наличие ускорения у движущихся зарядов — главное условие излучения ими электромагнитных волн
вот это мне не очень понятно, а я бы хотел разобраться. Когда излучается волна? как только ускорение поменялось? А если оно продолжает меняться непрерывно? Как часто оно испускает фотоны? Или такого не бывает, а все изменения дискретны? Прошел квант времени — излучился очередной фотон? Следующий вопрос, частицы вещества все время колеблются. Иногда вещество состоит из ионов, они колеблются — значит должны излучать. Но если даже это нейтрально заряженные атомы, внутри у них есть ядро, которое колеблется вместе с ним. По этой причине все тела излучают свет?
2. Да, именно по этой причине. Точнее почти по этой. Тепловое излучение твердого тела частично можно объяснить колебаниями атомов решетки, можно условно сказать, что температура тела это и есть колебания (повторюсь — условно). Полное объяснение теплового излучения более сложное и уже требует квант мех.
где электроны движутся по кругу под действием магнитного поля и излучают фотоны
Всё-таки, как часто они излучают фотоны? В циклотроне скорость частицы, я так понимаю, меняется непрерывно?
Полное объяснение теплового излучения более сложное и уже требует квант мех
Вы имеете ввиду формулу Планка? Тогда почему именно твердого? Понятие температуры вроде не привязано к агрегатному состоянию.
2. Для меня всегда было проще понимать именно твердое тело, там можно и правда считать, что атомы колеблются вокруг узлов решетки. Все упорядочено. А так конечно агрегатное состояние не важно.
… где момент (спин) образуется вращением.
Принимать спин за реальное вращение по своей сути то же самое, что в КХД считать буд-то кварки действительно «разноцветные». Это не более чем абстрактная степень свободы для частиц, с использованием бытовой терминологии.
Иначе, не ровен час, можно договориться, что некоторые элементарные частицы просто очаровательно пахнут и просто прелестны :)
А вы не читайте советских газет перед едой. Изучайте разные источники.
Вот в английской вики:
All nucleons, that is neutrons and protons, composing any atomic nucleus, have the intrinsic quantum property of spin, an intrinsic angular momentum analogous to the classical angular momentum of a spinning sphere.
Внимание на слово analogous. Не тождественно равно, не ===, а аналог. Поищите ЯМР в гугле, и в каждой ссылке будет упоминание спина — чисто квантового явления. И везде говорится о спине, как об аналоге углового момента, а не о тождественно равного ему явления.
Да и вообще, идя по пути классической физики, вам сперва надо объяснить, как устроен атом, чтобы говорить о более сложных эффектах. А то у вас вроде эффект Зеемана описывается классической физикой, а в то же время, эта самая классическая физика не может предсказать спектр атомов.
Спасибо за интересную статью.
В случае с одной волновой функцией, чтобы найти вероятность взаимодействия частицы в точке x_j мы находим произведение j-тых компонент бра и кет вектора
Было бы хорошо дать краткое определение понятий "бра" и "кет" (либо привести ссылки).
Когда учитель физики заболел, его подменил физрук. Но он честно признаётся детям, что квантовую математику никто в школе не понимает. Настала пора учителя математики возвращаться, но дети уже друг другу рассказывают на том уровне, что никто в школе это и не доложен понимать, просто надо повторять за физруком, не обращая внимания и повторяя его ошибки.
Учителю физики будет трудно сначала всё-таки убедить детей, что понять, когда применишь силы — ну, физические, а умственные — то понять возможно. Но сил нету, а у физрука только физические силы, остальные привыкли слушать, а не думать.
Хуже всего тем школам, где физрук всегда вёл физику и по другому не бывает. Там дети даже немножко гордятся своей тупостью. Впрочем, физрук лучше, чем никого.
Хорошая статья, красивые слайды, поздравляю. В моём творчестве буду за вами в этом тянуться.
наличие интерференционной картины зависит от того, считывает ли кто-нибудь показания датчика
Это как? Я так понимаю, что любой датчик в процессе измерения взаимодействует с объектом и соответственно все нарушает/разрушает. А смотрит кто-нибудь на стрелку осциллографа или нет это уже дело десятое.
Здесь очень сложный вопрос «что есть датчик», потому что внутри там всё равно работает какой-то квантовый процесс, и сам датчик может перейти в запутанное состояние с объектом измерения (здесь — электроном) и таким образом оказаться в смеси двух квантовых состояний «электрон пролетел» и «электрон не пролетел». И коллапс волновой функции датчика произойдёт когда-нибудь потом, если кто-то решит узнать, что же там измерилось.
Коллапс волновой функции- это реальное физическое явление, чтобы говорить, что он произойдет? Или это условное обозначение?
Меня смущает использование местоимения «кто», а не «что» в физике.
Вот так вот насмотрятся научпопа и потом начинают путать субъективную модель мира и объективную реальность. Из того, что вы не знаете моего имени, не следует, что оно недетерминировано. Хотя волновая функция вашего представления о моём имени безусловно схлопнется, когда загляните ко мне в профиль.
В мобильной версии какой то баг, из-за которого все формулы в тексте обрамлены в $inline$
Видно, что человек интересуется темой, читает неплохие источники, но понимает далеко не все. Это в общем нормально. Большинство из нас такие. И квантовая теория действительно сложная и контринтуитивная. И по многим проблемам ее интерпретации вроде как нет единства среди специалистов.
Но здесь намешано в одну кучу много всего, по верхам, причем что-то более-менее правильно, а что-то совсем неверно. И попытки аналогий не делают на мой взгляд тему понятнее, а местами притянуты за уши. Автор молодец, что пишет — фиксировать свое понимание чего-бы то ни было в письменной форме очень полезно. Но читать это тем, кто не понимает квантовой механики и надеется понять, по-моему, не стоит.
Я не специалист, хотя заканчивал физфак (давно) и не стал бы лезть со своими оценками, но никто из профессионалов пока в комментариях не отметился. А все, кто комментируют, либо хвалят, либо обсуждают отдельные детали. В результате, у мимопроходящего любопытствующего может сложиться мнение, что это годное введение в тему. К сожалению, это не так.
Возможно, для каких-то других целей статья окажется полезной. Дискуссию в комментариях она, по крайней мере, вызвала. :)
Вопрос к таковым: что происходит с волновой функцией в момент измерения, например вот тут? youtu.be/p7bzE1E5PMY?t=328
Там же диктор говорит — коллапс и эффект наблюдателя. И это все хорошо гуглится. А уж как понимать, это дело вкуса: можно как математические конструкты, можно как таинство растущее из объективной случайности, или же вообще — ансамбли, корпускулы в квантовом поле или one-hot вектора
Ок, раскрою вопрос.
Возможно, наивный.
Возьмем описание gaussian wave packet (который показан в видео) например отсюда: people.physics.tamu.edu/valery/Gaussian%20wave%20packet.pdf
После некоторых преобразований у нас получается (12), волновая функция от времени и положения, psi(x, t), из которой можно вычислить вероятность нахождения частицы в x в момент времени t.
Теперь мы, как в видео, выполняем измерение, которое нам возвращает положительный результат: частица находится в интервале x = [x_left...x_right], т.е., интеграл квадрата модуля ВФ от x_left до x_right = 1.
Вопрос в следующем: как теперь выглядит ВФ (12)? Возможно, в момент измерения ее можно представить как piecewise («кусочно заданной»?) функцией, типа ВФ = (12) for x in [x_left...x_right] else 0, и нормализовать, но что тогда делать с условием непрерывности по первой производной? Как ее сгладить по краям, и как это выглядит математически?
Это уже хороший вопрос, а не "что происходит с волновой функцией на видео".
Формально, вы можете решить УШ для вашей гауссовой функции включив взаимодействие с полем некого потенциала явно с самого начала эксперимента
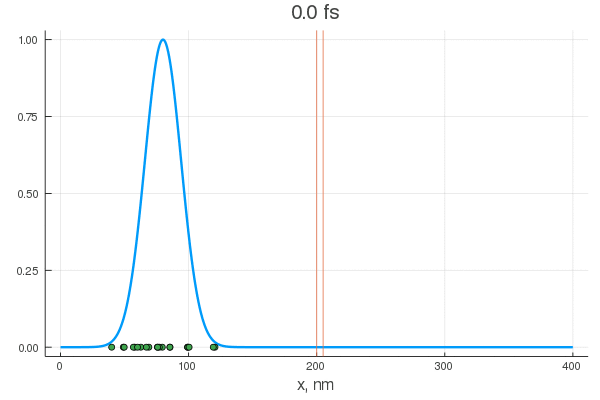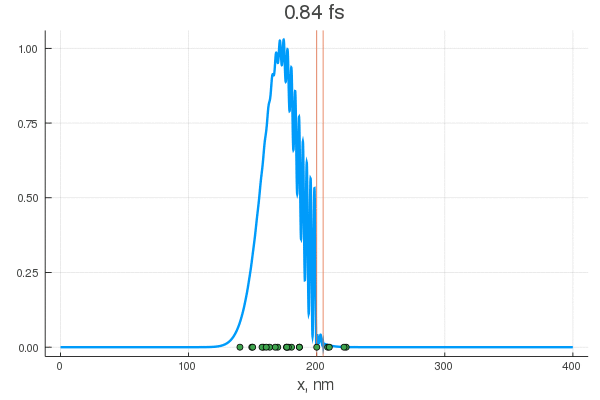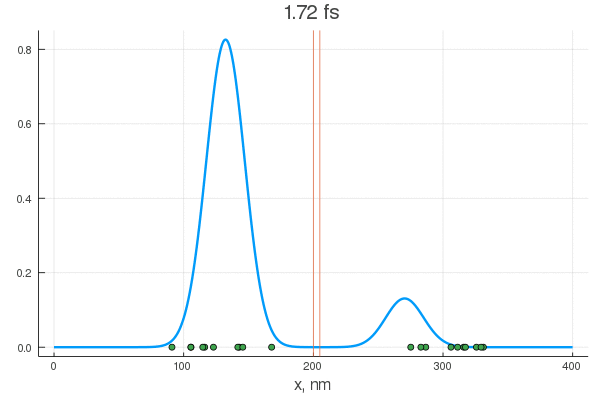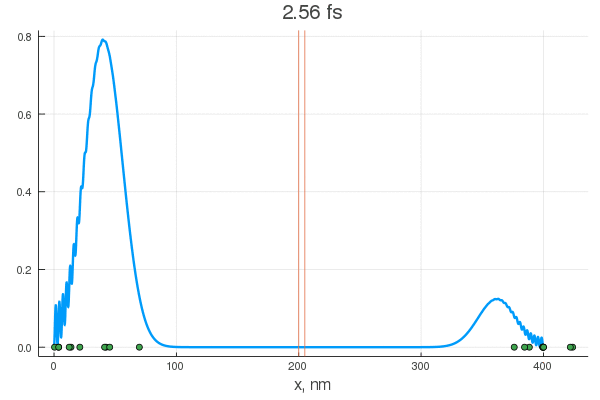
Но ничто не мешает включить его в произвольный момент (100-120 шаг)
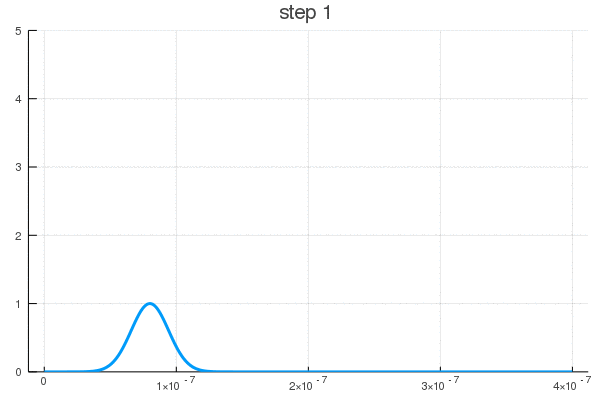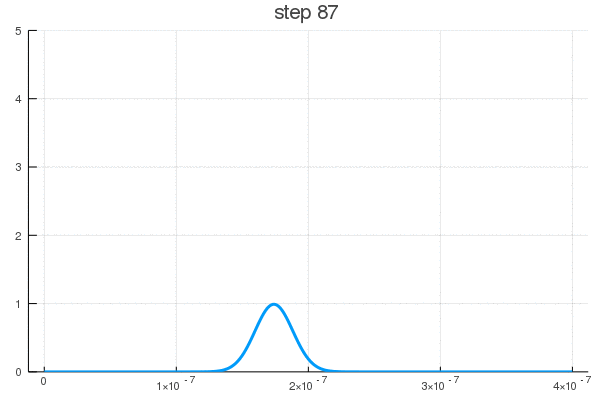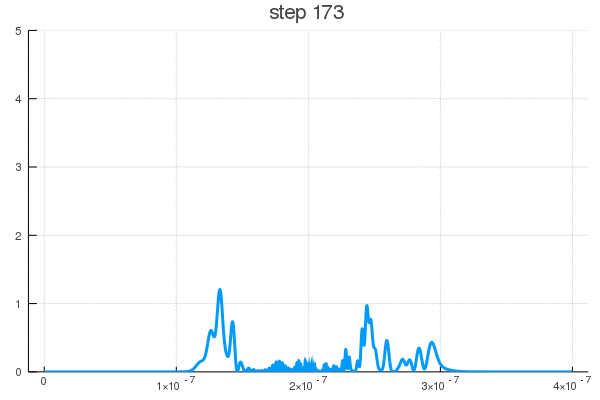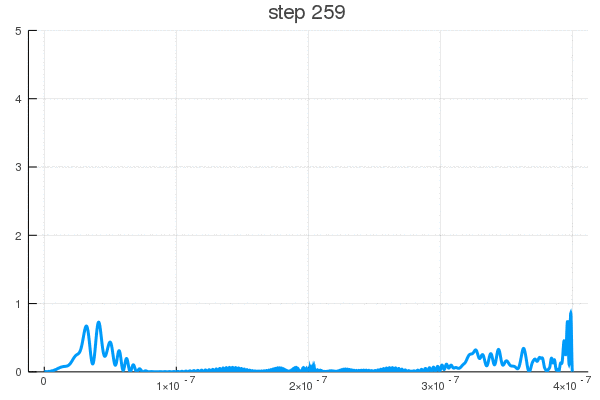
Можно постараться минимизировать время взаимодействия (100-105 шаг)
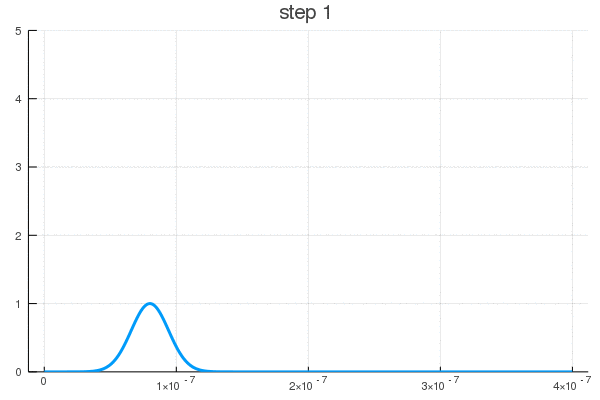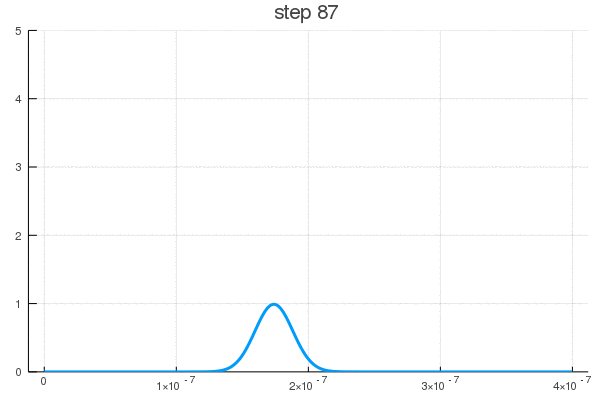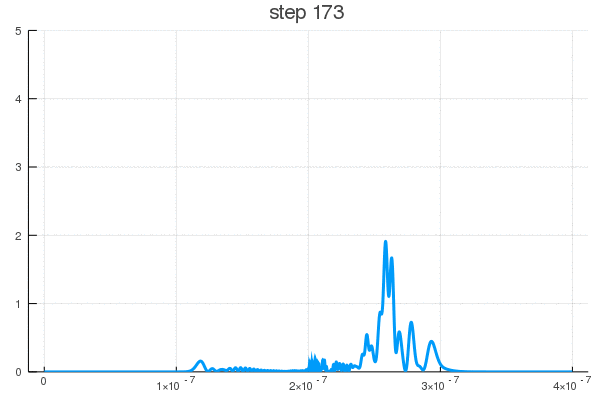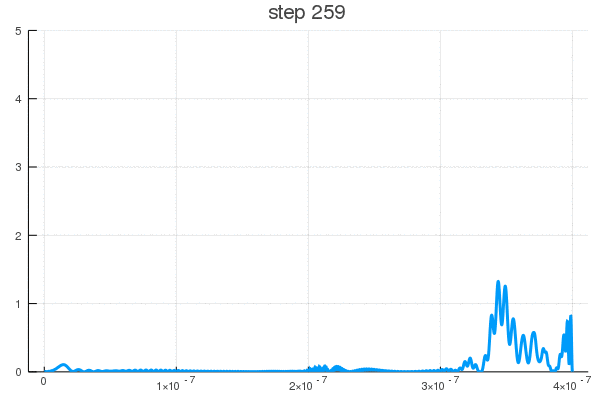
Как видите, поведение ВФ нетривиально даже для одномерной задачи с прямоугольным потенциалом. В реальности же установка может быть представлена, к примеру, некой эмульсией, меняющей цвет или фосфорисцирующей при попадании частицы. Да мы узнаем координату, но ценой вот такого разрушения чистой квантовой системы, после ее взаимодействия со сложными полями прибора, что запускают цепную реакцию изменений выходящих на масштаб, приемлемый для наших органов восприятия.
p.s. у меня шаг = сотой фемтосекунды — экспериментаторы за такое могут и надавать по лицу микроскопом
А как еще проще изобразить взаимодействие квантовой системы с чем-то? На видео была одномерная задача без интерференций и запутываний, вот мы и рассматриваем простейший случай. Так-то да, там будет и наведение поля частиц эмульсии и прочие радости взаимодействия химической реакции. Ну и использовать коллапс я наверное больше не буду в объяснениях: прельстила бомовская механика с ее проблемой многих частиц, а так да, можно проще сказать, что как только врубили детектор функция схлопнулась, и никакие вторичные волны не разбегаются
А как еще проще изобразить взаимодействие квантовой системы с чем-то?С измерителем? Никак. Как коллапс. Или как запутывание. Но точно не как барьер. Это создает неверное представление, что ВФ после измерения имеет ненулевую вероятность где-то кроме экрана и даже продолжает эволюцию. Это не так. С точки зрения наблюдателя в любой интерпретации частица уже измерена, и дальше не эволюционирует.
Ну и использовать коллапс я наверное больше не буду в объяснениях: прельстила бомовская механика с ее проблемой многих частицНу тогда уж надо объяснять в рамках бомовской механики, что явно не согласуется с гифками выше.
Ладушки, возможно я не очень последователен. В гифках я заострялся именно на воздействии на частицу нечтом извне — чем-то, что разбивает ВФ пакет на кусочки. Про измерение же сказал, что это сложно, многочастично и труднорисовательно. На видео же диктор говорит именно про измерение, просто там коллапс локализуют в широкий прибор просто обрезав пакет, и потому они рисуют ВФ дальше по времени, не заморачиваясь, на то как это вообще осуществлять.
С измерителем? Никак. Как коллапс. Или как запутывание.А нельзя рассматривать редукцию ВФ, как идеализацию декогеренции? Где-то читал про это. Если провести аналогию, то изменения уровня ттл-логики отрисовывают на диаграммах идеальными прямоугольными импульсами, но если напряжение померить точным прибором, то увидим небольшие шумы, переходные процессы, конечное время перехода из одного состояния в другое, т.е. прямоугольники это идеализация.
Сейчас декогеренция — общепринятая концепция, и она естественным образом включается как необходимый механизм, например, в многомировой интерпретации.
А вот квантовый дарвинизм же как раз пытается объяснить получение конкретного исхода из суперпозиции в ходе декогеренции. Надо критику почитать будет
ММИ, из-за непротиворечивости, имеет право на существование, но больше создает видимость объяснения, т.к. никаких специфических эвристик, предсказаний не предлагает. Это все равно, что мы задались бы вопросом — почему скорость света именно 300 000 км/сек, а не другая? А потому что существуют другие вселенные в которых скорость 200 000, 400 000, и тд, непротиворечивое объяснение, нам просто выпало, что у нас именно такая) В ТС нечто подобное пытаются проделать, с известными результатами.
В полном объеме селекцию состояний в кв. измерениях может объяснить новый уровень фундаментальной физической теории, кот. возможно примирит кванты с гравитацией, объяснит темные сущности, происхождение и эволюцию Вселенной, и, главное, будет делать проверяемые экспериментами и наблюдениями предсказания в больших объемах, чем существующие теории. Но это будет связано не только с непротиворечивостью описания в этой новой теории, но и введением дополнительных запретов, типа предельности ск. света, или ограничений типа законов сохранения, т.е. дальнейшего роста связности состояний физических систем. Возможно введение дополнительных независимых степеней свободы, типа спина. Связность, кстати, в немалой степени обеспечивается уже на биологическом уровне, например, в виде константности восприятия. Физические ограничения продолжение и расширение этой тенденции на новом уровне. Вероятно многое будет определяться конечностью или бесконечностью сущности, кот. мы называем физической реальностью, ее закрытостью, или принципиальной открытостью. Если бесконечна, то теряет смысл само противопоставление случайности и детерминизма в описании ее поведения, вплоть до того, что в некоторых случаях в нем можно будет усмотреть некий умысел)
Пока же приходится довольствоваться статистическими предсказаниями результатов кв. измерений.
ММИ, из-за непротиворечивости, имеет право на существование, но больше создает видимость объяснения, т.к. никаких специфических эвристик, предсказаний не предлагает.Мне кажется, это не совсем верно. ММИ представляет ровно те же предсказания, что и квантовая механика. Можно сказать, что в настоящий момент квантовая механика == ММИ. Поэтому мы постоянно проверяем ММИ в наших экспериментах и пользуемся ее предсказаниями. А вот другие интерпретации добавляют новые постулаты или механизмы, и требуют дополнительных проверок, и пока нет другой непротиворечивой интерпретации. Да, в ММИ есть вопросы философского толка о том, как нам думать об этих других мирах. Но это не фундаментально физический вопрос, а скорее вопрос нашего восприятия. Поэтому, в отличие от других интерпретаций, ММИ описывает мир полностью и непротиворечиво, но мы не до конца понимаем, как об этом говорить в привычных нам бытовых терминах.
А с остальным согласен.
Можно получать данные из-за границ неизвестности, а потом ваши данные будут переданы за другую границу, держащую до поры вас для неё неизвестным. При этом при переходе этих границ выбор случаен. Многомировая интерпретация говорит, что выбор случаен, потому что каждый вариант реален. А полный детерминизм говорит, что выбор варианта не зависит ни от чего, и может быть просто быть где-то записан отдельно. Сами границы — это отдалённость выбора до момента когда он срабатывает, и отдалённость можно растягивать.
На проблеме различия этих интерпретаций можно выехать только в две области: 1. Понять, что разговор идёт о том, что от нас не зависит, и значит, это глупость. 2. Зависимость есть, но она имеет характер обратной зависимости. То есть, обе стороны влияния реальности, сама реальность, чем-то сгенерирована третьим. Материалисты в шоке.
Из комбинации интерпретаций один на один стало опять один на один, но это уже другие.
Многомировая интерпретация говорит, что выбор случаен, потому что каждый вариант реален.Вообще говоря, ММИ полностью детерминистична. Нет «случайного» выбора. Строго говоря, даже случайность как понятие не определена в ММИ. Поэтому я не очень понимаю различия.
А полный детерминизм говорит, что выбор варианта не зависит ни от чего, и может быть просто быть где-то записан отдельно.Он и записан — в волновой функции.
Мне кажется, это не совсем верно. ММИ представляет ровно те же предсказания, что и квантовая механика. Можно сказать, что в настоящий момент квантовая механика == ММИ.Не сказать, что отвергаю такое объяснение полностью, но оно не является интерпретацией, и оно не приоритетное. Если читали этот перевод и мои коменты к нему, то в них анонсировал статью в продолжении темы субъективных состояний в физике в контексте истории, философии и когнитивной науки. В общем и целом она готова, нужно доработать детали, и что-то сделать с объемом) Поэтому приведу цитату из нее связанную с ММИ, и собственным пониманием проблемы.
Интерпретация Эверетта начала получать признание только после того, как стараниями других физиков, в частности Де Витта (De Witt B. (1970, 1973)), была своеобразным образом объективирована путем обобщения на состояние всей Вселенной, а не только связанной с процедурой измерения производимой наблюдателем. Ветвления ВФ были связаны с ветвлениями независимых миров, а не с ветвлениями состояний сознания наблюдателя. Соответственно эта интерпретация получила новое название Многомировой. В таком виде она нашла достаточно широкое признание среди физиков. Однако сказать, что в работах связанных с тематикой ММИ отсылки к роли наблюдателя и его сознания прекратились нельзя, как пример эта работа. Цитаты:
Теория определена таким образом, что нигде прямо не ссылается на наблюдателей, но, чтобы понимать, почему Вселенная такая, как мы ее воспринимаем, нужно обратиться к проблемам связанным с наблюдателем – прежде всего, нам нужно понять наше восприятие вероятности.
Описываем ли мы квантовый универсум в терминах множества глобальных миров или в терминах более локализованных событий, мы непременно используем наше интуитивное понимание локальной и количественно-определенной (для некоторых наблюдаемых) пространственной области — не в математическом смысле, а в концептуальном понимании, и осознания нашего собственного места в ней.Этот бакграунд скрытый от разработчиков физических теорий, который является отправным пунктом разработки, и одновременно ее внутренним ограничителем, аналогичный поискам оснований КМ Бором, является прямой отсылкой к теме современных когнитивных исследований. Но эта интересная тема для отдельной публикации, в частности, в контексте современных поисков Новой физики.
Считается, что экспериментальная проверка ММИ не осуществима из-за отсутствия влияния между мирами (хотя есть модификации теории с такой возможностью). Но установление природы измерения, в контексте восприятия, не сводится только к физике. Оно имеет также когнитивную составляющую, которая может дать подсказку к направлению поисков, связанных с исключением вариантов объяснения коллапса. В результате такого исключения останется возможной ММИ, в которой коллапс не происходит. Либо дожидаемся чуда — теорию нового поколения, которая ответит на все наши вопросы, и по традиции поставит новые) Как ОТО ответила на вопрос связанный с теорией тяготения Ньютона — что такое гравитация? Но возникли новые. Как она квантуется? Или, что такое само пространство-время?
Не сказать, что отвергаю такое объяснение полностью, но оно не является интерпретацией, и оно не приоритетное.Ну да, а строго говоря ММИ и не интерпретация в том же смысле как копенгагенская, скажем, т.к. она не добавляет ничего нового квантам. И я не уверен, что вы имеете в виду под «не приоритетное объяснение».
Я согласен, что в ММИ есть сложность в объяснении субъективного наблюдения вероятностей в полностью детерминистичной теории. Но со времен Эверетта мы довольно далеко продвинулись в ММИ, и есть несколько вариантов, которые объясняют это.
Мы с вами уже это обсуждали, наверное, не имеет смысл повторяться, но я не уверен, что когнитивная составляющая должна играть роль в теории. Нам нужно объяснить наше воприятие классического мира, но это не обязательно завязано на сознание как таковое.
И я не уверен, что вы имеете в виду под «не приоритетное объяснение».Исключительно в списке приоритетов объяснений в моем понимании. В курсе, что как минимум треть физиков, если не больше, по разным оценкам, поддерживает ММИ, как основное.
но я не уверен, что когнитивная составляющая должна играть роль в теорииВ физической теории нет, но вот в способности их создавать может. Это разные уровни. Представьте ситуацию — лет через 50 все также бурно обсуждают и создают варианты ТС и интерпретаций КМ. Все больше теоретиков занято этим, от публикаций по этой теме гнобится интернет) от мат. затрат на новые коллайдеры и зп теоретиков страдают бюджеты стран), и тп. Считаете так и должно быть? Конечно, представил развитие в абсурдистском пределе. Но современная ситуация все больше начинает походить на него, есть некоторые показатели. Заставляет задуматься о причинах. Возможно проблема не только в объекте познания, его чрезвычайной сложности, а и в субъекте его производящим. И хорошо было бы, что я ошибаюсь, проблемы с созданием новой фундаментальной теорией будут благополучно решены, нобелевки выданы, а прогрессивное человечество получит новые технологии)
Но современная ситуация все больше начинает походить на него, есть некоторые показатели.Интерпретации КМ вообще мало кто обсуждает, относительно. Есть, конечно, перекосы, но учитывая, что наука это такой мизерный сектор финансовый и информационный, я не вижу вообще проблемы.
Возможно проблема не только в объекте познания, его чрезвычайной сложности, а и в субъекте его производящим.Возможно. Это, конечно, интересный и важный вопрос, и хоть я и не думаю, что это будет играть важную роль в конце концов, это моя интуиция. Это однозначно заслуживает обсуждения и дальнейшего исследования.
я не уверен, что когнитивная составляющая должна играть роль в теории.
Вряд ли это возможно, если учесть, что любая теория это продукт когнитивной составляющей.
Нам нужно объяснить наше воприятие классического мира, но это не обязательно завязано на сознание как таковое.
Не уверен, что человечество уже объяснило себе, что такое "объяснить"… Пока что слишком часто встречаются логически неверные умозаключения вида "мы установили соответствие между А и Б, следовательно нет никакого Б, потому что Б это А". Тем временем, соответствие это всего-лишь соответствие, а никакое не объяснение, и уж, тем более, не тождество.
Без восприятия теряет смысл понятие сознания. Без сознания теряет смысл понятие восприятия (по крайней мере, такого, о котором мы можем говорить осмысленно). И то, и другое имеет когнитивный характер. Подозреваю, что сформулировать теорию (любую, не обязательно физическую), от которой ожидается объяснение термина, но без использования самого термина, вряд ли возможно. Как минимум должно быть утверждение тождества, где слева будет термин, а справа — определённая дескрипция в других терминах. Кстати, интересным свойством теории, которая по-настоящему сумеет объяснить сознание и восприятие как не-сознание и не-восприятие, должен стать такой вау-эффект наступления понимания, при котором изучающий лишается и сознания, и восприятия. :)
Вряд ли это возможно, если учесть, что любая теория это продукт когнитивной составляющей.Я имею в виду, что может существовать теория, которая описывает вселенную и сознание. Нет фундаментальных препятствий созданию такой теории.
Пока что слишком часто встречаются логически неверные умозаключения вида «мы установили соответствие между А и Б, следовательно нет никакого Б, потому что Б это А».Мне кажется, в научном сообществе такое встречается редко, это основа научного метода.
Без восприятия теряет смысл понятие сознания. Без сознания теряет смысл понятие восприятия (по крайней мере, такого, о котором мы можем говорить осмысленно).Не знаю, я не соглашусь тут. Восприятие вполне может быть без сознания. Т.е. восприятие однозначно может быть описано физически без привлечения сознания. А сознание как эмерджентый феномен возникает на высшем уровне.
Восприятие вполне может быть без сознания.
Если говорить о реальном восприятии, т.е., о том, которое знакомо каждому из нас непосредственно, а не исключительно теоретически, то какой акт восприятия мы можем взять, как пример бессознательного? Даже восприятие во сне обладает как минимум той мерой сознания, при которой в сыром чувственном потоке различаются объекты и паттерны. Кроме того, с аналитической стороны: для того, чтобы хоть что-то различать в восприятии, нужно хоть какое-то сознание. Если предположить бессознательное восприятие, то это такое восприятие, в котором ничего не различимо. Есть ли у нас опыт такого восприятия? Можно ли, вообще, называть такое неразличимое нечто восприятием, и если да, то по какому критерию?
Восприятие вполне может быть без сознания. Т.е. восприятие однозначно может быть описано физически без привлечения сознания.
Может быть и может быть описано это принципиально разные концепции. Если всё может быть описано через последовательность нулей и единиц, из этого не следует даже намёка на то, что всё может быть нулями и единицами. Описание явления А в терминах Б это, по сути, и есть то самое установление соответствия (подтверждающееся или не подтверждающееся экспериментально), которое не есть тождество.
Вообще же, ни известное нам непосредственно сознание, ни восприятие — реальные сознание и восприятие — в своей актуальной действительности (в процессе субъективного сознательного переживания) не являются физическими феноменами. Лучшее, что может сделать физика — попытаться эмпирически установить те или иные соответствия между психическим и физическим, но не более, т.к. речь о радикально разных типах явлений. В определённых кругах есть такое понимание, особенно, на фоне непрекращающихся провалов всех редуктивных подходов. Поэтому существуют менее радикальные программы физикализма, например — супервентность.
А сознание как эмерджентый феномен возникает на высшем уровне.
Вряд ли можно говорить уверенно об эмерджентности без демонстрации её механизма. Насколько мне известно, это красивая филсофская концепция, но не особо проработанная, по крайней мере не по отношению к сознанию. Кроме того, насколько я понимаю эту концепцию, хоть она и предполагает возникновение свойств, не редуцирующихся к сумме базовых свойств элементов системы, но, тем не менее, она не предполагает возникновение свойств, превращающих систему в нечто радикально другого типа. Например, песок это песчинки, у совокупности которых при достаточно большом количестве появляются эмерджентные свойства. Но песок всё равно продолжает состоять из песчинок. Сознание и восприятие это вещи другой категории. Нельзя утверждать, что они состоят из клеток нервной системы, полностью не лишая эти понятия смысла их непосредственной реальности (т.е., безусловной истинности).
Имхо, привлечение таких терминов, как "эмерджентность" и "высший уровень", ничего не добавляет к действительному пониманию предмета, когда речь идёт о таких фундаментальных непосредственных реальностях, как сознание и восприятие.
Если говорить о реальном восприятии, т.е., о том, которое знакомо каждому из нас непосредственно, а не исключительно теоретически, то какой акт восприятия мы можем взять, как пример бессознательного?Я подхожу к этому с натуралистичной и редукционистской позиции. Восприятие — атрибут любого живого, включая всякие микробов. Это буквально обработка входного сигнала в некоторую реакцию. При этом сознание там не при чем. Поэтому восприятие можно описать полностью.
Вообще же, ни известное нам непосредственно сознание, ни восприятие — реальные сознание и восприятие — в своей актуальной действительности (в процессе субъективного сознательного переживания) не являются физическими феноменами.Это сильное заявление. Я считаю, что они являются физическими феноменами.
Лучшее, что может сделать физика — попытаться эмпирически установить те или иные соответствия между психическим и физическим, но не более, т.к. речь о радикально разных типах явлений.Это тоже не очевидно. Я не вижу ограничений описания психического через физику (в конечном итоге).
Поэтому существуют менее радикальные программы физикализма, например — супервентность.Да, и я придерживаюсь редукционизма.
Вряд ли можно говорить уверенно об эмерджентности без демонстрации её механизма. НасколькоСовершенно согласен. Мы понятия не имеем, на самом деле. В рамках парадигмы, в которой я, как физик, оперирую, сознание может быть только эмерджентым феноменом.
Нельзя утверждать, что они состоят из клеток нервной системы, полностью не лишая эти понятия смысла их непосредственной реальности (т.е., безусловной истинности).А можно привести другой пример: движение частиц и их статистика проявляются как эмерджентый феномен — температура. Составляющие (частицы) не обладают этим феноменом даже близко. Точно так же нейроны не обладают сознанием, но их взаимодействие приводит возникновению качественной иной сущности — сознанию. Тем не менее, как мы можем объяснить температуру как некий коллективный эффект, так мы сможем объяснить (и строго описать) сознание как коллективный эффект.
речь идёт о таких фундаментальных непосредственных реальностях, как сознание и восприятие.Я не считаю, что сознание и восприятие обладают независимой реальностью. Конечно, есть и другие точки зрения, некоторые вообще считают, что сознание принципиально находится вне научной парадигмы.
Это сильное заявление. Я считаю, что они являются физическими феноменами.
То, что они являются физическими феноменами — не менее сильное заявление. Впрочем, выше Вы отметили, что исходите из философских позиций редукционизма, поэтому причина Вашего заявления понятна. Не совсем понятны причины принятия редукционизма.
Вы вот говорите о бритве Оккама, но это обоюдоострый предмет… :) Человек включает её (если это вообще происходит) только после определённого периода жизни, в течение которого он накапливал сущности бесконтрольно. Но при включении бритвы, её можно использовать по-разному. Например, можно зафиксировать определённую, более-менее уже знакомую, метафизическую картину (скажем, физикализм), и отсечь всё остальное. Получится физический редукционизм.
Или можно отсечь всю стихийно накопившуюся онтологию, чтобы выстроить новую с нуля, критически — без лишних сущностей. При таком подходе как раз формы материализма и физикализма окажутся лишними сущностями. (Без ущерба для самой физики, кстати.)
Если, с помощью бритвы Оккама, отвлечься от навязываемых обществом позиций, то восстановление онтологии рационально начать с вопроса "что мы имеем?". Точнее, что конкретно я имею, т.к. "мы" это уже абстракция, каждому субъекту дано только его "я". Окажется, что есть ряд эмпирических данностей, отрицать наличие которых равнозначно отрицанию собственного существования. Отрицание собственного существования равнозначно отрицанию своего текущего опыта, что явно не рационально — никакая наука не смогла бы существовать, если бы каждый учёный отрицал свой опыт (опыт наблюдения показаний приборов, например). Это может нравиться или не нравиться, но личное субъективное существование — это первично доступная человеку реальность. И, кстати, единственная, т.к. контакт с гипотетической (на этом этапе работы с бритвой) объективной реальностью осуществляется эксклюзивно через субъективную. Что дальше? Ничего на самом деле не наблюдается человеком объективно. Но из наблюдений логически следует, что существует что-то вне субъективного. Это физический мир? Вряд ли, если говорить о физическом мире в общепринятом понимании. Дело вот в чём: то, что существует вне моего субъективного, либо существует в чьём-то субъективном, либо как-то иначе. То, что существует иначе (т.е., не субъективно), не может включать в себя никаких субъективных свойств типа ощущений, эмоций и, да, абстракций. Если что-то такое не-субъективное существует, то оно бесцветно, беззвучно, безпространственно и т.д. — все наши понятия, включая понятия о пространствах, исключаются из него. Физика определённо изучает не не-субъективное. Максимум — она пытается восстановить модели, по которым синхронизируются наши субъективные реальности. Причём довольно успешно с технологической точки зрения.
Теперь подсчитаем. В моей онтологии есть всего три сущности: субъективное, модель, нечто (не-субъективное). Существование "нечто" также устанавливается аналитически "от противного", но это другая тема. Достаточно сказать, что это область принципиально неисследуемого. О нём можно говорить только в категориях отрицания — любой утвердительный предикат это не о нём. Существование субъективного — это непосредственная реальность. В ней есть много чего интересного, но всё это явления психического характера. Модель — в той мере, в которой её детали становятся известны человеку, она становится частью субъективного. Т.е., сущности, по-сути, всего две.
На это, несомненно, любой материалист ответит, что он победил, т.к. у него сущность одна — материя. Это мнимое превосходство, т.к., во-первых, само это понятие бессодержательно, т.к. априори натягивается на всё и вся и потому ничего не может объяснить, его можно безболезненно "вынести за скобки" и ровным счётом ничего не потерять. Во-вторых, существование материи невозможно установить ни эмпирически, ни логически — ввиду бессодержательности понятия. Поэтому на деле физикалисты от физики постулируют большое количество разных сущностей, совершенно игнорируя бритву Оккама. Так что бритва Оккама это очень плохой аргумент с позиции физического редукционизма.
Я не считаю, что сознание и восприятие обладают независимой реальностью.
Я тоже так не считаю. Отсюда не следует физикализм. Впрочем, не исключено, что мы по-разному понимаем, что такое "обладать независимой реальностью".
Тем не менее, как мы можем объяснить температуру как некий коллективный эффект, так мы сможем объяснить (и строго описать) сознание как коллективный эффект.
Или не сможем. Пока, при всех усилиях, не смогли. И есть много причин считать, почему никогда не сможем.
Ну смотрите, в современной физике у нас нет вообще интуитивных компонент. Ни квантовая физика, ни физика частиц, ни теория относительности не интуитивны.
Наоборот. Всё, что кто-то понимает в физике, это то, что стало для него интуитивно ясным. Всего остального он не понимает. Интуитивно ясное не равнозначно легко понимаемому. Некоторые интуитивные ясности достигаются только через продолжительный опыт когнитивных усилий, и то не всеми. Да, физика теории относительности и физика квантовой механики отрицают обыденные интуиции. Но, повторюсь, они могут быть кому-то понятны лишь в той степени, в которой этим кем-то достигается интуитивная ясность об этих теориях. Нет интуитивной ясности — нет понимания.
Но пока у нас нет подтверждений этой гипотезы.
Вообще-то, есть. Во-первых, аналитически — из требования интуитивной ясности для понимания (т.о., и для объяснения). Во-вторых, эмпирически — адептами любых достаточно популярных теорий предпринимаются титанические усилия для того, чтобы у по-возможности максимальной аудитории была достигнута интуитивная ясность. Это касается не только физики, но и чисто абстрактных дисциплин, таких как, например, теория множеств и теория категорий.
Я ценю время, которое вы уделили для ответа, но, честно говоря, не готов к настолько развернутой и полноценной дискуссии — завал на работе, а для ответа на все потребуется много слов. Тем более что, кажется, наши с вами различия в мировоззрении слишком сильны, чтобы мы смогли провести дискуссию, полезную для обеих сторон. Прошу прощения.
Что Вы, никаких проблем. Я прекрасно понимаю, насколько низки шансы для взаимной продуктивности в таких разговорах. Для меня это удобная возможность пошлифовать мысли — в диалоге есть дополнительная мотивация делать это. С моей точки зрения разговор был продуктивным (вероятно, не вполне взаимно, сорри), так что спасибо.
P.S. По мировоззрению я идеалист — не очень (мягко скажем) распространённый в зените популярности материализма взгляд на вещи. Иногда чувствую себя как ситх в эпоху расцвета Республики и джедаев. :) Но ничего, относительно недавно ситхи идеалисты преобладали. Имхо, с дальнейшим развитием наук есть все шансы возвращения идеализма, обновлённого и тщательно обоснованного.
Я имею в виду, что может существовать теория, которая описывает вселенную и сознание. Нет фундаментальных препятствий созданию такой теории.
Тоже, кстати, тот ещё вопрос… Я убеждён, что любое настоящее объяснение, как и любое настоящее понимание, должно составляться из интуитивно ясных компонент. К интуитивно ясному относится всё качественное в нашем восприятии, включая эмоции и абстракции типа круга или числа. Да, некоторые вещи требуют определённой тренировки для достижения интуитивной ясности — для осваивания высокоуровневых абстракций надо много заниматься предметами типа логики и математики, для различения большого количества оттенков надо заниматься чем-то вроде рисования или живописи, и т.д.
Так вот, если предположить, что дано некоторое объяснение в терминах, о которых ни у кого нет интуитивной ясности, то каким образом это можно будет считать объяснением, а не бессмысленным набором слов или символов? Общепринятая сегодня практика объяснения конкретного через абстрактное тоже, кстати, вызывает вопросы, но в ней, по крайней мере, есть достаточно сильная интуитивная база, непонятки только с направлением вектора объяснений. С абстракциями тоже есть (правда, чисто техническая) проблема, т.к. чем сложнее и, простите за каламбур, абстрактнее абстракция — тем проще её понять некорректно бОльшим количеством способов. И вот, если любая наша теория, которая может что-то по-настоящему объяснить, должна апеллировать к нашей интуиции, то окажется, что объяснения любых физических теорий будут сводить объективную реальность к субъективным интуициям человеческого разума. Что, собственно, и происходит со всеми теориями, предлагающими ту или иную метафизическую картину.
Можно, конечно, предположить такую теорию, которая таким образом скомпонована из математического аппарата, что, не имея метафизической части, позволяет эффективно предсказывать результаты экспериментов. Как кто-то знаменито выразился "заткнись и считай". :) Только вряд ли можно будет утверждать, что такая теория что-то объясняет.
В общем, имхо, совсем не исключено, что мы таки имеем фундаментальное ограничение на возможность такого объяснения объективной реальности, которое бы полностью исключало субъективность нашей индивидуальной реальности. Собственно, очень похоже, что все термины объяснения, которые принципиально не имеют ясности в субъективной интуиции, для любого человека будут просто бессмысленным набором символов.
Я убеждён, что любое настоящее объяснение, как и любое настоящее понимание, должно составляться из интуитивно ясных компонент.Ну смотрите, в современной физике у нас нет вообще интуитивных компонент. Ни квантовая физика, ни физика частиц, ни теория относительности не интуитивны. Мне совершенно не очевидно, почему такое
В общем, имхо, совсем не исключено, что мы таки имеем фундаментальное ограничение на возможность такого объяснения объективной реальности, которое бы полностью исключало субъективность нашей индивидуальной реальности.Не исключено, конечно. Мы вообще много чего еще не знаем:) Но пока у нас нет подтверждений этой гипотезы. А пока их нет, я, например, предпочитаю пользоваться бритвой оккама и не добавлять сущностей, где не нужно.
Не, так не пойдет :-)
Мне тут пришло в голову, что правильно обрезать по значениям k-space, которые соответствуют скорости света => c * m / hbar. Как и саму исходную гауссиану, кстати.
В КМ вообще где-нибудь появляется скорость света?
Таки речь об наличии информации о пути частицы в «системе» (волновых функций?), а не обладании или нет ею экспериментаторами
At time T0 when D0 is triggered no interference appears, since the which-way information is contained in the system at that time. At time T1, which in the experiment is some nanoseconds later but could be in principle any time later,10 when D1/D2/D3/D4 are triggered, we find interference in the correlated subsets of past D0 records undergoing future erasure of the which-way information.
Вот только «конверты» должны быть защищены от декогеренции. То есть либо микроскопическими, либо макроскопическими, но всё равно экзотическими и при околонулевой температуре.
Квантовая механика соответствует механизму волн ещё больше, чем просто волны.
Например, если от двух источников в одно месте накладываются волны в противофазе, то в этом месте волны гасят друг друга. Но для материальных объектов в это место можно поставить столб, от которого пришлось бы отскакивать. И тогда получается интересный эффект: если два потока не различать, то в этом месте поток нулевой, отскакивать нечему. А если различать, то отдельная волна наткнётся на этот столб и поменяет направление. Это в физике работает математически: как оказалось, что инертная масса и масса гравитационная масса это одно и то же, так и оказалось, что знать о чём-то означает различать это, а прежде всего отличать от объективно неизвестного состояния, что приводит к перераспределению вероятностей.
Удивляться тут нечему, это надо просто понимать.
Второй вопрос — когда именно происходит разделение.
Вот представьте в одном месте вселенной датчик случайных чисел и он сгенерировал случайное число. От него во все стороны потекли «лучи различия» что вселенная разделяется на две. Кто пересечёт этот луч — попадает в одну из вселенных, и где-то есть информация в какую именно.
На другом конце вселенной датчик случайных чисел тоже выбрал число и от него во все стороны полетели «лучи различия». При попадании в такой луч тебе говорят что вселенная раздвоилась и уже могут сказать, в какой вариант ты попал.
Прикол в том, что если это обычные лучи, то при их пересечении оказывается перемножение два на два — четыре варианта вселенных. А если это сцепленные датчики — то они так накладываются, что останутся только связанные состояния. В итоге, будет две вселенной. То что датчики когда-то были сцеплены в одном месте уменьшает загадку, как же так получилось. Но удивляет тем, что сцепленность может сохраняться продолжительное время.
То есть, нету удалённого взаимодействия. Есть сохранение эффектов первоначального взаимодействие, с отложением проявленности.
И теперь осталось осознать, что источник того, в какой вселенной окажется любой объект вокруг датчиков вообще не связан с этим объектом. А значит, выбор происходит вне его времени. В этом смысле множественность миров и полный детерменизм — это всего лишь две точки зрения на ответ на вопрос о том, на что мы не влияем, принципиальное различие которых является глупостью.
Считать, что существует разница когда именно происходит выбор — эта глупость, как рассуждение о том, как делить шкуру лунного медведя в ситуации когда до луны пешком не добраться. Потому что материя пассивна относительно этого выбора.
Луч разделения вселенных и луч определения выбора, в какую попасть, имеют разную природу, но оба выставляют облучённый объект пассивным участником.
Квантовые вычисления — основано на активном лавировании между этими лучами.
Лучи разделения объектами не детектируются — объекты в параллелях полностью одинаковые. Поэтому лучи могут лететь даже в прошлое. И значит, их вообще можно не учитывать. Ловятся только лучи выбора. А они перемещаются не быстрее света.
Два «луча выбора» могут быть связаны и исключать некоторые комбинации между собой — вот и всё открытие.
и как у любой стоячей волны, у неё будут появляться, так называемые, узлы
Аналогия понятна, но на картинке узлы являются точками, а прогалы между сферами отличны от точек по размеру, и увеличиваются по ширине в отдалении от протона. Или лучше ориентироваться на картинку с трехмерной волной, где прогалы это области где волна в фазе минимума?



Квантовая теория. Вселенная из волн вероятностей