
В детстве я редко ходил в залы аркадных автоматов, потому что особо в них не нуждался, ведь дома у меня были потрясающие игры для C64… но есть три аркадные игры, на которые у меня всегда находились деньги — Donkey Kong, Dragons Lair и Outrun…
… и я очень любил Outrun — скорость, холмы, пальмы и музыка, даже на слабой версии для C64.

Поэтому я решил попробовать написать олдскульную псевдотрёхмерную гоночную игру в стиле Outrun, Pitstop или Pole position. Я не планирую собрать полную и завершённую игру, но мне кажется, будет интересно заново изучить механики, при помощи которых эти игры реализовывали свои трюки. Кривые, холмы, спрайты и ощущение скорости…
Итак, вот мой «проект на выходные», который в итоге занял пять или шесть недель по выходным
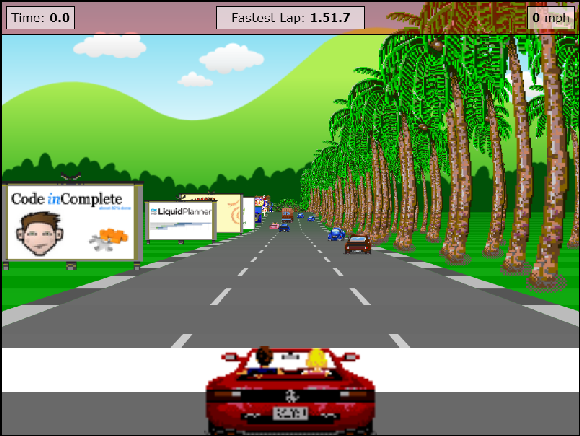
- Сыграть в игру
- Посмотреть исходный код
Играбельная версия больше напоминает техническое демо, чем реальную игру. На самом деле, если вы хотите создать настоящую псевдотрёхмерную гонку, то это будет самый минимальная основа, которую нужно постепенно превратить в игру.
Она не отшлифована, немного уродлива, но полностью функциональна. Я покажу, как реализовать её самостоятельно за четыре простых шага.
Можно также поиграть
О производительности
Производительность этой игры очень сильно зависит от машины/браузера. В современных браузерах она работает хорошо, особенно в тех, где есть GPU-ускорение canvas, но плохой графический драйвер может привести к зависанию. В игре можно менять разрешение рендеринга и расстоянием отрисовки.
О структуре кода
Так получилось, что проект реализован на Javascript (из-за простоты прототипирования), но он не предназначен для демонстрации техник или рекомендованных приёмов Javascript. На самом деле, для простоты понимания Javascript каждого примера встроен непосредственно в HTML-страницу (ужас!); хуже того, в нём используются глобальные переменные и функции.
Если бы я создавал реальную игру, то код был бы гораздо более структурирован и упорядочен, но так как это техническое демо гоночной игры, я решил придерживаться KISS.
Часть 1. Прямые дороги.
Итак, как же нам приступить к созданию псевдотрёхмерной гоночной игры?
Ну, нам потребуется
- Повторить тригонометрию
- Вспомнить основы 3d-проецирования
- Создать игровой цикл
- Загрузить спрайтовые изображения
- Построить геометрию дороги
- Отрендерить фон
- Отрендерить дорогу
- Отрендерить машину
- Реализовать поддержку клавиатуры для управления машиной
Но прежде чем мы начнём, давайте прочитаем Lou’s Pseudo 3d Page [перевод на Хабре] — единственный источник информации (который мне удалось найти) о том, как создать псевдотрёхмерную гоночную игру.
Закончили читать статью Лу? Отлично! Мы будем создавать вариацию его техники «Realistic Hills Using 3d-Projected Segments». Мы будем делать это постепенно, на протяжении следующих четырёх частей. Но начнём мы сейчас, с версии v1, и создадим очень простую геометрию прямой дороги, спроецировав её на HTML5-элемент canvas.
Демо можно посмотреть здесь.
Немного тригонометрии
Прежде чем заняться реализацией, давайте воспользуемся основами тригонометрии, чтобы вспомнить, как спроецировать точку в 3D-мире на 2D-экран.
В самом простейшем случае, если не касаться векторов и матриц, для 3D-проецирования используется закон подобных треугольников.
Используем следующие обозначения:
- h = высота камеры
- d = расстояние от камеры до экрана
- z = расстояние от камеры до машины
- y = координата Y экрана
Тогда мы можем использовать закон подобных треугольников для вычисления
y = h*d/z
как показано на схеме:
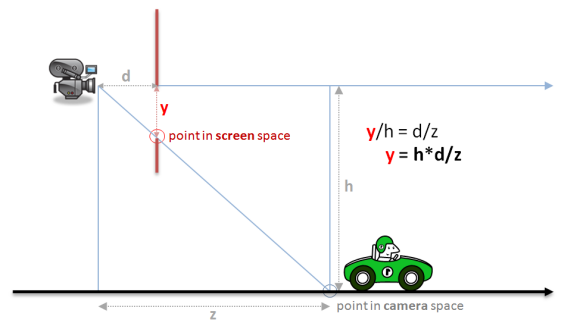
Можно было также нарисовать похожую схему в виде сверху вместо вида сбоку, и вывести похожее уравнение для вычисления координаты X экрана:
x = w*d/z
Где w = половина ширины дороги (от камеры до края дороги).
Как видите, для x, и y мы выполняем масштабирование на коэффициент
d/z
Системы координат
В виде схемы это выглядит красиво и просто, но начав кодить, вы можете немного запутаться, потому что мы выбрали произвольные наименования, и непонятно, чем мы обозначили координаты 3D-мира, а чем координаты 2D-экрана. Также мы предполагаем, что камера находится в центре начала координат мира, хотя в реальности она будет следовать за машиной.
Если подходить более формально, то нам нужно выполнять:
- преобразование из координат мира в координаты экрана
- проецирование координат камеры на нормализованную плоскость проекции
- масштабирование спроецированных координат на координаты физического экрана (в нашем случае это canvas)

Примечание: в настоящей 3d-системе между этапами 1 и 2 выполняется этап поворота, но поскольку мы будем имитировать кривые, то поворот нам не нужен.
Проецирование
Формальные уравнения проецирования можно представить следующим образом:

- Уравнения преобразования (translate) вычисляют точку относительно камеры
- Уравнения проецирования (project) являются вариациями показанного выше «закона подобных треугольников»
- Уравнения масштабирования (scale) учитывают разность между:
- математикой, где 0,0 находится в центре, а ось y направлена вверх, и
- компьютерами, где 0,0 находится в левом верхнем углу, а ось y направлена вниз:

Примечание: в полнофункциональной 3d-системе нам нужно было бы более формально задать классVectorиMatrixдля выполнения более надёжной 3d-математики, и если мы бы сделали это, то стоило бы просто использовать WebGL (или его аналог)… но в нашем проекте это не требуется. Я хотел придерживаться олдскульной псевдотрёхмерности для создания игры в стиле Outrun.
Ещё немного тригонометрии

Последним куском головоломки станет способ вычисления d — расстояния от камеры до плоскости проецирования.
Вместо того, чтобы просто прописывать жёстко заданное значение d, более полезно будет вычислять его из нужной вертикальной области обзора. Благодаря этому мы сможем при необходимости «зумить» камеру.
Если предположить, что мы выполняем проецирование на нормализованную плоскость проецирования, координаты которой находятся в интервале от -1 до +1, то d можно вычислить следующим образом:
d = 1/tan(fov/2)
Задавая fov как одну (из множества) переменных, мы сможем настраивать область обзора для тонкой подстройки алгоритма рендеринга.
Структура кода на Javascript
В начале статьи я уже сказал, что код не совсем соответствует рекомендациям по написанию Javascript — это «быстрое и грязное» демо с простыми глобальными переменными и функциями. Однако поскольку я собираюсь создать четыре отдельные версии (прямые, кривые, холмы и спрайты), то буду хранить некоторые многократно используемые методы внутри
common.js в рамках следующих модулей:- Dom — несколько мелких вспомогательных функций DOM.
- Util — общие утилиты, в основном вспомогательные математические функции.
- Game — общие игровые вспомогательные функции, например, загрузчик изображений и игровой цикл.
- Render — вспомогательные функции рендеринга на canvas.
Подробно я буду объяснять методы из
common.js, только если они относятся к самой игре, а не являются просто вспомогательными математическими или DOM-функциями. Надеюсь, из названия и контекста будет понятно, что должны делать методы.Как обычно, исходный код находится в окончательной документации.
Простой игровой цикл
Прежде чем что-то рендерить, нам нужен игровой цикл. Если вы читали любую из моих предыдущих статей про игры (pong, breakout, tetris, snakes или boulderdash), то уже видели примеры моего любимого игрового цикла с фиксированным шагом времени.
Я не буду вдаваться глубоко в подробности, и просто повторно использую часть кода из предыдущих игр, чтобы создать игровой цикл с фиксированным шагом времени при помощи requestAnimationFrame.
Принцип заключается в том, что каждый из моих четырёх примеров может вызывать
Game.run(...) and и использовать собственные версииupdate— обновление игрового мира с фиксированным шагом времени.render— обновление игрового мира, когда позволяет браузер.
run: function(options) {
Game.loadImages(options.images, function(images) {
var update = options.update, // method to update game logic is provided by caller
render = options.render, // method to render the game is provided by caller
step = options.step, // fixed frame step (1/fps) is specified by caller
now = null,
last = Util.timestamp(),
dt = 0,
gdt = 0;
function frame() {
now = Util.timestamp();
dt = Math.min(1, (now - last) / 1000); // using requestAnimationFrame have to be able to handle large delta's caused when it 'hibernates' in a background or non-visible tab
gdt = gdt + dt;
while (gdt > step) {
gdt = gdt - step;
update(step);
}
render();
last = now;
requestAnimationFrame(frame);
}
frame(); // lets get this party started
});
}Повторюсь, это переделка идей из моих предыдущих игр на canvas, поэтому если вам непонятно, как работает игровой цикл, то вернитесь к одной из предыдущих статей.
Изображения и спрайты
Прежде чем начнётся игровой цикл, мы загружаем два отдельных спрайтшита (листа спрайтов):
- background — три параллаксных слоя для неба, холмов и деревьев
- sprites — спрайты машины (плюс деревья и билборды, которые будут добавлены в окончательную версию)

Спрайтшит был сгенерирован с помощью небольшого таска Rake и Ruby Gem sprite-factory.
Этот таск генерирует объединённые спрайтшиты, а также координаты x,y,w,h, которые будут храниться в константах
BACKGROUND и SPRITES.Примечание: фоны созданы мной при помощи Inkscape, а большинство спрайтов — это графика, позаимствованная из старой версии Outrun для Genesis и использованная в качестве обучающих примеров.
Игровые переменные
В дополнение к изображениям фонов и спрайтов нам понадобится несколько игровых переменных, а именно:
var fps = 60; // how many 'update' frames per second
var step = 1/fps; // how long is each frame (in seconds)
var width = 1024; // logical canvas width
var height = 768; // logical canvas height
var segments = []; // array of road segments
var canvas = Dom.get('canvas'); // our canvas...
var ctx = canvas.getContext('2d'); // ...and its drawing context
var background = null; // our background image (loaded below)
var sprites = null; // our spritesheet (loaded below)
var resolution = null; // scaling factor to provide resolution independence (computed)
var roadWidth = 2000; // actually half the roads width, easier math if the road spans from -roadWidth to +roadWidth
var segmentLength = 200; // length of a single segment
var rumbleLength = 3; // number of segments per red/white rumble strip
var trackLength = null; // z length of entire track (computed)
var lanes = 3; // number of lanes
var fieldOfView = 100; // angle (degrees) for field of view
var cameraHeight = 1000; // z height of camera
var cameraDepth = null; // z distance camera is from screen (computed)
var drawDistance = 300; // number of segments to draw
var playerX = 0; // player x offset from center of road (-1 to 1 to stay independent of roadWidth)
var playerZ = null; // player relative z distance from camera (computed)
var fogDensity = 5; // exponential fog density
var position = 0; // current camera Z position (add playerZ to get player's absolute Z position)
var speed = 0; // current speed
var maxSpeed = segmentLength/step; // top speed (ensure we can't move more than 1 segment in a single frame to make collision detection easier)
var accel = maxSpeed/5; // acceleration rate - tuned until it 'felt' right
var breaking = -maxSpeed; // deceleration rate when braking
var decel = -maxSpeed/5; // 'natural' deceleration rate when neither accelerating, nor braking
var offRoadDecel = -maxSpeed/2; // off road deceleration is somewhere in between
var offRoadLimit = maxSpeed/4; // limit when off road deceleration no longer applies (e.g. you can always go at least this speed even when off road)Некоторые из них можно настраивать при помощи элементов управления UI для изменения критически важных значений в процессе выполнения программы, чтобы можно было увидеть, как они влияют на рендеринг дороги. Другие повторно вычисляются из настраиваемых UI значений в методе
reset().Управляем Ferrari
Мы выполняем привязку клавиш для
Game.run, которая обеспечивает простой ввод с клавиатуры, задающий или сбрасывающий переменные, сообщающие о текущих действиях игрока:Game.run({
...
keys: [
{ keys: [KEY.LEFT, KEY.A], mode: 'down', action: function() { keyLeft = true; } },
{ keys: [KEY.RIGHT, KEY.D], mode: 'down', action: function() { keyRight = true; } },
{ keys: [KEY.UP, KEY.W], mode: 'down', action: function() { keyFaster = true; } },
{ keys: [KEY.DOWN, KEY.S], mode: 'down', action: function() { keySlower = true; } },
{ keys: [KEY.LEFT, KEY.A], mode: 'up', action: function() { keyLeft = false; } },
{ keys: [KEY.RIGHT, KEY.D], mode: 'up', action: function() { keyRight = false; } },
{ keys: [KEY.UP, KEY.W], mode: 'up', action: function() { keyFaster = false; } },
{ keys: [KEY.DOWN, KEY.S], mode: 'up', action: function() { keySlower = false; } }
],
...
}Состоянием игрока управляют следующие переменные:
- speed — текущая скорость.
- position — текущая позиция по Z на трассе. Заметьте, что это позиция камеры, а не Ferrari.
- playerX — текущая позиция игрока по X на дороге. Нормализована в интервале от -1 до +1, чтобы не зависеть от действительного значения
roadWidth.
Эти переменные задаются внутри метода
update, который выполняет следующие действия:- обновляет
positionна основании текущейspeed. - обновляет
playerXпри нажатии на клавиши «влево» или «вправо». - увеличивает
speed, если нажата клавиша «вверх». - уменьшает
speed, если нажата клавиша «вниз». - уменьшает
speed, если не нажаты клавиши «вверх» и «вниз». - уменьшает
speed, еслиplayerXнаходится за краем дороги и на траве.
В случае прямых дорог метод
update довольно ясен и прост:function update(dt) {
position = Util.increase(position, dt * speed, trackLength);
var dx = dt * 2 * (speed/maxSpeed); // at top speed, should be able to cross from left to right (-1 to 1) in 1 second
if (keyLeft)
playerX = playerX - dx;
else if (keyRight)
playerX = playerX + dx;
if (keyFaster)
speed = Util.accelerate(speed, accel, dt);
else if (keySlower)
speed = Util.accelerate(speed, breaking, dt);
else
speed = Util.accelerate(speed, decel, dt);
if (((playerX < -1) || (playerX > 1)) && (speed > offRoadLimit))
speed = Util.accelerate(speed, offRoadDecel, dt);
playerX = Util.limit(playerX, -2, 2); // dont ever let player go too far out of bounds
speed = Util.limit(speed, 0, maxSpeed); // or exceed maxSpeed
}Не волнуйтесь, он станет намного сложнее, когда в готовой версии мы добавим спрайты и распознавание коллизий.
Геометрия дороги
Прежде чем мы сможем рендерить игровой мир, нам нужно построить массив из
segments в методе resetRoad().Каждый из этих сегментов дороги в конце концов будет спроецирован из его мировых координат, чтобы он превратился в 2d-полигон в экранных координатах. Для каждого сегмента мы храним две точки, p1 — это центр наиболее близкого к камере ребра, а p2 — центр самого дальнего от камеры ребра.

Строго говоря, p2 каждого сегмента идентична p1 предыдущего сегмента, но мне кажется, что проще хранить их как отдельные точки, и преобразовывать каждый сегмент по отдельности.
Мы храним отдельную
rumbleLength потому, что у нас могут быть красивые детализированные кривые и холмы, но в то же время и горизонтальные полосы. Если каждый следующий сегмент будет иметь другой цвет, то это создаст нехороший эффект стробоскопа. Поэтому мы хотим иметь множество мелких сегментов, но сгруппировать их вместе, чтобы образовать отдельные горизонтальные полосы.function resetRoad() {
segments = [];
for(var n = 0 ; n < 500 ; n++) { // arbitrary road length
segments.push({
index: n,
p1: { world: { z: n *segmentLength }, camera: {}, screen: {} },
p2: { world: { z: (n+1)*segmentLength }, camera: {}, screen: {} },
color: Math.floor(n/rumbleLength)%2 ? COLORS.DARK : COLORS.LIGHT
});
}
trackLength = segments.length * segmentLength;
}Мы инициализируем p1 и p2 только со значениями мировых координат z, потому что нам нужны только прямые дороги. Координаты y всегда будут равны 0, а координаты x всегда будут зависеть от масштабированного значения
+/- roadWidth. Позже, когда мы добавим кривые и холмы, эта часть изменится.Также мы зададим пустые объекты для хранения представлений этих точек в камере и на экране, чтобы не создавать кучу временных объектов в каждом
render. Чтобы до минимума снизить объём сборки мусора, мы должны избегать выделения объектов внутри игрового цикла.Когда машина достигает конца дороги, мы просто возвращаемся в начало цикла. Чтобы упростить это, мы создадим метод для нахождения сегмента для любого значения Z, даже если он выходит за пределы длины дороги:
function findSegment(z) {
return segments[Math.floor(z/segmentLength) % segments.length];
}Рендеринг фона
Метод
render() начинается с отрисовки фонового изображения. В следующих частях, где мы добавим кривые и холмы, нам нужно будет, чтобы фон выполнял параллаксный скроллинг, поэтому мы уже сейчас начнём двигаться в этом направлении, выполняя рендеринг фона как трёх отдельных слоёв:function render() {
ctx.clearRect(0, 0, width, height);
Render.background(ctx, background, width, height, BACKGROUND.SKY);
Render.background(ctx, background, width, height, BACKGROUND.HILLS);
Render.background(ctx, background, width, height, BACKGROUND.TREES);
...Рендеринг дороги
Затем функция render итеративно проходит по всем сегментам и проецирует p1 и p2 каждого сегмента из мировых координат в экранные, при необходимости обрезая сегмент, а в противном случае выполняя его рендеринг:
var baseSegment = findSegment(position);
var maxy = height;
var n, segment;
for(n = 0 ; n < drawDistance ; n++) {
segment = segments[(baseSegment.index + n) % segments.length];
Util.project(segment.p1, (playerX * roadWidth), cameraHeight, position, cameraDepth, width, height, roadWidth);
Util.project(segment.p2, (playerX * roadWidth), cameraHeight, position, cameraDepth, width, height, roadWidth);
if ((segment.p1.camera.z <= cameraDepth) || // behind us
(segment.p2.screen.y >= maxy)) // clip by (already rendered) segment
continue;
Render.segment(ctx, width, lanes,
segment.p1.screen.x,
segment.p1.screen.y,
segment.p1.screen.w,
segment.p2.screen.x,
segment.p2.screen.y,
segment.p2.screen.w,
segment.color);
maxy = segment.p2.screen.y;
}Выше мы уже видели вычисления, необходимые для проецирования точки; версия на javascript объединяет преобразование, проецирование и масштабирование в один метод:
project: function(p, cameraX, cameraY, cameraZ, cameraDepth, width, height, roadWidth) {
p.camera.x = (p.world.x || 0) - cameraX;
p.camera.y = (p.world.y || 0) - cameraY;
p.camera.z = (p.world.z || 0) - cameraZ;
p.screen.scale = cameraDepth/p.camera.z;
p.screen.x = Math.round((width/2) + (p.screen.scale * p.camera.x * width/2));
p.screen.y = Math.round((height/2) - (p.screen.scale * p.camera.y * height/2));
p.screen.w = Math.round( (p.screen.scale * roadWidth * width/2));
}Кроме вычисления экранных x и y для каждых точек p1 и p2 мы используем те же вычисления проецирования для вычисления спроецированной ширины (w) сегмента.
Имея экранные координаты x и y точек p1 и p2, а также спроецированную ширину дороги w, мы можем довольно просто вычислить при помощи вспомогательной функции
Render.segment все полигоны, необходимые ей для рендеринга травы, дороги, горизонтальных полос и разделительных линий, воспользовавшись общей вспомогательной функцией Render.polygon (см. common.js).Рендеринг машины
Наконец, последнее, что требуется методу
render — это рендеринг Ferrari: Render.player(ctx, width, height, resolution, roadWidth, sprites, speed/maxSpeed,
cameraDepth/playerZ,
width/2,
height);Этот метод называется
player, а не car, потому что в окончательной версии игры на дороге будут и другие машины, и мы хотим отделить Ferrari игрока от других машин.Вспомогательная функция
Render.player использует метод canvas под названием drawImage для рендеринга спрайта, предварительно отмасштабировав его при помощи того же масштабирования проекции, которое использовалось раньше:d/z
Где z в данном случае — это относительное расстояние от машины до камеры, хранящееся в переменной playerZ.
Кроме того, функция немного «трясёт» машину на высоких скоростях, добавляя в уравнение масштабирования немного случайности, зависящей от speed/maxSpeed.
И вот что у нас получилось:

Заключение
Мы проделали довольно большой объём работы только для того, чтобы создать систему с прямыми дорогами. Мы добавили
- общий вспомогательный модуль Dom
- общий математический вспомогательный модуль Util
- общий вспомогательный canvas-модуль Render...
- … в том числе
Render.segment,Render.polygonиRender.sprite - игровой цикл с фиксированным шагом
- загрузчик изображений
- обработчик клавиатуры
- фон с параллаксными слоями
- спрайтшит с автомобилями, деревьями и билбордами
- рудиментарную геометрию дороги
- метод
update()для управления машиной - метод
render()для рендеринга фона, дороги и машины игрока - HTML5-тег
<audio>с гоночной музыкой (скрытый бонус!)
… что дало нам хороший фундамент для дальнейшего развития.
Часть 2. Кривые.

В этой части мы подробнее расскажем, как работают кривые.
В предыдущей части мы составили геометрию дороги в виде массива сегментов, каждый из которых имеет мировые координаты, преобразуемые относительно камеры, а затем проецируются на экран.
Нам нужна была только мировая координата z для каждой точки, потому что на прямых дорогах и x, и y были равны нулю.

Если бы мы создавали полнофункциональную 3d-систему, то могли бы реализовать кривые, вычисляя x и z полосы многоугольников, показанных выше. Однако такой тип геометрии будет довольно непросто вычислять, и для этого потребуется добавить в уравнения проецирования этап 3d-поворота…
… если бы мы двинулись этим путём, то лучше было бы использовать WebGL или его аналоги, но этот проект не у нашего проекта другие задачи. Мы просто хотим использовать для имитации кривых олдскульные псевдотрёхмерные трюки.
Поэтому вы наверно удивитесь, узнав, что мы вообще не будем вычислять координаты x сегментов дороги…
Вместо этого мы воспользуемся советом Лу:
«чтобы искривить дорогу, достаточно просто изменить позицию центральной линии формы кривой… начиная с низа экрана, величина сдвига центра дороги влево или вправо постепенно увеличивается».
В нашем случае центральной линией является значение
cameraX, передаваемое в вычисления проецирования. Это означает, что когда мы выполняем render() каждого сегмента дороги, можно имитировать кривые, сдвигая значение cameraX на постепенно возрастающую величину.
Чтобы знать, на сколько выполнять сдвиг, нам нужно хранить в каждом сегменте значение
curve. Эта величина обозначает, на сколько сегмент должен быть сдвинут от центральной линии камеры. Она будет:- отрицательной для поворачивающих налево кривых
- положительной для поворачивающих вправо кривых
- меньше для плавных кривых
- больше для резких кривых
Сами значения выбираются довольно произвольно; путём проб и ошибок мы можем подобрать хорошие значения, при которых кривые кажутся «правильными»:
var ROAD = {
LENGTH: { NONE: 0, SHORT: 25, MEDIUM: 50, LONG: 100 }, // num segments
CURVE: { NONE: 0, EASY: 2, MEDIUM: 4, HARD: 6 }
};Кроме подбора хороших значений для кривых нам нужно избегать любых разрывов в переходах, когда прямая превращается в кривую (или наоборот). Это можно реализовать смягчением при входе и выходе из кривых. Мы сделаем это, постепенно увеличивая (или уменьшая) значение
curve для каждого сегмента при помощи традиционных функций плавности, пока оно не достигнет нужного значения:easeIn: function(a,b,percent) { return a + (b-a)*Math.pow(percent,2); },
easeOut: function(a,b,percent) { return a + (b-a)*(1-Math.pow(1-percent,2)); },
easeInOut: function(a,b,percent) { return a + (b-a)*((-Math.cos(percent*Math.PI)/2) + 0.5); },То есть теперь, с учётом функции добавления одного сегмента к геометрии…
function addSegment(curve) {
var n = segments.length;
segments.push({
index: n,
p1: { world: { z: n *segmentLength }, camera: {}, screen: {} },
p2: { world: { z: (n+1)*segmentLength }, camera: {}, screen: {} },
curve: curve,
color: Math.floor(n/rumbleLength)%2 ? COLORS.DARK : COLORS.LIGHT
});
}мы можем создать метод для плавного входа, нахождения и плавного выхода с искривлённой дороги:
function addRoad(enter, hold, leave, curve) {
var n;
for(n = 0 ; n < enter ; n++)
addSegment(Util.easeIn(0, curve, n/enter));
for(n = 0 ; n < hold ; n++)
addSegment(curve);
for(n = 0 ; n < leave ; n++)
addSegment(Util.easeInOut(curve, 0, n/leave));
}… а поверх можно наложить дополнительную геометрию, например, S-образные кривые:
function addSCurves() {
addRoad(ROAD.LENGTH.MEDIUM, ROAD.LENGTH.MEDIUM, ROAD.LENGTH.MEDIUM, -ROAD.CURVE.EASY);
addRoad(ROAD.LENGTH.MEDIUM, ROAD.LENGTH.MEDIUM, ROAD.LENGTH.MEDIUM, ROAD.CURVE.MEDIUM);
addRoad(ROAD.LENGTH.MEDIUM, ROAD.LENGTH.MEDIUM, ROAD.LENGTH.MEDIUM, ROAD.CURVE.EASY);
addRoad(ROAD.LENGTH.MEDIUM, ROAD.LENGTH.MEDIUM, ROAD.LENGTH.MEDIUM, -ROAD.CURVE.EASY);
addRoad(ROAD.LENGTH.MEDIUM, ROAD.LENGTH.MEDIUM, ROAD.LENGTH.MEDIUM, -ROAD.CURVE.MEDIUM);
}Изменения в методе update()
Единственные изменения, которые необходимо внести в метод
update() — это приложение своего рода центробежной силы, когда машина движется по кривой.Мы задаём произвольный множитель, который можно настраивать в соответствии с нашими предпочтениями.
var centrifugal = 0.3; // centrifugal force multiplier when going around curvesА затем мы просто будем обновлять позицию
playerX на основании его текущей скорости, величины curve и множителя центробежной силы:playerX = playerX - (dx * speedPercent * playerSegment.curve * centrifugal);Рендеринг кривых
Выше мы говорили, что можно рендерить имитируемые кривые, смещая значение
cameraX, используемое в вычислениях проецирования, в процессе выполнения render() каждого сегмента дороги.
Для этого мы будем хранить переменную накопителя dx, увеличивающуюся для каждого сегмента на значение
curve, а также переменную x, которая будет использоваться как смещение значения cameraX, используемого в вычислениях проецирования.Для реализации кривых нам нужно следующее:
- смещаем проекцию p1 каждого сегмента на x
- смещаем проекцию p2 каждого сегмента на x + dx
- увеличиваем x для следующего сегмента на dx
Наконец, чтобы избежать рваных переходов при пересечении границ сегментов, мы должны сделать так, чтобы dx инициализировалась интерполированным значением кривой текущих базовых сегментов.
Изменим метод
render() следующим образом:var baseSegment = findSegment(position);
var basePercent = Util.percentRemaining(position, segmentLength);
var dx = - (baseSegment.curve * basePercent);
var x = 0;
for(n = 0 ; n < drawDistance ; n++) {
...
Util.project(segment.p1, (playerX * roadWidth) - x, cameraHeight, position - (segment.looped ? trackLength : 0), cameraDepth, width, height, roadWidth);
Util.project(segment.p2, (playerX * roadWidth) - x - dx, cameraHeight, position - (segment.looped ? trackLength : 0), cameraDepth, width, height, roadWidth);
x = x + dx;
dx = dx + segment.curve;
...
}Фон с параллаксным скроллингом
Наконец, нам нужно выполнять скроллинг параллаксных слоёв фона, храня смещение для каждого слоя…
var skySpeed = 0.001; // background sky layer scroll speed when going around curve (or up hill)
var hillSpeed = 0.002; // background hill layer scroll speed when going around curve (or up hill)
var treeSpeed = 0.003; // background tree layer scroll speed when going around curve (or up hill)
var skyOffset = 0; // current sky scroll offset
var hillOffset = 0; // current hill scroll offset
var treeOffset = 0; // current tree scroll offset… и увеличивая его во время
update() в зависимости от величины curve текущего сегмента игрока и его скорости…skyOffset = Util.increase(skyOffset, skySpeed * playerSegment.curve * speedPercent, 1);
hillOffset = Util.increase(hillOffset, hillSpeed * playerSegment.curve * speedPercent, 1);
treeOffset = Util.increase(treeOffset, treeSpeed * playerSegment.curve * speedPercent, 1);… а затем использовать использовать это смещение при выполнении
render() слоёв фона.Render.background(ctx, background, width, height, BACKGROUND.SKY, skyOffset);
Render.background(ctx, background, width, height, BACKGROUND.HILLS, hillOffset);
Render.background(ctx, background, width, height, BACKGROUND.TREES, treeOffset);Заключение
Итак, вот мы и получили фальшивые псевдотрёхмерные кривые:

Основная часть добавленного нами кода заключается в построении геометрии дороги с соответствующим значением
curve. Реализовав её, добавить центробежную силу во время update() намного проще.Рендеринг кривых выполняется всего в нескольких строках кода, но может быть сложно понять (и описать), что же конкретно здесь происходит. Существует множество способов имитации кривых и очень легко забрести при их реализации в тупик. Ещё проще увлечься посторонней задачей и попробовать сделать всё «правильно»; прежде чем успеете осознать это, вы начнёте создавать полнофункциональную 3d-систему с матрицами, поворотами и настоящей 3d-геометрией… которые, как я сказал, не являются нашей задачей.
При написании этой статьи я был уверен, что в моей реализации кривых определённо есть проблемы. Пытаясь визуализировать алгоритм, я не понимал, зачем мне понадобились два значения накопителей dx и x вместо одного… а если я не могу чего-то полностью объяснить, то где-то что-то пошло не так…
… но время работы над проектом «на выходные» почти истекло, и, честно говоря, кривые кажутся мне вполне красивыми, и в конечном итоге, это самое важное.



