Комментарии 42
Все хорошо, только вместе с картинками интересней было бы видеть пошаговые примеры кода, который это делает.
Раз вы так хорошо разбираетесь в небесной механике, не могли бы вы добавить в простейшую модель вращения 2х тел одинаковой массы вокруг общего центра ненулевую скорость распространения гравитационного возмущения. Т.е. когда одна из масс m1 уже пролетела по своей круговой траектории некоторое расстояние, другая масса m2 все еще «ощущает», что m1 находится где-то на своей траектории в предыдущем положении. Ведь так работает запаздывание возмущения? Если так, то должна появляться сила ускоряющая вращение этих 2х масс. И притягивающиеся массы должны со временем оттолкнуться друг от друга. Ну чем, не темная энергия, с отрицательной массой и действием на огромных расстояниях.
ненулевую скорость распространения гравитационного возмущения
А ее тут вроде за нулевую и не принимают, а за мгновенную а не 300000 км/с, и для простой модели это нормально.
другая масса m2 все еще «ощущает», что m1 находится где-то на своей траектории в предыдущем положении
Долго «ощущает»… очень долго…
И притягивающиеся массы должны со временем оттолкнуться друг от друга.
И из чего сие следует?
Если я ещё правильно понимаю русский язык, скорость не может быть «мгновенной».
«Долго ощущает»
Ощущает действительно долго — бесконечно долго. Пока частица существует, она ощущает притяжение других тел.
Я так понимаю, вы неудачно попытались съязвить о малом времени распространения сигнала от одной частицы к другой.
Ну и что? Вы пытаетесь аргументировать отсутствие эффекта его слабым проявлением?
Кстати, бывает и «долго»: 100тыс св.лет — диаметр млечного пути.
Поднятый выше вопрос о том, как релятивистские эффекты меняют классическую небесную механику не является тривиальным, и если у вас есть что сказать по теме — милости просим.
Если я ещё правильно понимаю русский язык, скорость не может быть «мгновенной».Мгновенная скорость (in English — instantaneous velocity) — скорость в данный момент времени в данной точке траектории. В любой точке криволинейной траектории она направлена по касательной к траектории в этой точке.
Обычно под скоростью понимают именно мгновенную скорость, т. е. скорость в определенный момент времени. См. школьные учебники физики.
Для знатоков русского языка, ещё бывает средняя скорость (average velocity).
Автор тут рассматривает не небесную механику как таковую, а скорее некоторые упрошенные примеры для иллюстрации
>> Интересно получается, везде нас преследует математика.
Кто бы мог подумать!
Кто бы мог подумать!
Если кольца Сатурна это раздробленные спутники, бывшие очень крупными, то это отличный способ покопать бывшее ядро планеты. Туда должны были упасть тяжелые элементы, прекрасное месторождение тяжелого металла обогащенного гравитацией.
Хватит горы, высотой 100 километров и недюжинной силы. Но насколько сильно нужно пнуть мяч, чтобы он никогда больше не вернулся на Землю? Как отправить мяч в путешествие к звёздам, имея только грубую силу и знание небесной механики?
Тема сабжа осталась не раскрытой, с какой силой нужно пнуть мяч (ну или сколько нужно приложить энергии к мячу весом 1 кг, отправив в полет под углом 45° к горизонту), чтобы тот вышел на орбиту Земли?
p.s. я не настоящий сварщик, а точнее совсем не сварщик, пришел только к подсчету потенциальной энергии мяча на минимально возможной орбите вокруг Земли (гугл выдал высоту в 160 км, это конечно же, пренебрегая сопротивлением воздуха), поэтому свои выкладки выложить не рискну, но вопрос заинтересовал :)
Правильный ответ, пренебрегая атмосферой — мяч одним импульсом вывести на орбиту невозможно. Он либо прилетит обратно на землю, либо покинет орбиту. Для того, чтобы мяч остался на орбите, в апогее ему надо придать еще один импульс, который поднимет перигей выше поверхности земли. А так — любая замкнутая орбита приведет вас в ту же точку через виток с тем же вектором скорости, то есть, ваш мяч должен был бы в какой-то момент выпрыгнуть из горы под углом 45°, если убрать гору, Землю, и все остальное, что ему помешает это сделать.
Вы абсолютно правы, пытался оценить порядок величины энергии, необходимой для того, чтобы мяч покинул орбиту, и совершенно не учел того, что не получится так просто зафиксировать мяч на орбите.
пренебрегая атмосферой
Под 45 градусов действительно не получится, а паралельно поверхности Земли — почему бы и нет.
Подозреваю, автор считал минимальной орбитой те самые 100км.
Пнуть мяч на 8км/с и не порвать — уметь надо.
Мяч одним импульсом вывести на орбиту не получится. Я смоделировал предлагаемую вами ситуацию:
Мяч или падает обратно (если скорость меньше второй космической), или улетает безвозвратно (если больше). Но мяч можно вывести на орбиту, дав ему еще один импульс в точке, обведённой красным.
Мяч или падает обратно (если скорость меньше второй космической), или улетает безвозвратно (если больше). Но мяч можно вывести на орбиту, дав ему еще один импульс в точке, обведённой красным.
Прошу прощения, но:
Минимальная скорость, необходимая для выхода на орбиту Земли называется первой комической скоростью.Уж больно бросилось в глаза.
Похоже, вы пишете с десктопа, а тут есть Ctrl+Enter для опечаток.
Спасибо! Забавная ошибка. Исправил.
Если строго судить, там ошибка не в буквах, а в смысле. Первая космическая — это не скорость выведения, а скорость удержания на орбите. То есть чтобы вывести (даже если мгновенно) нужно увеличить потенциальную энергию тела (поднять), после чего придать телу скорость удержания на этой высоте.
Подобную ошибку часто встречаю — если по этой логике (первая космическая убывает с высотой), чем выше поднимать тело, тем это меньше требует затрат. А в реальности, имеем линейный рост потенциальной энергии и и нелинейный по кинетической — чем выше, чем меньшую скорость надо придать телу, но прирост потенциальной энергии больше выигрыша в кинетической.
Это очень легко проследить, если не брать готовую формулу для скорости, а вывести ее самому из закона сохранения полной мех. энергии (дважды — какую скорость придать телу в «перегее» на поверхности, чтоб в апогее достичь нужной высоты и насколько увеличить скорость в апогее, чтоб ускорить ее до круговой этой высоты)
Подобную ошибку часто встречаю — если по этой логике (первая космическая убывает с высотой), чем выше поднимать тело, тем это меньше требует затрат. А в реальности, имеем линейный рост потенциальной энергии и и нелинейный по кинетической — чем выше, чем меньшую скорость надо придать телу, но прирост потенциальной энергии больше выигрыша в кинетической.
Это очень легко проследить, если не брать готовую формулу для скорости, а вывести ее самому из закона сохранения полной мех. энергии (дважды — какую скорость придать телу в «перегее» на поверхности, чтоб в апогее достичь нужной высоты и насколько увеличить скорость в апогее, чтоб ускорить ее до круговой этой высоты)
Вторая попытка.
Раз вы так хорошо разбираетесь в небесной механике, не могли бы вы добавить в простейшую модель вращения 2х тел одинаковой массы вокруг общего центра немгновенную скорость распространения гравитационного возмущения.
Т.е. когда одна из масс m1 уже пролетела по своей круговой траектории из точки P1 в точку P2 (выберем время, которое как раз необходимо для распространения гравитационного возмущения от m1 до m2), другая масса m2 тоже переместившаяся немного вперед взаимодействует с гравитационным возмущение от m1, которая находилась ранее в точке траектории P1. Но сейчас сама m1 в точке P2. Ведь так работает запаздывание возмущения? Если так, то должна появляться сила ускоряющая вращение m2, за счет того, что вектор притяжения будет направлен не точно перпендиклярно вектору скорости m2, а на точку P1, т.е. немного вперед. Со временем система должна ускоряться и потом разлететься, при взаимодействии с другими случайно встретившимися массами. Ну чем, не темная материя, с отрицательной массой, с действием на огромных расстояниях и с взамодействием с отсутствующими объектами (m2 взаимодействует с m1 которая уже не находится в точке P1).
Раз вы так хорошо разбираетесь в небесной механике, не могли бы вы добавить в простейшую модель вращения 2х тел одинаковой массы вокруг общего центра немгновенную скорость распространения гравитационного возмущения.
Т.е. когда одна из масс m1 уже пролетела по своей круговой траектории из точки P1 в точку P2 (выберем время, которое как раз необходимо для распространения гравитационного возмущения от m1 до m2), другая масса m2 тоже переместившаяся немного вперед взаимодействует с гравитационным возмущение от m1, которая находилась ранее в точке траектории P1. Но сейчас сама m1 в точке P2. Ведь так работает запаздывание возмущения? Если так, то должна появляться сила ускоряющая вращение m2, за счет того, что вектор притяжения будет направлен не точно перпендиклярно вектору скорости m2, а на точку P1, т.е. немного вперед. Со временем система должна ускоряться и потом разлететься, при взаимодействии с другими случайно встретившимися массами. Ну чем, не темная материя, с отрицательной массой, с действием на огромных расстояниях и с взамодействием с отсутствующими объектами (m2 взаимодействует с m1 которая уже не находится в точке P1).
Взаимодействие на огромных расстояниях и релятивистские эффекты — это те вещи, которые заслуживают отдельного рассмотрения. Интересно было бы расширить симуляцию и добавить «Эйнштейновские» законы, это бы очень сильно изменило наблюдаемые явления. Что касается системы из двух тел: для получения хотя бы малейшей силы отталкивания скорость их движения должна быть огромной, что подвергнет систему большому количеству других сил, например, испускание гравитационных волн, которое наоборот «забирает» энергию у системы. Во всяком случае это очень интересно было бы наблюдать.
Спасибо за комментарий!
Спасибо за комментарий!
Когда в наших школах на уроках физики или астрономии детям показывают презентацию с GIF-кой из четырёх кадров, где Земля скачет вокруг Солнца — это называет внедрение современных технологий в образовательный процесс. Ведь могли бы и по истлевшим от времени таблицам учиться, сорванцы. Уверена, если бы хоть что-то ученики разбирали на подобных моделях, да ещё и с таким доступным объяснением — заинтересованных в учёбе и науке ребят было бы в разы больше
Помню, еще в школе, на бейсике или паскале писал подобную симуляцию. Но сделал дурацкую ошибку — разложил вектор притяжения по осям х и у и считал каждую компоненту раздельно. В некоторые моменты естественно эти компоненты оказывались нулевые, а сила притяжения бесконечной. Долго не мог понять, почему меня планеты выписывали странные кренделя, а иногда программа вылетала с «division by zero»
Поделитесь, как вообще можно в вычислениях на компьютере вектор не разбивать на компоненты? В коде автора данного поста, конечно, тоже вектора представляются парами чисел — проекциями на оси x и y.
я не помню подробностей, но что-то вроде того:
вектор R разделял на компоненты по X и Y
и считал F по формулам тоже раздельно Fx = G * m1 * m2 / x^2 и Fy = G * m1 * m2 / y^2
Расстояние R может быть большим, но если планеты оказываются на одной оси, т.е. их координаты Y или X очень близки, то и соответствующая компонента F стремилась к бесконечности.
вектор R разделял на компоненты по X и Y
и считал F по формулам тоже раздельно Fx = G * m1 * m2 / x^2 и Fy = G * m1 * m2 / y^2
Расстояние R может быть большим, но если планеты оказываются на одной оси, т.е. их координаты Y или X очень близки, то и соответствующая компонента F стремилась к бесконечности.
Вращение планет вокруг Солнца и добавление в систему малого тела — одни из первых моих шагов в программировании, 20+ лет назад )))
То был чистый Паскаль, а из библиотек — только графика; пожалуй, первая в моей жизни графика.
То был чистый Паскаль, а из библиотек — только графика; пожалуй, первая в моей жизни графика.
Уточните, пожалуйста, какую численную схему вы использовали? Она сохраняет импульс и энергию?
C небольшой модификацией кода можно поиграться приближенным молекулярным взаимодейстием черз потенциал Леннарда Джонса или похожий
OPENCl у меня давал ~50 кратное ускорение относитльно CPU
если притяжение брать 1/RR
а отталкивание 1/R^12 то получится гравитация с автоматичеким слипанием
только в блитжнейц зоне нужно сильно дробить шаг
OPENCl у меня давал ~50 кратное ускорение относитльно CPU
если притяжение брать 1/RR
а отталкивание 1/R^12 то получится гравитация с автоматичеким слипанием
только в блитжнейц зоне нужно сильно дробить шаг
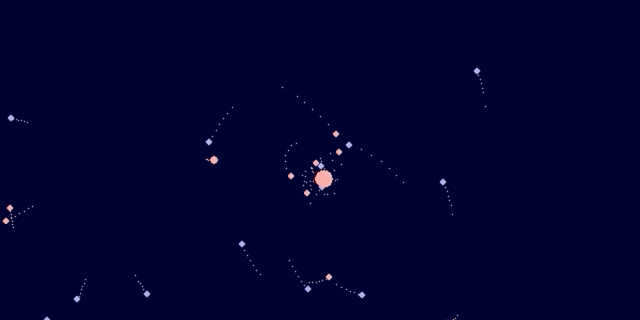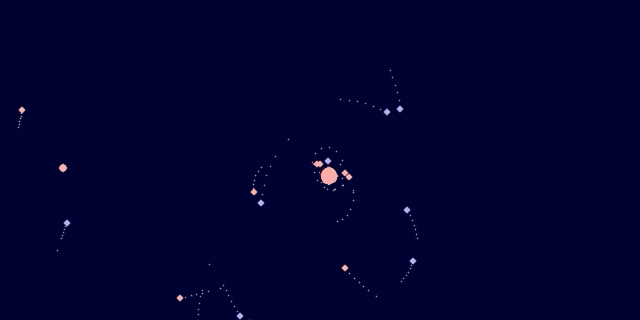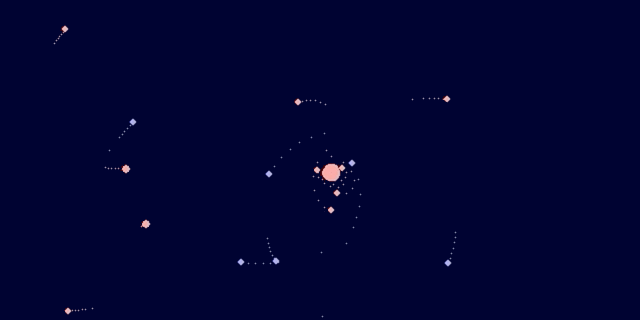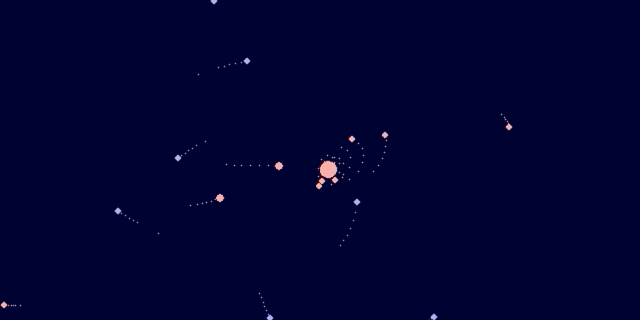
Уже сто лет хотел сделать такую штуку и всё ноги не доходили.
А теперь предложения:
- 01egarh, не хотите выложить код на github.com?
- И интерфейсик бы к этому всему, чтобы можно было рулить параметрами Вселенной в реальном времени :) Еще в молодости баловался с Interactive Physics (с бесплатной версией, которая работала полчаса и не давала сохранять) — там можно было задавать кучу физических параметров для объектов, накидать контролов на поле и рулить физикой в процессе.
- Классно было бы еще как-то показывать вращение точки и продумать сохранение момента импульса, чтобы в сумме с контролами (см. предыдущий пункт) можно было изображать нейтронную звезду.
01egarh, я чего-то не понимаю.
А именно, как с помощью первой формулы вычислить vx/vy для планеты, вращающейся вокруг Солнца. Пока что имею что-то подобное на:
def planet(sun, orb, color, r = 6, m = 15):
vx = -(orb * G / (orb * 1.25)) ** 0.5
return Ball(sun.x, sun.y - orb, color, r = r, mass = m, vx = vx), где orb — высота орбиты (круговой) над Солнцем.
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Моделируем вселенную: небесная механика наглядно