ErmIg 11 дек 2019 в 15:29

Сверточный слой: быстрая свертка по методу Шмуэля Винограда

8 мин

9.8K

C++*Алгоритмы*Обработка изображений*Машинное обучение*

Введение

Данная статья является продолжением серии статей описывающей алгоритмы лежащие в основе
Synet — фреймворка для запуска предварительно обученных нейронных сетей на CPU.

В предыдущей статье я описал методы, основанные на матричном умножении. Эти методы с минимальными усилиями позволяют достичь во многих случаях более 80% от теоретического максимума. Казалось бы, ну куда тут можно еще дальше улучшать? Оказывается можно! Существуют математически методы, которые позволяют сократить число операций, необходимых для свертки. С одним из таких методов — алгоритму свертки по методу Винограда мы и ознакомимся в настоящей статье.

Шмуэль Виноград (Shmuel Winograd) 1936.01.04 — 2019.03.25 — выдающийся израильский и американский ученый в области компьютерных наук, создатель алгоритмов быстрого матричного умножения, свертки и преобразования Фурье.

Немного математики

Хотя, в машинном обучении наиболее часто используют свертки с квадратным ядром, мы с целью упрощения изложения, вначале рассмотрим одномерный случай. Пусть у нас есть входное одномерное изображение размером $1\times4$ :

$d= \begin{bmatrix}d_0 & d_1 & d_2 & d_3\end{bmatrix}^T,$

и фильтр размером $1\times3$ :

$g= \begin{bmatrix}g_0 & g_1 & g_2\end{bmatrix}^T,$

тогда результатом свертки будет:

$F(2,3)= \begin{bmatrix}d_0 g_0+d_1 g_1+d_2 g_2 \\ d_1 g_0+d_2 g_1+d_3 g_2\end{bmatrix}.$

Эти выражения будет удобно переписать в матричной форме:

$F(2,3)=\begin{bmatrix}d_0 & d_1 & d_2 \\ d_1 & d_2 & d_3 \end{bmatrix} \begin{bmatrix}g_0 \\ g_1 \\ g_2\end{bmatrix} = \begin{bmatrix}d_0 g_0+d_1 g_1+d_2 g_2 \\ d_1 g_0+d_2 g_1+d_3 g_2\end{bmatrix} = \begin{bmatrix}m_1+m_2+m_3 \\ m_2 - m_3 - m_4\end{bmatrix}, (1)$

где использованы обозначения:

$m_1=(d_0-d_2)g_0 , \\ m_2=(d_1+d_2)\frac{g_0+g_1+g_2}{2} , \\ m_3=(d_2-d_1)\frac{g_0-g_1+g_2}{2}, \\ m_4=(d_1-d_3)g_2.$

На первый взгляд, последняя замена выглядит несколько бессмысленно — операций стало явно больше. Но выражения $\frac{g_0+g_1+g_2}{2}$ и $\frac{g_0-g_1+g_2}{2}$ нужно рассчитать только один раз. С учетом этого нам надо выполнить всего 4 операции умножения, в то время как в оригинальной формуле их необходимо сделать 6.
Выражение (1) перепишем еще раз:

$F(2,3)=A^T[(G g)\odot(B^T d)] , (2)$

где $\odot$ обозначает поэлементное умножение, а также используются следующие обозначения:

$B^T=\begin{bmatrix}1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1\end{bmatrix} , (3)\\ G=\begin{bmatrix}1 & 0 & 0 \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 1\end{bmatrix} , (4)\\ A^T = \begin{bmatrix}1 & 1 & 1 & 0 \\ 0 & 1 & -1 & -1\end{bmatrix} . (5)$

Выражение (2) можно обобщить на двумерный случай:

$F(2\times2,3\times3)=A^T\bigg[[G g G^T]\odot[B^T d B]\bigg] A. (6)$

Требуемое количество операций умножения для $F(2\times2,3\times3)$ сократится с $2\times2\times3\times3=36$ до $4\times4=16$ . Таким образом мы получаем вычислительный выигрыш в $\frac{36}{16}=2.25$ раза. Если визуализировать, то по сути мы, вместо раздельного вычисления свертки для каждой точки изображения, будем вычислять его сразу для блока размером $2\times2$ :

В произвольном случае для свертки с окном $r\times s$ и размером блока $m\times n$ количество требуемых умножений будет

$count = (m + r - 1)\times(n + s - 1) , (7)$

а выигрыш описывается формулой:

$k = \frac{m\times n\times r\times s}{(m + r - 1)\times(n + s - 1)} . (8)$

В пределе, при достаточно больших $inline$ и $inline$ для любой свертки достаточно всего 1 операции умножения на точку! К сожалению, увеличение размера блока ведет к быстрому увеличению накладных расходов на преобразование входного $inline$ и выходного $inline$ изображения, так что на практике обычно не используют размер блока больше, чем $4\times4$ .

Пример реализации

Для практической реализации алгоритма Винограда хотелось бы рассмотреть простейший случай — свертку с ядром $3\times3$ для блока $2\times2$ . С целью дальнейшего упрощения изложения будем также полагать, что паддинг входного изображения отсутствует, а размеры входного и выходного изображения кратны 2.

Реализация свертки, основанная на матричном умножении, будет иметь вид:

float relu(float value)
{
    return value > 0 ? return value : 0;
}

void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, 
    float beta, const float * B, int ldb, float * C, int ldc)
{
  for (int i = 0; i < M; ++i)
    for (int j = 0; j < N; ++j)
    {
      C[i*ldc + j] = beta;
      for (int k = 0; k < K; ++k)
        C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j];
    }
}

void im2col(const float * src, int srcC, int srcH, int srcW,
    int kernelY, int kernelX, float * buf)
{
  int dstH = srcH - kernelY + 1;
  int dstW = srcW - kernelX + 1;
  for (int sc = 0; sc < srcC; ++sc)
    for (int ky = 0; ky < kernelY; ++ky)
      for (int kx = 0; kx < kernelX; ++kx)
        for (int dy = 0; dy < dstH; ++dy)
          for (int dx = 0; dx < dstW; ++dx)
            *buf++ = src[((b * srcC + sc)*srcH + dy + ky)*srcW + dx + kx];
}

void convolution(const float * src, int batch, int srcC, int srcH, int srcW,
    int kernelY, int kernelX, int dilationY, int dilationX,
    int strideY, int strideX, int padY, int padX, int padH, int padW, int group,
    const float * weight, const float * bias, float * dst, int dstC, float * buf)
{
  int dstH = srcH - kernelY + 1;
  int dstW = srcW - kernelX + 1;
  int M = dstC;
  int N = dstH * dstW;
  int K = srcC * kernelY * kernelX;
  for (int b = 0; b < batch; ++b)
  {
    im2col(src, srcC, srcH, srcW, kernelY, kernelX, buf);
    gemm_nn(M, N, K, 1, weight, K, 0, buf, N, dst, N));
    for (int i = 0; i < M; ++i)
      for (int j = 0; j < N; ++j)
        dst[i*N+ j] = relu(dst[i*N + j] + bias[i]);
    src += srcC*srcH*srcW;
    dst += dstC*dstH*dstW;
  }
}

Тем, кто хочет подробно понять, что здесь происходит, необходимо обратится к моей предыдущей статье. Текущая реализация получается из предыдущей, если положить:

strideY = strideX = dilationY = dilationX = group = 1, padY = padX = padH = padW = 0.

Mодифицированный алгоритм свертки

Приведу здесь еще раз формулу (6):

$F(2\times2,3\times3)=A^T\bigg[[G g G^T]\odot[B^T d B]\bigg] A.$

Если перейти от выходного изображения размером $2\times2$ к изображению произвольного размера, то нам придется разбить его на блоки размером $2\times2$ . Для каждого такого блока из входного изображения будет образовано $(2 + 3 - 1)\times(2 + 3 - 1)=16$ значений, которые входят в 16 преобразованных $inline$ входных изображений уменьшенного вдвое размера. Затем осуществляется умножение каждой из этих 16 матриц на соответсвующую матрицу преобразованных весов $inline$ . 16 получившихся в итоге матриц преобразуются к выходному изображению $A^T\bigg[...\bigg] A$ . Ниже этот процесс нарисован на схеме:

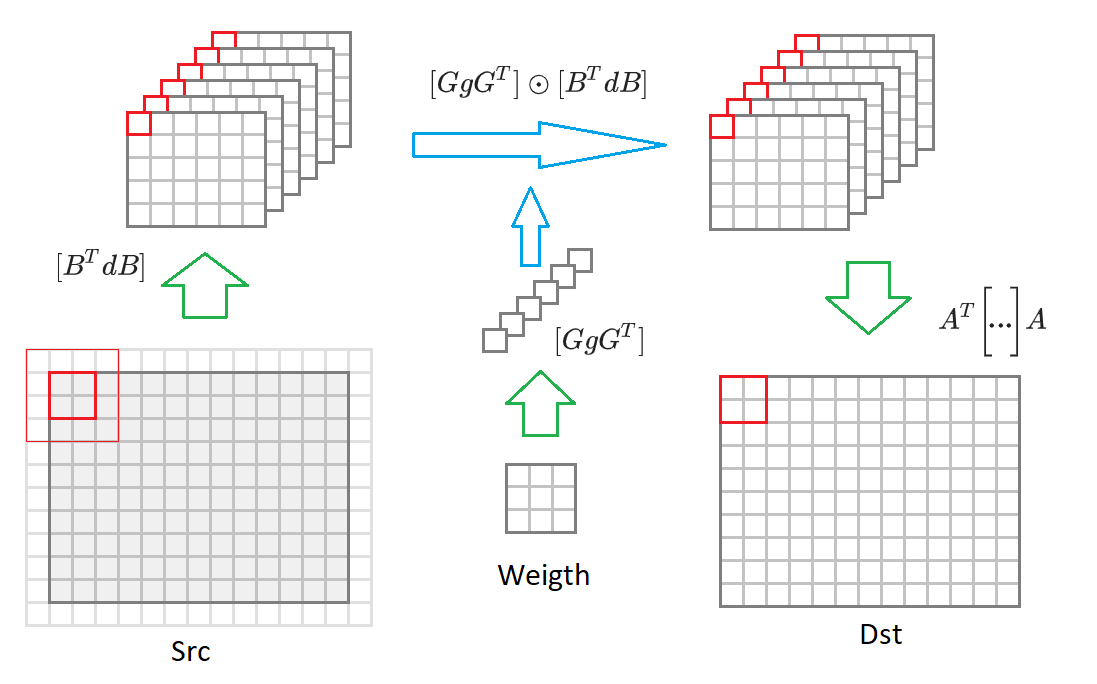
С учетом этих замечаний алгоритм свертки примет вид:

void convolution(const float * src, int batch, int srcC, int srcH, int srcW,
    int kernelY, int kernelX, int dilationY, int dilationX,
    int strideY, int strideX, int padY, int padX, int padH, int padW, int group,
    const float * weight, const float * bias, float * dst, int dstC, float * buf)
{
  const int block = 2, kernel = 3;
  int count = (block + kernel - 1)*(block + kernel - 1); // 16
  int dstH = srcH - kernelY + 1;
  int dstW = srcW - kernelX + 1;
  int tileH = dstH / block;
  int tileW = dstW / block;
  int sizeW = srcC * dstC;
  int sizeS = srcC * tileH * tileW;
  int sizeD = dstC * tileH * tileW;
  int M = dstC;
  int N = tileH * tileW;
  int K = srcC;
  float * bufW = buf;
  float * bufS = bufW + sizeW*count;
  float * bufD = bufS + sizeS*count;
  set_filter(weight, sizeW, bufW);
  for (int b = 0; b < batch; ++b)
  {
    set_input(src, srcC, srcH, srcW, bufS, sizeS);
    for (int i = 0; i < count; ++i)
      gemm_nn(M, N, K, 1, bufW + i * sizeW, K, 
        bufS + i * sizeS, N, 0, bufD + i * sizeD, N));
    set_output(bufD, sizeD, dst, dstC, dstH, dstW);
    for (int i = 0; i < M; ++i)
      for (int j = 0; j < N; ++j)
        dst[i*N+ j] = relu(dst[i*N + j] + bias[i]);
    src += srcC*srcH*srcW;
    dst += dstC*dstH*dstW;
  }
}

Количество операций, которые требуются без учета преобразований входного и выходного изображения: ~srcC*dstC*dstH*dstW*count. Далее опишем алгоритмы преобразования весов, входного и выходного изображения.

Преобразование сверточных весов

Как видно из выражения (6), над весами свертки нужно выполнить следующее преобразование: $inline$ , где матрица $inline$ определена в выражении (4). Код для такого преобразования будет иметь следующий вид:

void set_filter(const float * src, int size, float * dst)
{
  for (int i = 0; i < size; i += 1, src += 9, dst += 1)
  {
    dst[0 * size] = src[0];
    dst[1 * size] = (src[0] + src[2] + src[1])/2;
    dst[2 * size] = (src[0] + src[2] - src[1])/2;
    dst[3 * size] = src[2];
    dst[4 * size] = (src[0] + src[6] + src[3])/2;
    dst[5 * size] = ((src[0] + src[6] + src[3]) + 
        (src[2] + src[8] + src[5]) + (src[1] + src[7] + src[4]))/4;
    dst[6 * size] = ((src[0] + src[6] + src[3]) + 
        (src[2] + src[8] + src[5]) - (src[1] + src[7] + src[4]))/4;
    dst[7 * size] = (src[2] + src[8] + src[5])/2;
    dst[8 * size] = (src[0] + src[6] - src[3])/2;
    dst[9 * size] = ((src[0] + src[6] - src[3]) + 
        (src[2] + src[8] - src[5]) + (src[1] + src[7] - src[4]))/4;
    dst[10 * size] = ((src[0] + src[6] - src[3]) + 
        (src[2] + src[8] - src[5]) - (src[1] + src[7] - src[4]))/4;
    dst[11 * size] = (src[2] + src[8] - src[5])/2;
    dst[12 * size] = src[6];
    dst[13 * size] = (src[6] + src[8] + src[7])/2;
    dst[14 * size] = (src[6] + src[8] - src[7])/2;
    dst[15 * size] = src[8];
  }
}

К счастью это преобразование нужно сделать только 1 раз. Потому оно не влияет на итоговую производительность.

Преобразование входного изображения

Как видно из выражения (6), над входным изображением нужно выполнить следующее преобразование: $inline$ , где матрица $inline$ определена в выражении (3). Код для такого преобразования будет иметь следующий вид:

void set_input(const float * src, int srcC, int srcH, int srcW, 
    float * dst, int size)
{
  int dstH = srcH - 2;
  int dstW = srcW - 2;
  for (int c = 0; c < srcC; ++c)
  {
    for (int row = 0; row < dstH; row += 2)
    {
      for (int col = 0; col < dstW; col += 2)
      {
        float tmp[16];
        for (int r = 0; r < 4; ++r)
          for (int c = c; c < 4; ++c)
            tmp[r * 4 + c] = src[(row + r) * srcW + col + c];
        dst[0 * size] = (tmp[0] - tmp[8]) - (tmp[2] - tmp[10]);
        dst[1 * size] = (tmp[1] - tmp[9]) + (tmp[2] - tmp[10]);
        dst[2 * size] = (tmp[2] - tmp[10]) - (tmp[1] - tmp[9]);
        dst[3 * size] = (tmp[1] - tmp[9]) - (tmp[3] - tmp[11]);
        dst[4 * size] = (tmp[4] + tmp[8]) - (tmp[6] + tmp[10]);
        dst[5 * size] = (tmp[5] + tmp[9]) + (tmp[6] + tmp[10]);
        dst[6 * size] = (tmp[6] + tmp[10]) - (tmp[5] + tmp[9]);
        dst[7 * size] = (tmp[5] + tmp[9]) - (tmp[7] + tmp[11]);
        dst[8 * size] = (tmp[8] - tmp[4]) - (tmp[10] - tmp[6]);
        dst[9 * size] = (tmp[9] - tmp[5]) + (tmp[10] - tmp[6]);
        dst[10 * size] = (tmp[10] - tmp[6]) - (tmp[9] - tmp[5]);
        dst[11 * size] = (tmp[9] - tmp[5]) - (tmp[11] - tmp[7]);
        dst[12 * size] = (tmp[4] - tmp[12]) - (tmp[6] - tmp[14]);
        dst[13 * size] = (tmp[5] - tmp[13]) + (tmp[6] - tmp[14]);
        dst[14 * size] = (tmp[6] - tmp[14]) - (tmp[5] - tmp[13]);
        dst[15 * size] = (tmp[5] - tmp[13]) - (tmp[7] - tmp[15]);
        dst++;
      }
    }
    src += srcW * srcH;
  }
}

Количество операций, которые требуются для этого преобразования: ~srcH*srcW*srcC*count.

Преобразование выходного изображения

Как видно из выражения (6), над выходным изображением нужно выполнить следующее преобразование: $inline$ , где матрица $inline$ определена в выражении (5). Код для такого преобразования будет иметь следующий вид:

void set_output(const float * src, int size, 
    float * dst, int dstC, int dstH, int dstW)
{
  for (int c = 0; c < dstC; ++c)
  {
    for (int row = 0; row < dstH; row += 2)
    {
      for (int col = 0; col < dstW; col += 2)
      {
        float tmp[8];
        tmp[0] = src[0 * size] + src[1 * size] + src[2 * size];
        tmp[1] = src[1 * size] - src[2 * size] - src[3 * size];
        tmp[2] = src[4 * size] + src[5 * size] + src[6 * size];
        tmp[3] = src[5 * size] - src[6 * size] - src[7 * size];
        tmp[4] = src[8 * size] + src[9 * size] + src[10 * size];
        tmp[5] = src[9 * size] - src[10 * size] - src[11 * size];
        tmp[6] = src[12 * size] + src[13 * size] + src[14 * size];
        tmp[7] = src[13 * size] - src[14 * size] - src[15 * size];
        dst[col + 0] = tmp[0] + tmp[2] + tmp[4];
        dst[col + 1] = tmp[1] + tmp[3] + tmp[5];
        dst[dstW + col + 0] = tmp[2] - tmp[4] - tmp[6];
        dst[dstW + col + 1] = tmp[3] - tmp[5] - tmp[7];
        src++;
      }
      dst += 2*dstW;
    }
  }
}

Количество операций, которые требуются для этого преобразования: ~dstH*dstW*dstC*count.

Особенности практической реализации

В рассмотренном выше примере мы привели описание алгоритма Винограда для блока размером $2\times2$ . На практике чаще всего используют более продвинутый вариант алгоритма: $F(4\times4,3\times3)$ . В этом случае размером блока будет $4\times4$ , а количество преобразованных матриц — 36. Вычислительный выигрыш, согласно формуле (8) будет достигать 4. Общая схема алгоритма такая же, отличаются только матрицы алгоритмов преобразования.

Существует небольшой проект на Github, который позволяет рассчитать эти матрицы с коэффициентами для произвольного размера ядра свертки и размера блока.

Мы привели вариант алгоритма Винограда для формата изображения NCHW, но алгоритм может быть по похожей схеме реализован и для формата NHWC (подробнее об этих форматах изображения я рассказывал в предыдуще статье.

Не смотря на наличие дополнительных преобразований, основная вычислительная нагрузка в алгоритме Винограда (при его грамотном применении, конечно) все равно лежит на матричном умножении. К счастью, это стандартная операция и эффективно реализована во множестве библиотек.

Оптимизированные под разные платформы функции преобразования для алгоритма Винограда можно найти здесь.

Плюсы и минусы алгоритма Винограда

Сначала конечно плюсы:

Алгоритм позволяет в несколько раз (чаще всего в 2-3 раза) ускорить вычисление свертки. Таким образом удается вычислять свертку быстрее «теоретического» предела.
Алгоритм опирается в своей реализации на стандартный алгоритм матричного умножения.
Он может реализован для различных форматов входных изображений: NCHW, NHWC.
Размер буфера для хранения промежуточных значений меньше, чем требуется для алгоритма, основанного на матричном умножении.

Ну и куда же без минусов:

Алгоритм требует отдельной реализации функций преобразования для каждого размера ядра свертки, а также для каждого размера блока. Может быть это является одной из основных причин того, что он практически везде реализован только для свертки с ядром $3\times3$ .
С ростом размера блока, сложность реализации функций преобразования быстро растет. Поэтому практически нет реализаций с размером блока больше чем $4\times4$ .
Алгоритм накладывает жесткие ограничения на параметры свертки strideY = strideY = dilationY = dilationX = group = 1. Хотя теоретически, возможна реализация алгоритма, когда эти ограничения нарушаются, на практике она мала применима по причине низкой эффективности.
Эффективность алгоритма падает, если число входных или выходных каналов в изображении мало (это связано с затратами на конвертацию входных и выходных изображений).
Эффективность алгоритма падает для малых размеров входных изображений (получающиеся матрицы из входного изображения имеют слишком маленькие размеры, и стандартный алгоритм матричного умножения для них становится не эффективным).

Выводы

Метод вычисления свертки, основанный на алгоритме Винограда, позволяет значительно повысить вычислительную эффективность по сравнению с методом, основанном на простом матричном умножении. К сожалению, он не универсален и достаточно сложен в реализации. Для ряда частных случаев существуют более быстрые подходы, описание которых мне хотелось бы отложить для следующих статей данной серии. Жду отзывов и замечаний от читателей. Надеюсь, вам было интересно!

P.S. Этот и другие подходы реализованы мной в Convolution Framework в рамках библиотеки Simd.
Данный фреймворк лежит в основе Synet — фреймворка для запуска предварительно обученных нейронных сетей на CPU.

Теги:

Хабы: