Комментарии 40
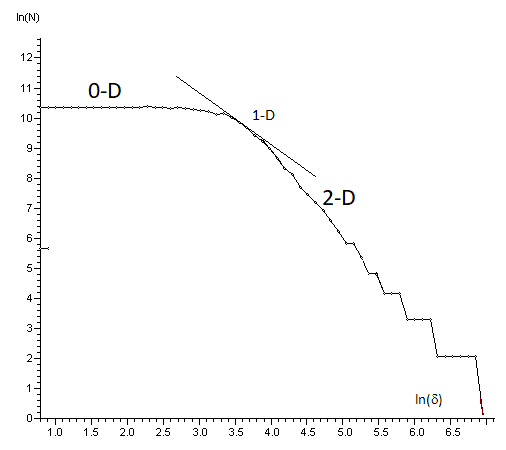
Я тоже занимался исследованием данной проблемы. Подошел с другого конца. Если случайно разбросать точки на квадрате, то издалека они видны, как нечто двумерное. Если приблизиться и смотреть в упор на одну точку, размерность равна нулю. Значит на каком-то промежуточном масштабе этот случайный набор будет иметь промежуточную геометрию, то есть образовывать подобие линий или каких-то скоплений. На этом масштабе наиболее возможны кореляции или обнаружение каких-то структур, которые можно принять за закономерность. Чтобы найти этот масштаб, надо построить график фрактальной размерности методом Миньковского. Наклон графика показывает размерность множества на масштабе «сигма»

+2
Подумаю. Так сразу не готов что-то ответить
0
Как пример — звездное небо. В целом звезды расположены более-менее случайно. Но наш мозг начинает искать какие-то линии, треугольники и созвездия, рассматривая связи определенной длинны. То есть наша нейросеть находит закономерности и обучается на случайных данных.
0
Согласен это есть. Просто если взять глобальней, есть высказывание, что: «Все принятые человеком упорядочивания, это разновидность хаоса». Я что-то все больше приближаюсь к идеи, что хаос — это локальное свойство нашего восприятия.
Ведь если посмотреть, те закономерности, которые обнаруживают нейронные сети сейчас, еще, 50 лет назад, принимались бы за случайное множество.
Мне эта теорема Эрдеша-Реньи понравилась тем, что она позволяет, после определения аналитических зависимостей исследовать остаточный ряд и, по моим предположениям, определять присутствуют ли в остаточном ряде зависимости, которые могут быть обнаружены нейронными сетями. То есть по сути проводить тест на наличие нейронных зависимостей. А если это так, то это уже мощный инструмент.
Ведь если посмотреть, те закономерности, которые обнаруживают нейронные сети сейчас, еще, 50 лет назад, принимались бы за случайное множество.
Мне эта теорема Эрдеша-Реньи понравилась тем, что она позволяет, после определения аналитических зависимостей исследовать остаточный ряд и, по моим предположениям, определять присутствуют ли в остаточном ряде зависимости, которые могут быть обнаружены нейронными сетями. То есть по сути проводить тест на наличие нейронных зависимостей. А если это так, то это уже мощный инструмент.
+1
Есть еще теория Рамсея о присутствии арифметической прогрессии в случайном множестве. Философски тоже подводит к нахождению порядка среди хаоса.
0
При игре на бирже только удача определяет, сколько времени продержится трейдер, пока не проиграет свой капитал.
Настрораживающе категоричное заявление. Оно становится верным только если под словом «биржа» подразумевать любой тотализатор (ипподром, FOREX, ставки на спортивные результаты), а не биржу акций. Для биржи акций есть тривиальная беспроигрышная стратегия — ставить на индексы и не выходить десятки лет. Среднегодовая доходность акций (~4-6%) за длительное время перекроет среднегодовую инфляцию (~2.5-3%).
0
Начну с определения игра для экономики, оно сейчас сформировалось, поэтому не судите строго. Игра — это потенциально выгодные трансакции между двумя или более субъектами на основе установленных ими правил. Эти трансакции по длительности менее длительности делового цикла самой эффективной отрасли экономики.
То есть та стратегия которую вы описали, это действия институционального характера которые свойственны инвестору.
Поэтому предполагаю, что если б написал «инвестор» вместо «трейдера» то ваше замечание было б обоснованным
То есть та стратегия которую вы описали, это действия институционального характера которые свойственны инвестору.
Поэтому предполагаю, что если б написал «инвестор» вместо «трейдера» то ваше замечание было б обоснованным
0
В первой публикации (и собственно в книге, на которую она ссылалась) приведена другая формулировка теоремы
В этой статье речь идет уже о
Это все же две разные вероятности (возможно при стремлении N к бесконечности, они и совпадают).
При бросании монеты n раз, серия из гербов длины log2(n) наблюдается с вероятностью, стремящейся к 1, при n стремящемся к бесконечности.
В этой статье речь идет уже о
При бросании монеты N раз, серия выпадения одинаковых сторон монеты подряд длины log2(n) наблюдается с вероятностью, стремящейся к 1, при N стремящемся к бесконечности.
Это все же две разные вероятности (возможно при стремлении N к бесконечности, они и совпадают).
0
Вероятности выпадения орла или решки подряд несколько раз, то есть серии симметричны. Да и модераторы Хабра просили избегать использования терминов из СССР. Так тогда термин «орел» был заменен на «герб».
Вот я и заменил формулировку «серия из гербов» на «выпадения одинаковых сторон монеты подряд». С другой стороны это переводное издание и, вполне возможно, что в оригинале была другая формулировка.
Предполагаю, что это одно и то же. Так как когда в следующее выбрасывание после первого герба выпадает снова герб, то это одинаковая сторона с предыдущим выбрасыванием
Вот я и заменил формулировку «серия из гербов» на «выпадения одинаковых сторон монеты подряд». С другой стороны это переводное издание и, вполне возможно, что в оригинале была другая формулировка.
Предполагаю, что это одно и то же. Так как когда в следующее выбрасывание после первого герба выпадает снова герб, то это одинаковая сторона с предыдущим выбрасыванием
0
Кажется естественным, что частота Мизеса по Ф.6.1 для единичного цуга из одного события должна быть 1/2.
Но подставляя w=1 и n=1 в Ф.6.1 получаем 1/4. Отчего так?
Но подставляя w=1 и n=1 в Ф.6.1 получаем 1/4. Отчего так?
0
Почему 1/4 по формуле 1/16.
0
Да, ошибся, 1/16.
Но если судить по первоисточнику, один цуг из одного события — это единичное выпадение орла.
Но если судить по первоисточнику, один цуг из одного события — это единичное выпадение орла.
0
В «Постулатах Голомба» даются условия при которых можно использовать цуги. Это связано с тем что они исследовали нормы создания псевдослучайных последовательностей. То есть последовательностей максимально неотличимых от случайных, для целей шифрования. Это следует понимать. Они исследовали цуги вида «01», «0011», «111000» и т.д. То есть переход от 0 к 1 и обратно. Их задачей, как я понял, было для ряда N найти набор цуг к каждому ряду и разбросать их по ряду а оставшиеся пустые места в ряде N заполнить случайным образом 0 и 1. То есть их серии более log(2)N не интересовали. И если образовывались то по принципу:
Разбросали цуги по ряду и в каком-то месте получилось:
000111j11110000, далее при случайном забрасывании на место j попадает 1. Тогда образовывается серия из восьми 1: 000111111110000.
Но эта серия их не интересовала.
Я когда увидел у Филатова О.В. формулы 6.1-6.3 и подставив туда log(2)N и увидел что сходится. Просто обрадовался. Так как филатовская группа математиков по сути, другими способами, решая другие задачи пришли к тому же результату, что и Эрдеш-Реньи. В общей практике, такое событие считается независимым подтверждением результатов исследования.
Тут еще следует понимать, что у Филатова исследуются частоты события log(2)N а у Эрдеша вероятности появления этого события. Но по Филатову если указанное событие должно появится, с учетом симметрии, то это означает, что вероятность его 1.
Еще очень аккуратно нужно с филатовскими формулами работать, так как симметрия их не интересовала, то есть цуги 01 и 10 считаются разными. У Эрдеша 0000 и 1111 считается совместная вероятность
Разбросали цуги по ряду и в каком-то месте получилось:
000111j11110000, далее при случайном забрасывании на место j попадает 1. Тогда образовывается серия из восьми 1: 000111111110000.
Но эта серия их не интересовала.
Я когда увидел у Филатова О.В. формулы 6.1-6.3 и подставив туда log(2)N и увидел что сходится. Просто обрадовался. Так как филатовская группа математиков по сути, другими способами, решая другие задачи пришли к тому же результату, что и Эрдеш-Реньи. В общей практике, такое событие считается независимым подтверждением результатов исследования.
Тут еще следует понимать, что у Филатова исследуются частоты события log(2)N а у Эрдеша вероятности появления этого события. Но по Филатову если указанное событие должно появится, с учетом симметрии, то это означает, что вероятность его 1.
Еще очень аккуратно нужно с филатовскими формулами работать, так как симметрия их не интересовала, то есть цуги 01 и 10 считаются разными. У Эрдеша 0000 и 1111 считается совместная вероятность
0
1. На первый взгляд, если судить по абзацу ниже (Филатов, вторая упоминающаяся работа)

один цуг единичной длины вроде должен соответствовать элементарному событию. Но если это не так, тогда применимость понятия «цуг» в нашем случае неочевидна, ее нужно исследовать отдельно. Не говоря о том, что формулы Филатова тоже нуждаются в проверке соответствия источникам.
2. Точная формулировка теоремы неясна — в первоисточнике («Парадоксы теории вероятностей» Г. Секей.) явно идет речь про последовательность гербов.

В этой статье идет другая формулировка.
Возможно, само утверждение верно, но у нас нет никаких оснований, ни прямых, ни косвенных, утверждать, что это теорема Эрдеша-Реньи.
Извините, но это подгон. Закономерность, очевидно, есть — хотя вполне возможно, что Эрдеш и Реньи не имеют к ней отношения. Но ее исследовать нужно более тщательно. Вы же торопитесь рассмотреть следствия.

один цуг единичной длины вроде должен соответствовать элементарному событию. Но если это не так, тогда применимость понятия «цуг» в нашем случае неочевидна, ее нужно исследовать отдельно. Не говоря о том, что формулы Филатова тоже нуждаются в проверке соответствия источникам.
2. Точная формулировка теоремы неясна — в первоисточнике («Парадоксы теории вероятностей» Г. Секей.) явно идет речь про последовательность гербов.

В этой статье идет другая формулировка.
При бросании монеты N раз, серия выпадения одинаковых сторон монеты подряд длины log2(N) наблюдается с вероятностью, стремящейся к 1, при N стремящемся к бесконечности.
Возможно, само утверждение верно, но у нас нет никаких оснований, ни прямых, ни косвенных, утверждать, что это теорема Эрдеша-Реньи.
Я когда увидел у Филатова О.В. формулы 6.1-6.3 и подставив туда log(2)N и увидел что сходится. Просто обрадовался.
Извините, но это подгон. Закономерность, очевидно, есть — хотя вполне возможно, что Эрдеш и Реньи не имеют к ней отношения. Но ее исследовать нужно более тщательно. Вы же торопитесь рассмотреть следствия.
0
Есть еще рисунок 2, где
Цепочка нижнего предела для log2(4)=2:
P4(2)=8/16 = 0.5; P5(2)=18/32 = 0.56; P6(2)=40/64 = 0.63; P7(2)=86/128 = 0.67
И цепочка верхнего предела:
P4(3)=4/16 = 0.25; P5(3)=10/32 = 0.31; P6(3)=22/64 = 0.34; P7(3)=50/128 = 0.39
Цепочка нижнего предела для log2(4)=2:
P4(2)=8/16 = 0.5; P5(2)=18/32 = 0.56; P6(2)=40/64 = 0.63; P7(2)=86/128 = 0.67
И цепочка верхнего предела:
P4(3)=4/16 = 0.25; P5(3)=10/32 = 0.31; P6(3)=22/64 = 0.34; P7(3)=50/128 = 0.39
0
Давайте возьмем какой-нибудь простой случай, например, N=3 и k=2 и посчитаем количество подпоследовательностей одинаковых сигналов вручную.
Итак,
000 — 2*
001 — 1
010 — 0
011 — 1
100 — 1
101 — 0
110 — 1
111 — 2*
Итого 8
*В последовательностях 000 и 111 — 2 подпоследовательности длины 2 одинаковых значений.
В таблице вижу 4.
Итак,
000 — 2*
001 — 1
010 — 0
011 — 1
100 — 1
101 — 0
110 — 1
111 — 2*
Итого 8
*В последовательностях 000 и 111 — 2 подпоследовательности длины 2 одинаковых значений.
В таблице вижу 4.
0
Наверное, мы что-то разное считаем.
Варианты комбинаций, где образуются подпоследовательности с длиной 1 — 101; 010; 001; 011; 100; 110. Итого 6 шт. Тут точно ошибка у меня стоит 2, видимо осталось от предыдущих расчетов. Сейчас исправлю.
Варианты комбинаций, где образуются подпоследовательности с длиной 2 — 001; 011; 100; 110. Итого 4 шт.
Варианты комбинаций, где образуются подпоследовательности с длиной 3 — 000; 111. Итого 2 шт.
Это и показано в таблице
Варианты комбинаций, где образуются подпоследовательности с длиной 1 — 101; 010; 001; 011; 100; 110. Итого 6 шт. Тут точно ошибка у меня стоит 2, видимо осталось от предыдущих расчетов. Сейчас исправлю.
Варианты комбинаций, где образуются подпоследовательности с длиной 2 — 001; 011; 100; 110. Итого 4 шт.
Варианты комбинаций, где образуются подпоследовательности с длиной 3 — 000; 111. Итого 2 шт.
Это и показано в таблице
0
Подождите, но вы там пишете
Я так понял, что подпоследовательности длины 3 включают в себя подпоследовательности длины 2.
Общая сумма больше чем 2^N, так как короткие цепочки находятся в сочетании с более длинными.
Я так понял, что подпоследовательности длины 3 включают в себя подпоследовательности длины 2.
0
И тогда вероятности Pn(k) рассчитывать некорректно — суммарное количество исходов превышает все пространство событий.
0
Вот это уже ближе к тому что пытаюсь рассмотреть в этом материале.
Если считать в двумерном пространстве, а если то, что приходит свыше 2^n, это из других пространств и оно пересекается с длинными цепочками? То есть аналог многомерной вероятности. И там законы Бернулли и комбинаторики уже не кажутся такими простыми.
Но усложним задачу.
Что будет считаться случайным рядом в кубитовом исчислении.
Будет ли считаться цепочка из 4-х выпадений {1А+В+},{1А-В+},{1А+В-},{1А-В-}, как мы сейчас считаем, по аналогии, 1111, с битовым, последовательно одинаковой. Или однозначным рядом будет только {1А+В+},{1А+В+},{1А+В+},{1А+В+}.
Вот одна из причин, почему цепочку n=log2(N) интересной. Так как на эту цепочку ссылаются множество источников, но откуда этот порог взялся пока не пойму
Если считать в двумерном пространстве, а если то, что приходит свыше 2^n, это из других пространств и оно пересекается с длинными цепочками? То есть аналог многомерной вероятности. И там законы Бернулли и комбинаторики уже не кажутся такими простыми.
Но усложним задачу.
Что будет считаться случайным рядом в кубитовом исчислении.
Будет ли считаться цепочка из 4-х выпадений {1А+В+},{1А-В+},{1А+В-},{1А-В-}, как мы сейчас считаем, по аналогии, 1111, с битовым, последовательно одинаковой. Или однозначным рядом будет только {1А+В+},{1А+В+},{1А+В+},{1А+В+}.
Вот одна из причин, почему цепочку n=log2(N) интересной. Так как на эту цепочку ссылаются множество источников, но откуда этот порог взялся пока не пойму
0
А вот здесь я неправ, извините. События не являются независимыми, поэтому сумма вероятностей по k и не обязана быть равной 1.
Лучше добавить k >= N/2 к условию k < N в формуле Pn(k) — так будет наглядней.
Лучше добавить k >= N/2 к условию k < N в формуле Pn(k) — так будет наглядней.
0
Да, разное.
В тексте
Вы считаете эти комбинации, причем k означает «ровно k и не более».
Я ориентировался на подпись к рис. 2
и считал именно количество вариантов субрядов одинаковых сигналов длиной k, причем полагал, что субряд длиной k может являться частью субряда длиной k+1.
В тексте
На рисунке 2 представлено распределение вариантов цепочек из N сигналов в которых существуют ряды из субрядов длиной k
Вы считаете эти комбинации, причем k означает «ровно k и не более».
Я ориентировался на подпись к рис. 2
Рис. 2. Число возможных вариантов субряда из k одинаковых сигналов, в последовательности из N значений.
и считал именно количество вариантов субрядов одинаковых сигналов длиной k, причем полагал, что субряд длиной k может являться частью субряда длиной k+1.
0
Извините. Там в последнем комменте кто-то затеял свою игру. Мы с ним доиграем и я отвечу
0
Не забыл про Ваши вопросы. Эту задачу решал. Решил ее. Потом проверил есть ли уже подобное решение, оказалось, что ее в 2008 году решил наш соотечественник. Вот здесь это зафиксировано oeis.org/A140993. Сверстаю публикацию, в которой напишу что увидел.
0
*В последовательностях 000 и 111 — 2 подпоследовательности длины 2 одинаковых значений.
Исследовал такой подход. Отказался, так как пришел к предпосылке, что такой подход предполагает декомпозицию больших данных на составляющие из меньшего объема. То есть, существуют шансы потерять более общие свойства большого ряда
0
Раз вышла такая дискуссия, то позволю себе сделать выводы по некоторым наблюдениям. Есть какие-то устоявшиеся правила ведения таких дискуссий. И когда, одна из сторон, опирается, в своей аргументации, на проявление эмоций другой стороной и после этого предлагает выводы. То тем самым она подтверждает факт, что это проявление эмоций она использовала для получения своих выводов.
Лично я, нигде не встречал, ни в каких правилах и нормах, что утверждения по которому: «Генерация эмоций человеком, является основанием предположить, что его выводы ненадежны» состоятельно.
В любой дискуссии и, в том числе нашей, использование любого высказывания имеет обоюдоострое отношение. Мне не составляет труда доказать, что в ваших аргументах присутствует эмоция «сомнение». И если вы, используете опору на наличие эмоций, как один из аргументов, значит этот же факт можно использовать и по отношению к вашим рассуждениям. Но, уже ко всем представленным Вами, так как я указал, что это относится к одному из событий.
И в добавок, утверждение: «Генерация эмоций человеком, является основанием предположить, что его выводы ненадежны», вызовет, из собственного опыта, отвержения, как минимум у половины человечества — самой прекрасной.
Ну, а по сути дискуссии, я, естественно, отработаю, причины на которых возникли ваши утверждения. Хотя изменить интервалы надежности, используемые мной в этом анализе, они не смогли. Но в исследовании по данному аспекту помогли.
Лично я, нигде не встречал, ни в каких правилах и нормах, что утверждения по которому: «Генерация эмоций человеком, является основанием предположить, что его выводы ненадежны» состоятельно.
В любой дискуссии и, в том числе нашей, использование любого высказывания имеет обоюдоострое отношение. Мне не составляет труда доказать, что в ваших аргументах присутствует эмоция «сомнение». И если вы, используете опору на наличие эмоций, как один из аргументов, значит этот же факт можно использовать и по отношению к вашим рассуждениям. Но, уже ко всем представленным Вами, так как я указал, что это относится к одному из событий.
И в добавок, утверждение: «Генерация эмоций человеком, является основанием предположить, что его выводы ненадежны», вызовет, из собственного опыта, отвержения, как минимум у половины человечества — самой прекрасной.
Ну, а по сути дискуссии, я, естественно, отработаю, причины на которых возникли ваши утверждения. Хотя изменить интервалы надежности, используемые мной в этом анализе, они не смогли. Но в исследовании по данному аспекту помогли.
0
Дело не в том, что вы обрадовались, дело в том, что вы использовали формулы без должного обоснования. В моем комментарии сначала идут 2 абзаца с фактами.
Я вот, например, до сих пор не понимаю, применимо ли понятие цуга к данному случаю или нет. Если один цуг единичной длины — элементарное событие (выпадение орла), тогда формула Ф.6.1 должна давать 1/2 для n=1, w=1.
Если же речь идет о выпадении монеты любой стороной, тогда для цуга единичной длины Ф.6.1. должна выдать 1.
У нас же получается 1/16.
Если же цуг — это что-то совершенно другое, тогда непонятно, а применимы ли эти формулы вообще.
С формулировкой теоремы тоже неясно — эти 2 варианта не эквивалентны.
Вероятность встретить подпоследовательность из k одинаковых значений подряд в 2 раза выше, чем из вероятность встретить подпоследовательность из k орлов подряд.
Вы пишете
Я уже вставил цитату из перевода, чтобы было ясно, что во всем абзаце речь идет именно о выпадении гербов и ошибку перевода можно исключить.
Плюс в предыдущей статье я приводил ссылку на пост из ЖЖ Орел или решка? Там автор подсчитал вероятности выпадения последовательности одинаковых значений и проверил это моделированием.
Еще раз приведу цитату оттуда
И еще одна цитата
Т.е. по-видимому, встретить последовательность длиной log2(n) или больше — порядка 50%, а не 100%. Это, конечно, не непреложная истина, но утверждение, явно заслуживающее проверки.
Я вот, например, до сих пор не понимаю, применимо ли понятие цуга к данному случаю или нет. Если один цуг единичной длины — элементарное событие (выпадение орла), тогда формула Ф.6.1 должна давать 1/2 для n=1, w=1.
Если же речь идет о выпадении монеты любой стороной, тогда для цуга единичной длины Ф.6.1. должна выдать 1.
У нас же получается 1/16.
Если же цуг — это что-то совершенно другое, тогда непонятно, а применимы ли эти формулы вообще.
С формулировкой теоремы тоже неясно — эти 2 варианта не эквивалентны.
Вероятность встретить подпоследовательность из k одинаковых значений подряд в 2 раза выше, чем из вероятность встретить подпоследовательность из k орлов подряд.
Вы пишете
Вот я и заменил формулировку «серия из гербов» на «выпадения одинаковых сторон монеты подряд». С другой стороны это переводное издание и, вполне возможно, что в оригинале была другая формулировка.
Предполагаю, что это одно и то же.
Я уже вставил цитату из перевода, чтобы было ясно, что во всем абзаце речь идет именно о выпадении гербов и ошибку перевода можно исключить.
Плюс в предыдущей статье я приводил ссылку на пост из ЖЖ Орел или решка? Там автор подсчитал вероятности выпадения последовательности одинаковых значений и проверил это моделированием.
Еще раз приведу цитату оттуда
Ого, то есть получить семь орлов или решек подряд при ста подбрасываниях не только вполне вероятно, но шансов что выпадет семь или больше вообще около 54%
И еще одна цитата
Если бросать монетку не сто раз, а больше, то будет увеличиваться и вероятность получить все более длинную максимальную последовательность орлов или решек подряд. Правда, вероятность эта растет крайне медленно. Если посмотреть на графики, то видно, что даже в случае 100000 подбрасываний за шанс фифти-фифти пролезает только последовательность длиной 17.
Т.е. по-видимому, встретить последовательность длиной log2(n) или больше — порядка 50%, а не 100%. Это, конечно, не непреложная истина, но утверждение, явно заслуживающее проверки.
0
Давайте так. На сколько я смог проверить законы комбинаторики не нарушаются. То есть если вот для этой цитаты «Если посмотреть на графики, то видно, что даже в случае 100000 подбрасываний за шанс фифти-фифти пролезает только последовательность длиной 17.» Если авторы не ошиблись в расчетах, то их утверждение остается верным. Так же и с остальными примерами.
По поводу орлов, если бы Эрдеш имел бы ввиду орлов, то он бы поставил вероятность 0,5, исключая симметрию, но он поставил 1, то есть учитывал серии и по орлам и по решкам. Венгерский язык считается сложнее русского, так откуда-то всплыла инфа. Поэтому и допускаю неточность перевода.
По цугам. Они искали псевдослучайный ряд максимально подобный случайному. И поиск шел, насколько я понял, как поиск минимально необходимых требований для получения этого ряда, отсюда, мое предположение, что количеством серий, сериями длиннее минимально необходимой они не заморачивались. Они достаточно сильно опирались на свойства волны. Поэтому для коротких рядов их результаты неприменимы. Как понять волну по одной сотой практически невозможно, так и к коротким последовательностям их результаты. Вот из таких условий и попробовал применить их результаты.
По поводу орлов, если бы Эрдеш имел бы ввиду орлов, то он бы поставил вероятность 0,5, исключая симметрию, но он поставил 1, то есть учитывал серии и по орлам и по решкам. Венгерский язык считается сложнее русского, так откуда-то всплыла инфа. Поэтому и допускаю неточность перевода.
По цугам. Они искали псевдослучайный ряд максимально подобный случайному. И поиск шел, насколько я понял, как поиск минимально необходимых требований для получения этого ряда, отсюда, мое предположение, что количеством серий, сериями длиннее минимально необходимой они не заморачивались. Они достаточно сильно опирались на свойства волны. Поэтому для коротких рядов их результаты неприменимы. Как понять волну по одной сотой практически невозможно, так и к коротким последовательностям их результаты. Вот из таких условий и попробовал применить их результаты.
0
В Кормене («Алгоритмы. Построение и анализ» ) в разделе 5.4.3 Последовательности выпадения орлов показывается, что мат. ожидание последовательности орлов длиной c*log2(n) равно 1/n^(c-1) при n, стремящимся к бесконечности.
Т.е. в среднем мы должны встретить одну последовательность длиной log2(n).
Т.е. в среднем мы должны встретить одну последовательность длиной log2(n).
+1
Можете дать ссылочку на Кормене («Алгоритмы. Построение и анализ» )
0
НЛО прилетело и опубликовало эту надпись здесь
Тут прилетел вот такой комент. Как и обещал автору, я его опубликовал. Ответ у меня готов. Это будет чистая математика, понятная 95% хабравцам. Опубликую его 15.08.2019 в 20-00 МСК.
Так как меня тут немного провоцируют, то хочется получить приз. Ставки можете сделать сверху справа. Стрелка вверх, за то, что ответ будет эффективным, стрелка вниз, ни то ни се.
Делайте свои ставки господа. Проигрыша никакого, если ответ не устроит, каждый сможет забрать свою ставку на представленном ответе.
До 15.08 отвечать на комменты не буду, работу нужно работать.
Так как меня тут немного провоцируют, то хочется получить приз. Ставки можете сделать сверху справа. Стрелка вверх, за то, что ответ будет эффективным, стрелка вниз, ни то ни се.
Делайте свои ставки господа. Проигрыша никакого, если ответ не устроит, каждый сможет забрать свою ставку на представленном ответе.
До 15.08 отвечать на комменты не буду, работу нужно работать.
0
1. Биноминальное распределение определяет общее количество соотношений значений в бинарном ряде случайного процесса. И к рассматриваемому в материале вопросу: о внутренней структуре бинарного ряда и возможности составления оценок о степени внутренних связей внутри ряда, имеет достаточно далекое отношение.
2. Предполагаю, что достаточно квалифицированно понимаю, какие последствия могут быть, если та теорема, Эрдеша-Реньи, основывается на каких-то оригинальных основах и имеет место быть. Под неоригинальными основами подразумеваю, ну, допустим простое наблюдение за данными ряда. Эрдеш был признан талантливым человеком и Реньи – это человек, в честь которого названа одна из видов информационных энтропий. И когда с их именем связывают цепочку n = log2(N), длина которой является равной величине, необходимой, чтобы зафиксировать все значения ряда N в битах. И утверждается, что эта цепочка, связана с ключевыми признаками случайного ряда, и это всего лишь три строчки в научно-популярном издании 30 летней давности, то срабатывают все механизмы внимания, которые есть.
3. Практический пример.
Возьмем ряд попроще, в 9 единиц, так как он уже считался. Ряд аналогичный Вашему примеру имеет вид:
1 1 1 0 0 0 1 1 1
Называем, источником информации А, теорему Эрдеша и из нее следует, что вероятностью близкой к 1 этот ряд случаен: Р(А) = 1.
Источником информации В, возьмем таблицу рисунка 2. Из нее следует, что вероятность того события, что случайный ряд не имеет субрядов длиной 1 ед.:
Р(В) = (2^9 – 470)/2^9 = (512-470)/512 = 42/512.
Доверительные интервалы опустим и не будем их вводить в рассуждения.
По этим рассуждениям следует, что:
Р(Случ) = Р(А)* Р(В) = 1* 42/512 = 42/512
Такая вероятность, того, что ряд:
1 1 1 0 0 0 1 1 1
является случайным, не противоречит здравому смыслу.
2. Предполагаю, что достаточно квалифицированно понимаю, какие последствия могут быть, если та теорема, Эрдеша-Реньи, основывается на каких-то оригинальных основах и имеет место быть. Под неоригинальными основами подразумеваю, ну, допустим простое наблюдение за данными ряда. Эрдеш был признан талантливым человеком и Реньи – это человек, в честь которого названа одна из видов информационных энтропий. И когда с их именем связывают цепочку n = log2(N), длина которой является равной величине, необходимой, чтобы зафиксировать все значения ряда N в битах. И утверждается, что эта цепочка, связана с ключевыми признаками случайного ряда, и это всего лишь три строчки в научно-популярном издании 30 летней давности, то срабатывают все механизмы внимания, которые есть.
3. Практический пример.
Возьмем ряд попроще, в 9 единиц, так как он уже считался. Ряд аналогичный Вашему примеру имеет вид:
1 1 1 0 0 0 1 1 1
Называем, источником информации А, теорему Эрдеша и из нее следует, что вероятностью близкой к 1 этот ряд случаен: Р(А) = 1.
Источником информации В, возьмем таблицу рисунка 2. Из нее следует, что вероятность того события, что случайный ряд не имеет субрядов длиной 1 ед.:
Р(В) = (2^9 – 470)/2^9 = (512-470)/512 = 42/512.
Доверительные интервалы опустим и не будем их вводить в рассуждения.
По этим рассуждениям следует, что:
Р(Случ) = Р(А)* Р(В) = 1* 42/512 = 42/512
Такая вероятность, того, что ряд:
1 1 1 0 0 0 1 1 1
является случайным, не противоречит здравому смыслу.
0
НЛО прилетело и опубликовало эту надпись здесь
Эту задачу решал. Решил ее. Потом проверил, есть ли уже подобное решение. Оказалось, что ее в 2008 году решил наш соотечественник. Вот здесь это зафиксировано oeis.org/A140993.
0
Подискутируем. А то я уже думал что это робот сочинил
0
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Белый шум рисует черный квадрат. Часть 2. Решение