Комментарии 63
Во-первых, там ряд, он бесконечен.
Во-вторых, косинус в зависимости от аргумента может принимать значения от -1 до 1. Следовательно, сумма может быть и бесконечностью, то есть ряд может и не сойтись.
Более того, отдельная задача доказать, что эта сумма имеет амплитуду равную 2 и не более.
А вообще вы в чем-то правы. Косяк в статье. Функция должна начинаться с n=0, то есть cos(3^0 x pi)/2^0, которая дает дополнительную 1.
Смотри Вики: https://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%92%D0%B5%D0%B9%D0%B5%D1%80%D1%88%D1%82%D1%80%D0%B0%D1%81%D1%81%D0%B0
Самое интересное — график так и не показали, а в Википедии он есть (Функция Вейерштрасса).
Сама функция там кстати задана немного в другом виде.
Это увеличение количества суммируемых членов? Как его сделали плавным?
Исаак Ньютон изначально рассматривал прямую, проходящую через эту точку и соседнюю точку кривойИзвестную как секущая :)
Затем он сдвигал эту соседнюю точку всё ближе и ближе, пока наклон прямойОна же — касательная.кривой
не становился равным градиенту кривой.Тогда уж и здесь — наклону.
С производными много приколов. Возьмите функцию exp(-1/x²), при x=0 доопределим её нулевым значением (чтоб гладкая была).
Попробуйте построить ряд Тейлора для неё в окрестности 0, это забавно.
P.S. Нет-нет-нет. Надо будет обязательно перечитать. Забыл. Но, сначала, следует хорошенько подумать самому. Математика тем хороша, что, если рассуждаешь логично, то, в итоге, приходишь к правильному результату. Так можно многое вывести. Надо, только, знать, что вспоминать.
Со словом "гладкая" стоит обращаться поаккуратнее — обычно под гладкостью подразумевается бесконечная дифференцируемость.
Получившаяся геометрическая форма была непрерывной, но не имела производных
Тут или с переводом что-то не то, либо надо пояснить что такое производная геометрической формы.
Constructed by taking an equilateral triangle, then adding three smaller triangles to each side, and continuing to do so indefinitely, it was a geometric shape that was continuous but had no derivatives.Созданное путём добавления к каждой из сторон равностороннего треугольника треугольника меньшего размера и повторения этих шагов до бесконечности оно было непрерывной кривой, не имевшей производной.
И да, в математике слово форма имеет вполне опреденный смысл, это не всегда shape.
At the end of the 19th century, Swedish mathematician Helge von Koch had become interested in the idea of non-smooth functions, but he wanted to see their shape.
Тут или с переводом что-то не то, либо надо пояснить что такое производная геометрической формы.
Очевидно, имелась в виду касательная.
Свойства функции следовали из ряда чисто аналитически.
А куда потратить силы на более полезное…
То что из формулы не понятно почему нет производной — существенный недостаток этой статьи. Смысл в том, что ряд cos(3^n pi x)/(2^n) сходится в любой точке x, а если вы возьмёте производную по x, то 3^n выскочит и ряд сходится уже перестанет.
Амстердамская Фондовая Биржа считается самой старой в мире. Она была основана в 1602 году [...] и первая начала торговать ценными бумагами.https://ru.wikipedia.org/wiki/Амстердамская_фондовая_биржа
Ещё пара вкусняшек.
… у линии может быть несколько неровных кусков, но всегда есть несколько частей, которые являются «гладкими»… аргументация была построена на том «интуитивно очевидном» факте, что непрерывная кривая имеет части, на которых она увеличивается, уменьшается или остаётся плоской...
Окей, пусть у нас функция даже действительно возрастает на каком-нибудь отрезке, то есть по-простому: всякий раз когда одна точка правее другой — функция в ней выше чем в другой. Означает ли это, что функция возрастает плавно? То есть что у неё есть таки производная?
Сразу понятно, что по-прежнему могут быть "изломы", скажем если функция равна x при x<0 и 2x при x>0, то в нуле производная не будет существовать, а будет "где-то между 1 и 2".
Вот как говорят о верхних пределах, нижних, правых, левых, правых верхних, правых нижних, левых верхних, левых нижних — так можно и о производных говорить, потому что они тоже пределы.
Причём из этих 9 видов пределов (в частности, производных) те 6 которые со словом "верхние" или "нижние" всегда существуют или бесконечны, что удобно. В частности, ситуацию, когда производной нет, удобно описывать в терминах четырёх "производных чисел", которые есть соответственно верхняя правая, верхняя левая, нижняя правая и нижняя левая производные, и которые всегда существуют.
В нашем примере два правых производных числа равны 2, а два левых равны 1.
Можно также замутить функцию, которая будет бесконечно расти в какой-нибудь точке, скажем как у кубического корня в нуле. Касательная получается вертикальной, кривая при этом остаётся плавной, но актуальная бесконечность, как всегда, оставляет неприятный осадок.
Итак, сколько может быть таких "плохих" точек, где конечной производной нет, у возрастающей функции? Их может быть бесконечно много, их может быть несчётно много, как у другого небезызвестного фрактальчика — чёртовой лестницы. Собственно, точек, в которых производная равна плюс бесконечности, может быть достаточно, чтобы весь рост функции происходил только в них!
Однако ж нет, не может быть так, чтобы у возрастающей функции ни в одной точке не было конечной производной. Более того, "совокупная длина" "плохих" точек всегда будет равна нулю (теорема Лебега). Теорема трудная, и чтобы такое сочинить — нужно было научиться измерять "длину" (меру) множества, иначе она не сформулируется. То есть Канторова лестница — это худшее, что может случиться. Тут интуиция не подвела, если функция возрастает — то почти везде она возрастает плавно.
Теорему Лебега о дифференцировании монотонных функций можно сильно обобщить на вообще произвольные функции, не обязательно возрастающие, если начать смотреть на вышеупомянутые производные числа.
Из теоремы Лебега видно, что возрастающая функция не может бесконечно быстро возрастать на слишком большом количестве точек. Иначе она слишком быстро возрастёт.
Так вот, монотонность тут ни при чём, то же самое верно вообще для любых функций :)
Даже если ты функция Вейерштрасса, или даже если ты функция Дирихле, разрывная в каждой точке, твоя производная по-прежнему не может быть плюс бесконечностью в сколь-нибудь большом числе точек.
Несмотря на впечатление, создаваемое графиком, в большинстве точек у функции Вейерштрасса не существует ни конечной, ни бесконечной производной.
Более того, у абсолютно любой функции в большинстве точек может быть только три случая:
- Существует конечная производная.
- Всё плохо и все четыре производных числа растопырило в соответственные бесконечности: верхние равны плюс бесконечности, а нижние — минус бесконечности.
- Как у функции Дирихле в иррациональных точках: два производных числа "по диагонали" (скажем, левое верхнее и правое нижнее) конечны и равны между собой (у функции Дирихле — нулю), а из двух "по другой диагонали" то, которое верхнее, плюс бесконечность, а то, которое нижнее — минус бесконечность.
Всё остальное — редкие патологии. Теорема Лебега из этой "альтернативы" выводится тривиально. Это так называемая теорема Данжуа-Юнга-Сакса, она же "соотношения Данжуа".
Вот. Меня в своё время нехило штырило с этих фактов.
Простая оценка для сталкивающейся частицы, движущейся со скоростью света дает область,
в которой происходит соударение, значительно меньше размеров (электронной оболочки) атома.
Я не математик, но согласно Википедии, функция, представляющая ряд вида
\sum _{{n=0}}^{\infty }b^{n}\cos(a^{n}\pi x),
не имеет производной при условии
ab>3/2\pi +1,
что, очевидно, не выполнено для приведенного выше примера.
Очень люблю математику но редко попадает под руку что то "популярное". Спасибо за статью!
Спасибо за хороший перевод отличной статьи.
Редко в последнее время на гиктаймсе можно разглядеть качественный тематический контент в потоке гнилого щитпостинга некоторых хорошо известных пользователей.
Математический институт Клэя предложил премию в 1 миллион долларов любому, кто докажет, что эти уравнения всегда имеют гладкие решения — или найдёт пример обратного.
О, как!.. Но ведь «гладкие решения» — это свойство глубокой симметрии мира, о которой мы лишь подозреваем. Наблюдаемая картина мира противоречит этим подозрениям. Мы маниакально продолжаем противопоставлять, например, жизнь и смерть. Хотя на самом деле следует противопоставлять рождение и смерть, где сама жизнь и есть «гладкое решение» и без всякой математики. Так, что, где мой миллион!?..
там рассматривается и эта функция, и ещё много чего подобного
Тоже отличные конструкции
Так, не пойму, почему у этой функции нет производной?
Берем производную по известным правилам, получаем сумму синусов с коэффициентами. В нуле производная будет 0. В остальных точках что-то еше
Правило взятия производной от суммы не всегда работает для бесконечных рядов.
А с чего вы взяли, что ряд из производных сходится? Исходный-то ряд мажорируется убывающей геометрической прогрессией со знаменателем 1/2, а вот для производных того же самого сказать не получится — там знаменатель получается равен 3/2.
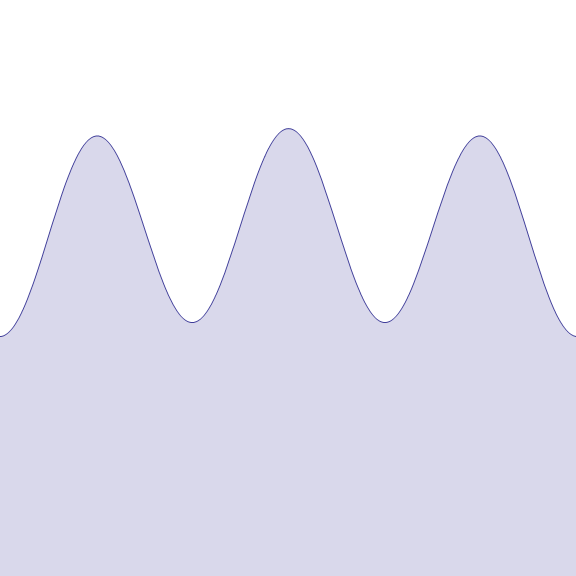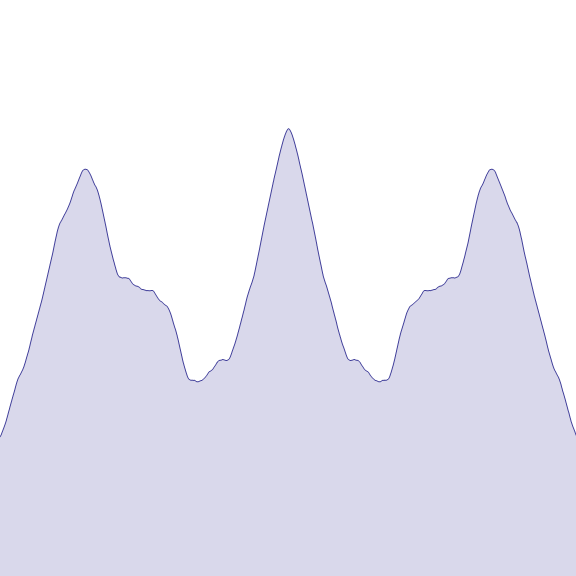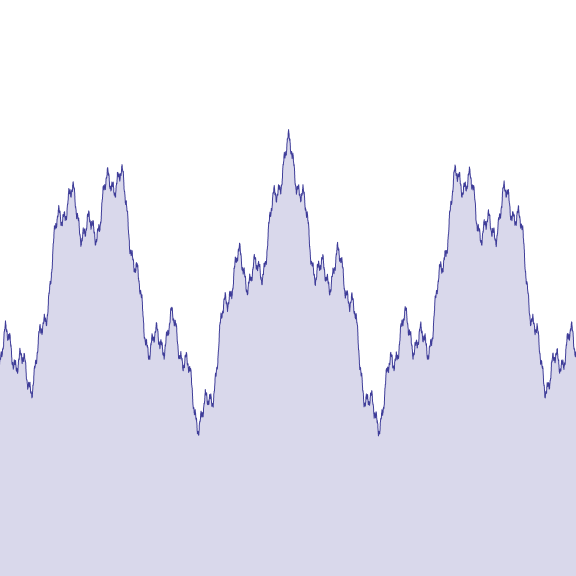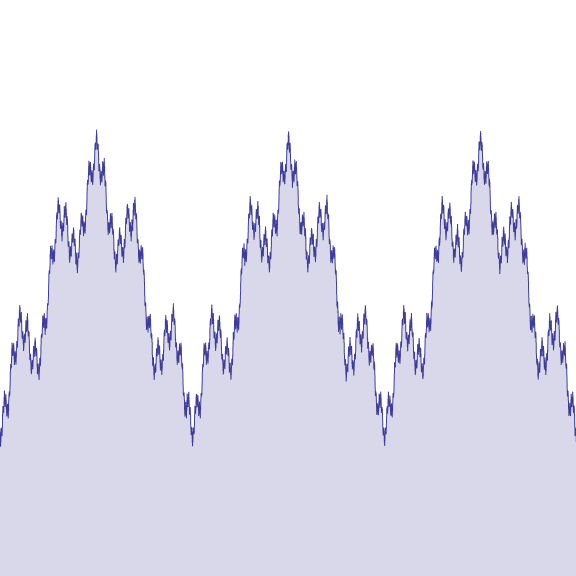
Прекрасные чудовища математики