Комментарии 40
Зря они взялись за столь сложную задачу. К вечеру обязательно найдут подвох в логическом выводе. Лучше бы разбили на квадраты. Цивилизация уже давно пользуется квадратами, но не может сделать из них сферу. {1.04!}
Интерактивна модель понравилась. Можно смело на конкурс визуальных иллюзий отправлять.
Интерактивна модель понравилась. Можно смело на конкурс визуальных иллюзий отправлять.
+9

Где я могу забрать награду?
+4
Лучше бы разбили на квадраты. Цивилизация уже давно пользуется квадратами, но не может сделать из них сферу.
+1
Не лень вам было рисовать?
Статья первоапрельская, мой комментарий тоже шуточный. Ваш ответ немного запоздал :)
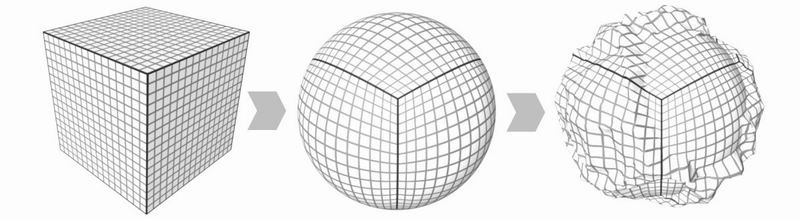
PS: А в чем смысл мятого шарика?
Статья первоапрельская, мой комментарий тоже шуточный. Ваш ответ немного запоздал :)
PS: А в чем смысл мятого шарика?
0
Нерегулярные разбиения не очень интересны.
0
В трёхмерном евклидовом пространстве существует всего пять правильных многогранников. Додекаэдр составлен из пятиугольников. Гексасфера была бы составлена из шестиугольников, если бы существовала.
+3
C 1 апреля!
+12
ммм… но ведь тэга-то нет…
-1
Тега нет, а Евклидова геометрия есть. Потому построить сферу из правильных шестиугольников невозможно.
+21
Это в официальной зашоренной науке невозможно. Учитесь смотреть на мир шире — для начала хоть бы сами попробовали построить, а потом уже говорили «невозможно».
+9
Но ещё есть же неевклидова геометрия — что сфера построена в евклидовом пространстве, нигде не сказано :)
0
А Гагарин-то не знал


+15
А не шутка?
Я знаю «гексосферу» с четырьмя квадратами по экватору.
Я знаю «гексосферу» с четырьмя квадратами по экватору.
0
Как бы мне хотелось, чтобы это было правдой :(
+3
Они так через годик и «пи» уточнить возьмутся… :)
+4
Если б было возможно — давно уже бы сделали такой футбольный мяч…
0
С футбольные мячи так и шьют по старинным лекалам, без компУтеров? :-)
0
То же мне новость…


+5
нет-нет, у тебя там чуть выше и правее центра пентагон!
+9
Но есть нюанс:


+8
Меня на Гике сегодня подловили 2 раза. Причём развод с гексасферой мне стоил инвайта :)
+1
Так сколько у них получилось в итоге-то правильных шестиугольников, чтобы описать/вписать из/в них сферу? Получен патент, поди.
0
0
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Публикации
Изменить настройки темы
Гексасфера: прорыв в полиэдральной геометрии