Комментарии 398
Стандартный математик скажет, что решения не существует.
Даже если три точки лежат на одной прямой?
А что скажет программист?
…
И дальше постарается найти решение, которое меньше всего отклонится от заданных равенств.
Но это уже другая задача из немного другой области математики.
ТЗ нужно утверждать предварительно, чтобы не было такого.
+2
следовательно, (в общем случае) решения этой системы не существует
+7
Математик скажет, что у переопределенных систем (СЛАУ) нет точного решения в общем случае.
Автор в статье привел приближенное решение, причем одно из...
Мне вот к примеру нравится другое:
[A^T · A] · x = A^T · b
безо всяких разложений в ряды преобразуется домножением на [A^T · A]^(-1)
[A^T · A]^(-1) · [A^T * A] · x = [A^T · A]^(-1) · A^T · b
получаем
x = [A^T · A]^(-1) · A^T · b
А еще можно ввести ковариационную матрицу, если статистики по разным искомым переменным отличаются друг от друга.
Автор в статье привел приближенное решение, причем одно из...
Мне вот к примеру нравится другое:
[A^T · A] · x = A^T · b
безо всяких разложений в ряды преобразуется домножением на [A^T · A]^(-1)
[A^T · A]^(-1) · [A^T * A] · x = [A^T · A]^(-1) · A^T · b
получаем
x = [A^T · A]^(-1) · A^T · b
А еще можно ввести ковариационную матрицу, если статистики по разным искомым переменным отличаются друг от друга.
0
Офигенно!
Я долго был уверен, что панический ужас, возникающий при взгляде на любые формулы, и необходимость разжевывать все самому себе на пальцах, хомячках и попугаях — это свидетельство исключительной такой персональной тупости, а остальным, мол, достаточно бросить взгляд и все понять. Почитав Фейнмана, немного успокоился, но ваш пример еще покруче (где Фейнман, а где мы, конечно).
Я долго был уверен, что панический ужас, возникающий при взгляде на любые формулы, и необходимость разжевывать все самому себе на пальцах, хомячках и попугаях — это свидетельство исключительной такой персональной тупости, а остальным, мол, достаточно бросить взгляд и все понять. Почитав Фейнмана, немного успокоился, но ваш пример еще покруче (где Фейнман, а где мы, конечно).
+14
Возможно общеизвестно и прошу простить, но что именно Вы прочли у Фейнмана?
0
"Вы, конечно, шутите, мистер Фейнман") Не то чтобы он признавался там в том же самом, но я нашел для себя какие-то похожие ощущения — необходимость иметь перед глазами наглядный пример и т.д.
0
Actually, there was a certain amount of genuine quality to my guesses.
I had a scheme, which I still use today when somebody is explaining
something that I'm trying to understand: I keep making up examples. For
instance, the mathematicians would come in with a terrific theorem, and
they're all excited. As they're telling me the conditions of the theorem, I
construct something which fits all the conditions. You know, you have a set
(one ball) — disjoint (two balls). Then the balls turn colors, grow hairs,
or whatever, in my head as they put more conditions on. Finally they state
the theorem, which is some dumb thing about the ball which isn't true for my
hairy green ball thing, so I say, "False!"
I had a scheme, which I still use today when somebody is explaining
something that I'm trying to understand: I keep making up examples. For
instance, the mathematicians would come in with a terrific theorem, and
they're all excited. As they're telling me the conditions of the theorem, I
construct something which fits all the conditions. You know, you have a set
(one ball) — disjoint (two balls). Then the balls turn colors, grow hairs,
or whatever, in my head as they put more conditions on. Finally they state
the theorem, which is some dumb thing about the ball which isn't true for my
hairy green ball thing, so I say, "False!"
+1
Гораздо лучше, чем в "Вы, конечно, шутите, мистер Фейнман", увидеть силу таланта Фейнмана в объяснении сверхсложных вещей на пальцах можно в книге "КЭД — странная теория света и вещества (Библиотечка ''Квант'' 66)".
Попробуйте, и не пожалеете.
Там, не побоюсь этого слова, настолько элегантные модели и аналогии, что чтение сравнимо с ощущениями от "Balvenie Doublewood".
И хоть квантовая электродинамика нам в большинстве случаев в практике не пригодится, всё-таки оцените и восхититесь мощью разума этого Учёного.
Попробуйте, и не пожалеете.
Там, не побоюсь этого слова, настолько элегантные модели и аналогии, что чтение сравнимо с ощущениями от "Balvenie Doublewood".
И хоть квантовая электродинамика нам в большинстве случаев в практике не пригодится, всё-таки оцените и восхититесь мощью разума этого Учёного.
+2
Вопросы о последнем примере, который из жизни.
1. Как вы вычисляете границу?
2. А причём тут метод наименьших квадратов? Тот же принцип, что со стулом на пляже?
1. Как вы вычисляете границу?
2. А причём тут метод наименьших квадратов? Тот же принцип, что со стулом на пляже?
0
Границу я вычисляю через graph cut. Наименьшие квадраты для решения уравнения Пуассона, да, принцип тот же, что и со стулом: я фиксирую границу текстуры быть равной по краям, чтобы она нормально склеилась, а центр текстуры заливается, стараясь быть как можно ближе к вариации исходной текстуры.
+1
Да, я не знаю, зачем нужны в жизни квадратные уравнения.
Вот, кстати, да — тоже мучаюсь этим вопросом со школы. А в целом — большое спасибо за статью. Нужно вообще направление такое в психотерапии организовать — снятие математических комплексов :).
0
— Здравствуйте, меня зовут %username%, и втайне раскрываю суммы из сигма-нотации на листочке, чтобы понять, что там происходит.
— Привет, %username%!
+8
Прочитав "сигма-нотация", почувствовал себя дебилом и полез в интернет, чтобы узнать, что это такое. Оказалось — это значок суммы...
+5
На вскидку:
Строй. механика — эпюры моментов.
Строй. физика — акустика
Строй. механика — эпюры моментов.
Строй. физика — акустика
0
Не подскажете, где об этом можно почитать — в более-менее популярной форме (а-ля библиотечка "квант"), чтобы вот прям с дискриминантами.
0
В инженерных науках не вопрос, я могу найти применение. А вот для чего оно широким слоям населения — ума не приложу. Ни одного применения нет.
0
А как же иначе колебательные процессы в физике изучать? Там же характеристическое уравнение квадратное!
Тут, конечно, меня спросят зачем широким слоям населения колебательные процессы...
Тут, конечно, меня спросят зачем широким слоям населения колебательные процессы...
0
0
Ещё раз, я не оспариваю ни разу полезность умения решать квадратные уравнения для профессионалов. Я хочу понять, зачем они могут быть нужны обычным людям. Понятно, что тот, кто только сидит на диване и смотрит телек, ему и складывать не надо. Давайте примем разумный уровень активности. Вот я строить дом хочу — вполне жизненная ситуация, где мне нужно уметь решать квадратное уравнение? Я с трудом нашёл одно убедительное применение теореме Пифагора, теперь хотелось бы найти такое же для квадратного уравнения. Один пример. Года два уже ищу, ещё не нашёл.
0
- «Математику уже затем изучать нужно, что она ум в порядок приводит». М. В. Ломоносов
- Как отделить будущих "профессионалов" от обывателя на уровне 10-15 лет?
А потому дают всем одинаковый шанс стать профессионалом.
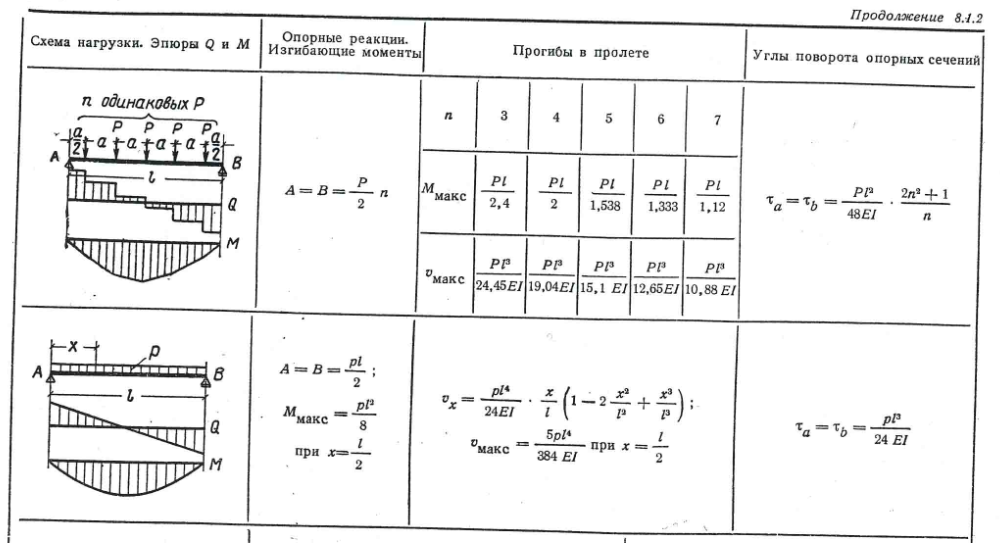
А по поводу Вашей жизненной ситуации со строительством дома, то я уже приводил выше необходимость проверять прочность и прогибы строительных конструкций, в том числе и обратные проверки, при заданных параметрах материалов и заданной нагрузке надо найти пролеты которыми этим материалом можно перекрыть.
+1
Не пойдёт. В реальной жизни, люди, которые хотят построить дом, и выбирают балку, просто смотрят на справочную таблицу, сколько эта конкретная балка выдерживает на такой-то пролёт. Ещё раз, я не про строителя мостов, у которого четверть жизни уйдёт на строительство одного моста, я про реальных людей в реальной жизни, не про инженеров за работой.
0
Уважаемый haqreu, я отвечал не Вам, я отвечал на вопрос, зачем в жизни нужны квадратные уравнения (ссылка). Был дан пример повседневного использования этих уравнений. Зачем Вы пытаетесь ввести дополнительные условия для меня загадка.
А если говорить про реальную жизнь, то люди которые хотят построить дом, делают проект этого дома и в проекте, в том числе, считают балки, перекрытия, стены, стропила, фундаменты. Кстати, эпюра напряжений в земле под подошвой фундамента, опять таки, представляет из себя кривую второго порядка.
В любом случае, отсутствие необходимости в решение кв. уравнений у Вас и в Вашем окружении всего навсего характеризует Вас и Ваше окружение и не является истиной или «статической достоверностью».
За сим, позвольте откланяться, дальнейшее обсуждение лишено смысла.
В реальной жизни, люди, которые хотят построить дом, и выбирают балку, просто смотрят на справочную таблицу, сколько эта конкретная балка выдерживает на такой-то пролёт.— Вы меня извините, но это мнение человека слабо знакомого со строительством. Поясню, такие таблицы есть только для сборных, серийных элементов (С оговоркой, что там так же нужно все перепроверять т.к. условия работы различны), а как быть при монолитном ЖБ или при строительстве жилого деревянного дома? Таблиц на монолитный ЖБ и деревянные конструкции не существует.
А если говорить про реальную жизнь, то люди которые хотят построить дом, делают проект этого дома и в проекте, в том числе, считают балки, перекрытия, стены, стропила, фундаменты. Кстати, эпюра напряжений в земле под подошвой фундамента, опять таки, представляет из себя кривую второго порядка.
В любом случае, отсутствие необходимости в решение кв. уравнений у Вас и в Вашем окружении всего навсего характеризует Вас и Ваше окружение и не является истиной или «статической достоверностью».
За сим, позвольте откланяться, дальнейшее обсуждение лишено смысла.
0
Ну что вы мне рассказываете. Ну вот делал я стропила для черепичной крыши. Пошёл в руководство для дачного строителя и посмотрел, какую нагрузку в килограммах можно ставить на четырёхметровый пролёт сосновой балки такого-то сечения, прикинул вес черепицы и прочее, и выбрал сечение балки. Какие там квадратные уравнения. Ещё раз, я не ввожу никаких новых условий, я просто прошу привести пример не из профессиональной жизни строителя высоток, а просто из жизни человека, который спокойно себе ковыряется на дачном участке / в гараже. Решать уравнения приходится, когда вы хотите, чтобы дом не рухнул, но при этом не нужно потратить ни одной лишней копейки, так как домов вы возводите три десятка. Иначе достаточно оценки снизу, взятой из справочника.
+1
Ну тогда «простым людям» вообще математика за пределами простой арифметики не нужна. Даже отрицательные числа и линейные уравнения избыточны.
0
Не согласен. Отрицательную температура за бортом я вижу часто, долги тоже бывают. И уж пропорцию составить даже на кухне нужно регулярно, зачем вы передёргиваете?
0
Отрицательную температура за бортом я вижу часто, долги тоже бывают.
Не «минус пять градусов», а «пять градусов холода». И нет никаких отрицательных чисел. С долгами ещё проще. Мало кто говорит, что у него есть «минус сто рублей».
Пропорции, кстати, я допускаю. Правило из (какого там класса?) средней школы: рисуем квадратиком, перемножаем по диагонали и делим на оставшееся известное.
А линейные уравнения простому человеку зачем?
зачем вы передёргиваете?
Чтобы продемонстрировать некорректность вашего утверждения о нужности квадратных уравнений в жизни простого человека. Вы не определили, кто такой простой человек и что такое нужно. :)
+2
Я так чувствую, что вы мне ещё скажете, что умножать не умеете, а делаете магические упражнения, записывая числа в столбик. Пропорция — это линейное уравнение, решать его можете каким угодно способом :)
Про минус сто рублей я вас уверяю, банки говорят регулярно. И я вам уже дал ссылки на определения.
Про минус сто рублей я вас уверяю, банки говорят регулярно. И я вам уже дал ссылки на определения.
0
Я так чувствую, что вы мне ещё скажете, что умножать не умеете, а делаете магические упражнения, записывая числа в столбик.
Не в столбик, а квадратиком, как учительница учила. :) А дальше калькулятором. Мы люди простые. Дача, там… Гараж… :)
Пропорция — это линейное уравнение, решать его можете каким угодно способом :)
Пропорция — это частный случай. Вы там внизу что-то подобное писали про коэффициент b в квадратном уравнении. Или поиск стороны квадрата по площади я могу как пример квадратного уравнения привести?
Про минус сто рублей я вас уверяю, банки говорят регулярно. И я вам уже дал ссылки на определения.
Ну так мы ж про простых людей. Чёрточка перед числом — значит должен. Какие-такие отрицательные числа?
Вы, конечно, возразите мне, что это отрицательные, но неявно. А я вам возражу, что когда мы смотрим на спидометр, мы неявно находим производную. А вы мне возразите… Впрочем, не буду лишать вас удовольствия. :)
0
На самом деле не, я уже утомился тут писать. Порезвились — и буде.
0
Кстати, а ведь пропорция — это честное линейное уравнение, это я ночью спать хотел, поверил вам:
ax + b = 0
В рецепте b картошки для оливье на восемь человек, у меня гостей втрое больше, сколько картошки брать? Чистая пропорция, чистое линейное уравнение...
ax + b = 0
В рецепте b картошки для оливье на восемь человек, у меня гостей втрое больше, сколько картошки брать? Чистая пропорция, чистое линейное уравнение...
0
НЛО прилетело и опубликовало эту надпись здесь
Есть нажитые непосильным трудом 4 метра сетки для забора. Надо огородить с трёх сторон прямоугольный кусок земли, прилегающий к стене дома, чтобы сделать там грядку для гладиолусов. Без забора мелкий рогатый скот быстро схарчит все гладиолусы.
Каковы должны быть размеры грядки, чтобы площадь получилась максимальной?
Каковы должны быть размеры грядки, чтобы площадь получилась максимальной?
0
Это известная задача, причём откуда там взялось ограничение на то, что кусок земли должен быть прямоугольным, неясно. Правильный ответ: полукруг максимизирует площадь.
-3
Ограничение на то, что кусок земли должен быть прямоугольным, взялось от заказчика. Полукруг потребует много стоек, которые будут поддерживать сетку.
+1
Скажу по секрету, прямоугольник тоже. И ничуть не меньше. Блин, ну вот что стоит привести один-единственный пример, не притянутый за уши? :)
0
Прямоугольнику нужно только две стойки, по углам.
А смысл? Про любой пример можно сказать, что он притянут за уши, что в жизни таких задач не бывает, что можно решить по-другому и вообще зачем знать про дискриминант, когда есть Wolfram Alpha и Solver в Excel.
Вот почти такой же пример — есть лист формата А4. Надо из него вырезать четыре квадратика по углам и загнуть стороны вверх, чтобы получилась прямоугольная коробка без крышки. При какой высоте коробки получим максимальный объём?
что стоит привести один-единственный пример, не притянутый за уши?
А смысл? Про любой пример можно сказать, что он притянут за уши, что в жизни таких задач не бывает, что можно решить по-другому и вообще зачем знать про дискриминант, когда есть Wolfram Alpha и Solver в Excel.
Вот почти такой же пример — есть лист формата А4. Надо из него вырезать четыре квадратика по углам и загнуть стороны вверх, чтобы получилась прямоугольная коробка без крышки. При какой высоте коробки получим максимальный объём?
+2
Похоже, что тут без производной и квадратного уравнения не обойтись. Хотя можно просто построить табличку в Excel, это будет даже быстрее. И точнее: в решении квадратного уравнения проще допустить ошибку.
0
Табличка в экселе — это просто численный метод решения. Аналитически-численно — это тема для совсем другого разговора, мне просто нужны задачи из жизни. Вот про коробку красивая задача, интересно, можно ли таких набрать достаточно на школьный учебник алгебры, чтобы выкинуть те тексты, что там есть...
0
Дело в том, что табличка маскирует само наличие квадратного уравнения: выписывается не производная, а сам объём (и глазом ищется максимум). Квадратное уравнение возникает только при аналитическом решении.
0
Для школьного учебника алгебры не годится, потому что на момент изучения квадратных уравнений понятие производной ещё не введено. Именно поэтому я сначала предлагал более простой вариант той же задачи на плоскости (с грядкой у стенки), которая решается без производных.
А потом конечно можно, и есть тому хорошие примеры: Sanjoy Mahajan: Street-Fighting Mathematics, Ivan Savov: No BS Guide to Math and Physics.
Книжка по физике от Sanjoy Mahajan ещё круче, одно вычисление тротилового эквивалента по трём кадрам рассекреченного фильма чего стоит.
А потом конечно можно, и есть тому хорошие примеры: Sanjoy Mahajan: Street-Fighting Mathematics, Ivan Savov: No BS Guide to Math and Physics.
Книжка по физике от Sanjoy Mahajan ещё круче, одно вычисление тротилового эквивалента по трём кадрам рассекреченного фильма чего стоит.
0
вычисление тротилового эквивалента по трём кадрам рассекреченного фильма чего стоит
Интересно. А можно подробнее?
0
"Тут на полях мало места, чтобы объяснить это замечательное доказательство."
Там надо сначала метод анализа размерности ввести. Из него получается, что произведение энергии взрыва на время в квадрате примерно равно произведению плотности воздуха на радиус ударной волны в пятой степени. Радиус ударной волны видно на кадрах фильма, время тоже, плотность воздуха знаем. МНК тоже используется, кстати.
В книжке (доступной безвоздмездно, то есть даром) страница 150, глава 5.2.2.
Там надо сначала метод анализа размерности ввести. Из него получается, что произведение энергии взрыва на время в квадрате примерно равно произведению плотности воздуха на радиус ударной волны в пятой степени. Радиус ударной волны видно на кадрах фильма, время тоже, плотность воздуха знаем. МНК тоже используется, кстати.
В книжке (доступной безвоздмездно, то есть даром) страница 150, глава 5.2.2.
0
во-первых, тут можно и без полного определения производных обойтись; а потом, почему производные должны быть введены после квадратных уравнений, а не до?
0
Потому что производные (с полным определением или без) предполагают какое-никакое умение работать с функциями. У изучающих алгебру школьников такого умения ещё нет. Оно в частности нарабатывается рисованием парабол.
"Где парабола пересекает ось x" понять проще, чем "предел отношения приращения функции к приращению аргумента при последнем, стремящемся к нулю" или "коэффициент первого элемента в ряду Тейлора".
"Где парабола пересекает ось x" понять проще, чем "предел отношения приращения функции к приращению аргумента при последнем, стремящемся к нулю" или "коэффициент первого элемента в ряду Тейлора".
0
Безусловно, а можно и шарики катать по столу и рисовать графики. Не уверен я, что это так необходимо — изучать квадратные уравнения в восьмом (не помню точно) классе, а не в десятом.
0
Без квадратных уравнений как минимум в самом начале 9 класса, нереально изучать кинематику на физике, квадратные уравнения так же появляются в 9 классе в задачах по геометрии.
Надо или согласованно всё двигать(но зачем?) или признать, что квадратные уравнения изучать нужно не позже начала 9 класса.
В рамках школьной( да и в институте тоже) физики всё время приходится рассказывать мат. аппарат самому, только потому что он используется, а его еще не объясняли. Зачем усугублять то? Ну или просто не учить физику. Оставить нормальную математику и физику только в физмат классе, есть и такой вариант.
Надо или согласованно всё двигать(но зачем?) или признать, что квадратные уравнения изучать нужно не позже начала 9 класса.
В рамках школьной( да и в институте тоже) физики всё время приходится рассказывать мат. аппарат самому, только потому что он используется, а его еще не объясняли. Зачем усугублять то? Ну или просто не учить физику. Оставить нормальную математику и физику только в физмат классе, есть и такой вариант.
0
Вы забор когда-нибудь ставили? Это к вопросу о двух стойках по углам...
-2
Два метра сетки между двумя столбами натягивал. Если столбы хорошо вкопать, а поверху натянуть трос, то держится.
+1
Дык, четыре метра сетки — это не тот объём, где реально можно захотеть максимизировать площадь. На четырёхстах я ещё пойму. Кроме того, угловые столбы всегда дороже, т.к. на них приходится большая нагрузка, или их дополнительно нужно якорить тросами наружу...
В общем, эту задачу я считаю существенно менее элегантной, нежели про коробку.
В общем, эту задачу я считаю существенно менее элегантной, нежели про коробку.
0
Кстати, а вы знаете, задача про объём коробки мне нравится, я вполне могу представить себе подобную ситуацию. Большое спасибо! Действительно, ограничение на площадь листа материала вполне правдоподобно, ну вот только такого размера у меня есть листы жести, и нужно мне хранить что-нибудь сыпучее. Да, правдоподобно! Пишу жирно, чтобы ваш текст был виден в этой простыне комментариев.
0
Посоветоваться с женой. Она объяснит, какая грядка лучше всего вписывается в её идею прекрасного, а какая там будет площадь — дело десятое.
Отразим грядку относительно стены дома, объединим грядку с её отражением. Получится прямоугольная грядка вдвое большей площади, которую надо оградить уже со всех сторон, но на это есть вдвое больше метров сетки. Прямоугольник максимальной площади при заданном периметре — квадрат. Значит, искомая грядка — 1х2 метра. Где здесь квадратное уравнение? (почему квадрат — а потому, что среднее арифметическое не меньше среднего геометрического).
Аналогично получаем, что если форма может быть произвольной, то ответ — полукруг.
Отразим грядку относительно стены дома, объединим грядку с её отражением. Получится прямоугольная грядка вдвое большей площади, которую надо оградить уже со всех сторон, но на это есть вдвое больше метров сетки. Прямоугольник максимальной площади при заданном периметре — квадрат. Значит, искомая грядка — 1х2 метра. Где здесь квадратное уравнение? (почему квадрат — а потому, что среднее арифметическое не меньше среднего геометрического).
Аналогично получаем, что если форма может быть произвольной, то ответ — полукруг.
+3
Осталось узнать, почему прямоугольник максимальной площади — квадрат.
0
Потому, что среднее арифметическое не меньше среднего геометрического. Очевидно же!
+2
Я видел, можно вообще посчитать три-четыре варианта наугад и выбрать наилучший, или сделать на глазок — на практике разницы не будет заметно.
Вообще вряд ли есть задача, которую можно решить исключительно использованием квадратного уравнения. При этом есть много прикладных задач, где надо находить максимум или минимум, что для параболы легко, если знать школьную программу. А параболы встречаются сплошь и рядом.
Вообще вряд ли есть задача, которую можно решить исключительно использованием квадратного уравнения. При этом есть много прикладных задач, где надо находить максимум или минимум, что для параболы легко, если знать школьную программу. А параболы встречаются сплошь и рядом.
0
А вот тут вы ошибаетесь! Мы говорим про квадратное уравнение, а это есть пересечение параболы и прямой, а вовсе не минимум параболы. Минимум квадратичной функции легко находится, а мы говорим про нахождение экстремумов кубической функции.
0
Нет тут кубической функции. Максимизируем площадь, она измеряется в квадратных метрах, поэтому функция квадратная.
Надо найти максимум параболы x(4-2x), где x — это длина стороны грядки, прилегающей к дому. Максимум там, где горизонтальная прямая касается параболы.
Берём формулу корней квадратного уравнения, подставляем в неё нулевой дискриминант, получаем искомый результат x = -b/2a = 1. Или усредняем два корня (x=0 и x=2), вспомнив, что квадратная парабола симметрична.
Разумеется, можно найти максимум ещё проще, если знать, что такое производная. Но для этого надо знать, что такое производная.
Надо найти максимум параболы x(4-2x), где x — это длина стороны грядки, прилегающей к дому. Максимум там, где горизонтальная прямая касается параболы.
Берём формулу корней квадратного уравнения, подставляем в неё нулевой дискриминант, получаем искомый результат x = -b/2a = 1. Или усредняем два корня (x=0 и x=2), вспомнив, что квадратная парабола симметрична.
Разумеется, можно найти максимум ещё проще, если знать, что такое производная. Но для этого надо знать, что такое производная.
-2
Как-то вы быстро к нулевому дискриминанту перешли… Особенно учитывая что для многочлена -2x2 + 4x он ненулевой.
То, о чем вы говорите, называется "формула вершины параболы". Она записывается как x0 = -b/2a без всяких дискриминантов и к квадратным уравнениям не имеет никакого отношения.
То, о чем вы говорите, называется "формула вершины параболы". Она записывается как x0 = -b/2a без всяких дискриминантов и к квадратным уравнениям не имеет никакого отношения.
0
Разумеется ненулевой, потому что два корня. А нас интересует тот случай, когда он нулевой, то есть когда оба корня совпадают.
Если в формулу квадратного уравнения x1,2=(-b+-sqrt(D))/2a подставить D=0, получаем ту самую "формулу вершины параболы". И это не просто совпадение.
Если в формулу квадратного уравнения x1,2=(-b+-sqrt(D))/2a подставить D=0, получаем ту самую "формулу вершины параболы". И это не просто совпадение.
0
Искать минимум параболы — это линейная задача. Квадратичное уравнение — это экстремумы кубической функции или геометрическое пересечение окружности и прямой, чего в вашем примере нет.
0
Я привёл пример самой простой задачи, в которой есть квадратная функция и которая решается в лоб использованием формулы для корней квадратного уравнения в качестве контрпримера к следующему высказыванию:
я не знаю, зачем нужны в жизни квадратные уравнения
0
a^2 > (a+dx)*(a-dx)
+1
Уравнение прямой на плоскости, строго говоря, выглядит так:
то, что вы привели, не описывает прямые, параллельные оси ординат (x = c)
Не знаю, что такое "стандартный", но настоящий математик заметит, что если система совместная (теорема Кронекера-Капелли в помощь), то третье уравнение выводится из двух остальных.
Программист, опять же настоящий, вначале потребует точной постановки задачи, а потом уже будет затейливо проводить прямую.
ax + by = c то, что вы привели, не описывает прямые, параллельные оси ординат (x = c)
Стандартный математик скажет, что решения не существует. А что скажет программист?
Не знаю, что такое "стандартный", но настоящий математик заметит, что если система совместная (теорема Кронекера-Капелли в помощь), то третье уравнение выводится из двух остальных.
Программист, опять же настоящий, вначале потребует точной постановки задачи, а потом уже будет затейливо проводить прямую.
+3
Спасибо, но я достаточно видел математиков, писали код, отказывающийся строить триангуляцию Делоне для коциклических точек. Типа, не существует, валимся с ошибкой. А что дальше с ошибкой этой делать — конечному пользователю софта неясно. Поэтому ваш коммент мимо.
0
Вывод — математиками те люди были только на словах.
Раз уж вы начали оперировать мат.аппаратом, так делайте это корректно. Иначе в чём смысл всего поста? Сообщить, что бывают недобросовестные преподаватели мат.дисциплин? Да, бывают.
Раз уж вы начали оперировать мат.аппаратом, так делайте это корректно. Иначе в чём смысл всего поста? Сообщить, что бывают недобросовестные преподаватели мат.дисциплин? Да, бывают.
+3
Подскажите, пожалуйста, где мой матаппарат был некорректен, я с радостью исправлю.
+2
См. мой первый комментарий. Там как бы всё указано. Уравнение прямой на плоскости в общем виде вы привели неверно (не включает прямые, параллельные оси ординат).
0
Это очевидно и сделано в угоду тому, что мне нужно было только две переменные, а то четырёхмерных рисунков я делать пока не научился.
0
OK, т.е. цель поста — малость поглумиться над математикой. Тогда вопросов больше нет.
+1
Извините, не троллю, но реально пытался понять — зачем четырёхмерные рисунки для уравнений ax + by = c?
+1
Размерность вектора ошибки (e) равна количеству уравнений в системе. При трёх неизвестных минимальное количество уравнений нетривиальной системы равно четырём.
Вот такую картинку уже не нарисовать, а она является одной из ключевых для понимания происходящего:
Вот такую картинку уже не нарисовать, а она является одной из ключевых для понимания происходящего:
Скрытый текст

0
Подождите… а где три неизвестных?
ax + by = c — тоже два неизвестных, а третье выводится из ограничения.
ax + by = c — тоже два неизвестных, а третье выводится из ограничения.
0
Не забывайте, что точного решения этой системы в общем случае не существует (четыре уравнения, три неизвестных), поэтому нельзя просто взять и вывести третье из первых двух.
0
Да не, не надо уравнения выводить.
В этой задаче вы же хотите найти зависимость.
Так как три неизвестных, то фиксируется два из них, а третье ищется.
Вернее, ищется закон.
При совместной системе точный, при несовместной приближённый.
Чем больше уравнений (при независимости наблюдений), тем точнее приближение.
Опять же при адекватности модели.
В этой задаче вы же хотите найти зависимость.
Так как три неизвестных, то фиксируется два из них, а третье ищется.
Вернее, ищется закон.
При совместной системе точный, при несовместной приближённый.
Чем больше уравнений (при независимости наблюдений), тем точнее приближение.
Опять же при адекватности модели.
0
Я не понимаю, о чём вы говорите. Можете привести полный способ решения? Ищем ax+by+c=0; имеется четыре точки данных. Дальше что?
0
Так же, три точки данных.
ax+by+c=0 — это другой вид написания уравнения y = ax + b
С точностью до коэффициентов и ограничения на решение вида x = c.
Потому что мы подразумеваем, что y — функция однозначная.
Можно выразить через
x = ey + f
ax+by+c=0 — это другой вид написания уравнения y = ax + b
С точностью до коэффициентов и ограничения на решение вида x = c.
Потому что мы подразумеваем, что y — функция однозначная.
Можно выразить через
x = ey + f
0
Только на ноль делить нельзя, вы упёрлись ровно в ту же проблему, с которой начали.
0
Вот спинным мозгом чувствую, но выразить не могу.
По идее классическая постановка МНК выглядит как
a11x1 + a12x2 +… + a1nxn = b1
…
am1x1 + am2x2 +… + amnxn = bm
и решение ищется как x=A+b,
где A+ — псевдообратная матрица к A.
Тут n неизвестных и m уравнений.
В Вашей постановке x — это x1, а y — это x2.
Два неизвестных — три уравнения.
Хотя возможно я уже просто запутался с обозначениями.
По идее классическая постановка МНК выглядит как
a11x1 + a12x2 +… + a1nxn = b1
…
am1x1 + am2x2 +… + amnxn = bm
и решение ищется как x=A+b,
где A+ — псевдообратная матрица к A.
Тут n неизвестных и m уравнений.
В Вашей постановке x — это x1, а y — это x2.
Два неизвестных — три уравнения.
Хотя возможно я уже просто запутался с обозначениями.
0
Нет, даже ещё проще.
x — это x1, а y — это b.
Да, похоже, что Вы правы.
Но для меня было просто как-то непонятно почему МНК не может дать ответ в случае x = c.
x — это x1, а y — это b.
Да, похоже, что Вы правы.
Но для меня было просто как-то непонятно почему МНК не может дать ответ в случае x = c.
0
Без проблем может, но только рисунок получиется четырёхмерным :)
0
Проблема в том, как мы вычисляем штраф за взаимное расположение точки (x0,y0) и прямой. Если прямая задана как a x + b y = c, а штраф — (a x0 + b y0 — c)/sqrt(a^2+b^2), т.е. расстояние до прямой — картина одна. Если прямая y = a x + c, а штраф — a x0 + c — y0, то результат будет другим — повысится штраф в случае больших значений a, и метод будет занижать это значение по сравнению с первым представлением. И при переходе от y = a x + c к x=c будет разрыв непрерывности.
Какой ответ для точек (-1,6), (0,0), (1,6)? y=4 или x=0?
Какой ответ для точек (-1,6), (0,0), (1,6)? y=4 или x=0?
0
А откуда взялся делитель sqrt(a^2+b^2)?
Штрафы, как мне кажется, тут идентичные, с точностью до нормирующих коэффициентов, и разницы между случаями для полученной формулы прямой не будет.
Что касается разрыва непрерывности, то он появляется в результате требования однозначности отображения.
То есть, для функции y(x) запрещено принимать несколько значений, иначе смысл в минимизации отклика отсутствует, раз отклик может принимать множество значений (а в случае x = c бесконечное неограниченное в обе стороны множество).
Штрафы, как мне кажется, тут идентичные, с точностью до нормирующих коэффициентов, и разницы между случаями для полученной формулы прямой не будет.
Что касается разрыва непрерывности, то он появляется в результате требования однозначности отображения.
То есть, для функции y(x) запрещено принимать несколько значений, иначе смысл в минимизации отклика отсутствует, раз отклик может принимать множество значений (а в случае x = c бесконечное неограниченное в обе стороны множество).
0
А откуда взялся делитель sqrt(a^2+b^2)?
Если мы будем минимизировать сумму (ax+by-c)^2, то алгоритм выдаст a=b=c=0, и ничего с ним не сделать.
Если взять точки (-2,0), (0,0), (3,0), то оптимальная прямая при штрафе (ax+by-c)/sqrt(a^2+b^2) будет y=x+4/3, а при штрафе ax+c-y — y=(6x+9)/7. Разница невелика, но она есть.
+1
дорисовал_сову.jpg
> «Давайте заменим конкретные матрицы на их символьное представлени… бла-бла-бла… Окей, тут всё понятно»
Вы сами только что написали что нихрена не понятно даже простые определения. Что очень много вещей нужно по настоящему разжевывать. и тут вдруг над буквой появляется непонятная стрелочка, у матриц появляются степени и вообще непонятно как и каким образом одно следует из другого… Но «Окей, тут всё понятно».
> «Давайте заменим конкретные матрицы на их символьное представлени… бла-бла-бла… Окей, тут всё понятно»
Вы сами только что написали что нихрена не понятно даже простые определения. Что очень много вещей нужно по настоящему разжевывать. и тут вдруг над буквой появляется непонятная стрелочка, у матриц появляются степени и вообще непонятно как и каким образом одно следует из другого… Но «Окей, тут всё понятно».
+28
Текст рассчитан на конкретно моих студентов с конкретно их бэкграундом. Что такое матрица — они знают. И стрелочка для обозначения вектора им знакома. А вот "задача Дирихле" им совсем неясна, хотя считать там чаще всего нечего совсем. Пересказать весь школьный курс я себе задачи не ставил.
-8
Думаю что надо было об этом намекнуть в начале статьи. Всё таки хабр — публичный ресурс и статьи для узкого/определённого круга лиц — всё равно что рецепт по выпечке на форуме радиолюбителей.
Думаю обычного упоминания того что вы в являетесь преподавателем на конкретном курсе в высшем учебном заведении было бы достаточно. Хоть это и может выглядеть как хвастовство, зато сразу морально готовишь себя к тому что вы называете «на пальцах».
Думаю обычного упоминания того что вы в являетесь преподавателем на конкретном курсе в высшем учебном заведении было бы достаточно. Хоть это и может выглядеть как хвастовство, зато сразу морально готовишь себя к тому что вы называете «на пальцах».
+7
Никто не говорит про запретить.
Замечание про сову совершенно справедливое, попробуйте воспринимать критику более конструктивно.
Переводить стрелки и сравнивать энциклопедию и блоговый сервис — не очень корректно, на мой взгляд.
Замечание про сову совершенно справедливое, попробуйте воспринимать критику более конструктивно.
Переводить стрелки и сравнивать энциклопедию и блоговый сервис — не очень корректно, на мой взгляд.
+1
Ну раз так, то его и публиковать надо для ваших студентов на вашестудентском ресурсе.
+1
Все гении такие. Пишут как-то Ландау и Лифшиц "Электродинамику сплошных сред", ну и в одной главе получают какую-то сумасшедшую формулу с использованием максвелловского тензора напряжений в анизотропной среде. А на след. день Лифшиц говорит: "Слушай, я вчера три листа выкладок в трамвае потерял. Что делать?" "А что, — говорит Ландау, — напишем, как обычно: "откуда очевидно..."
+14
Вспоминается одна реальная история про какого-то из известных математиков, (не помню какого). Преподавал он лекцию студентам, и на очередной фразе "… откуда очевидно, что..." запнулся, остановился, завис, потом схватил бумагу, начал что-то строчить, потом весь возбуждённый что-то бормоча выскочил за дверь и отсутствовал минут двадцать. После чего вернулся с сияющим видом, и как ни в чём не бывало, продолжил: "действительно, совершенно очевидно, что...".
+7
Я ее слышал про Харди, кажется)
+1
Хм, интересно.
А нам преподаватель по матану подобную историю рассказывал про своего преподавателя. Типа студент на экзамене забыл часть доказательства и сказал "отсюда очевидно". Преподаватель ходил где-то 20 минут, думал, вернулся и сказал "действительно очевидно".
Значит байка:(
А нам преподаватель по матану подобную историю рассказывал про своего преподавателя. Типа студент на экзамене забыл часть доказательства и сказал "отсюда очевидно". Преподаватель ходил где-то 20 минут, думал, вернулся и сказал "действительно очевидно".
Значит байка:(
0
Соотношение первой и второй частей статьи очень напомнило "как нарисовать сову".
+27
Задачи показать конкретный софт не стояло; задача стояла показать, что такое наименьшие квадраты. Конечные картинки так, тизер. А решать мои студенты будут вообще задачу оптимального управления роботами, а не картинки рисовать.
0
Я не про софт. :) Первая часть — всё просто, известно и пережёвано. И потом бах и уравнения с граничными условиями, где вообще не ясно, что происходит и причём тут МНК.
0
Хм. Видно, плохо объяснил. Уравнения с граничными условями ничем не отличаются от самой первой микрозадачи. У нас есть некий набор линейных уравнений, например, для сглаживания поверхности:
1) (для всех пар соседних вершин) соседние вершины должны быть равны
2) (для всех вершин) отклонение вершины от изначальной позиции должно быть нулевым
Очевидно, что точно выполнить все условия никак, поэтому делается некий компромисс между всем и ищется решение, минимизирующее квадрат ошибки. Ровно как для самой первой задачи.
1) (для всех пар соседних вершин) соседние вершины должны быть равны
2) (для всех вершин) отклонение вершины от изначальной позиции должно быть нулевым
Очевидно, что точно выполнить все условия никак, поэтому делается некий компромисс между всем и ищется решение, минимизирующее квадрат ошибки. Ровно как для самой первой задачи.
0
НЛО прилетело и опубликовало эту надпись здесь
К сожалению, не могу сказать, никогда не залезал в классификацию.
0
Более гладко не получится. У алгоритма появятся лишние степени свободы, он сможет более точно аппроксимировать исходные точки, а значит, найденное решение будет ближе к исходным данным. И, скорее всего, будет менее гладким.
Впрочем, в МНК легко засунуть и полиномиальные сплайны, и условия гладких (или более-менее гладких) стыковок, и разный вес разных условий.
Впрочем, в МНК легко засунуть и полиномиальные сплайны, и условия гладких (или более-менее гладких) стыковок, и разный вес разных условий.
0
Теорию алгоритмов они тоже на пальцах изучают? Или таки по-настоящему?
Кстати, было бы интересно посмотреть на объяснение "на пальцах" гиперреальных чисел и, скажем, доказательства Уайлса Великой Теоремы Ферма — в вашем исполнении. Ну или поручите студентам во всём этом разобраться.
Кстати, было бы интересно посмотреть на объяснение "на пальцах" гиперреальных чисел и, скажем, доказательства Уайлса Великой Теоремы Ферма — в вашем исполнении. Ну или поручите студентам во всём этом разобраться.
0
Гиперреальные числа только на пальцах и можно объяснить — они очень близко к базовым понятиям. Система подмножеств, фильтры с примерами, главные и неглавные ультрафильтры — и всё. Проблема — понять зачем они нужны. Я так и не понял их преимущества над полем каких-нибудь хитрых обобщённых степенных рядов. Там и упорядоченность есть, и нужная мощность, и бесконечно малые на любой вкус. И построение гораздо более конструктивно.
0
Статья неплохая, но наезды на математиков безосновательны. Так как статья, в общем, делает то же самое, что и они.
Вначале — забавные байки про то, что никто не знает что такое производная, а потом… трац-бах матричный вид, вектора, что-то там куда-то натянуто, какие-то ортогонали. Вы уверены, что потенциальный читатель вашей статьи точно про всё это знает?
Собственно это проблема обучения вообще: нужно что-то знать про того, кому ты пытаешься что-то рассказать. Иначе любая простенькая теория превратится в талмуд на 10000 страниц. В это и вся проблема "рассказа на пальцах": то, что у одного человека "на пальцах" у другого не помещается в голове никак вообще. Какие-нибудь простейшие геометрические построения (или, наоборот, линейна алгебра) — и человек "умирает"...
Вначале — забавные байки про то, что никто не знает что такое производная, а потом… трац-бах матричный вид, вектора, что-то там куда-то натянуто, какие-то ортогонали. Вы уверены, что потенциальный читатель вашей статьи точно про всё это знает?
Собственно это проблема обучения вообще: нужно что-то знать про того, кому ты пытаешься что-то рассказать. Иначе любая простенькая теория превратится в талмуд на 10000 страниц. В это и вся проблема "рассказа на пальцах": то, что у одного человека "на пальцах" у другого не помещается в голове никак вообще. Какие-нибудь простейшие геометрические построения (или, наоборот, линейна алгебра) — и человек "умирает"...
+20
НЛО прилетело и опубликовало эту надпись здесь
Я учу не абстрактного коня в вакууме, а своих студентов. И что такое два перпендикулярных вектора — они знают. Абстрактному читателю текст написать невозможно. Один уснёт от скуки, потому что слишком просто, а второй от скуки, потому что сложно. Ну вот вам скучно по одной из этих причин, что ж поделать.
-6
Но стоит ли публиковать на Хабре статью, "заточенную" строго под ваших студентов — вот в чём вопрос.
+9
Безусловно, задаваться вопросом о полезности действий надо. Поделитесь вашим мнением по этому поводу.
+3
Думаю, критика связана с тем, что по ходу изложения пропущены некоторые важные шаги, отсутствие которых прерывает осознание материала на пути от простого к сложному, и перед читателем возникает тот самый классический пример рисования совы.
Что до (ваших) студентов, как целевой аудитории, если они понимают заключительную (сложную) часть, наверное нет смысла им все так досконально разжёвывать с самого начала, но если уж разжёвывать перед широким кругом читателей, то шажки нужны помельче.
Что до (ваших) студентов, как целевой аудитории, если они понимают заключительную (сложную) часть, наверное нет смысла им все так досконально разжёвывать с самого начала, но если уж разжёвывать перед широким кругом читателей, то шажки нужны помельче.
+7
По причине некоторых запретов в правилах Хабра я не могу воспользоваться всеми словами русского языка, чтобы сказать, насколько хорошая статья получилась, и насколько правильное дело вы делаете; поэтому просто знайте, что статья получилась очень хорошая, и дело вы делаете очень правильное.
+6
Как только вы пытаетесь прочитать какой-то текст, и вам кажется, что он чрезмерно сложен, то знайте, что он хреново написан. Я утверждаю, что нет ни одной области математики, о которой нельзя говорить «на пальцах», не теряя при этом точности.
Яснопонятно.
P.S. Не то что бы в формулах что-то запредельное, но и объяснением "на пальцах" эту статью с трудом можно назвать.
За саму статью спасибо.
+35
del
0
НЛО прилетело и опубликовало эту надпись здесь
Для тех, кто не учился на технических факультетах. Для тех кто учился, но давно. Для тех, кто учился, но ничего не понял. Да много для кого. Иными словами, когда мы говорим "на пальцах", подразумевается — для любого неподготовленного человека. Надо ли это ему — другой вопрос. Я лишь обратил внимание, что такое изложение — это ни разу не "на пальцах".
+18
Задача на ближайшее время: я поручил своим студентам понять, что такое линейно-квадратичный регулятор.Скажите, а студенты уже знакомы с основами ТАУ? Они поймут контекст задачи?
Производная ничто иное, как просто мера того, насколько функция, которую мы дифференцируем, похожа на функцию y=x, y=x^2, y=x^3Ну очень сомнительное для меня утверждение.
-1
1) Нет, студенты с теорией управления не знакомы, но обратный маятник и тому подобное им сделать придётся, для того и пишу текст, чтобы поняли
2) Ну а с сомнительным утверждением можете спорить.
2) Ну а с сомнительным утверждением можете спорить.
+1
1) Это какой-то авторский курс? Просто я не очень понимаю, зачем кому-то знать теоретические основы расчёта ЛКР, не владея основами ТАУ как таковой. Мне кажется, что фрагментированное знание, не вписанное в правильный контекст и, как следствие, не связанное этим контекстом с другими знаниями, плохо усваивается и быстро выветривается. А обособленное знание вывода ЛКР мне кажется именно таким фрагментированным. Но я Ваш курс целиком не видел, так что это только поверхностное впечатление.
Кстати, под обратным маятником Вы имеете ввиду стабилизацию верхнего неустойчивого положения равновесия?
Кстати, под обратным маятником Вы имеете ввиду стабилизацию верхнего неустойчивого положения равновесия?
0
Я вам больше скажу, я сам с теорией управления незнаком. А у студентов есть конкретные задачи, например, да, активная стабилизация в неустойчивом равновесии, типа сигвеев. Ну и я по мере сил даю им направления, куда копать. Так что, теоретических выводов не будет, исключительная практика.
0
А Вы консультировались с кем-то, кто знает ТАУ? Или самостоятельно прорешивали эту задачу? Точнее, даже, а Вы уверены, что тот маршрут, по которому Вы сейчас ведёте студентов, он вообще ведёт туда, куда надо?
Подскажите, что за дисциплину Вы преподаете и какому курсу студентов? Я теряюсь в догадках.
Подскажите, что за дисциплину Вы преподаете и какому курсу студентов? Я теряюсь в догадках.
0
2) Зачем и о чём спорить? Когда кто-то предлагает необычную трактовку устоявшихся понятий, то это от автора трактовки ждешь аргументов и пояснений, а пока их нет, то и спорить не с чем, мало ли кто как пошутил. Про саму же формулировку я уже высказался, на столько вежливо, как только смог. :)
+1
Мне кажется, я ничего нового не выдвигал, всё уже сказал господин Тейлор :)
0
А Тейлор говорил про производную как "меру" похожести? Надо же, не знал. Поясните тогда, чем больше производная, тем что? тем похожее или тем не похожее?
0
Чем ближе к единице, тем похожее. Тейлор показал разложение в функциональном базисе, причём ещё и с убывающей "полезностью" компонент базиса.
0
О, я понял Вашу мысль. Т.е. чем ближе производная к, например, 3, тем более функция похожа на 3x. Мда, своеобразно.
+2
На самом деле, не своеобразно ни разу; достаточно посмотреть на определение, например, дробной производной, тогда подобная интуиция так и просится наружу.
0
Откуда берётся убывающая полезность из этого объяснения совершенно неочевидно. Например, при разложении в ряд Фурье никаких факториалов нет, при разложении на вейвлеты — тоже. Все гармоники одинаково полезны. А у Тейлора факториалы в знаменателе каждого коэффициента.
При обычном объяснении совершенно понятно, откуда они берутся — мы приравниваем i-ю производную многочлена i-й производной нашей функции, в производной многочлена появляется факториал, на который приходится делить.
При обычном объяснении совершенно понятно, откуда они берутся — мы приравниваем i-ю производную многочлена i-й производной нашей функции, в производной многочлена появляется факториал, на который приходится делить.
0
Для меня мир окончательно и бесповоротно изменился не тогда, когда я с третьей попытки сдал "вышку" на тройку на втором курсе, а когда я узнал, что существует решение уравнения cos(x) = -2
После этого даже воспоминания о том, что когда-то я думал, что понимаю математику, растворились в тумане невежества.
После этого даже воспоминания о том, что когда-то я думал, что понимаю математику, растворились в тумане невежества.
+5
Срочно прошу написать чему же равен x в вашем примере.
+3
x примерно равен 6.2832 n — (3.1416-1.3170 i) или 6.2832 n + (3.1416-1.3170 i). https://www.wolframalpha.com/input/?i=cos%5Bx%5D%3D-2
+4
лол… это как на энигме я задавал вопрос: «как из свинца получить золота?» ответ: «добавить золото и убрать свинец».
так и здесь есть какой то подвох…
wolframalpha говорит что x = 2 pi n-cos^(-1)(-2)
независимо от n: получится 2 куска для решений:
2 pi и cos^(-1)(-2)
cos^(-1)(-2) я разбил на cos (-2) = -0.416146…
и на -1 степень от полученного. = -2,402997962…
2pi = 6,283185307…
попробуем решить для простоты в качестве n возьмём 1.
получаем x = 6,2831 — (-2,40299) = 6,2831… + 2,40299… = 8,686183269… обычное такое число и косинус от него -0,739415412…
При выборе другого n ответ получается тот же.
Таким образом предложенный ответ не является решением уравнения.
так и здесь есть какой то подвох…
wolframalpha говорит что x = 2 pi n-cos^(-1)(-2)
независимо от n: получится 2 куска для решений:
2 pi и cos^(-1)(-2)
cos^(-1)(-2) я разбил на cos (-2) = -0.416146…
и на -1 степень от полученного. = -2,402997962…
2pi = 6,283185307…
попробуем решить для простоты в качестве n возьмём 1.
получаем x = 6,2831 — (-2,40299) = 6,2831… + 2,40299… = 8,686183269… обычное такое число и косинус от него -0,739415412…
При выборе другого n ответ получается тот же.
Таким образом предложенный ответ не является решением уравнения.
-5
Таким образом предложенный ответ не является решением уравнения.Ну если от «предложенного ответа» взять примерно так половину, то да, конечно. Как вы из комплексного числа «3.11416… — 1.3170 i» вдруг получили действительное -2,40299 — для меня загадка…
+3
А для меня загадка как из числа лежащего на оси ox в пределах от -1 до 1 (тригонометрическая окружность) вы умудрились вообще предположить что там может быть 2?
да там даже в графике в wolframalpha на рисуемом рисунке красная полоска не пересекается с графиком функции что явно намекает о том что решений нет…
wolframalpha говорит что «3.1416… — 1.3170 i» в другой форме можно представить как cos^(-1)(-2) которые ещё можно записать как 1/cos(2) который в свою очередь wolframalpha уже рассчитывает как -2.40299…
https://www.wolframalpha.com/input/?i=cos^%28-1%29%28-2%29
и вообще i это сколько? этот ваш «3.1416… — 1.3170 i» скорее всего как глюк «20,4*3212,5» в екселе.
да там даже в графике в wolframalpha на рисуемом рисунке красная полоска не пересекается с графиком функции что явно намекает о том что решений нет…
wolframalpha говорит что «3.1416… — 1.3170 i» в другой форме можно представить как cos^(-1)(-2) которые ещё можно записать как 1/cos(2) который в свою очередь wolframalpha уже рассчитывает как -2.40299…
https://www.wolframalpha.com/input/?i=cos^%28-1%29%28-2%29
и вообще i это сколько? этот ваш «3.1416… — 1.3170 i» скорее всего как глюк «20,4*3212,5» в екселе.
-5
Эммм… Дело в том, что под cos^(-1) тут следует понимать не 1/cos, а arccos, тогда не встает ли все на места?)
0
честно говоря вообще не встало… чтобы мы не получали итоговая функция всё равно cosинус который один хрен не может быть меньше -1 и больше 1. По определению там происходит деление катета на гипотенузу. Гипотенуза всегда больше катетов и поэтому мы никаким образом не получим число больше единицы.
0
Тогда вам, вероятно, следует ознакомиться еще лишний раз с тем, что такое косинус.
Есть наивное определение cos — отношения катета к гипотенузе, по сути функция (R+, R+) -> R[-1, 1] (из двух положительных действительных чисел в действительное на отрезке [-1, 1])
Оперировать двумя числами неудобно — поэтому (R+, R+) была заменена на R — угол. итого мы имеем функцию
cos® -> R[-1, 1]
Но ведь согласитесь, где вы видели прямоугольный треугольник с одним из углов равным -1345 градусам? Уже в этот момент мы отошли от наивного определения.
После того, как в математике появились комплексные числа — все стандартные функции были расширены на комплексную плоскость. В том числе и тригонометрические — и оказалось, что cos© уже не попадает в R[-1, 1] и может принимать сколь угодно большие значения — в том числе и -2.
Есть наивное определение cos — отношения катета к гипотенузе, по сути функция (R+, R+) -> R[-1, 1] (из двух положительных действительных чисел в действительное на отрезке [-1, 1])
Оперировать двумя числами неудобно — поэтому (R+, R+) была заменена на R — угол. итого мы имеем функцию
cos® -> R[-1, 1]
Но ведь согласитесь, где вы видели прямоугольный треугольник с одним из углов равным -1345 градусам? Уже в этот момент мы отошли от наивного определения.
После того, как в математике появились комплексные числа — все стандартные функции были расширены на комплексную плоскость. В том числе и тригонометрические — и оказалось, что cos© уже не попадает в R[-1, 1] и может принимать сколь угодно большие значения — в том числе и -2.
+1
а есть картинка?
0
просто читайте соответствующие материалы, там все написано) http://mathworld.wolfram.com/Cosine.html
0
ну пожалуйста… ткните носом куда конкретно смотреть. В английском не бельмеса я.
0
Я конечно сам русский язык знаю на троечку, но авторы учебника по первой ссылки видимо даже собственное предисловие не читали. «Развнтие», «не только, сообщенне известиого», «идейио», «готовнт» и т.д…
Буду держать вас в курсе :)
Буду держать вас в курсе :)
0
Это вы не видели ещё формулу Эйлера, там вообще показатели степени мнимые.
Собственно, эта формула и позволяет расширить тригонометрические функции на комплексную плоскость.
Но лучше всего прослушать лекции по матанализу и теории функции комплексного переменного в каком-нибудь ВУЗе.
Собственно, эта формула и позволяет расширить тригонометрические функции на комплексную плоскость.
Но лучше всего прослушать лекции по матанализу и теории функции комплексного переменного в каком-нибудь ВУЗе.
0
и вообще i это сколько?
Вообще, i это мнимая единица, квадратный корень из -1.
+5
НЛО прилетело и опубликовало эту надпись здесь
Ну просто определение через квадратный корень неоднозначно, у  2 значения: i и -i. Немного софистики и как раз получается такое.
2 значения: i и -i. Немного софистики и как раз получается такое.
 2 значения: i и -i. Немного софистики и как раз получается такое.
2 значения: i и -i. Немного софистики и как раз получается такое.0
НЛО прилетело и опубликовало эту надпись здесь
Это да. Вот поэтому определение "i — такое число, квадрат которого равен -1" правильное, а через корень — нет.
А вообще, определение комплексных чисел через упорядоченную пару мне нравится больше. Тогда i = (0, 1), что вполне однозначно. А уж из этого определения можно вывести всякие арифметические свойства этого числа.
А вообще, определение комплексных чисел через упорядоченную пару мне нравится больше. Тогда i = (0, 1), что вполне однозначно. А уж из этого определения можно вывести всякие арифметические свойства этого числа.
0
Что-то в вашей версии лучше не стало: "-i — тоже такое число, квадрат которого равен -1", и хоп, у нас два одинаковых определения для двух разных чисел.
Вообще мне всегда казалось, что в определении корня пишут "неотрицательный", но быстренько повикипедив, похоже, что это только для случая, когда нам нужна функция f(x) = корень из x, а вообще определение корня как числа спокойно уживается с неоднозначностью. Поправьте, если я ошибаюсь, конечно.
Вообще мне всегда казалось, что в определении корня пишут "неотрицательный", но быстренько повикипедив, похоже, что это только для случая, когда нам нужна функция f(x) = корень из x, а вообще определение корня как числа спокойно уживается с неоднозначностью. Поправьте, если я ошибаюсь, конечно.
0
На самом деле правильное определение выглядит так: i — это число, у которого действительная часть равна нулю, а мнимая — единице.
Комплексные числа давно уже определяют конструктивно как пары действительных чисел, с дальнейшим прямым вводом арифметических операций.
Про неконструктивные определения не слышал, но среди конструктивных такое определение получается самым корректным и простым.
Даже в школе так их и учили.
Комплексные числа давно уже определяют конструктивно как пары действительных чисел, с дальнейшим прямым вводом арифметических операций.
Про неконструктивные определения не слышал, но среди конструктивных такое определение получается самым корректным и простым.
Даже в школе так их и учили.
0
Сейчас я, возможно, буду говорить глупые вещи, но разве не нужно сначала определить i, чтобы потом говорить о действительной и мнимой части? Т.е., ок, я беру ваше определение, только теперь задаю вопрос — "что такое мнимая часть"? И вам придется отвечать что-то типа "это слагаемое с коэффициентом при i", разве нет?
0
Нет, сперва вводится определение упорядоченной пары и действия над ними: сложение и умножение.


Ну и задаётся соответствие: вещественное число x равно паре (x, 0).
А затем умножим по правилам пару (0, 1) на саму себя:
Таким образом, некий объект (0, 1) в квадрате даёт нам -1. А чтобы не писать постоянно (0, 1) ему просто присвоили букву i.
Таким образом, например
С другой стороны,
Т.е. запись (3, 2) эквивалентна 3 + 2i


Ну и задаётся соответствие: вещественное число x равно паре (x, 0).
А затем умножим по правилам пару (0, 1) на саму себя:
(0, 1) * (0, 1) = (0 * 0 - 1 * 1, 1 * 0 + 0 * 1) = (-1, 0) = -1Таким образом, некий объект (0, 1) в квадрате даёт нам -1. А чтобы не писать постоянно (0, 1) ему просто присвоили букву i.
Таким образом, например
(3, 0) + (2, 0) * (0, 1) = 3 + 2*i.С другой стороны,
(3, 0) + (2, 0) * (0, 1) = (3, 0) + (2 * 0 - 0 * 1, 2 * 1 + 0 * 0) = (3, 0) + (0, 2) = (3, 2).Т.е. запись (3, 2) эквивалентна 3 + 2i
+2
Вообще мне всегда казалось, что в определении корня пишут «неотрицательный»К сожалению трюк с отбрасыванием одного из решений через неотрицательность не работает в комплексных числах ибо там числа на больше-меньше сравнивать нельзя.
0
Кстати, что-то вдруг вспомнилось, а мне в школе определяли комплексные числа как фактор-пространство кольца многочленов делённого на многочлен x^2+1!
0
Это ли не пример переусложнённого определения? Из серии «комплекс vs сетка».
0
Мне вот это определение в своё время очень понравилось, где мнимая единица выводится через "зависание" прямой на полпути во время её переворота.
0
Вы просто не знаете что такое комплексные числа. Ну и то, что арккосинусы обозначают как cos^(-1), но это мелочи. Или троллите.
Что ж, сохраню ваш мир в целости, в действительных числах решений нет.
Что ж, сохраню ваш мир в целости, в действительных числах решений нет.
+3
А что не так с 20,4*3212,5 в "екселе"?
0
Очевидно, что вы просто напросто не знакомы с комплексным числовым множеством и как следствие с основной теоремой алгебры, которая утверждает, что с комплексными числами у вас всегда будет хотя бы один ответ из множества комплексных чисел и это верно для любой функции с любыми значениями и аргументами.
А тут ваша основная ошибка. Комплексные числа лежат уже не на числовой прямой, а на числовой плоскости.
А для меня загадка как из числа лежащего на оси ox
А тут ваша основная ошибка. Комплексные числа лежат уже не на числовой прямой, а на числовой плоскости.
+1
Не-а. Уравнение ex=0 даже в комплексных числах решения не имеет.
+1
Как-то вы очень хитро применили основную теорему алгебры к тригонометрическому уравнению...
+1
Это теорема Пикара:
Любая целая функция, отличная от постоянной, принимает все (конечные) комплексные значения, за исключением, быть может, одного
0
вообще странно если написать в этом вольфраме cos(2 π-cos^(-1)(-2))
то он пишет ответ -2 радиана. т.е ответ мы получаем не число а угол что странно в принципе.
то он пишет ответ -2 радиана. т.е ответ мы получаем не число а угол что странно в принципе.
0
Какой такой Тейлор? Производная это угловой коэффициент, по-простонародному наклон графика исходной функции. По-моему, именно эта информация устаканивает в голове сие понятие.
Что касается квадратов. Квадрат там нужен для того, чтобы минимизировать не только сумму, но и максимальное отклонение. Условно говоря, равномерные погрешности {1, 1, -1} есть намного лучшая ситуация, чем {0, 0, 3} — где-то точное равенство (возможно, случайное), а где-то аномальный всплеск (скорее всего, неслучайный). Для простого суммирования эти варианты равны, а с квадратами тройка сразу выпирает.
Что касается квадратов. Квадрат там нужен для того, чтобы минимизировать не только сумму, но и максимальное отклонение. Условно говоря, равномерные погрешности {1, 1, -1} есть намного лучшая ситуация, чем {0, 0, 3} — где-то точное равенство (возможно, случайное), а где-то аномальный всплеск (скорее всего, неслучайный). Для простого суммирования эти варианты равны, а с квадратами тройка сразу выпирает.
0
Не могу согласиться. Максимальное отклонение минимизируется через минимизацию Inf нормы. Сумма модулей — за счет минимизации 1-ой нормы. А минимизация второй нормы минимизирует именно что сумму квадратов и ничего другого. Самый неинформативный критерий с потребительской точки зрения, но единственный с аналитическим решением. Вот неплохой пример с картинкой.
0
Тейлор говорил ещё и про производные высшего порядка. Про сумму квадратов да, хорошее дополнение к интуиции. Но если мы говорим про норму вектора ошибки (без возведения в квадрат), то не будет простой суммы. Будет корень из суммы квадратов.
0
по-простонародному наклон графика исходной функции
Касательной к графику исходной функции?
0
Хорошая статья. Я даже более-менее понял на визуальном уровне, что из себя представляет псевдоинверсия матрицы. Правда, именно до нее дело не дошло и повествование оборвалось на самом интересном. Не хватает более развёрнутого описания того, что делается с помощью OpenNL и как составляются системы уравнения для получения результата с изображений. А то и правда получилось как в картинке про сову.
+2
Я ничего не понял. Я знаю, что такое метод наименьших квадратов и как его использовать, я знаю, что такое линейные уравнения. Помню, что такое матрицы примерно… но:
Эта прямая должна иметь уравнение типа следующего:
/формула/
Здесь альфа и бета нам неизвестны, но известны две точки этой прямой:
/формула/
Можно записать это уравнение в матричном виде:
… а зачем? Почему вы не объяснили, зачем ее представлять в форме матрицы, если все это решается гораздо быстрее и без них? Откуда взялись единицы в матрице? Поэтому далее читать было уже совершенно не интересно, т.к. в самом начале вы задали слишком высокий уровень, пропустив базовые объяснения. Согласен с одним, все можно разжевать на пальцах, но вы это делать не стали.
ax + b = y
a*1 + b = 1
a*3 + b = 2
Вычитаем из второго первое:
2a = 1, следовательно a = 1/2
b = 1 — a = 1 — 1/2 = 1/2
Функция y = 1/2 * x + 1/2, все, зачем нужна была матрица?
Эта прямая должна иметь уравнение типа следующего:
/формула/
Здесь альфа и бета нам неизвестны, но известны две точки этой прямой:
/формула/
Можно записать это уравнение в матричном виде:
… а зачем? Почему вы не объяснили, зачем ее представлять в форме матрицы, если все это решается гораздо быстрее и без них? Откуда взялись единицы в матрице? Поэтому далее читать было уже совершенно не интересно, т.к. в самом начале вы задали слишком высокий уровень, пропустив базовые объяснения. Согласен с одним, все можно разжевать на пальцах, но вы это делать не стали.
ax + b = y
a*1 + b = 1
a*3 + b = 2
Вычитаем из второго первое:
2a = 1, следовательно a = 1/2
b = 1 — a = 1 — 1/2 = 1/2
Функция y = 1/2 * x + 1/2, все, зачем нужна была матрица?
+5
Матрица нужна затем, чтобы потом добавить других точек, где точного решения линейной системы не существует. Кроме того, оно даёт однотипную формулу для решения даже систем с двумя точками, можно подставить любые данные.
0
Если читать дальше — да, но вы это не объяснили. Мне как читателю совершенно не понятен этот перескок. Представьте, я вам говорю, что объяснить устройство ДВС очень просто, на пальцах. Смотрите: когда подается ток на свечу, она производит искру. Поэтому в четырех цилиндрах свечи работают со смещением фазы в 90 градусов… откуда фазы? почему в четырех? стоп..!
Вот такие же чувства. Полистав статью дальше, я увижу схему двигателя с 4 цилиндрами, по анимашкам возможно пойму в чем дело, но чтобы реально эффективно понять суть, мне придется снова перечитывать статью полностью с необходимым контекстом. Если не наткнусь еще раз на такую же ловушку. Иначе еще и еще раз. А это скучно, не интересно, не эффективно.
P.S. Статья хорошая, идеи отличные. Критика исключительно из-за того, что вы не реализовали заявленное в аннотации.
Вот такие же чувства. Полистав статью дальше, я увижу схему двигателя с 4 цилиндрами, по анимашкам возможно пойму в чем дело, но чтобы реально эффективно понять суть, мне придется снова перечитывать статью полностью с необходимым контекстом. Если не наткнусь еще раз на такую же ловушку. Иначе еще и еще раз. А это скучно, не интересно, не эффективно.
P.S. Статья хорошая, идеи отличные. Критика исключительно из-за того, что вы не реализовали заявленное в аннотации.
+7
Не знаю, как вы, а я читаю технические тексты в несколько проходов. И первые проходы никогда не делаю дотошными.
Грубо говоря, в первый проход я просто смотрю оглавление, во второй смотрю картинки не читая подписей к ним, затем возможно, что читаю даже подписи. И так далее. Если прекращать читать текст на первом же месте, где споткнулись, то далеко не уйти.
Грубо говоря, в первый проход я просто смотрю оглавление, во второй смотрю картинки не читая подписей к ним, затем возможно, что читаю даже подписи. И так далее. Если прекращать читать текст на первом же месте, где споткнулись, то далеко не уйти.
0
Недавно изучил очень много литературы на английском по Symfony и Doctrine. Что удивительно, в большинстве случаев понятно все с первого прохода. Второй проход нужен выборочно только для практической реализации. С моей точки зрения «на пальцах» — это когда непосвященному слушателю все понятно и интересно по мере изложения. Если не понятно или не интересно, то докладчик плохо подготовился, либо он рассказывает не своей целевой аудитории. Как сказал Стив Джобс, если вы не можете объяснить свою идею 6-илетнему ребенку, это плохая/непонятная/плохо сформулированная идея.
+5
Ну собственно, эта мысль принадлежит не Джобсу. Единственное, в чём надо убедиться, заговаривая с шестилетним ребёнком, так это то, что вы как минимум на одном языке с ним говорите. А то жестами долго будет.
0
Вполне вероятно, не спорю. Слышал из его уст на презентации, он мог цитировать.
Естественно, должен быть один язык: понятная и не оспариваемая всеми участникам диалога некая базовая терминология. Если она не заявлена, то есть какая-то предполагаемая для аудитории. Например, на хабре никому не нужно разжевывать акроним IT или сленговый термин «хабр». Входит ли в этот базис математический термин «матрица»… я сомневаюсь. Поэтому чтобы получилось «на пальцах», придется его объяснить. Не только как поле 2х2 с ячейками для хранения данных (отличная вводная), но и откуда, когда вы заполняете 4 ячейки двумя значениями вылезают единицы. И почему ниже нет матриц 3х3, а появляются 3х1. И что вы там с ними вообще дальше творите.
Либо отдельно написать статью «матрицы на пальцах», а в этой предложить всем, кто с ними не знаком, предварительно с ними ознакомиться.
Естественно, должен быть один язык: понятная и не оспариваемая всеми участникам диалога некая базовая терминология. Если она не заявлена, то есть какая-то предполагаемая для аудитории. Например, на хабре никому не нужно разжевывать акроним IT или сленговый термин «хабр». Входит ли в этот базис математический термин «матрица»… я сомневаюсь. Поэтому чтобы получилось «на пальцах», придется его объяснить. Не только как поле 2х2 с ячейками для хранения данных (отличная вводная), но и откуда, когда вы заполняете 4 ячейки двумя значениями вылезают единицы. И почему ниже нет матриц 3х3, а появляются 3х1. И что вы там с ними вообще дальше творите.
Либо отдельно написать статью «матрицы на пальцах», а в этой предложить всем, кто с ними не знаком, предварительно с ними ознакомиться.
+3
.
0
Когда человек говорит, можно попросить его объяснить непонятную часть.
Когда читаешь статью и какой-то её фрагмент не укладывается в голове, то ищешь другую статью. Если статья на непопулярную и/или нетривиальную тему — бьешься головой об стену и перечитываешь фрагмент раз за разом...
Когда читаешь статью и какой-то её фрагмент не укладывается в голове, то ищешь другую статью. Если статья на непопулярную и/или нетривиальную тему — бьешься головой об стену и перечитываешь фрагмент раз за разом...
+8
Посыл поддерживаю, но местами перегибы налицо.
Если производную порядка n определять как меру похожести на x^n, то надо перед этим определить, что такое мера похожести и объяснить, почему она разная для разных степеней (или откуда в ряду Тейлора берутся факториалы).
Отсутствие производной у модуля в одной точке и "Брр. Квадрат удобнее." не слишком убедительно хотя бы потому что есть L1-регуляризация, LASSO, LARS и так далее. Гладких функций тоже много, на квадрате свет клином не сошёлся.
Если всю математику можно объяснить «на пальцах», то хотелось бы увидеть статью про то, почему уравнение вида x^n + y^n = z^n не имеет решений в целых числах, отличных от нуля, при n > 2.
Если производную порядка n определять как меру похожести на x^n, то надо перед этим определить, что такое мера похожести и объяснить, почему она разная для разных степеней (или откуда в ряду Тейлора берутся факториалы).
Отсутствие производной у модуля в одной точке и "Брр. Квадрат удобнее." не слишком убедительно хотя бы потому что есть L1-регуляризация, LASSO, LARS и так далее. Гладких функций тоже много, на квадрате свет клином не сошёлся.
Если всю математику можно объяснить «на пальцах», то хотелось бы увидеть статью про то, почему уравнение вида x^n + y^n = z^n не имеет решений в целых числах, отличных от нуля, при n > 2.
0
Мне бы тоже хотелось увидеть такую статью. И я уверен, что это возможно. Напишете?
0
Да, всю математику можно объяснить на пальцах. Я вот уверен, что можно объяснить, скажем, теорему Хана — Банаха шестилетнему ребёнку. Более того, её и объясняют ему на пальцах: начиная с чисел и арифметики. Просто за время объяснений ребёнок успевает вырасти, закончить школу и доучиться в вузе до курсе второго-третьего. Иногда нужно очень много пальцев.
+1
Да я и не утверждаю, что всё человеческое знание можно передать за одной чашкой кофе. На самом деле, у меня просто переполнилась чаша терпения читать слишком заумно написанные тексты. Ключевое слово — слишком.
Я читаю статьи других людей (очень часто в качестве рецензента) и меня просто трясёт мелкой дрожью, когда я вижу словосочетание "симплициальный комплекс" вместо "сетка треугольников".
Я читаю статьи других людей (очень часто в качестве рецензента) и меня просто трясёт мелкой дрожью, когда я вижу словосочетание "симплициальный комплекс" вместо "сетка треугольников".
+1
Это потому, что не все одинаково хорошо умеют объяснять свои мысли. А уж педагогический талант (умение не только объяснить, но и научить) встречается ещё реже.
Одна из частых проблем — отсутствие связи с аудиторией. Человек, который говорит «симплициальный комплекс» может быть искренне убеждён, что это гораздо более понятный термин по сравнению с «сеткой треугольников». И с сожаленим должен заметить, что в русскоязычной литературе это очень распространено. Просто традиция такая — накидать побольше формул. Иначе несолидно. Дескать, кто хочет — сам пусть разбирается.
Вот и начинает казаться студентам, что математика — это набор фокусов. А ведь на самом деле в ней каждый фокус появился не просто так.
Одна из частых проблем — отсутствие связи с аудиторией. Человек, который говорит «симплициальный комплекс» может быть искренне убеждён, что это гораздо более понятный термин по сравнению с «сеткой треугольников». И с сожаленим должен заметить, что в русскоязычной литературе это очень распространено. Просто традиция такая — накидать побольше формул. Иначе несолидно. Дескать, кто хочет — сам пусть разбирается.
Вот и начинает казаться студентам, что математика — это набор фокусов. А ведь на самом деле в ней каждый фокус появился не просто так.
0
В данный момент я говорил про серьёзную научную (англоязычную, если уж на то пошло) литературу, в которой зачастую чем больше напустишь тумана, тем круче. Рецензентам тяжело резать тексты, которые они не понимают. А если и понимают примерно, то важные детали ускользают. В итоге научные журналы замусорены невесть чем.
Почитайте, что пишут люди, которые не осмеливаются назвать авторов недобросовестными:
https://www.reddit.com/r/GraphicsProgramming/comments/40m5h8/learning_calculus_required_for_rendering/
Они просто не могут прочесть статью, хотя уж конкретно это статья вообще сложной математики не использует. А написана хреново, вот непосредственные программисты и не могут воспроизвести, печаль.
А ещё куда большая печаль наступает, когда публикуют (полу-) ложные алгоритмы и они на некоторое время блокируют развитие науки в области, т.к. все рецензенты требуют сравнить результаты с данной работой, а она просто невоспроизводима....
Почитайте, что пишут люди, которые не осмеливаются назвать авторов недобросовестными:
https://www.reddit.com/r/GraphicsProgramming/comments/40m5h8/learning_calculus_required_for_rendering/
Они просто не могут прочесть статью, хотя уж конкретно это статья вообще сложной математики не использует. А написана хреново, вот непосредственные программисты и не могут воспроизвести, печаль.
А ещё куда большая печаль наступает, когда публикуют (полу-) ложные алгоритмы и они на некоторое время блокируют развитие науки в области, т.к. все рецензенты требуют сравнить результаты с данной работой, а она просто невоспроизводима....
0
Википедия — худший источник знаний по математики. Нередко даже то, что я знаю, я там понять не могу.
+3
Я могу. Все эти когомологии — совсем просто и очень даже нужно на практике. Не сейчас, но при случае сделаю.
+1
Мы ищем не просто минимум нормы, а минимум квадрата нормы. Почему? Сама точка минимума совпадает, а квадрат даёт гладкую функцию (квадратичную функцию от агрументов (alpha,beta)), в то время как просто длина даёт функцию в виде конуса, недифференцируемую в точке минимума. Брр. Квадрат удобнее.
А почему не куб или четвертая степень? :) Да и в чем проблема оптимизировать функцию, недифференцируемую в одной точке? Довольно странное обоснование. Нематематическое, неточное. Функция потерь это центральная идея метода наименьших квадратов. Когда я пытался понять, основная проблема была именно тут.
Ваша идея здравая, спасибо за статью. Но только подшлифуйте метод изложения, либо подшлифуйте аудиторию :).
+1
Потому что квадрат — это простейшая гладкая функция, отлично работает. Кое-где пользуются и другими, но это выходит за рамки обсуждения.
0
Она отлично работает, пока у вас нет выбросов. Строже говоря, пока ваши точки генерируются гауссовским распределением. Как только это нарушается, решение дает большие ошибки.
ax + b — тоже гладкая (если я не совсем забыл анализ). Но вы же не ее начали оптимизировать.
ax + b — тоже гладкая (если я не совсем забыл анализ). Но вы же не ее начали оптимизировать.
0
Абберационные точки нормально фильтруются; функция f(x) = 0 тоже гладкая, однако искать её минимумы как-то не сильно интересно.
-1
Как только мы начинаем выкидывать выбросы, так сразу исчезает возможность интерпретации результатов. Наши результаты начинают зависеть от того, что именно мы выкинули, особенно потому что квадрат быстро растёт.
Если в физике предположение о нормальности ещё хоть как-то обосновано, то в других областях сплошь и рядом у распределений толстые хвосты и МНК может намерять что угодно.
Если в физике предположение о нормальности ещё хоть как-то обосновано, то в других областях сплошь и рядом у распределений толстые хвосты и МНК может намерять что угодно.
0
Зависит от того, какие выбросы. Если они из-за того, что измерительный датчик просто отключался, то их можно и нужно фильтровать.
Дальше каждой задаче свой инструмент. Не надо взвешивать связку бананов при помощи микроскопа. МНК не являются панацеей.
Дальше каждой задаче свой инструмент. Не надо взвешивать связку бананов при помощи микроскопа. МНК не являются панацеей.
0
Нет, никакой датчик не отключался.
Мерили средний доход, пришёл Билл Гейтс, средний доход подскочил в стопиццот раз. Решили, что это выброс, поставили отсечку, выкинули Билла Гейтса.
Через месяц Билл Гейтс потратил половину своего состояния на борьбу с малярией в Африке и обеднел ниже отсечки, средний доход подскочил в полстопиццот раз.
Во всех случаях квадраты минимальные, не подкопаться.
Мерили средний доход, пришёл Билл Гейтс, средний доход подскочил в стопиццот раз. Решили, что это выброс, поставили отсечку, выкинули Билла Гейтса.
Через месяц Билл Гейтс потратил половину своего состояния на борьбу с малярией в Африке и обеднел ниже отсечки, средний доход подскочил в полстопиццот раз.
Во всех случаях квадраты минимальные, не подкопаться.
+1
Не совсем ясно, а в чём претензия к МНК-то? МНК Вам всегда даст корректный ответ — оценку параметров, минимизирующую вторую норму ошибки на измерениях. То, что в конкретной задаче такая оценка может не обладать какими-то свойствами, например, быть смещенной или не оптимальной в смысле дисперсии, то это же не проблема МНК.
0
Прямо как у классиков:
" — У нас узкая специализация. Один пришивает карман, один — проймочку, я лично пришиваю пуговицы. К пуговицам претензии есть?
К МНК претензия в том, что его используют по поводу и без. Если в позапрошлом веке приятные на ощупь гладкие функции, которые легко минимизировать гусиным пером на бумаге имели неоспоримое преимущество, то теперь и данных поболее, и выбросы в данных никто не фильтрует, и компьютеры помощнее — могут и LASSO накинуть.
" — У нас узкая специализация. Один пришивает карман, один — проймочку, я лично пришиваю пуговицы. К пуговицам претензии есть?
- Нет! Пришиты насмерть, не оторвёшь! Кто сшил костюм? Кто вместо штанов мне рукава пришил? Кто вместо рукавов мне штаны пришпандорил? Кто это сделал?"
К МНК претензия в том, что его используют по поводу и без. Если в позапрошлом веке приятные на ощупь гладкие функции, которые легко минимизировать гусиным пером на бумаге имели неоспоримое преимущество, то теперь и данных поболее, и выбросы в данных никто не фильтрует, и компьютеры помощнее — могут и LASSO накинуть.
0
Это претензия не к инструменту, а к тем, кто его использует.
По поводу остального — 1) у МНК есть аналитическое решение, в отличие от многих других, 2) в силу первого, МНК существенно быстрее.
По поводу остального — 1) у МНК есть аналитическое решение, в отличие от многих других, 2) в силу первого, МНК существенно быстрее.
0
Аналитическое решение методом наименьших квадратов, например, переопределённой системы линейных уравнений, конечно, есть. Только вот загвоздка в том, что для этого нужно искать обратную или псевдообратную матрицу, а это не так уж и быстро делается.
+1
Вы бы не могли уточнить, пожалуйста, что имеете в виду под "не так уж и быстро"?
0
Я имел в виду сложность алгоритма. Для больших матриц численно оптимизировать выйдет быстрее. Это я к тому, что из 1) не следует 2).
0
Ээ, а ещё бы провести границу между численно и аналитически… Метод сопряжённых градиентов — это численно или аналитически?
Я каждый день решаю задачи с парой десятков миллионов переменных, считается это на вполне себе бытовом компьютере минут за пять, особенно учитывая, что сопряжённые градиенты крайне хреново параллелятся...
Я каждый день решаю задачи с парой десятков миллионов переменных, считается это на вполне себе бытовом компьютере минут за пять, особенно учитывая, что сопряжённые градиенты крайне хреново параллелятся...
0
Сопряжённые градиенты — это, конечно, численно. Аналитически в данном случае — это нормальное уравнение, которое сразу даёт решение.
0
Ну, учитывая, что (теоретически) сопряжённые градиенты дают точное решение за n шагов… На практике наличие аналитического решения помогает делать быстрые численные методы.
0
Ну, учитывая, что (теоретически) сопряжённые градиенты дают точное решение за n шагов…
Если n большое, то тогда можно и обратную матрицу посчитать, пока шаги выполнятся. На практике же можно просто обеспечить приемлемую точность.
На практике наличие аналитического решения помогает делать быстрые численные методы.
Иногда помогает, иногда не очень. От задачи зависит. Нормальное уравнение к сопряжённым градиентам тоже мало отношения имеет.
0
В немного не правы. Центральная идея метода — это сама евклидова норма. А в квадрат ее возводят просто для простоты подсчета. Можно использовать хоть третью степень, хоть четвертую — результат будет тем же самым.
+1
Да, спасибо, именно это я имел в виду, когда говорил, что минимум совпадает, а квадрат удобнее.
0
Возьмем линейную регрессию для функции f(a) = ax. Пусть для простоты будет всего лишь один параметр. Пусть даны точки (0,0), (1,1), (2,2), (3,9), (4,4).
Вы хотите сказать, что минимум функции
|a-1| + |2a-2| + |3a-9| + |4a-4|
будет эквивалентен минимуму
(a-1)^2+ (2a-2)^2 + (3a-9)^2 + (4a-4)^2?
Это не так. Можно вобщем-то показать аналитически, рассмотрев sum |ax+b-y| и sum (ax+b-y)^2 где индексы пробегают x,y и a,b — переменные. Я так и не научился на хабре формулы писать...
Вы хотите сказать, что минимум функции
|a-1| + |2a-2| + |3a-9| + |4a-4|
будет эквивалентен минимуму
(a-1)^2+ (2a-2)^2 + (3a-9)^2 + (4a-4)^2?
Это не так. Можно вобщем-то показать аналитически, рассмотрев sum |ax+b-y| и sum (ax+b-y)^2 где индексы пробегают x,y и a,b — переменные. Я так и не научился на хабре формулы писать...
0
Нет, я говорил про квадрат евклидовой нормы, а не про норму l1.
0
А, понял, сорри.
Ну так почему евклидова норма? :)
Ну так почему евклидова норма? :)
+1
Евклидова норма для того, чтобы найти центр масс, который тоже находится через мнк.
Например, у вас есть две гири в один кило, разнесённые на один метр, и вы ищете точку, которая одновременно находится и в одной гире, и в другой. Норма l1 даёт бесконечное количество решений, равномерно размазанных по всему метру. Евклидова норма даст единственное решение — центр масс.
Например, у вас есть две гири в один кило, разнесённые на один метр, и вы ищете точку, которая одновременно находится и в одной гире, и в другой. Норма l1 даёт бесконечное количество решений, равномерно размазанных по всему метру. Евклидова норма даст единственное решение — центр масс.
0
Это не ответ. Многие кусочно-линейные функции дадут вам строгое решение. Да и те что дадут множество, все равно будут минимизировать функцию. Почему вы считаете, что концепция центра масс здесь будет лучше работать?
0
А? Лучше чем что именно? Давайте исходить из конкретной задачи, а то что-то слишком мутно получается.
0
Еще раз. Вы сказали что для расчета аппроксимирующей функции будете использовать квадрат L2. Но не дали обоснования, вообще. Я хочу это прояснить.
Пример задачи: я хочу предсказать значения курса доллара в те часы, когда мне он не был виден по доступным данным. L2? L1? может быть совершенно иная норма?
Пример задачи: я хочу предсказать значения курса доллара в те часы, когда мне он не был виден по доступным данным. L2? L1? может быть совершенно иная норма?
0
Мм, я не понял, что у вас есть на вход и что вы хотите на выход. А также мне нужно понять, какой функцией вы хотите приближать отсутствующие данные. Без этого разговор непредметный.
+1
Пусть будет полином третьей степени. Входные данные — пары <метка времени, курс>. Задача — восстановить функцию в тех точках времени, где нет значений курса. Классическая регрессия.
0
Отлично, осталась самая последняя деталь, которая и определит энергию системы (которая и есть энергия системы): что именно вы хотите от этого полинома третьей степени? Подойдёт ли вам ответ y = x^3? Вполне себе ответ, как мне кажется.
+1
Допустим подойдет подойдет (на локальном участке). Так какой нормой эту функцию нужно фитить?
Про энергию не понял. Мы вроде как о других моделях.
Про энергию не понял. Мы вроде как о других моделях.
0
Ммм, вы меня не поняли, я не о том. Представьте, что я вам в качестве ответа всегда даю y=x^3, вне зависимости от данных. Согласитесь, это же не то, чего вы хотите, но при этом вы нигде толком не написали, что вам нужно.
Вы можете на словах объяснить, чего именно вы хотите от функции, которая должна приближать ваши данные?
Вы можете на словах объяснить, чего именно вы хотите от функции, которая должна приближать ваши данные?
+1
Пусть я хочу минимизировать ожидаемую абсолютную ошибку отклонения предсказания от реальности. Достаточно конкретно?
0
Не-а, недостаточно. Мне по-прежнему не хватает данных. На самом деле, как только мне хватит данных, то вы сами и ответите на изначальный впрос о норме, к чему я и пытаюсь вас плавно подвести.
Давайте оставим курс доллара и кубический многочлен, это только усложняет вычисления, не привнося никакой реальной сложности. Я предлагаю рассмотреть одномерный пример, с точки зрения выбора метода аппроксимации он абсолютно равноценнен.
Представьте, что вы измеряете длину чего-то. Несколько раз. Неизвестная одна — только длина. Измерительный прибор имеет погрешность измерения, поэтому данные слегка разбросаны. Вы хотите найти одно вещественное число, которое бы удовлетворяло… Чему? Как только вы ответите на этот вопрос, ваша норма выбрана. Абсолютно то же самое и для курса доллара.
Мне не очень понятна формулировка про абсолютную ошибку ожидания от реальности. Вот, наша оценка длины — она как должна себя вести относительно данных измерения?
Давайте оставим курс доллара и кубический многочлен, это только усложняет вычисления, не привнося никакой реальной сложности. Я предлагаю рассмотреть одномерный пример, с точки зрения выбора метода аппроксимации он абсолютно равноценнен.
Представьте, что вы измеряете длину чего-то. Несколько раз. Неизвестная одна — только длина. Измерительный прибор имеет погрешность измерения, поэтому данные слегка разбросаны. Вы хотите найти одно вещественное число, которое бы удовлетворяло… Чему? Как только вы ответите на этот вопрос, ваша норма выбрана. Абсолютно то же самое и для курса доллара.
Мне не очень понятна формулировка про абсолютную ошибку ожидания от реальности. Вот, наша оценка длины — она как должна себя вести относительно данных измерения?
+1
Вы все меня толкаете к формулировке функции потерь в явном виде. Так не интересно.
Это верно. Но выбирая норму вы делаете неявное допущение о природе ошибки. В вашей задаче о линейке я бы предположил какое-то распределение ошибки, и потребовал чтобы модель, производящая точку, удовлетворяла бы принципу максимального правдоподобия.
Вы бы не смогли получить хорошую оценку в вашем примере с линейкой методом наименьших квадратов, если бы я добавил условие, что ошибка смещена. Скажем, у измерителя есть склонность к завышению.
Для предыдущего вопроса: L = E|f(xi) — yi| (E — математическое ожидание, i проходит по известным точкам)
Вы хотите найти одно вещественное число, которое бы удовлетворяло… Чему? Как только вы ответите на этот вопрос, ваша норма выбрана.
Это верно. Но выбирая норму вы делаете неявное допущение о природе ошибки. В вашей задаче о линейке я бы предположил какое-то распределение ошибки, и потребовал чтобы модель, производящая точку, удовлетворяла бы принципу максимального правдоподобия.
Вы бы не смогли получить хорошую оценку в вашем примере с линейкой методом наименьших квадратов, если бы я добавил условие, что ошибка смещена. Скажем, у измерителя есть склонность к завышению.
Для предыдущего вопроса: L = E|f(xi) — yi| (E — математическое ожидание, i проходит по известным точкам)
0
Вы не правы. Оптимизация абсолютной длины ведет к другому оптимуму. Это не "технический" момент, а довольно принципиальный. Предполагая нормальную аддитивную ошибку вокруг для аппроксимирующей функции вы приходите к квадрату евклидовой нормы.
+1
Неточность. Действительно хотел задать вопрос почему норма L2. haqreu меня поправил.
+1
Вобщем, вы правильно сказали. Извините, запутался в терминологии с непривычки. Возведение в квадрат — это техническая штука.
Просто мне кажется важным, откуда вылезает евклидова норма.
Просто мне кажется важным, откуда вылезает евклидова норма.
+1
При использовании суммы квадратов получается линейное аналитическое решение. При использовании старших степеней линейного решения так просто не получить. А точка минимума у них у всех одна и та же, так зачем усложнять?
0
Соврал, кстати. Точка минимума совпадает у квадрата и куба суммы, т.е. при возведении в степень нормы. Точки минимума у сумм квадратов или кубов будут, конечно, разные, так как это разные нормы.
+1
Спасибо за статью!
Теперь захотелось наконец-то разобраться в азах линейной алгебры, чтобы не чувствовать себя лишним на этом празднике.
Могут ли уважаемые хабраюзеры посоветовать какую-нибудь литературу либо онлайн-лекции с максимально доступным введением в линейную алгебру и, в частности, в матрицы с нуля? Возможно (и даже желательно) на английском.
Интересует практическое применение для оперирования двумерными массивами.
Теперь захотелось наконец-то разобраться в азах линейной алгебры, чтобы не чувствовать себя лишним на этом празднике.
Могут ли уважаемые хабраюзеры посоветовать какую-нибудь литературу либо онлайн-лекции с максимально доступным введением в линейную алгебру и, в частности, в матрицы с нуля? Возможно (и даже желательно) на английском.
Интересует практическое применение для оперирования двумерными массивами.
0
Как только вы пытаетесь прочитать какой-то текст, и вам кажется, что он чрезмерно сложен, то знайте, что он хреново написанУтащил в цитатник
0
НЛО прилетело и опубликовало эту надпись здесь
А вы код пробовали смотреть? А систему уравнений из кода на листочке написать?
+1
НЛО прилетело и опубликовало эту надпись здесь
0) Я никогда не отношусь со снобизмом к людям, которые знают меньше меня. Но я отношусь без особого уважения к людям, которые не выказывают к жизни интереса, к нелюбопытным людям. К тем, кто не хочет работать.
1) Если ко мне приходит студент с конкретным вопросом, пусть даже из начальной школы, я никогда не оставлю вопрос без ответа. Если студент просто говорит "я ничего не понял", то это не вопрос и показывает, что он даже не пытался работать. Он получает заслуженные два балла и уходит. Вы никакого усилия с вашей стороны не показываете, типичное поведение ленивого студента.
2) Не приписывайте мне слова, которых я не говорил. Я не говорил, что я не слушаю, когда мне непонятно. Я сразу же задаю вопросы.
3) Я рад за Ландау, но если вам нечего больше сказать, как хамить, переходя на личности и обсуждая мой русский язык, проходите, не задерживайте движение.
1) Если ко мне приходит студент с конкретным вопросом, пусть даже из начальной школы, я никогда не оставлю вопрос без ответа. Если студент просто говорит "я ничего не понял", то это не вопрос и показывает, что он даже не пытался работать. Он получает заслуженные два балла и уходит. Вы никакого усилия с вашей стороны не показываете, типичное поведение ленивого студента.
2) Не приписывайте мне слова, которых я не говорил. Я не говорил, что я не слушаю, когда мне непонятно. Я сразу же задаю вопросы.
3) Я рад за Ландау, но если вам нечего больше сказать, как хамить, переходя на личности и обсуждая мой русский язык, проходите, не задерживайте движение.
-3
НЛО прилетело и опубликовало эту надпись здесь
наука — это сообщество, и если Вы сообществу не понравитесь, если будете всячески буянить и нарушать правила сообщества, то
окажетесь за бортом, и только дома жене будете рассказывать, какой Вы молодец: например, был один метод наименьших?
квадратов, а Вы множество методов придумали! (см. название статьи: «методы наименьших квадратов»)
Не вам, гражданин, меня откуда-то-либо выкидывать, по крайней мере, к вам домой я не заходил. А в остальных местах у вас ни легитимности, ни возможности.
А методов много, объединённых одиной идеей о минимизации квадрата евклидовой нормы. Попробуйте для начала подумать, например, как решаются подобные задачи с ограничениями. Одним квадратичным штрафом, что я привёл в статье, дело не ограничивается. Ну и тому подобное. Поменьше спеси, побольше дела.
-1
НЛО прилетело и опубликовало эту надпись здесь
Но согласитесь и Вы, FransuaMaryDelone, что всё то же самое можно было бы донести без нарочито снисходительной "жалости", не прикрываясь "законами природы" (типа, кто на нас с Лёхой :)) и без пророчеств страшного будущего. Это ж всё колючие конфликтогены. По-моему, немного странно после такого обращения ожидать положительной реакции. Ну, то есть очень понижает вероятность быть услышанным. Ведь объяснение "на пальцах" не обязательно должно подразумевать тычки этими самыми пальцами в болевые точки собеседника (особенно, если взаправду жалеете человека).
+1
НЛО прилетело и опубликовало эту надпись здесь
По этому поводу есть хорошее кино "Одержимость" (Whiplash), в нём чётко показано, к чему приводит неуёмная страсть к порицаниям ради "высоких творческих достижений" (хотя у нас, конечно, не всё столь жёстко :)).
0
Мой любимый автор на хабре! Все ваши статьи я прочитал с большим удовольствием!
+1
Освещённость выравнивалась в каком цветовом пространстве?
0
Немного про квадратные уравнения.
Вася разнервничался на суде и забыл длину своего земельного участка, но помнит — его площадь равна c и что ширина его на b метров больше забытой стороны. Вася, к счастью, не совсем идиот и школьную программу кое-как помнит, давеча сын задачку принёс. Вася составляет уравнение x*(x+b) = c и вуаля, автоматически, сам того может даже и не заметив (метраж-то у участков удобный обычно) взял, да и решил квадратное уравнение.
Рабочий забыл рулетку, но нашёл длинную верёвку и линейку, а площадь помещения услышал краем уха. Ну и т.п. Какой только странной фигни не случается вот в этой самой повседневно жизни. И никогда не знаешь, где что выплывет.
Вася разнервничался на суде и забыл длину своего земельного участка, но помнит — его площадь равна c и что ширина его на b метров больше забытой стороны. Вася, к счастью, не совсем идиот и школьную программу кое-как помнит, давеча сын задачку принёс. Вася составляет уравнение x*(x+b) = c и вуаля, автоматически, сам того может даже и не заметив (метраж-то у участков удобный обычно) взял, да и решил квадратное уравнение.
Рабочий забыл рулетку, но нашёл длинную верёвку и линейку, а площадь помещения услышал краем уха. Ну и т.п. Какой только странной фигни не случается вот в этой самой повседневно жизни. И никогда не знаешь, где что выплывет.
+3
Вы сами-то верите в приведённые задачи? Когда в последний раз вам лично приходилось решать квадратное уравнение? А вашим родным?
Самая большая проблема в этих всех задачах — это ненулевой член b в уравнении ax^2 + bx + c = 0. Его-то в обычной жизни и не бывает. Померять глубину колодца, бросая камни с секундомером? Так скорость нулевая, там просто квадратный корень, а дискриминанта нет. Прикинуть дальность полёта запущенной стрелы? Так хрен, начальная скорость неизвестна...
В инженерных науках да, начальные скорости и тп известны, вот и квадратные уравнения пригождаются. В обычной жизни всё куда как прозаичнее. Рабочий даже если не сходит за рулеткой, линейкой отмерит один метр на верёвке, затем сложит её много раз, используя отмеренное как эталон. Вот вам и рулетка, и площади краем уха слышать не надо. Ну а про суд и разнервничаться, но решать при этом квадратные уравнения — даже и не смешно.
Самая большая проблема в этих всех задачах — это ненулевой член b в уравнении ax^2 + bx + c = 0. Его-то в обычной жизни и не бывает. Померять глубину колодца, бросая камни с секундомером? Так скорость нулевая, там просто квадратный корень, а дискриминанта нет. Прикинуть дальность полёта запущенной стрелы? Так хрен, начальная скорость неизвестна...
В инженерных науках да, начальные скорости и тп известны, вот и квадратные уравнения пригождаются. В обычной жизни всё куда как прозаичнее. Рабочий даже если не сходит за рулеткой, линейкой отмерит один метр на верёвке, затем сложит её много раз, используя отмеренное как эталон. Вот вам и рулетка, и площади краем уха слышать не надо. Ну а про суд и разнервничаться, но решать при этом квадратные уравнения — даже и не смешно.
-7
НЛО прилетело и опубликовало эту надпись здесь
Опять вы привели пример из профессиональной жизни. Ни истец, ни ответчик их не решают. Только гаишники и то при помощи таблицы.
0
Прикольный рассказик в тему — Зачем школьнику нужны квадратные уравнения? Там всё свелось к тому, что квадратные уравнения нужны прежде всего для развития мозга, а всякая прикладуха — как жизнь повернётся. Лично мне квадратные уравнения "на практике" пригодились при обучении программированию — их решатель была чуть ли ни первая моя программа. В этом смысле можно рассматривать квадратные уравнения как введение в алгоритмическое мышление ;)
+1
НЛО прилетело и опубликовало эту надпись здесь
Опять вы привели пример из профессиональной жизни.
А бывает вообще непрофессиональная жизнь? Вы бы сразу написали, кого вы понимаете под простыми людьми. Я вот себя очень даже простым считаю, а мне по работе (а она важная часть моей жизни) интегралы считать приходится.
0
К слову, не поясните, в какой области наук вы учёный (научный работник)? Ну там, направление работы, публикации, чем вообще занимаетесь. Из праздного любопытства.
Поскольку вброс ваш про квадратные уравнения вызвал достаточно продолжительную реакцию. Хотя, если подумать, людям, далёким от математики и точных наук большинство премудростей в жизни нафиг не нужны.
Не нужны им ни квадратные уравнения, ни все эти Ферма с их теоремами. Ни начала термодинамики, ни физхимия, ни идеальные газы, ни излучение Хокинга. Про таблицу Менделеева простой человек вспомнит только в связи с расхожей фразой "в [название продукта] сплошь химия!"
В общем-то, понятно, что квадратные уравнения ценны как этап в постижении математики, не сами по себе. Человеку обычному науки не нужны. Всё, что нужно, ему донесут из СМИ всех родов, и из общения с другими простыми людьми. И это вроде как нормально — поскольку, на самом деле, "на пальцах" (т.е., для полного невежды) ничего не объяснить. Без знания аксиоматики в математику не въехать, как и без знания английского не оценить красоту сонетов Шекспира в оригинале. Минимум знаний нужен всегда, ex nihili nihil fit, простите мою латынь.
Я, кстати видел реакцию человека девственного в смысле познаний в математике, на демонстрацию листа Мёбиуса. Так это был реальный шок — и осознание односторонности, и последствия разрезания по середине листа, и не по середине. Так что математика и рассудку повредить может, если упадёт на неподготовленный рассудок.
Пусть уже всем этим занимаются специально обученные люди. Всерьёз, в смысле. А популяризация — дело нужно, как минимум — чтобы заинтересовать потенциальных новых учёных. Которые научные работники.
Поскольку вброс ваш про квадратные уравнения вызвал достаточно продолжительную реакцию. Хотя, если подумать, людям, далёким от математики и точных наук большинство премудростей в жизни нафиг не нужны.
Не нужны им ни квадратные уравнения, ни все эти Ферма с их теоремами. Ни начала термодинамики, ни физхимия, ни идеальные газы, ни излучение Хокинга. Про таблицу Менделеева простой человек вспомнит только в связи с расхожей фразой "в [название продукта] сплошь химия!"
В общем-то, понятно, что квадратные уравнения ценны как этап в постижении математики, не сами по себе. Человеку обычному науки не нужны. Всё, что нужно, ему донесут из СМИ всех родов, и из общения с другими простыми людьми. И это вроде как нормально — поскольку, на самом деле, "на пальцах" (т.е., для полного невежды) ничего не объяснить. Без знания аксиоматики в математику не въехать, как и без знания английского не оценить красоту сонетов Шекспира в оригинале. Минимум знаний нужен всегда, ex nihili nihil fit, простите мою латынь.
Я, кстати видел реакцию человека девственного в смысле познаний в математике, на демонстрацию листа Мёбиуса. Так это был реальный шок — и осознание односторонности, и последствия разрезания по середине листа, и не по середине. Так что математика и рассудку повредить может, если упадёт на неподготовленный рассудок.
Пусть уже всем этим занимаются специально обученные люди. Всерьёз, в смысле. А популяризация — дело нужно, как минимум — чтобы заинтересовать потенциальных новых учёных. Которые научные работники.
+2
Слушайте, но это же не вброс, серьезно) Автор просто говорит, что это такой метод познания, условно говоря — сделать глупое лицо и сказать "я не понимаю, зачем это нужно", чтобы потом получить простой пример — и понять) Нигде же не было фразы "квадратные уравнения не нужны, давайте жечь учебники и выть на луну".
То есть среднестатистический школьник на уроке о квадратных уравнениях должен иметь возможность поднять руку, встать и честно заявить "я не понимаю, зачем эти штуки мне нужны, объясните, пожалуйста?". После чего преподаватель рассказывает ему о компьютерной графике, у школьника загораются глаза, и вернувшись домой, он закапывается в книжки и добирается до линейной алгебрыи пишет свой OpenGL. Сейчас школы так не делают, и это плохо, по-моему — в результате, когда среднестатистические школьники потом становятся среднестатистическими родителями, у них вечные проблемы с ответом на вопрос "а зачем моим детям вообще учить математику?", на который они отвечают что-то в духе "ну, чтобы мозги упражнять".
И все то же самое применимо к взрослым людям и чуть более замороченной математике. Вот читал я статью вчера, и не мог понять — нафига мне нужен minimum description length principle? Но я нашел более простую статью и все понял)
То есть среднестатистический школьник на уроке о квадратных уравнениях должен иметь возможность поднять руку, встать и честно заявить "я не понимаю, зачем эти штуки мне нужны, объясните, пожалуйста?". После чего преподаватель рассказывает ему о компьютерной графике, у школьника загораются глаза, и вернувшись домой, он закапывается в книжки и добирается до линейной алгебры
И все то же самое применимо к взрослым людям и чуть более замороченной математике. Вот читал я статью вчера, и не мог понять — нафига мне нужен minimum description length principle? Но я нашел более простую статью и все понял)
+2
Вброс это провокационное заявление (необязательно в негативном смысле). Подтверждение — приведённая ниже цитата из OP:
Что это, как не вброс? (вопрос риторический)
Математика — это серия фокусов. Математики стараются запутать и запугать публику; там, где нет замешательства, нет репутации, нет авторитета. Да, это престижно говорить как можно более абстрактным языком, что есть по себе полная чушь.
Что это, как не вброс? (вопрос риторический)
0
Да, большое спасибо. Мои студенты избегают математики как огня именно потому, что им в принципе не объясняли, что это всё полезно. Моё основное утверждение состоит в том, что при обучении школьников и студентов всегда можно привести вполне говорящий пример, зачем это всё нужно. Лично я окончил матмех СПбГУ, отделение чистая математика. Да, меня обучали топологии, только за пять лет мне не привели ни единого примера, зачем нужна топология. Зачем вон те самые когомологии, о которых спросили выше. А ведь они очень даже нужны, чтобы 3Д модели текстурировать, и объясняется там всё куда как прозаичнее и понятнее, нежели на приведённой выше ссылке.
Именно поэтому я стараюсь никогда не читать лекции из разряда: "Ну это же фундаментально! Пригодится потом!" Нет. Градиент? Окей, градиентный спуск, минимизация усилий. Ковариации? Не вопрос, вот вам лабораторная по распознаванию звука. И тому подобное.
И читая школьные и вузовские учебники, у меня волосы дыбом встают, я вообще не понимаю, как я сам-то через это продрался. А мне было отчаянно скучно считать про две трубы в бассейне именно потому, что это просто лицемерно — давать словесное определение задачи, когда оно лишено житейского смысла. Давайте сразу уравнение, его и решим. Или приводите нормальные примеры.
Именно поэтому я стараюсь никогда не читать лекции из разряда: "Ну это же фундаментально! Пригодится потом!" Нет. Градиент? Окей, градиентный спуск, минимизация усилий. Ковариации? Не вопрос, вот вам лабораторная по распознаванию звука. И тому подобное.
И читая школьные и вузовские учебники, у меня волосы дыбом встают, я вообще не понимаю, как я сам-то через это продрался. А мне было отчаянно скучно считать про две трубы в бассейне именно потому, что это просто лицемерно — давать словесное определение задачи, когда оно лишено житейского смысла. Давайте сразу уравнение, его и решим. Или приводите нормальные примеры.
+3
Я немного удивлен количеству людей в комментах, которые из вашей фразы сделали прямо противоположные выводы) В любом случае, пишите еще, и побольше таких преподавателей)
(напальцево-практический подход недавно очень порадовал вот в этом курсе на Курсере. Кому, казалось бы, легче от того, что функцию Бесселя можно увидеть, если покрутить свободным концом веревки? Мне, например, очень)
(напальцево-практический подход недавно очень порадовал вот в этом курсе на Курсере. Кому, казалось бы, легче от того, что функцию Бесселя можно увидеть, если покрутить свободным концом веревки? Мне, например, очень)
+3
Помню, что на первом курсе спросил — а зачем матрице детерминант. Мне сказали — "много зачем!" и я отстал.
+4
Очень показательный пример, спасибо.
0
В аналогичной ситуации я потребовал конкретных примеров. Получил (чтобы выяснить, не являются ли строки или столбцы линейно зависимыми; для решения системы линейных уравнений и т.д.).
От преподавателя зависит.
От преподавателя зависит.
0
Это равенство определителя нулю, весьма ограниченное применение. А ещё?
0
Чем, простите, ограниченное?
В моём комментарии упомянуто два использования детерминанта. Третье, навскидку — вычисление обратной матрицы.
В моём комментарии упомянуто два использования детерминанта. Третье, навскидку — вычисление обратной матрицы.
0
Из ваших слов мне кажется наиболее вероятным, что с определителями/собственными числами вы имели дело только на семинаре по линейной алгебре на первом курсе вуза. Почему мне так кажется?
Потому, что вы предлагаете проверить детерминант на строгое равенство нулю (линейная зависимость и остальные ваши применения, типа обратной матрицы). А что если он равен не нулю, а 1e-10? А если 1e10?
Именно поэтому мне кажется, что вы оперируете этими понятиями на уровне синтаксическом: вам определили алфавит и набор грамматических правил на нём. А картинки, которая объясняет что это такое в голове у вас нет. Применения вытекают только из того, чем объект является. А этого понимания, опять же, насколько я понимаю, у вас нет.
Потому, что вы предлагаете проверить детерминант на строгое равенство нулю (линейная зависимость и остальные ваши применения, типа обратной матрицы). А что если он равен не нулю, а 1e-10? А если 1e10?
Именно поэтому мне кажется, что вы оперируете этими понятиями на уровне синтаксическом: вам определили алфавит и набор грамматических правил на нём. А картинки, которая объясняет что это такое в голове у вас нет. Применения вытекают только из того, чем объект является. А этого понимания, опять же, насколько я понимаю, у вас нет.
-1
Громкие слова для человека, который называет себя учёным, но по великой скромности не хочет продемонстрировать хотя бы одну научную работу.
Есть у меня понимание или нет, простите, выясняется исключительно практическим путём — когда мне требуется решить задачу, в которой нужен детерминант. Или объяснить кому-нибудь, что это такое — в картинках и схемах, как нам в своё время объясняли.
Ноль — специальное значение детерминанта, при котором у его матрицы есть вполне конкретные свойства. Например, что у неё отсутствует обратная. "Почти ноль" или "совсем не ноль" — это все прочие случаи. Ничего, что я объясняю очевидное?
Надеюсь, что вы не скажете своим студентам "если у матрицы определитель ничтожно мал, можно считать, что обратной матрицы не существует".
Есть у меня понимание или нет, простите, выясняется исключительно практическим путём — когда мне требуется решить задачу, в которой нужен детерминант. Или объяснить кому-нибудь, что это такое — в картинках и схемах, как нам в своё время объясняли.
Ноль — специальное значение детерминанта, при котором у его матрицы есть вполне конкретные свойства. Например, что у неё отсутствует обратная. "Почти ноль" или "совсем не ноль" — это все прочие случаи. Ничего, что я объясняю очевидное?
Надеюсь, что вы не скажете своим студентам "если у матрицы определитель ничтожно мал, можно считать, что обратной матрицы не существует".
0
Громкие слова для человека, который называет себя учёным, но по великой скромности не хочет продемонстрировать хотя бы одну научную работу.
Голубчик, тема статьи и обсуждения — линейная алгебра, а не моя карьера. Не переходите на личности. Мне глубоко всё равно, что вы лично считаете меня болтуном и хвастуном, положение дел в обучении от этого не меняется.
Ноль — специальное значение детерминанта, при котором у его матрицы есть вполне конкретные свойства. Например, что у неё отсутствует обратная. "Почти ноль" или "совсем не ноль" — это все прочие случаи. Ничего, что я объясняю очевидное?
Нет никаких специальных значений. Есть конкретные задачи, которые нужно решать, используя имеющийся инструментарий. Выбор инструментария обуславливается пониманием того, что из себя представляет каждый инструмент.
А в данном случае вы вообще забываете про стабильность численных вычислений. Видимо, просто потому, что это не входит в круг ваших интересов/занятий, а в вузе вам про это не рассказали.
-1
Не переходите на личности.
"Врачу, исцелися сам".
Мне глубоко всё равно, что вы лично считаете меня болтуном и хвастуном,
Из чего следует, что я считаю вас болтуном и хвастуном? Вообще-то я просто считаю вас человеком, который научной работой не занимается, а занимается преподаванием. Заметьте: не употреблено ни единого уничижительного слова.
Не играйте в телепата, пожалуйста. Хотите знать, что дуамет собеседник — просто спросите.
Нет никаких специальных значений.
Ноль для детерминанта — вполне специальное значение. При нём у матрицы вполне конкретные свойства, которых не наблюдается при других значениях.
Есть конкретные задачи, которые нужно решать, используя имеющийся инструментарий.
Это утверждение не противоречит утверждению, о том, что ноль для определителя матрицы — специальное значение.
А в данном случае вы вообще забываете про стабильность численных вычислений.
Трудно забывать о том, о чём и разговор-то не шёл.
0
Трудно забывать о том, о чём и разговор-то не шёл.
Здрасте приехали. Всю дорогу тут идёт речь о реальных применениях математики, а вы так и не сумели привести ни одного.
-1
Посмотрите, на что я отвечал, когда речь зашла о том, "зачем матрице детерминант". Каким боком тут "реальное применение математики"?
Можно далеко не ходить. В своё время я занимался неэмпирическими квантовохимическими расчётами. Сейчас в т.ч. занимаюсь криптографическими алгоритмами. Во вполне практической области, ПО пишу.
Это подходит под "реальное применение математики"?
Если речь про использование математики, отличной от арифметики под управлением калькулятора, т.н. простыми людьми, то на эту тему я достаточно подробно высказался выше.
Можно далеко не ходить. В своё время я занимался неэмпирическими квантовохимическими расчётами. Сейчас в т.ч. занимаюсь криптографическими алгоритмами. Во вполне практической области, ПО пишу.
Это подходит под "реальное применение математики"?
Если речь про использование математики, отличной от арифметики под управлением калькулятора, т.н. простыми людьми, то на эту тему я достаточно подробно высказался выше.
0
Спасибо, конечно, но мне неинтересно знать, чем конкретно вы занимаетесь. Я вас об этом и не спрашивал, прошу заметить.
Именно на вопрос "зачем" и нельзя отвечать "если ноль, то матрица плохая, а если не ноль, то хорошая". Ваш ответ на вопрос "зачем" бесполезен.
Этот самый детерминант (вкупе с другими критериями) и определяет, что такое плохая. В том числе и порядок, не просто "А плохая, Б плохая". А ещё и отношение "А лучше Б".
Именно на вопрос "зачем" и нельзя отвечать "если ноль, то матрица плохая, а если не ноль, то хорошая". Ваш ответ на вопрос "зачем" бесполезен.
Этот самый детерминант (вкупе с другими критериями) и определяет, что такое плохая. В том числе и порядок, не просто "А плохая, Б плохая". А ещё и отношение "А лучше Б".
0
То есть ответа, подходит ли упомянутое мной использование математики под "реальное применение математики", не будет?
Абстрагируйтесь от меня и ответьте тогда на вопрос: подготовка данных, использование программы для квантовохимического расчёта ab initio и обработка полученных данных относится к реальному применению математики?
Товарищ выше уже упомянул: вы выносите суждения с формальной, строгой части (где чётко определяется, что такое определитель, каковы его свойства и пр.) с точки зрения прикладного применения. Что попросту лишено смысла.
Абстрагируйтесь от меня и ответьте тогда на вопрос: подготовка данных, использование программы для квантовохимического расчёта ab initio и обработка полученных данных относится к реальному применению математики?
Товарищ выше уже упомянул: вы выносите суждения с формальной, строгой части (где чётко определяется, что такое определитель, каковы его свойства и пр.) с точки зрения прикладного применения. Что попросту лишено смысла.
0
НЛО прилетело и опубликовало эту надпись здесь
К теме обсуждения (определитель, а более глобально преподавание абстракций) ваша карьера относится так же, как если бы я заявил, что могу проплыть триста метров баттерфляем.
С вами я дискуссию закрою, у меня нет больше времени. Для тех, кто прочитает: вся статья про то, что самой по себе абстрактной математики, без наглядных иллюстраций, в школе быть не должно.
А определитель — это мера того, насколько линейное отображение далеко от единичного. Отсюда вытекают применения.
С вами я дискуссию закрою, у меня нет больше времени. Для тех, кто прочитает: вся статья про то, что самой по себе абстрактной математики, без наглядных иллюстраций, в школе быть не должно.
А определитель — это мера того, насколько линейное отображение далеко от единичного. Отсюда вытекают применения.
0
При чём тут моя карьера, а?
Повторяю свой вопрос: подготовка данных, использование программы для квантовохимического расчёта ab initio и обработка полученных данных относится к реальному применению математики? — Заметьте, никакой привязки ни к чьей карьере.
У вас привычка уклоняться от ответов, когда ничто не мешает их дать. Боитесь показать, что вы, как и все люди, можете ошибаться? Или ещё каким-то образом повредить свой нимб?
Впрочем, уже неважно, картина вполне понятна, спасибо. "Садитесь, два".
Повторяю свой вопрос: подготовка данных, использование программы для квантовохимического расчёта ab initio и обработка полученных данных относится к реальному применению математики? — Заметьте, никакой привязки ни к чьей карьере.
У вас привычка уклоняться от ответов, когда ничто не мешает их дать. Боитесь показать, что вы, как и все люди, можете ошибаться? Или ещё каким-то образом повредить свой нимб?
Впрочем, уже неважно, картина вполне понятна, спасибо. "Садитесь, два".
+1
Слушайте, у меня действительно мало времени с вами флейм разводить, мне куда как полезнее ответить на вопросы рецензентов по моей монографии, но вы настолько неумело троллите, что я вас всё же покормлю.
Я не знаю, относится ся ли использование программы или даже пусть её написание к реальному применению математики. Может да, а может и нет, мне не хватает данных, чтобы ответить на этот вопрос.
Только я даже отвечать на него не хочу, так как к теме обсуждения, напоминаю, определитель, а более глобально преподавание абстракций, это не относится никаким боком.
Я не знаю, относится ся ли использование программы или даже пусть её написание к реальному применению математики. Может да, а может и нет, мне не хватает данных, чтобы ответить на этот вопрос.
Только я даже отвечать на него не хочу, так как к теме обсуждения, напоминаю, определитель, а более глобально преподавание абстракций, это не относится никаким боком.
-1
но вы настолько неумело троллите, что я вас всё же покормлю
Это кто недавно просил не переходить на личности?
Я и не начинал ещё вас троллить, если что. Нет смысла — вы сами по каждому моменту сливаетесь в полный рост. Даже скучно как-то.
Я не знаю, относится ся ли использование программы или даже пусть её написание к реальному применению математики. Может да, а может и нет, мне не хватает данных, чтобы ответить на этот вопрос.
Ну наконец-то.
Нет чтобы сразу ответить, чесслово.
0
Ну я ответил, что не знаю, относится ли ваша работа к практическому применению математики, дальше-то какой вы вывод делаете? :)
0
Делаю вывод, что не знаете. По вашим же словам, недостаточно информации.
0
Голубчик, ну не томите же, не томите! Скажите, зачем вам нужно было знать, могу ли я классифицировать вашу деятельность? Только очень вас прошу, пишите мысли полностью, а не кусочками!
На всякий случай напоминаю тему дискуссии.
На всякий случай напоминаю тему дискуссии.
0
Томитесь в неведении — то, что мне было нужно, я узнал. А потому не отвлекаю вас более от важных дел.
0
Слив засчитан.
-2
Ваши студенты правда читают этот тред? Тогда непонятно, кому слив засчитан на самом деле. :) Будем здоровы!
0
Безусловно, наикрепчайшего вам здоровья! И за моих студентов и меня вы не беспокойтесь, всё будет отлично.
Мне только очень жаль, что ни одной полной мысли вы так нигде и не оформили. В итоге флейма вагон, а вынести (например, мне) из беседы нечего.
Мне только очень жаль, что ни одной полной мысли вы так нигде и не оформили. В итоге флейма вагон, а вынести (например, мне) из беседы нечего.
-2
Мне только очень жаль, что ни одной полной мысли вы так нигде и не оформили.
Это не более, чем ваше мнение. Ну не обязан я формулировать всё исключительно в доступной именно для вас форме.
Но, раз тут я говорю ни много ни мало с преподавателем, добавлю немного за химию и математику.
Мне повезло с преподавателями (по химии, физике, математике). Ещё со школы попадались люди, которые умели так всё изложить, что хотелось узнать больше. Имена, если кому интересно, я назову.
Плюс книги (полагаю, все, кто любит математику, знают имена Бориса Кордемского, Щепана Еланьского, Мартина Гарднера, Сергея Боброва, и других популяризаторов).
Одна общая у них черта: они никогда не принижают собственный предмет, даже в шутку. От них услышать что-нибудь вроде
Математика — это серия фокусов. Математики стараются запутать и запугать публику; там, где нет замешательства, нет репутации, нет авторитета. Да, это престижно говорить как можно более абстрактным языком, что есть по себе полная чушь.
было абсолютно невозможно. За что их и уважаю.
Кстати, книги упомянутых полезно читать и перечитывать студентам, которые боятся математики.
+1
Неужели вы так и не поняли, что конкретно к математике у меня нет ни малейшей претензии? У меня есть очень большие претензии к тому, как она используется. Математик — слово мистическое для большинства аудитории. Им быть престижно, потому что большинство аудитории совсем не понимает, чем этот самый математик занимается. И это порочный круг, это плодит всё больше и больше недобросовестности, утапливая понимание в океане умных слов. Гарднер безусловный молодец. И теорема Ферма нужна, и квадратные уравнения. Только не в том формате, который в данный момент широчайшим образом используется в школе и в вузах. Если лично вам повезло с преподавателями — это прекрасно. Только вы сами использовали слово повезло. А везти не должно, это должно быть систематическим результатом.
0
Неужели вы так и не поняли, что конкретно к математике у меня нет ни малейшей претензии?
Математика — это серия фокусов. Математики стараются запутать и запугать публику; там, где нет замешательства, нет репутации, нет авторитета. Да, это престижно говорить как можно более абстрактным языком, что есть по себе полная чушь.
Скажите, в приведённых выше цитатах слово "математика" вы используете в одном и том же смысле?
А везти не должно, это должно быть систематическим результатом.
Вы всегда выбирали преподавателя сами, находя лучшего из имеющихся? Заведомо зная, что он научит именно тому, что вам нужно?
Поделитесь умением, мэтр.
+1
Скажите, в приведённых выше цитатах слово "математика" вы используете в одном и том же смысле?
Нет. В одном случае я говорю про науку, которую безмерно уважаю, в другом про то, как она выглядит для обывателя и как она используется недобросовестными (зачастую неосознанно недобросовестными) людьми для своего личного карьерного роста.
Вы всегда выбирали преподавателя сами, находя лучшего из имеющихся? Заведомо зная, что он научит именно тому, что вам нужно?
Разумеется, нет. Я ел то, что давали. И зачастую давали пищевой наполнитель, а не еду. И весь мой дискурс ровно о том, что это ненормальная ситуация, что нужно её исправлять.
Поделитесь умением, мэтр.
Пожалуйста, вздохните глубоко, и перечитайте ещё раз всё, что тут написано. Вы боретесь с тем, что вы же сами и придумали. Не ищите в моих словах того, чего там нет. Ну и чуточку больше уважения к собеседнику тоже не помешает: несмотря на вашу упёртость и прямо скажем, не очень вежливые заявления, я стараюсь аккуратно до вас доносить свою мысль. Не всегда получается, иногда меня тоже заносит, но я стараюсь. Постарйтесь и вы, пожалуйста.
0
Разумеется, нет. Я ел то, что давали.
Тогда как понимать вот это -
Только вы сами использовали слово повезло. А везти не должно, это должно быть систематическим результатом.
в ответ на фразу "повезло с преподавателями"?
(вопрос риторический, если что)
Вы боретесь с тем, что вы же сами и придумали. [и всё остальное]
"Врачу, исцелися сам".
Нелепо давать добрые советы дважды, но что поделать.
0
Тогда как понимать вот это -
Мне казалось, что я предельно ясно написал, давайте другими словами: я считаю, что в данный момент отрасль больна. Что преподавательская масса должна улучшиться, чтобы не нужно было везения для получения качественного образования.
Это включает в себя не только школу и вуз, это включает в себя и научные публикации, которые пишутся языком, доступным лишь узкому кругу посвящённых. Причём зачастую ещё и настолько, что этот узкий круг посвящённых сам себя и рецензирует, поднимая свой личный карьерный индекс, при этом допуская в своих работах невоспроизводимые, а то и просто ложные результаты.
(вопрос риторический, если что)
Ну вот пожалуйста, непосредственно после просьбы не хамить вы опять за своё. Зачем?
0
я считаю, что в данный момент отрасль больна.
Увы, не поспоришь. тут согласие по всем практически пунктам. Однако я говорил, во всех своих комментариях, о математике как о науке — и добросовестных учёных.
Возможно, следует уточнять контекст, прежде чем набрасываться с резкими высказываниями.
Ну вот пожалуйста, непосредственно после просьбы не хамить вы опять за своё. Зачем?
Я могу задать вам тот же вопрос.
К слову о позитивном: кого вы можете посоветовать как добросовестного математика-популяризатора нашего времени?
0
Я могу задать вам тот же вопрос.
Прошу заметить, что это вы не уточнили контекст и ринулись в бой с миражом, накручивая себя сильнее и сильнее, с первых же комментариев требуя подтверждения моей карьеры и прочего.
Раз уж мы закрываем весь этот флейм, и если вам всё ещё интересно, можете полистать мою монографию, которую я написал для получения хабилитации. К непосредственно текстам моих статей, подозреваю, у вас не будет доступа, т.к. журналы их продают. К слову сказать, вся эта информация вполне доступна, мои полные данные висят прямо у меня в профайле, не здесь, так на гитхабе.
К слову о позитивном: кого вы можете посоветовать как добросовестного математика-популяризатора нашего времени?
К сожалению, не знаю. И буду крайне благодарен за любые ссылки. Могу привести вот этот комикс, его автор молодец.
0
НЛО прилетело и опубликовало эту надпись здесь
А определитель — это мера того, насколько линейное отображение далеко от единичного.
Что-то здесь не то. "Мера того, насколько линейное отображение далеко от единичного" — это какая-нибудь норма матрицы A-E, например, используется при ответе на вопрос "насколько точно мы определили ориентацию камеры". Определитель, если применять его к отображениям — объём параллелепипеда, являющегося образом единичного куба. Ничего общего.
0
Не совсем ничего общего. Если этот объём сильно меньше объёма изначального куба, то есть немаленькая вероятность получить очень плохую обусловленность. Самого определителя для этого не хватает, я согласен, потому я выше и писал, что вкупе с другими критериями, такими как след и тп.
0
А, я понял. Это я дебил, у меня профессиональная деформация, мне настолько много нужно считать всякое, не зависящее от вращений, что у меня в мозгу любое вращение — это единичное преобразование :)
0
Вы подходите с позиции строгой математики. Вам аппонент — с позиции прикладного применения и реальных расчётов. Если СЛАУ плохо обусловлена — с практической точки зрения, по факту, это так же плохо, как если бы определитель был нулём.
0
Согласен.
В таких случаях нужно начинать разговор с того, что определять контекст: "а если мы говорим про..." — и далее станет ясно, при чём тут очень малое значение детерминанта. После этого и поводов для спора не будет.
В таких случаях нужно начинать разговор с того, что определять контекст: "а если мы говорим про..." — и далее станет ясно, при чём тут очень малое значение детерминанта. После этого и поводов для спора не будет.
0
Я не совсем согласен с самим существованием "позиции строгой математики". Математика не существует сама по себе, она существует потому что нужно лечить людей и строить дома. И вполне себе строгая математика используется для оценки погрешности вычислений...
-1
Т.е. все эти доказательства Великой Теоремы Ферма, поиски закономерности в простых числах, все эти числа Грэма и т.д. и т.п. нафиг не нужны человечеству?
0
Гражданин, если вы не видите практической пользы в поисках закономерностей в простых числах, то это лично ваши пробелы в образовании. Закономерности ищут не для поиска закономерностей, а для решения конкретных прикладных задач. Не надо мистифицировать науку, а?
0
Гражданин, если вы не видите практической пользы в поисках закономерностей в простых числах, то это лично ваши пробелы в образовании.
Я-то как раз вижу, о чём и писал. Прекращайте уже приписывать собеседнику чёрт-те что, если по существу вам нечего сказать.
Для вашей эрудиции: как побочный продукт, из вроде бы чисто умозрительного поиска закономерностей в простых числах, мы сейчас имеет системы шифрования с открытым ключом. Очень даже практическое, вполне востребованное применение. Это к слову о пользе фундаментальной науки.
Sapienti sat.
0
К применениям равенства определителя нулю ещё можно добавить поиск собственных значений (откуда следует много дальнейших применений), проверка наличия кратных корней многочлена или общих корней двух многочленов… Из применений самого значения детерминанта сходу вспоминаются только вычисление ориентации базиса и якобиан системы функций — для замены переменных в кратных интегралах.
Но важнее то, что из-за нескольких свойств (полилинейность, антисимметричность, мультипликативность) с детерминантом очень удобно работать. Когда что-нибудь хорошо выражается, скажем, через перманент (например, число возможных паросочетаний), мы отмечаем это, как курьёзный факт, и ищем другие подходы.
Но важнее то, что из-за нескольких свойств (полилинейность, антисимметричность, мультипликативность) с детерминантом очень удобно работать. Когда что-нибудь хорошо выражается, скажем, через перманент (например, число возможных паросочетаний), мы отмечаем это, как курьёзный факт, и ищем другие подходы.
0
Я к тому моменту уже представлял и обратные матрицы, и всё такое базовое. Так что этот ответ меня бы совершенно не устроил.
Меня больше интересовало, как так вышло, что хитрым образом вычисляемый скаляр вдруг оказывается таким важным для матриц, в чём тут глубинный смысл. К сожалению, на такие вопросы ответить, вроде как, сложнее, чем на "где используется".
Меня больше интересовало, как так вышло, что хитрым образом вычисляемый скаляр вдруг оказывается таким важным для матриц, в чём тут глубинный смысл. К сожалению, на такие вопросы ответить, вроде как, сложнее, чем на "где используется".
0
Давайте я вам расскажу, как работает общение в человеческом обществе именно на этом примере. Вот вы читаете текст, увидели слово, которое вам не нравится, в данном случае "учёный". Тут есть два варианта развития событий:
1) Вы пишете: "Вам не кажется, что это слово звучит довольно помпезно?" На это вы получаете от меня ответ: "Хм, действительно. Прошу прощения, никогда не доводилось говорить о моей работе на русском языке, вот и промахи в терминологии. Ни в коем случае не собирался ставить себя в один ряд с фигурами калибра Ладау."
2) Вы пишете про учёных собак и требуете список публикаций. На что получаете предложение прогуляться.
Конкретно вы выбираете скорее второй путь. А первый куда как продуктивнее. И не раздражён никто, и текст поправлен, один профит. Список моих публикаций находится в гугле за пару минут максимум, вы даже этого не попытались сделать, только начали громогласно его требовать прямо вот сюда.
В общем, проходите, гражданин, не засоряйте эфир.
1) Вы пишете: "Вам не кажется, что это слово звучит довольно помпезно?" На это вы получаете от меня ответ: "Хм, действительно. Прошу прощения, никогда не доводилось говорить о моей работе на русском языке, вот и промахи в терминологии. Ни в коем случае не собирался ставить себя в один ряд с фигурами калибра Ладау."
2) Вы пишете про учёных собак и требуете список публикаций. На что получаете предложение прогуляться.
Конкретно вы выбираете скорее второй путь. А первый куда как продуктивнее. И не раздражён никто, и текст поправлен, один профит. Список моих публикаций находится в гугле за пару минут максимум, вы даже этого не попытались сделать, только начали громогласно его требовать прямо вот сюда.
В общем, проходите, гражданин, не засоряйте эфир.
-1
Вот вы читаете текст, увидели слово, которое вам не нравится, в данном случае "учёный".
Это вы решили, что оно мне не нравится? Логично бы меня спрашивать, а не делать за меня выводы, верно?
Вы пишете про учёных собак и требуете список публикаций. На что получаете предложение прогуляться.
Про учёных собак писал не я — это раз. Требовать я не требовал — это два. Поинтересовался, ведёте ли вы научную работу — в смысле, являетесь ли научным работником. Где вы там рассмотрели требование?
Достаточно было просто ответить "нет, не являюсь".
Пока что могу сделать вывод, что вы научной деятельностью не занимаетесь, только преподаванием. Верно?
-1
Из того, что вы-таки меня поправляете с этими научными работниками, я и делаю вывод, что слово учёный из моих уст вам не нравится. Я ошибся?
Про чистое преподавание неверно.
Про чистое преподавание неверно.
-1
НЛО прилетело и опубликовало эту надпись здесь
У автора там в середине промелькнула картинка, где минимизировались расстояния от точек до искомой прямой по перпендикуляру. Это ошибка. В методе МНК минимизируются не расстояния по перпендикуляру, а разница между модельным значением и истинным значением при одном и том же иксе. Другими словами, минимизируются не красные отрезки, а зеленые:


+1
Они отличаются умножением на константу, так что это то же самое.
0
Минимизация F(p) = Sum (yi — f(xi, p))^2 -> min подразумевает именно зеленые линии.
0
Это ни разу не "то же самое". Рассмотрите четыре точки в вершинах высокого и узкого прямоугольника. Минимизация красных линий дала бы вам вертикальную прямую, минимизация зелёных — даст горизонтальную. То же самое будет если вы возьмёте не одну точку, а "рой" точек.
Проблема в том, что ваша "константа" зависит от угла наклона прямой! Вот для уравнения "y = x + Δ" (при неизменном наклоне прямой) это действительно неважно — но в статье-то речь не об этом!
Проблема в том, что ваша "константа" зависит от угла наклона прямой! Вот для уравнения "y = x + Δ" (при неизменном наклоне прямой) это действительно неважно — но в статье-то речь не об этом!
+1
"Константа" зависит от угла наклона прямой. В случае минимизации зелёных линий оптимальная прямая будет иметь несколько меньший угол наклона, чем в случае минимизации красных. Так что это не то же самое.
0
Да, у меня неточность, спасибо!
0
"Очевидно, что ошибка(длина вектора разности (i+j)- b) минимизируется, когда вектор e ортогонален плоскости, натянутой на векторы i и j."
вот здесь ошибка, потому так и получилось как на рисунке
по факту по представленной автором иллюстрации, ошибка = длине ( разности векторов (i+j) и b ) минимальна, когда вектор e = (i+j)-b перпендикулярен вектору b (а не плоскости, натянутой на векторы i и j.)
вот здесь ошибка, потому так и получилось как на рисунке
по факту по представленной автором иллюстрации, ошибка = длине ( разности векторов (i+j) и b ) минимальна, когда вектор e = (i+j)-b перпендикулярен вектору b (а не плоскости, натянутой на векторы i и j.)
0
Завис на фразе "Можно записать это уравнение в матричном виде", пока не вспомнил правило перемножения матриц. Как-то не вполне вяжется со следующей фразой: "Матрица это не что иное, как двумерный массив. Это способ хранения данных, более никаких значений ему придавать не стоит.". Значит всё таки не только способ записи, но и определённые законы? И как определить, когда "можно записать в матричном виде", а когда — нельзя?
+2
Ох. Зависит. Для меня лично никаких операций над двумерным массивом делать нельзя, пока вы не вложили смысл в то, что в нём хранится. Например, весьма распространено выражать точки через вектор-столбцы. Казалось бы, в общем и целом сложение может быть определено для матриц. А вот для точек сложение не определено. Таким образом, лично я считаю, что первично определить, что за объект мы храним в двумерном массиве, а затем уже говорить про операции.
0
"Линейно-квадратичный регулятор" — к сожалению, это заимствованный термин, вытеснивший наш родной, русский. ТОУ ведь во многим обязана русским ученым, таким как Л.С. Понтрягин.
В русской школе ТОУ эта штука называлась "Аналитическое конструирование регуляторов".
Ну а если на пальцах — то упомянутый регулятор — это по сути тот же ПИД, но только с оптимально рассчитанными коэффициентами. Ну и немного в более общем виде — это такой регулятор, выходные функции которого являются линейной комбинацией переменных состояния, и метод их конструирования в сущности занимается расчетом коэффициентов этой линейной комбинации. В одномерном случае u=k*(x-x0), где u — управляющее воздействие, k — неизвестный коэффициент, x — измеряемая переменная состояния, x0 — ее желаемое значение.
В русской школе ТОУ эта штука называлась "Аналитическое конструирование регуляторов".
Ну а если на пальцах — то упомянутый регулятор — это по сути тот же ПИД, но только с оптимально рассчитанными коэффициентами. Ну и немного в более общем виде — это такой регулятор, выходные функции которого являются линейной комбинацией переменных состояния, и метод их конструирования в сущности занимается расчетом коэффициентов этой линейной комбинации. В одномерном случае u=k*(x-x0), где u — управляющее воздействие, k — неизвестный коэффициент, x — измеряемая переменная состояния, x0 — ее желаемое значение.
0
Не совсем согласен про (только) пид, но большое спасибо за справку. Не обессудьте, про Понтрягина, конечно, слышал, но обучаюсь по англоязычной литературе, отсюда кальки.
0
Насчет сходства линейно-квадратичного регулятора и ПИД могу пояснить следующее.
Метод аналитического конструирования регуляторов применим к объектам управления, описываемым линейными дифурами вида:
X'(t) = AX(t) + BU(t), где:
X(t) — вектор переменных состояния объекта xi(t), где i=1..n
X'(t) — производная по времени вектора переменных состояния
U(t) — вектор управляющих воздействий ui(t), i=1..n
A,B — матрицы
Если теперь рассмотреть частный случай, такой, что x2(t)=x1'(t), x3(t)=x2'(t) ирассчитать для такого объекта линейно-квадратичный регулятор вида:
U(t) = C*(X(t)-X0), где X0 — вектор желаемых значений переменных состояния, C — матрица
то получится по сути ПИД-регулятор для этого объекта, у которого рассматривается лишь одна из переменных состояния x2(t), ведь x3(t) — ее производная по времени, а x1(t) — интеграл.
Т.е. ПИД-регулятор с оптимально рассчитанными коэффициентами — это частный случай линейно-квадратичного регулятора, и для систем вроде тех, что я рассмотрел, аналитическое конструирование регуляторов не даст более оптимального решения, чем ПИД.
Но не следует забывать, что регулятор — это система для стабилизации переменных состояния объекта, парирующая малые их отклонения от заданного значения. Если же требуется привести объект в состояние X0 из далекого от него исходного состояния X1 — то эта задача оптимально решается не только и не столько регулятором, сколько оптимальным программным управлением.
Метод аналитического конструирования регуляторов применим к объектам управления, описываемым линейными дифурами вида:
X'(t) = AX(t) + BU(t), где:
X(t) — вектор переменных состояния объекта xi(t), где i=1..n
X'(t) — производная по времени вектора переменных состояния
U(t) — вектор управляющих воздействий ui(t), i=1..n
A,B — матрицы
Если теперь рассмотреть частный случай, такой, что x2(t)=x1'(t), x3(t)=x2'(t) ирассчитать для такого объекта линейно-квадратичный регулятор вида:
U(t) = C*(X(t)-X0), где X0 — вектор желаемых значений переменных состояния, C — матрица
то получится по сути ПИД-регулятор для этого объекта, у которого рассматривается лишь одна из переменных состояния x2(t), ведь x3(t) — ее производная по времени, а x1(t) — интеграл.
Т.е. ПИД-регулятор с оптимально рассчитанными коэффициентами — это частный случай линейно-квадратичного регулятора, и для систем вроде тех, что я рассмотрел, аналитическое конструирование регуляторов не даст более оптимального решения, чем ПИД.
Но не следует забывать, что регулятор — это система для стабилизации переменных состояния объекта, парирующая малые их отклонения от заданного значения. Если же требуется привести объект в состояние X0 из далекого от него исходного состояния X1 — то эта задача оптимально решается не только и не столько регулятором, сколько оптимальным программным управлением.
+1
О, вот теперь согласен полностью. Спасибо за развёрнутый комментарий. Если что, то более подробный разговор о непосредственно LQR в следующей статье, которая уже опубликована.
0
Извините, но то, что Вы написали, мне кажется спорным. То, что для цепочки из трех интеграторов структура регулятора со статическими обратными связями внешне похожа на структуру ПИД регулятора по второму состоянию, это не значит, что такое совпадение стоит обобщать.
Я соглашусь, что для скалярного объекта второго порядка ЛКР структурно соответствует ПД регулятору, но трактовать состояние объекта как И-компоненту регулятора это такое лукавство с потенциальными граблями.
Классический ПИД и классический ЛКР это разные вещи.
Я соглашусь, что для скалярного объекта второго порядка ЛКР структурно соответствует ПД регулятору, но трактовать состояние объекта как И-компоненту регулятора это такое лукавство с потенциальными граблями.
Классический ПИД и классический ЛКР это разные вещи.
0
Почему же? Рассмотрим простой случай — массивное тело, подверженное возмущениям, задача регулятора — стабилизировать положение тела в начале координат. Регулятор может подействовать на тело силой. Имеем уравнения объекта:
x1'(t) = x2(t)
x2'(t) = u(t)
где x1 — координата, x2 — скорость, u(t) — управляющее воздействие (ускорение).
Регулятор стабилизирует обе переменные состояния, и ЛКР, рассчитанный для этой системы, будет ПИ-регулятором. И-компонента появляется в системе естественным образом.
Я согласен, что ЛКР — это более общая структура регулятора, чем ПИД. Но для некоторых объектов управления ЛКР является ПИД (или даже ПИ/ПД).
x1'(t) = x2(t)
x2'(t) = u(t)
где x1 — координата, x2 — скорость, u(t) — управляющее воздействие (ускорение).
Регулятор стабилизирует обе переменные состояния, и ЛКР, рассчитанный для этой системы, будет ПИ-регулятором. И-компонента появляется в системе естественным образом.
Я согласен, что ЛКР — это более общая структура регулятора, чем ПИД. Но для некоторых объектов управления ЛКР является ПИД (или даже ПИ/ПД).
0
Если я правильно понял Ваш пример, то закон управления вида u=-(k1x1+k2x2), полученный как ЛКР, даёт нам ПД регулятор по положению x1, точнее даже по ошибке положения. Я не вижу тут И составляющую.
массивное тело, подверженное возмущениямВот при реакции на возмущения как раз и будет сильное отличие. Ключевой момент — ПД и ЛКР не изменяют порядок системы. Интегральная составляющая же расширяет пространство состояний, что и позволяет, например, повысить астатизм системы. Впрочем, думаю, Вы это и так знаете.
+1
Хорошо, убедили. Не задумывался над этим до такой степени.
В то же время, ничто не мешает "дополнить" объект новым уравнением состояния, реализовав И-составляющую расчетно, и уже по дополненному объекту рассчитать ЛКР.
В то же время, ничто не мешает "дополнить" объект новым уравнением состояния, реализовав И-составляющую расчетно, и уже по дополненному объекту рассчитать ЛКР.
0
А можете ответить чуть более подробно на вопрос "Почему квадрат?". Всегда меня мучал. То есть вот, например, у нас расстояния от точек до прямой в метрах. Тогда мы минимизируем… квадратные метры! Казалось бы, при чём тут они?.. И ещё. Вот мерили мы положения точек в метрах. Расстояние, допустим, 1, норма тоже 1. Теперь меряем в миллиметрах. Расстояние стало 10^3, а норма уже 10^6! Это немного смущает. Или не стоит пытаться сравнивать расстояние и норму?
0
«Почему квадрат?»
Если брать просто функцию расстояния, это будет ломанная линия — расстояние уменьшается до точки Xmin, а потом с переломом начинает расти. В Этой точке функция не дифференцируется — это по сути ломанная, т.е. две отдельных прямых, заданных отдельно. Квадрат при переходе через точку минимума дифференцируется. Соответственно, можно найти производную и минимум.
Расстояние стало 10^3, а норма уже 10^6!
Так это будет так для всех точек, для которых мы определяем минимум. И обеих осей. Ничео не изменится, хоть в попугая меряй.
+2
Есть несколько причин. Во-первых в матстатистике можно показать что МНК дает наиболее оптимальную оценку когда требуется оценить некую величину в которую замешан шум обладающий свойствами часто встречающимися на практике. Во-вторых, изрядное число методов минимизации работают не напрямую с функциями а с их производными, а производная функционала МНК — это та самая исходная матрица. В частности минимизация квадратичной функции сводится к решению простого линейного уравнения, тогда как минимизация расстояния (нормы L1) — это огромная головная боль и сложная проблема
+1
Мы ищем не просто минимум нормы, а минимум квадрата нормы. Почему? Сама точка минимума совпадает, а квадрат даёт гладкую функцию (квадратичную функцию от агрументов (alpha,beta)), в то время как просто длина даёт функцию в виде конуса, недифференцируемую в точке минимума. Брр. Квадрат удобнее.
А почему не куб или там какая-нибудь четная степень?
Я объясненья почему квадрат не понял.
0
Лифшиц входит к Ландау. Говорит: «Беда, Лев Давидыч! Я только что целую тетрадку выкладок в трамвае потерял! Как теперь писать будем?» Ландау (беспечно): «Ничего, напишем, как всегда: „Отсюда очевидно...“».
Вообще замечаю авторы часто прячут под «очевидно» кучу скелетов в шкафу и непроработки материала ))
Вообще замечаю авторы часто прячут под «очевидно» кучу скелетов в шкафу и непроработки материала ))
+2
Все картинки умерли.
0

Здесь вычисления опущены или мы считаем в уме обратные матрицы?
0

Математика на пальцах: методы наименьших квадратов