Комментарии 68
Чёрт, сначала порешал, а только потом заметил, что:
прекрасных дам-программистов
+3
Я не дама-программист, но все равно с удовольствием потягаюсь с кем-нибудь.
Шаг первый — набросал простенькую программку в двадцать строк — получил 151 ответ даже без скобок и факториалов.
-2-0-1+6 == 3
-2-0+1+6 == 5
-2-0+1*6 == 4
-2-0**1+6 == 4
+2-0/1/6 == 2
+20/1+6 == 26
201/6 == 33.5
+2/01*6 == 12
и т.д. Кто даст больше?
Шаг первый — набросал простенькую программку в двадцать строк — получил 151 ответ даже без скобок и факториалов.
-2-0-1+6 == 3
-2-0+1+6 == 5
-2-0+1*6 == 4
-2-0**1+6 == 4
+2-0/1/6 == 2
+20/1+6 == 26
201/6 == 33.5
+2/01*6 == 12
и т.д. Кто даст больше?
+1
33.5 не проходит условия
-1
33.5 это число лежащее в пределах 1 — 100. В условии ничего не сказано про целые числа.
+6
любое число от 1 до 100
Как насчёт длины полукруга радиусом 1?
+1
Я, конечно, понимаю, что совсем всё, скорее всего, и не получится, но…
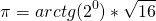
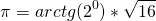
+12
Или, для любителей комплексных чисел,
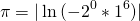
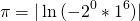
+14
можно использовать спец.символы :)
π = arctg(2°) * √16 — это можно скопировать мышкой 8)
просто к слову: пять лет назад я здесь на хабре написал, как сделал charmap.ru — онлайновую таблицу специальных символов :)
просто к слову: пять лет назад я здесь на хабре написал, как сделал charmap.ru — онлайновую таблицу специальных символов :)
+1
Всё очевидно не получится. Т.к. алфавит конечен, то формул не более чем счетно. А чисел континуум)
+4
del
-1
И вправду. Поэтому разумно потребовать в задаче найти все рациональные числа.
0
Это не доказательство, потому что вкладывать буквенные функции можно бесконечно много.
-1
11 как получилось?
0
Забавная задача, спасибо!
Для 11 можно так (2 + 0!)! -1 + 6
Для 11 можно так (2 + 0!)! -1 + 6
+2
Или так:
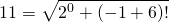
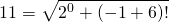
+1
Хм, а почему можно использовать степень 0.5 вне числа 2016?
Иначе голову ломать нечего — ясно, что для любого числа N > 0 всегда найдется x: (2016)^x = N.
Иначе голову ломать нечего — ясно, что для любого числа N > 0 всегда найдется x: (2016)^x = N.
+1
Потому что радикал можно использовать без явного указания степени. Я честно расставил только значки, не прибегая к цифрам. Задача-то на перебор на синтаксическом уровне, семантику не затрагивает. Есть унарная операция sqrt? Отлично, берём.
А если уж решать совсем в кругу программистов, то можно и до читерства с побитовыми операциями дойти. В постановке задачи, к сожалению, не прозвучал конкретный, исчерпывающий базис допустимых операций. В результате можно спорить о допустимости радикалов, о том, общепринято ли ~ в качестве bitwise not, и так далее.
А если уж решать совсем в кругу программистов, то можно и до читерства с побитовыми операциями дойти. В постановке задачи, к сожалению, не прозвучал конкретный, исчерпывающий базис допустимых операций. В результате можно спорить о допустимости радикалов, о том, общепринято ли ~ в качестве bitwise not, и так далее.
+3
Этим задачкам больше лет, чем мне. Раньше «Наука и Жизнь» их каждый год публиковала. Корень в этих задачах обычно использовать допускается. Равно как и целую часть. А вот условие «любое число от 1 до 100» как раз новое и странное: обычно требовалось порождать все целые числа по порядку и победителем становился тот, кто добирался до наибольшего числа. В обзорах обычно «каверзные числа» потом публиковались, на которых «застряли» большинство участников.
Понятно что появление мощных компьютеров свело ценность этой задачи к нулю. Как задачка для собеседования — она ещё годится, но на конкурс — уже нет. Где-то в начале XXI века конкурс прекратили…
Понятно что появление мощных компьютеров свело ценность этой задачи к нулю. Как задачка для собеседования — она ещё годится, но на конкурс — уже нет. Где-то в начале XXI века конкурс прекратили…
+3
2^0-1+6 == 6
2*0+1+6 == 7
2+0*1+6 == 8
2+0+1+6 == 9
2*(0+1)*6 == 12
-2+0+16 == 14
-(2^0)+16 == 15
2*0+16 == 16
2^0+16 == 17
2+0+16 == 18
(2*(0+1))^6 == 64
2*0+1+6 == 7
2+0*1+6 == 8
2+0+1+6 == 9
2*(0+1)*6 == 12
-2+0+16 == 14
-(2^0)+16 == 15
2*0+16 == 16
2^0+16 == 17
2+0+16 == 18
(2*(0+1))^6 == 64
0
-2+0-1+6=3
-2+0+1+6=5
2+0-1+6=7
2+0+1*6=8
2+0+1+6=9
20-1*6=14
20+1-6=15
20-1+6=25
20+1*6=26
20+1+6=27
В общем тут пару сотен чисел набрать можно.
-2+0+1+6=5
2+0-1+6=7
2+0+1*6=8
2+0+1+6=9
20-1*6=14
20+1-6=15
20-1+6=25
20+1*6=26
20+1+6=27
В общем тут пару сотен чисел набрать можно.
0
Я легко сделал 11
0
Без факториала 11 сделать невозможно.
0
Можно. Разрешается использовать операции x o b m
0
А кто это такие? xor, or и кто ещё?
0
Нашел еще решение для 11 практически на одних плюсах.
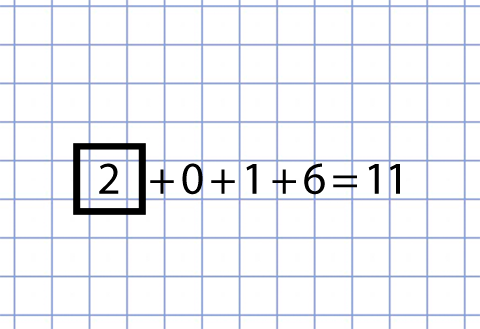
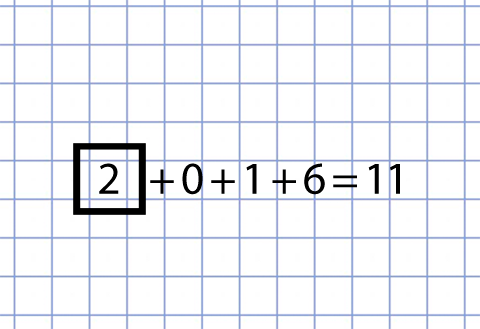
+4
Тогда я за строгую постановку задачи! =)
А то набросал скрипт на Питоне, для перебора всех не-читерских вариантов (скобки, базовые операторы, но без факториала). А там числа 11 нет.
И да, в новогоднюю ночь, в два часа ночи — кодить задачу, за которую даже не заплатят… Мне кажется, со мной что-то не так, доктор =) Всем хорошего Нового года!
А то набросал скрипт на Питоне, для перебора всех не-читерских вариантов (скобки, базовые операторы, но без факториала). А там числа 11 нет.
И да, в новогоднюю ночь, в два часа ночи — кодить задачу, за которую даже не заплатят… Мне кажется, со мной что-то не так, доктор =) Всем хорошего Нового года!
+3
А десятичная точка и периодическая дробь допускается? Например, .2^(0-1)+6?
0
Точка допускается, но в школьном варианте. То есть 0.2 легитимно. А Ваши программисткие Читы вне закона.
0
0.(1) считается школьным вариантом? 29=2+sqrt(sqrt(0.(1)^(-6)))
0
Периодическая дробь точно не допускалась (не помню точно почему), .2 не допускалось (всё-таки задачка родом из СССР, а не США), какие-то ещё ограничения были (чтобы пресечь «регулярные» решения, порождающие все числа формулами одинаковой структуры).
По-хорошему надо бы добраться до подшивки и посмотреть на оригинальную формулировку…
По-хорошему надо бы добраться до подшивки и посмотреть на оригинальную формулировку…
0
20-√16 = √16
-1
Для примера установим, что 01 = 1, 016 = 16. Берём операции + − * / fct (факториал) и pwr (возведение в степень) и полным перебором получаем ответы для 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 18, 19, 20, 21, 24, 25, 26, 27, 32, 36, 62, 64, 66, 100
Расширим операции до логических |^&~ и целочисленного деления (//). Получаем ответы для [0 — 81], [83 — 86], 89, 90, 95, 96, 99, 100.
Как видно, ближе к 100 начинаются проблемы, решаемые использованием других функций. Лично мне этот список функций неочевиден. Выше, например, используют sqrt. <sarcasm>Давайте зададим функцию, возвращающую порядковый номер перестановки чисел 2 0 1 6 с несколькими операторами</sarcasm>.
При проверке исключены варианты с большими степенями (дабы избежать out of memory при вычислении 20**(16!)), python-скрипт выложен на gist.
Ответы
0: (2 * (0 * (1 + 6)))
1: (2 + -(pwr(1, 6)))
2: (2 * (pwr(1, 6)))
3: (-(2 + 1) + 6)
4: (20 + (-16))
5: -(2 + -(1 + 6))
6: ((2 + (-1)) * 6)
7: (2 + ((-1) + 6))
8: (2 + (1 * 6))
9: (2 + (1 + 6))
10: (2 * ((-1) + 6))
12: (2 * (1 * 6))
13: (20 + -(1 + 6))
14: ((-2) + 16)
15: -(-(20 + 1) + 6)
16: (2 * (fct(0) + (1 + 6)))
18: (2 + 16)
19: (20 + -(pwr(1, 6)))
20: (20 * (pwr(1, 6)))
21: (20 + (pwr(1, 6)))
24: ((2 + (fct(0) + 1)) * 6)
25: (20 + ((-1) + 6))
26: (20 + (1 * 6))
27: (20 + (1 + 6))
32: (2 * 16)
36: (20 + 16)
62: -(2 + -(pwr((fct(0) + 1), 6)))
64: (pwr((2 * 1), 6))
66: (2 + (pwr((fct(0) + 1), 6)))
100: (20 * ((-1) + 6))
1: (2 + -(pwr(1, 6)))
2: (2 * (pwr(1, 6)))
3: (-(2 + 1) + 6)
4: (20 + (-16))
5: -(2 + -(1 + 6))
6: ((2 + (-1)) * 6)
7: (2 + ((-1) + 6))
8: (2 + (1 * 6))
9: (2 + (1 + 6))
10: (2 * ((-1) + 6))
12: (2 * (1 * 6))
13: (20 + -(1 + 6))
14: ((-2) + 16)
15: -(-(20 + 1) + 6)
16: (2 * (fct(0) + (1 + 6)))
18: (2 + 16)
19: (20 + -(pwr(1, 6)))
20: (20 * (pwr(1, 6)))
21: (20 + (pwr(1, 6)))
24: ((2 + (fct(0) + 1)) * 6)
25: (20 + ((-1) + 6))
26: (20 + (1 * 6))
27: (20 + (1 + 6))
32: (2 * 16)
36: (20 + 16)
62: -(2 + -(pwr((fct(0) + 1), 6)))
64: (pwr((2 * 1), 6))
66: (2 + (pwr((fct(0) + 1), 6)))
100: (20 * ((-1) + 6))
Расширим операции до логических |^&~ и целочисленного деления (//). Получаем ответы для [0 — 81], [83 — 86], 89, 90, 95, 96, 99, 100.
Ответы
0: (2 & 16)
1: (20 // 16)
2: (2 % 16)
3: (201 % 6)
4: (20 % 16)
5: ((2 + 1) ^ 6)
6: fct(201 % 6)
7: ((2 + 1) | 6)
8: (2 + (1 * 6))
9: (2 + (1 + 6))
10: (2 * ((-1) + 6))
11: ((~20) % 16)
12: ((-20) % 16)
13: ((~2) + 16)
14: ((-2) + 16)
15: -(2 + (~16))
16: (20 & 16)
17: -(2 | (~16))
18: (2 + 16)
19: -(2 ^ (~16))
20: (20 | 16)
21: (20 + (1 % 6))
22: ((20 * 1) | 6)
23: ((20 + 1) | 6)
24: fct(20 % 16)
25: (20 + ((-1) + 6))
26: (20 + (1 * 6))
27: ~(20 ^ (-16))
28: -(20 ^ (-16))
29: -(201 // (~6))
30: (20 | ((~1) * (~6)))
31: ~(2 * (-16))
32: (2 * 16)
33: (201 // 6)
34: -(2 * (~16))
35: ~((-20) + (-16))
36: (20 + 16)
37: -((-20) + (~16))
38: -((~20) + (~16))
39: ~(20 * ~(1 % 6))
40: -(20 * ~(1 % 6))
41: ~(fct(2 + 1) * (~6))
42: ((~20) * ~(1 % 6))
43: ~(20 + -(pwr((~1), 6)))
44: (20 + fct((~1) + 6))
45: (~(20 * (~1)) + 6)
46: (-(20 * (~1)) + 6)
47: ~((~2) * 16)
48: -((~2) * 16)
49: (~((~2) * (~1)) * (~6))
50: -(~((~20) * (~1)) + (~6))
51: ((~2) * (~16))
52: -(2 * ~(fct(0) + fct((~1) + 6)))
53: ~(~(20 // (~1)) * (-6))
54: (~(20 // (~1)) * 6)
55: ~(~(2 + fct(0)) * ((~1) * (~6)))
56: (~(fct(2 + fct(0)) + 1) * (~6))
57: ((~2) * ~(-((~0) + (~1)) * 6))
58: ~(fct(2 + fct(0)) + ~(pwr((~1), 6)))
59: ~((20 // (~1)) * 6)
60: -((20 // (~1)) * 6)
61: ~(2 + -(pwr((~1), 6)))
62: ~(2 + ~(pwr((~1), 6)))
63: -(2 + ~(pwr((~1), 6)))
64: (pwr((2 * 1), 6))
65: -(2 | ~(pwr((~1), 6)))
66: (2 + (pwr((~1), 6)))
67: -(2 ^ ~(pwr((~1), 6)))
68: -((~2) + ~(pwr((~1), 6)))
69: ~(-(20 // (~1)) * (~6))
70: ((20 // (~1)) * (~6))
71: ~((~2) * fct((~1) + 6))
72: -((~2) * fct((~1) + 6))
74: ~((~2) * -((~0) ^ fct((~1) + 6)))
75: ((~2) * ~(0 + fct((~1) + 6)))
76: ~(~(fct(2 + fct(0)) * (~1)) * (~6))
77: (~((-20) // (~1)) * (~6))
78: ((~2) * ~(fct(0) + fct((~1) + 6)))
79: ~(20 * -((~1) + 6))
80: (20 * ((~1) + 6))
81: (pwr((~2), ((~1) + 6)))
83: ~((~20) * ((~1) + 6))
84: (20 + (pwr((~1), 6)))
85: -(20 ^ ~(pwr((~1), 6)))
86: -((~20) + ~(pwr((~1), 6)))
89: ~(fct(2 + fct(0)) * ~((~1) * (~6)))
90: -(fct(2 + fct(0)) * ~((~1) * (~6)))
95: ~(~(2 + fct(0)) * fct((~1) + 6))
96: -(~(2 + fct(0)) * fct((~1) + 6))
99: ~(20 * (1 + (-6)))
100: (20 * ((-1) + 6))
1: (20 // 16)
2: (2 % 16)
3: (201 % 6)
4: (20 % 16)
5: ((2 + 1) ^ 6)
6: fct(201 % 6)
7: ((2 + 1) | 6)
8: (2 + (1 * 6))
9: (2 + (1 + 6))
10: (2 * ((-1) + 6))
11: ((~20) % 16)
12: ((-20) % 16)
13: ((~2) + 16)
14: ((-2) + 16)
15: -(2 + (~16))
16: (20 & 16)
17: -(2 | (~16))
18: (2 + 16)
19: -(2 ^ (~16))
20: (20 | 16)
21: (20 + (1 % 6))
22: ((20 * 1) | 6)
23: ((20 + 1) | 6)
24: fct(20 % 16)
25: (20 + ((-1) + 6))
26: (20 + (1 * 6))
27: ~(20 ^ (-16))
28: -(20 ^ (-16))
29: -(201 // (~6))
30: (20 | ((~1) * (~6)))
31: ~(2 * (-16))
32: (2 * 16)
33: (201 // 6)
34: -(2 * (~16))
35: ~((-20) + (-16))
36: (20 + 16)
37: -((-20) + (~16))
38: -((~20) + (~16))
39: ~(20 * ~(1 % 6))
40: -(20 * ~(1 % 6))
41: ~(fct(2 + 1) * (~6))
42: ((~20) * ~(1 % 6))
43: ~(20 + -(pwr((~1), 6)))
44: (20 + fct((~1) + 6))
45: (~(20 * (~1)) + 6)
46: (-(20 * (~1)) + 6)
47: ~((~2) * 16)
48: -((~2) * 16)
49: (~((~2) * (~1)) * (~6))
50: -(~((~20) * (~1)) + (~6))
51: ((~2) * (~16))
52: -(2 * ~(fct(0) + fct((~1) + 6)))
53: ~(~(20 // (~1)) * (-6))
54: (~(20 // (~1)) * 6)
55: ~(~(2 + fct(0)) * ((~1) * (~6)))
56: (~(fct(2 + fct(0)) + 1) * (~6))
57: ((~2) * ~(-((~0) + (~1)) * 6))
58: ~(fct(2 + fct(0)) + ~(pwr((~1), 6)))
59: ~((20 // (~1)) * 6)
60: -((20 // (~1)) * 6)
61: ~(2 + -(pwr((~1), 6)))
62: ~(2 + ~(pwr((~1), 6)))
63: -(2 + ~(pwr((~1), 6)))
64: (pwr((2 * 1), 6))
65: -(2 | ~(pwr((~1), 6)))
66: (2 + (pwr((~1), 6)))
67: -(2 ^ ~(pwr((~1), 6)))
68: -((~2) + ~(pwr((~1), 6)))
69: ~(-(20 // (~1)) * (~6))
70: ((20 // (~1)) * (~6))
71: ~((~2) * fct((~1) + 6))
72: -((~2) * fct((~1) + 6))
74: ~((~2) * -((~0) ^ fct((~1) + 6)))
75: ((~2) * ~(0 + fct((~1) + 6)))
76: ~(~(fct(2 + fct(0)) * (~1)) * (~6))
77: (~((-20) // (~1)) * (~6))
78: ((~2) * ~(fct(0) + fct((~1) + 6)))
79: ~(20 * -((~1) + 6))
80: (20 * ((~1) + 6))
81: (pwr((~2), ((~1) + 6)))
83: ~((~20) * ((~1) + 6))
84: (20 + (pwr((~1), 6)))
85: -(20 ^ ~(pwr((~1), 6)))
86: -((~20) + ~(pwr((~1), 6)))
89: ~(fct(2 + fct(0)) * ~((~1) * (~6)))
90: -(fct(2 + fct(0)) * ~((~1) * (~6)))
95: ~(~(2 + fct(0)) * fct((~1) + 6))
96: -(~(2 + fct(0)) * fct((~1) + 6))
99: ~(20 * (1 + (-6)))
100: (20 * ((-1) + 6))
Как видно, ближе к 100 начинаются проблемы, решаемые использованием других функций. Лично мне этот список функций неочевиден. Выше, например, используют sqrt. <sarcasm>Давайте зададим функцию, возвращающую порядковый номер перестановки чисел 2 0 1 6 с несколькими операторами</sarcasm>.
При проверке исключены варианты с большими степенями (дабы избежать out of memory при вычислении 20**(16!)), python-скрипт выложен на gist.
+2
В частности, 82 можно получить как -ceil(factorial((-2+0) * (~1)) / tan(6)), где tan возвращает тангенс в радианах. Сомнительное достижение.
0
sqrt отличается тем, что его можно общепринятым способом написать в линейной формуле, не используя букв и цифр — знаком радикала. Число сочетаний так уже не запишешь — придётся писать в два этажа, либо использовать букву C.
0
Вообще-то, раз уж вы разрешаете факториалы, могли бы получить 29 (и 27 по аналогии) как
29 = -20 + 1 + 6!!0
Двойного факториала, к сожалению, в списке нет. Как и других комбинаторных штучек.
0
Под «факториал», мне кажется, подходят двойные факториалы и субфакториалы.
0
С бинарными +, *, /, pwr(возведение в степень) и унарными -, fct (факториал), sfct (субфакториал), dfct (двойной факториал) получается ряд для [0 — 30], 32, 35, 36, 38, [41 — 57], [62 — 69], 72, 85, 88, 90, 92, [94 — 100].
Ответы
0: (2 * (0 * (1 + 6)))
1: dfct(2 + (-16))
2: (2 * (pwr(1, 6)))
3: (-(2 + 1) + 6)
4: (20 + (-16))
5: -(2 + -(1 + 6))
6: ((2 + (-1)) * 6)
7: (2 + ((-1) + 6))
8: (2 + (1 * 6))
9: (2 + (1 + 6))
10: (2 * ((-1) + 6))
11: (2 + sfct(-(fct(0) + 1) + 6))
12: (2 * (1 * 6))
13: (20 + -(1 + 6))
14: ((-2) + 16)
15: -(-(20 + 1) + 6)
16: (sfct(2) * 16)
17: (sfct(2) + 16)
18: (2 + 16)
19: (20 + -(pwr(1, 6)))
20: (20 * (pwr(1, 6)))
21: (20 + (pwr(1, 6)))
22: ((-2) + fct(-(fct(0) + 1) + 6))
24: fct(20 + (-16))
25: (20 + ((-1) + 6))
26: (20 + (1 * 6))
27: (20 + (1 + 6))
28: (-(20 * 1) + dfct(6))
29: -(20 + -(1 + dfct(6)))
30: (2 * dfct((-1) + 6))
32: (2 * 16)
35: (20 + dfct((-1) + 6))
36: (20 + 16)
38: (sfct(fct(2 + fct(0)) + (-1)) + (-6))
41: (-(2 + fct(0)) + sfct((-1) + 6))
42: ((-2) + sfct((-1) + 6))
43: (-(pwr(2, 0)) + sfct((-1) + 6))
44: sfct((-2) + (1 + 6))
45: (-(2 + 1) + dfct(6))
46: (-(2 * 1) + dfct(6))
47: -(2 + -(1 + dfct(6)))
48: dfct((2 + (-1)) * 6)
49: (2 + ((-1) + dfct(6)))
50: (2 + dfct(1 * 6))
51: (2 + (1 + dfct(6)))
52: (2 + (fct(0) + (1 + dfct(6))))
53: (fct(2 + fct(0)) + ((-1) + dfct(6)))
54: (fct(2 + 1) + dfct(6))
55: (fct(2 + fct(0)) + (1 + dfct(6)))
56: (dfct(2 + (fct(0) + 1)) + dfct(6))
57: (sfct(2 + (fct(0) + 1)) + dfct(6))
62: -(2 + -(pwr((fct(0) + 1), 6)))
63: -(sfct(2) + -(pwr((fct(0) + 1), 6)))
64: (pwr((2 * 1), 6))
65: (sfct(2) + (pwr((fct(0) + 1), 6)))
66: (2 + (pwr((fct(0) + 1), 6)))
67: (20 + ((-1) + dfct(6)))
68: (20 + dfct(1 * 6))
69: (20 + (1 + dfct(6)))
72: (fct(2 + (fct(0) + 1)) + dfct(6))
85: ((-20) + dfct(1 + 6))
88: (2 * sfct((-1) + 6))
90: (2 * (fct(0) + sfct((-1) + 6)))
92: (2 * (-(fct(0) + 1) + dfct(6)))
94: (2 * ((-1) + dfct(6)))
95: -(sfct(2) + -((fct(0) + 1) * dfct(6)))
96: (2 * dfct(1 * 6))
97: (sfct(2) + ((fct(0) + 1) * dfct(6)))
98: (2 * (1 + dfct(6)))
99: (dfct(fct(2 + fct(0)) + 1) + (-6))
100: (20 * ((-1) + 6))
1: dfct(2 + (-16))
2: (2 * (pwr(1, 6)))
3: (-(2 + 1) + 6)
4: (20 + (-16))
5: -(2 + -(1 + 6))
6: ((2 + (-1)) * 6)
7: (2 + ((-1) + 6))
8: (2 + (1 * 6))
9: (2 + (1 + 6))
10: (2 * ((-1) + 6))
11: (2 + sfct(-(fct(0) + 1) + 6))
12: (2 * (1 * 6))
13: (20 + -(1 + 6))
14: ((-2) + 16)
15: -(-(20 + 1) + 6)
16: (sfct(2) * 16)
17: (sfct(2) + 16)
18: (2 + 16)
19: (20 + -(pwr(1, 6)))
20: (20 * (pwr(1, 6)))
21: (20 + (pwr(1, 6)))
22: ((-2) + fct(-(fct(0) + 1) + 6))
24: fct(20 + (-16))
25: (20 + ((-1) + 6))
26: (20 + (1 * 6))
27: (20 + (1 + 6))
28: (-(20 * 1) + dfct(6))
29: -(20 + -(1 + dfct(6)))
30: (2 * dfct((-1) + 6))
32: (2 * 16)
35: (20 + dfct((-1) + 6))
36: (20 + 16)
38: (sfct(fct(2 + fct(0)) + (-1)) + (-6))
41: (-(2 + fct(0)) + sfct((-1) + 6))
42: ((-2) + sfct((-1) + 6))
43: (-(pwr(2, 0)) + sfct((-1) + 6))
44: sfct((-2) + (1 + 6))
45: (-(2 + 1) + dfct(6))
46: (-(2 * 1) + dfct(6))
47: -(2 + -(1 + dfct(6)))
48: dfct((2 + (-1)) * 6)
49: (2 + ((-1) + dfct(6)))
50: (2 + dfct(1 * 6))
51: (2 + (1 + dfct(6)))
52: (2 + (fct(0) + (1 + dfct(6))))
53: (fct(2 + fct(0)) + ((-1) + dfct(6)))
54: (fct(2 + 1) + dfct(6))
55: (fct(2 + fct(0)) + (1 + dfct(6)))
56: (dfct(2 + (fct(0) + 1)) + dfct(6))
57: (sfct(2 + (fct(0) + 1)) + dfct(6))
62: -(2 + -(pwr((fct(0) + 1), 6)))
63: -(sfct(2) + -(pwr((fct(0) + 1), 6)))
64: (pwr((2 * 1), 6))
65: (sfct(2) + (pwr((fct(0) + 1), 6)))
66: (2 + (pwr((fct(0) + 1), 6)))
67: (20 + ((-1) + dfct(6)))
68: (20 + dfct(1 * 6))
69: (20 + (1 + dfct(6)))
72: (fct(2 + (fct(0) + 1)) + dfct(6))
85: ((-20) + dfct(1 + 6))
88: (2 * sfct((-1) + 6))
90: (2 * (fct(0) + sfct((-1) + 6)))
92: (2 * (-(fct(0) + 1) + dfct(6)))
94: (2 * ((-1) + dfct(6)))
95: -(sfct(2) + -((fct(0) + 1) * dfct(6)))
96: (2 * dfct(1 * 6))
97: (sfct(2) + ((fct(0) + 1) * dfct(6)))
98: (2 * (1 + dfct(6)))
99: (dfct(fct(2 + fct(0)) + 1) + (-6))
100: (20 * ((-1) + 6))
+1
Если трактовать задачу как «записать числа от 0 до 200, используя в формулах только цифры 2, 0, 1, 6 в этом порядке и знаки препинания, в том числе с повторением», то можно выйти на любое целое число через «~-» и «-~». -~2016 = 2017, ~-2016 = 2015, ~-~-2016 = 2014 и т. д.
0
имхо 80 лаконичнее написать как 20*√16
0
С использованием x20 первой дыркой пока получилось 35.
0
а может в сторону универсальной формулы посмотреть?
если вдруг кто придумает как от второго логарифма избавиться…:
-log2(log2(0+√√√√√√...√√√√16))
где корень повторяется 3, 4, 5,… и т.д. раз для получения чисел 1, 2, 3,… соответственно
если вдруг кто придумает как от второго логарифма избавиться…:
-log2(log2(0+√√√√√√...√√√√16))
где корень повторяется 3, 4, 5,… и т.д. раз для получения чисел 1, 2, 3,… соответственно
+1
UPD:
-log2(ln(0+1^6*√√√√√√...√√√√e))
где корень повторяется 1, 2, 3, … и т.д. раз для получения чисел 1, 2, 3, … соответственно
путь, конечно, экстенсивный, да и цифры «0», «1», «6» — лишние,
но по формальным признакам — условию задачи соответствует
-log2(ln(0+1^6*√√√√√√...√√√√e))
где корень повторяется 1, 2, 3, … и т.д. раз для получения чисел 1, 2, 3, … соответственно
путь, конечно, экстенсивный, да и цифры «0», «1», «6» — лишние,
но по формальным признакам — условию задачи соответствует
+4
По формальным признакам оба варианта не подходят: в первом случае у вас задействована лишняя двойка, во втором — лишнее
e.0
Лишнее е – это не цифра. Буковки логарифма иначе тоже «лишние», и плохо въезжают в авторское «знаки и скобки». Если же проблема именно в константе – да пожалуйста:
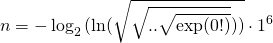
Не ошибся вроде?
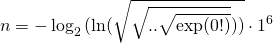
Не ошибся вроде?
+3
Ну, раз пошла такая пьянка – остаётся вспомнить про функцию sign и закрыть проблему. С её помощью двойка получается из любых двух первых цифр (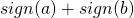 либо
либо 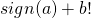 для
для  ).
).
Единица, нужная для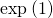 , получается из любых оставшихся цифр
, получается из любых оставшихся цифр 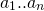 (как минимум две) перемножением
(как минимум две) перемножением  , если нулей нет, либо суммой двух произведений, в одном из которых нуль есть. Если остались одни нули – пользуемся тем, что 0! = 1.
, если нулей нет, либо суммой двух произведений, в одном из которых нуль есть. Если остались одни нули – пользуемся тем, что 0! = 1.
Теперь решение распространяется на решительно все последующие годы.
… фух…
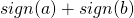 либо
либо 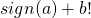 для
для 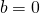 ).
). Единица, нужная для
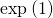 , получается из любых оставшихся цифр
, получается из любых оставшихся цифр  (как минимум две) перемножением
(как минимум две) перемножением 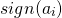 , если нулей нет, либо суммой двух произведений, в одном из которых нуль есть. Если остались одни нули – пользуемся тем, что 0! = 1.
, если нулей нет, либо суммой двух произведений, в одном из которых нуль есть. Если остались одни нули – пользуемся тем, что 0! = 1.Теперь решение распространяется на решительно все последующие годы.
… фух…
+2
Тогда можно попробовать так:
n/k = logln(√√√...√exp(20))(ln(√√√...√exp(16)))
Ведь логарифм по основанию, меньшему 1, не запрещён?
n/k = logln(√√√...√exp(20))(ln(√√√...√exp(16)))
Ведь логарифм по основанию, меньшему 1, не запрещён?
+2
Вовсе нет!
Вот и получилось решение для всех рациональных чисел. А если с сигнумами – так ещё и не зависящее от года, достаточно, чтобы цифр было более одной.
Да, кстати, множество алгебраических чисел же вроде тоже счётно?)
Вот и получилось решение для всех рациональных чисел. А если с сигнумами – так ещё и не зависящее от года, достаточно, чтобы цифр было более одной.
Да, кстати, множество алгебраических чисел же вроде тоже счётно?)
0
Ну если можно использовать функцию Эйлера, то 2=2 2=0!+1 2=phi(6) и готовы 2 двойки 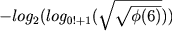
Если вдруг картинка не вставится, то вот ссылка
PS А может есть способ сделать из 0 и 1 шестёрку? Тоже сработает
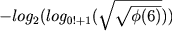
Если вдруг картинка не вставится, то вот ссылка
PS А может есть способ сделать из 0 и 1 шестёрку? Тоже сработает
0
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
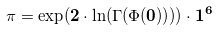
Задача про 2016