Комментарии 44
А всё-таки — чем крокодилы хуже? Точное решение найдено, по нему можно считать. При вычислениях на современной технике длина формул в этих пределах вроде бы не влияет ни на точность, ни на скорость. Какие ещё факторы?
+2
«Крокодилы» неудобны в дальнейших аналитических выкладках. В обеих задачах, где решалась приведенная система требовалось провести анализ, каковы должны быть a, b, A и B для того чтобы решение в принципе существовало. На практике это означало наличие условий на длины звеньев механизма (он может вырождаться и заклинивать), которые можно получить, анализируя решение по области определения функции arccos(x).
+6
К тому же, если Вы сравните сложность ответов в том и другом варианте решения задачи, Вы можете увидеть, что «вдумчивое» решение на порядок компактнее, а значит удобнее для дальнейшего использования
0
А вы пробовали упростить полученные «крокодилы» штатными функциями? В Mathematica, кажется, для этого есть Simplify и FullSimplify.
0
Simplify не дает желаемого эффекта. Упрощение путем применения стандартных функций, зачастую, производится с применением методик, принятых в данной СКА для решения задач данного класса. Чтобы СКА сделала так, как Вам надо, её необходимо об этом очень хорошо попросить. Пути для «свертки» сырого решения в СКА в полученную полуручным решением форму я не вижу
0
Попробуйте FullSimplify — он намного более общий (соответственно, и тормознутей на порядок)
0
Хотя, вот вариант применения Simplify к общему решению дает более компактную форму

Применение FullSimplify бросает нас в комплексную область

Но «ручками» с помошью СКА выходит всё равно проще и удобнее для анализа

Применение FullSimplify бросает нас в комплексную область

Но «ручками» с помошью СКА выходит всё равно проще и удобнее для анализа
+1
Согласен со статьёй. Аналогичные результаты с многоэтажными формулами получаются в Maple если проанализировать переходный процесс в колебательном контуре операторным методом. При этом Maple предполагает все коэффициенты комплексными и это приводит к формулам на весь экран. Чтобы этого не происходило ему нужно явно указывать тип всех коэффициентов real. После этого решение становится несколько компактнее.
Вобщем следует вывод, что компьютер не заменяет мозг. Даже если вы используется математические системы, это не отменяет необходимости думать над тем, что вы хотите получить от компьютера.
Вобщем следует вывод, что компьютер не заменяет мозг. Даже если вы используется математические системы, это не отменяет необходимости думать над тем, что вы хотите получить от компьютера.
+3
Чтобы не плодить крокодилов, нужно задавать «очевидные» вам условия. Ну, например, что A*A+B*B>0, что ab <> 0 и т.д. А то вы там лихо руками все соптимизировали, а компьютеру не разрешили.
Ну и FullSimplify наше все.
Ну и FullSimplify наше все.
+2
Я взял исходную задачу и быстренько решил на бумажке, места все выкладки вместе заняли существенно меньше чем выдача СКА.
Мое мнение — любое использование СКА в таких задачах вредно. Посмотрите — полученная дичайшая формула полностью скрывает физический смысл решения. Более того, использовать ее можно только одним способом — забить в ту же СКА и получать численный ответ для каждого набора параметров a, b, A, B. Таким образом, мы не только глубоко закопали «решение лежащее на поверхности», но и надежно спрятали его ото всех грядущих поколений, им остается только распечатать толстый «Справочник значений решения уравнения ...» и сверяться с ним при нужде.
Кстати, на думанье головой вместе с СКА, Вы кажется потратили больше усилий чем решая эту же задачу без него, так стоило ли вообще?
Проблема СКА в том что они предлагают легкий и быстрый путь, слишком соблазнительный для многих, однако при этом блокируют дальнейшее аналитическое исследование задачи.
Мое мнение — любое использование СКА в таких задачах вредно. Посмотрите — полученная дичайшая формула полностью скрывает физический смысл решения. Более того, использовать ее можно только одним способом — забить в ту же СКА и получать численный ответ для каждого набора параметров a, b, A, B. Таким образом, мы не только глубоко закопали «решение лежащее на поверхности», но и надежно спрятали его ото всех грядущих поколений, им остается только распечатать толстый «Справочник значений решения уравнения ...» и сверяться с ним при нужде.
Кстати, на думанье головой вместе с СКА, Вы кажется потратили больше усилий чем решая эту же задачу без него, так стоило ли вообще?
Проблема СКА в том что они предлагают легкий и быстрый путь, слишком соблазнительный для многих, однако при этом блокируют дальнейшее аналитическое исследование задачи.
0
1. Автор неопытен в использовании СКА, поэтому и затратил так много усилий. Любой инструмент нужно изучать, тем более такой сложный и альтернативно-умный.
2. Хорошо, когда начальная формулировка задачи красивая. Вот как у автора. В реальности у вас вполне могут быть «крокодилы» уже на входе. Потому что дана некая реальная фиговина, которая вот так, вот так, а потом вот так и в конце подвыверт. Крокодилов тоже руками будете преобразовывать?
3. Совершенно не обязательно сразу бабахать Solve. В большинстве случаев, если известен примерный план решения, проще преобразовывать вашу систему уравнений по шагам, оставляя СКА заниматься банальщиной. И при этом не бояться потерять где-нибудь минус.
4. Полученного крокодила можно выгрузить в виде функции на Си-подобном языке (по крайней мере в Mathematica). Что есть очень круто, если дальше нужно считать численно. Выгружаете в файл и дальше банально его include-те в нужном месте. Если что-то изменилось в формулах, пересчитываете файл nb, делаете новую выгрузку, а сишный код вообще не трогаете — всё подхватывается само. Дичайше удобно.
5. Ну и вообще, похоже на спор между копателем с лопатой и экскаваторщиком.
2. Хорошо, когда начальная формулировка задачи красивая. Вот как у автора. В реальности у вас вполне могут быть «крокодилы» уже на входе. Потому что дана некая реальная фиговина, которая вот так, вот так, а потом вот так и в конце подвыверт. Крокодилов тоже руками будете преобразовывать?
3. Совершенно не обязательно сразу бабахать Solve. В большинстве случаев, если известен примерный план решения, проще преобразовывать вашу систему уравнений по шагам, оставляя СКА заниматься банальщиной. И при этом не бояться потерять где-нибудь минус.
4. Полученного крокодила можно выгрузить в виде функции на Си-подобном языке (по крайней мере в Mathematica). Что есть очень круто, если дальше нужно считать численно. Выгружаете в файл и дальше банально его include-те в нужном месте. Если что-то изменилось в формулах, пересчитываете файл nb, делаете новую выгрузку, а сишный код вообще не трогаете — всё подхватывается само. Дичайше удобно.
5. Ну и вообще, похоже на спор между копателем с лопатой и экскаваторщиком.
+2
В общем согласен, да я и с автором тоже согласен более-менее.
Однако идея поста, как я ее понимаю, в том что аналитическое решение подразумевает дальнейший анализ, а доверяя машине мы получаем формально правильный ответ, но теряем возможность развития.
Однако идея поста, как я ее понимаю, в том что аналитическое решение подразумевает дальнейший анализ, а доверяя машине мы получаем формально правильный ответ, но теряем возможность развития.
Ну и вообще, похоже на спор между копателем с лопатой и экскаваторщикомТолько скорее между экскаваторщиком и археологом с совочком и кисточкой. У них просто цели ковыряния в земле разные.
0
В большинстве случаев, если известен примерный план решения, проще преобразовывать вашу систему уравнений по шагам, оставляя СКА заниматься банальщиной. И при этом не бояться потерять где-нибудь минус.
Так это и было проделано над рассмотренным примером
+1
А вот я считаю, что любой вывод формул (по крайней мере в физике) без использования СКА вообще недопустим. СКА даёт доказанный результат, в котором невозможно потерять какую-нибудь двойку или случайно поделить на ноль. В случае СКА можно оставлять реальную физическую структуру задачи, не делая уступок в упрощении записи.
Простой пример, найти собственные числа и вектора матрицы 2x2 довольно просто на бумажке, а вот 3x3 уже трудно, а 4x4 — нереально. И увидеть в ответе какую-то симметрию без использования СКА никак не выйдет, просто потому что ошибешься по 5 раз пока будет выписывать. А в СКА это делается за секунды.
СКА позволяет использовать аналитические методы там, где раньше использовали только численные. Насколько более ценной в физике является аналитическая формула, чем численная кривулина, объяснять даже излишне.
Простой пример, найти собственные числа и вектора матрицы 2x2 довольно просто на бумажке, а вот 3x3 уже трудно, а 4x4 — нереально. И увидеть в ответе какую-то симметрию без использования СКА никак не выйдет, просто потому что ошибешься по 5 раз пока будет выписывать. А в СКА это делается за секунды.
СКА позволяет использовать аналитические методы там, где раньше использовали только численные. Насколько более ценной в физике является аналитическая формула, чем численная кривулина, объяснять даже излишне.
+1
НЛО прилетело и опубликовало эту надпись здесь
Баги могут быть везде, тут уж ничего не поделать.
0
Иногда СКА дают не полный ответ (попробуйте решить переопределенную систему уравнений с неполиномиальными решениями), что в некоторых случаях хуже отсутствия ответа вообще, причем они делают это без предупреждения!
+1
del
0
Хорошо бы написать что такое четырёхзвенники, а то многие не в курсе.
С тригонометрией у СКА вообще беда, так что надо сразу преобразовывать к алгебраличесим уравнениям, а после решения поставлять обратно. А $Assumptions в Математике указывали? А то она ж, бедная, все считает комплексным по умолчанию. Ещё можно использовать всякие TrigExpand и прочие.
С тригонометрией у СКА вообще беда, так что надо сразу преобразовывать к алгебраличесим уравнениям, а после решения поставлять обратно. А $Assumptions в Математике указывали? А то она ж, бедная, все считает комплексным по умолчанию. Ещё можно использовать всякие TrigExpand и прочие.
0
А зачем нам теперь нужны классические методики преподавания математики (или физики, или механики) в школе или вузе.
В этом есть здравая мысль, но, это чревато деградацией. Школа — это базис, без него в вузе нечего делать, только в техникум. Некоторые сферы не будут существовать, если люди не будут знать, как решаются задачи руками, т.к. в голове не будет. значит, надо разделять школы по профилям, и вузы, где преподавать так, а где нет. А этот вопрос тоже спорный.
В этом есть здравая мысль, но, это чревато деградацией. Школа — это базис, без него в вузе нечего делать, только в техникум. Некоторые сферы не будут существовать, если люди не будут знать, как решаются задачи руками, т.к. в голове не будет. значит, надо разделять школы по профилям, и вузы, где преподавать так, а где нет. А этот вопрос тоже спорный.
+2
Так а всё равно без компьютера сейчас уже ничего не сделать, так что обучать им пользоваться, конечно нужно. То что ведет к деградации, я в корне не согласен, потому что компьютер убирает рутину, оставляя время для более интересных вещей. А кому не интересно, тому что с компьютером, что без компьютера не интересно.
0
Хорошая статья.
Считал я тут, давича, Гессиан для нейронной сети в общем случае. Причём вынужден был это делать почти что на бумажке. Вбивал в текстовой редактор, и перед началом каждого преобразования копировал выражение и менял его в копии. Так описок существенно меньше возникает, чем если реально на бумаге писать. Так вот заняло у меня это занятие три месяца в свободное от работы время.
Отсюда вопрос, а смогла бы СКА мне помочь если бы я умел ею пользоваться? Специфика задачи состоит в том, что нужно выражать производные одних значений через производные других при этом учитывая, что в некоторых случаях некоторые числа являются константами, а в некоторых других зависят от переменных по которым идёт дифференциирование.
Есть у СКА какие нибудь способы работать с такой мутью, не скажите случайно?
Считал я тут, давича, Гессиан для нейронной сети в общем случае. Причём вынужден был это делать почти что на бумажке. Вбивал в текстовой редактор, и перед началом каждого преобразования копировал выражение и менял его в копии. Так описок существенно меньше возникает, чем если реально на бумаге писать. Так вот заняло у меня это занятие три месяца в свободное от работы время.
Отсюда вопрос, а смогла бы СКА мне помочь если бы я умел ею пользоваться? Специфика задачи состоит в том, что нужно выражать производные одних значений через производные других при этом учитывая, что в некоторых случаях некоторые числа являются константами, а в некоторых других зависят от переменных по которым идёт дифференциирование.
Есть у СКА какие нибудь способы работать с такой мутью, не скажите случайно?
+1
НЛО прилетело и опубликовало эту надпись здесь
Как чем?! Регулярными выражениями! xkcd.ru/208
0
НЛО прилетело и опубликовало эту надпись здесь
При получении формул в математических пакетах не стоит рассматривать громоздкость как что-то плохое. Почти всегда это связано с рассмотрением огромного количества случаев, относительно параметров.
Возможно maisvendoo допустил какие-то ошибки при копировании полученных ответов, но полученный им ответ, к сожалению, неверен.
Я работаю на протяжении долгого времени в языке Wolfram Language (Mathematica), поэтому мне хотелось бы обратить внимание на следующее: известно что для такого рода задач используется функция Reduce, a не Solve.
Приведу ниже сравнение решений.
Красная точка — решение, полученное в Mathematica, синей точкой поверх нее пометилось бы решение, предложенное в статье.

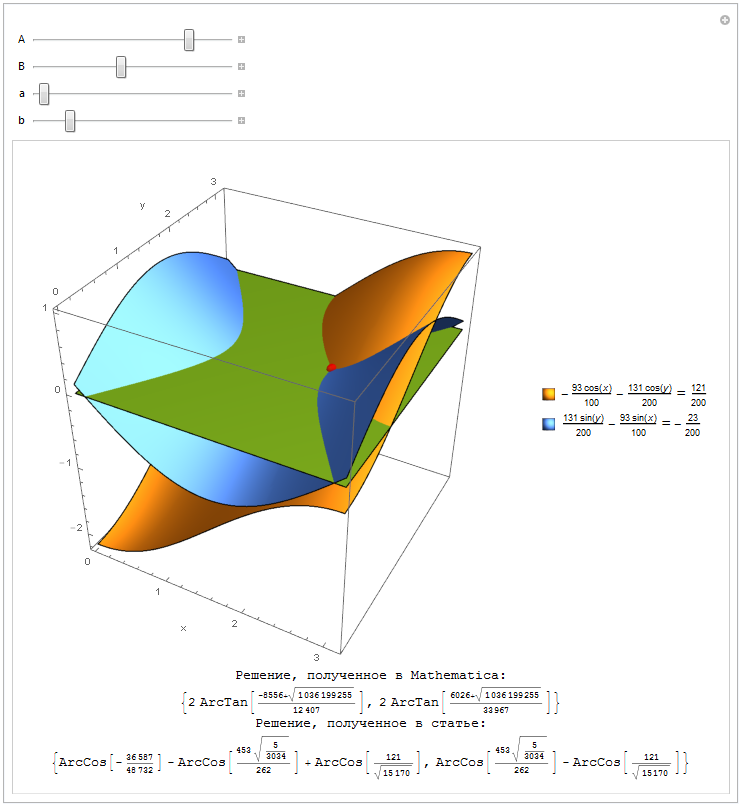
Возможно maisvendoo допустил какие-то ошибки при копировании полученных ответов, но полученный им ответ, к сожалению, неверен.
Я работаю на протяжении долгого времени в языке Wolfram Language (Mathematica), поэтому мне хотелось бы обратить внимание на следующее: известно что для такого рода задач используется функция Reduce, a не Solve.
Приведу ниже сравнение решений.
Красная точка — решение, полученное в Mathematica, синей точкой поверх нее пометилось бы решение, предложенное в статье.


Код для копирования
xVal[A_,B_,a_,b_]:=ArcCos[A/Sqrt[A^2+B^2]]-ArcCos[(A^2+B^2-a^2+b^2)/(2b Sqrt[A^2+B^2])]+ArcCos[(A^2+B^2-a^2-b^2)/(2a b)];
yVal[A_,B_,a_,b_]:=-ArcCos[A/Sqrt[A^2+B^2]]+ArcCos[(A^2+B^2-a^2+b^2)/(2b Sqrt[A^2+B^2])]
point[A_,B_,a_,b_,rhs_]:=Module[{x,y},{x,y}={xVal[A,B,a,b],yVal[A,B,a,b]};
If[Element[x,Complexes]||Element[y,Complexes],Graphics3D[],
Graphics3D[{Opacity[0.8],Blue,Sphere[{xVal[A,B,a,b],yVal[A,B,a,b],0},0.1]}]]]
mathematicaSolution[A_,B_,a_,b_]=Reduce[{a Cos[x]+b Cos[y]==A,a Sin[x]-b Sin[y]==B},{x,y}];
mathematicaSolutionPoints[A_,B_,a_,b_]:=Module[{solution},solution=ToRules@Quiet@Check[Reduce[{mathematicaSolution[A,B,a,b],0<x<Pi,0<y<Pi},{x,y},Reals],False];
If[solution=!=False,(mathematicaSolutionValue=FullSimplify[{x,y}/.solution]);Graphics3D[{Opacity[0.8],Red,Sphere[{x,y,0},0.06]}]/.solution,(mathematicaSolutionValue="Нет решений";Graphics3D[])]];
Manipulate[
{A,B,a,b}=Rationalize[{A,B,a,b}];
Grid[{{Show[{Plot3D[Evaluate@{a Cos[x]+b Cos[y]-A,a Sin[x]-b Sin[y]-B,0},{x,0,Pi},{y,0,Pi},ImageSize->500,PlotPoints->100,Mesh->False,BoxRatios->Automatic,AxesLabel->{"x","y",""},PlotLegends->{a Cos[x]+b Cos[y]==A,a Sin[x]-b Sin[y]==B}],point[A,B,a,b,A],mathematicaSolutionPoints[A,B,a,b]},SphericalRegion->True]},{"Решение, полученное в Mathematica:"},{mathematicaSolutionValue},{"Решение, полученное в статье:"},{{xVal[A,B,a,b],yVal[A,B,a,b]}}}],{{A,121/200},-1,1},{{B,-(23/200)},-1,1},{{a,-(93/100)},-1,1},{{b,-(131/200)},-1,1},TrackedSymbols:>{A,B,a,b}]+3
Возможно maisvendoo допустил какие-то ошибки при копировании полученных ответов, но полученный им ответ, к сожалению, неверен.
Я хотел бы уточнить у Вас, а в каком месте у меня ошибка?
0
Проверяйте все по шагам. Вы, скажем, выносите a за корень без модуля, что ошибка, если у вас параметр a может принимать отрицательные значения. Это первое, что в глаза бросилось. Я показал вам, что оно неверное, надеюсь вы сможете найти почему.
+1
Я выношу за корень, заранее зная, что углы не могут быть такими, что синус получится меньше нуля. Поэтому из под корня выносится положительное число
0
У вас 4 параметра. Ничто не мешает, вообще говоря, a быть отрицательным. Вы должны либо налагать ограничения на параметры, либо рассматривать все ситуации.
+1
параметры — положительны
0
Только что получил решение без СКА вручную
Получилось то же самое. Решение проверено мной многократно уже.
Был бы признателен, если бы мне указали на ошибку
Решение задачи из статьи



Получилось то же самое. Решение проверено мной многократно уже.
Был бы признателен, если бы мне указали на ошибку
0
Пардон, спутал знак, так что вторая картинка в посте выше выглядит так

Собственно ошибки здесь не вижу

Собственно ошибки здесь не вижу
0
Вот если вы говорите только о положительных параметрах, то ответ верен. Если параметры могут быть и отрицательны, то нет.
Это, вообще говоря, очень существенно и нужно было бы написать об этом в постановке задачи.
Это, вообще говоря, очень существенно и нужно было бы написать об этом в постановке задачи.
+1
Да, параметры положительны. При отрицательных величинах ход «ручного» решения другой. Внесу коррективу в статью, спасибо за полезное замечание.
P.S.: Функцию Reduce возьму на вооружение. Честно говоря, с Mathematica только начал знакомится, но по первым ощущениям она во многом затыкает Maple за пояс
P.S.: Функцию Reduce возьму на вооружение. Честно говоря, с Mathematica только начал знакомится, но по первым ощущениям она во многом затыкает Maple за пояс
0
Вы правы, Mathematica превосходит Maple практически во всем. Думаю, если поработаете плотнее, увидите это довольно быстро.
Если у вас возникнут вопросы по Mathematica, присоединяйтесь к сообществу Wolfram Mathematica® | Русскоязычная поддержка.
Если у вас возникнут вопросы по Mathematica, присоединяйтесь к сообществу Wolfram Mathematica® | Русскоязычная поддержка.
0
Mathematica превосходит Maple практически во всем
Я не стал бы судить категорично, но обратить внимание на Mathematica меня заставила такая задача
При получении уравнений Лагранжа 2-го рода приходится брать частную производную кинетической энергии по производной от обобщенной координаты и по самой обобщенной координате. А она в свою очередь — функция времени. При реализации этой задачи на Maple приходится вводить замену — ну не умеет он дифференцировать функцию по параметру, который сам является функцией. А Mathematica позволяет сделать вот так
LagrangeEQs[T_, q_, r_, F_]:= Module[{ret=Range[Length[q]]},
For[i = 1, i <= Length[q], i++,
ret[[i]] = D[D[T, D[q[[i]], t]], t] - D[T, q[[i]]] == Sum[F[[k]].D[r[[k]], q[[i]]], {k, 1, Length[F]}]
];
ret
]
тут T — выражение кинетической энергии; q — вектор обобщенных координат
и сразу получить аналитическое выражение уравнений движения в довольно компактном виде.
аналогичная функция в Maple выглядит так
LagrangeEQs := proc(T, q, r, F)
local s := numelems(q);
local n := numelems(rk);
local i, k;
local T1, dT1dv;
local dTdv, dTdvdt;
local T2, dT2dq;
local dTdq;
local left_part;
local Q;
local summa;
local r1, dr1dq, drdq;
# Получение левой части уравнений движения
for i from 1 to s do
# Дифференцируем кинетическую энергию по обобщенным скоростям и времени
T1[i] := subs(diff(q[i], t) = v[i], T);
dT1dv[i] := diff(T1[i], v[i]);
dTdv[i] := subs(v[i] = diff(q[i], t), dT1dv[i]);
dTdvdt[i] := diff(dTdv[i], t);
# Дифференцируем кинетическую энергию по обобщенным координатам
T2[i] := subs(q[i] = q1[i], T);
dT2dq[i] := diff(T2[i], q1[i]);
dTdq[i] := subs(q1[i] = q[i], dT2dq[i]);
# Формируем левую часть уравнения движения
left_part[i] := expand(simplify(dTdvdt[i] - dTdq[i]));
end do;
VectorCalculus[BasisFormat](false);
# Вычисляем обобщенные силы (правая часть уравнений движения)
for i from 1 to s do
summa := 0;
for k from 1 to n do
# Дифференцируем радиус-ректор точки приложения k-й силы по i-й обобщенной координате
r1[k] := subs(q[i] = q1[i], r[k]);
dr1dq[k] := VectorCalculus[diff](r1[k], q1[i]);
drdq[k] := subs(q1[i] = q[i], dr1dq[k]);
# Скалярно перемножаем вектор силы на производную от радиус-вектора по обобщенной координате
# и накапливаем результат
summa := summa + LinearAlgebra:-DotProduct(F[k], drdq[k], conjugate = false);
end do;
Q[i] := expand(simplify(summa));
end do;
# Окончательно формируем уравнения и возвращаем результатq
return {seq(left_part[i] = Q[i], i=1..s)};
end proc:
0
На самом деле вы использовали в Wolfram Language процедурную парадигму, которую желательно не использовать.
Используя функциональную парадигму, можно уменьшить код примерно в 2 раза. Если бы я знал детальное устройство вводимых параметров, то, думаю, можно было бы записать еще короче.
Используя функциональную парадигму, можно уменьшить код примерно в 2 раза. Если бы я знал детальное устройство вводимых параметров, то, думаю, можно было бы записать еще короче.
LagrangeEQs[T_,q_,r_,F_]:=
Table[D[D[T,D[q[[i]],t]],t]-D[T,q[[i]]]==Sum[F[[k]].D[r[[k]],q[[i]]],{k,1,Length[F]}],{i,1,Length[q]}]0
А тут случаем проблема не в том что какие-то банальные для человека граничные условия не были выражены в коде, и по этому СКА решает что-то гораздо более общее, по сравнению с тем что решается на бумажке?
0
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Системы компьютерной алгебры: блеск, нищета или почему многие задачи не решаются «в лоб»