Комментарии 25
Спасибо за статью!
А можно поподробнее про схему использованной сети? Я про «нестандартное расположение синапсов».
А можно поподробнее про схему использованной сети? Я про «нестандартное расположение синапсов».
+1
Сеть обычная не рекурентная, но на слои строго не разбита, синапс может идти к любому предыдущему нейрону. Накидано 460 синапсов из 630 комбинаторно возможных. Если ещё 170 докидать получится полносвязанная в самом брутальном смысле этого слова.
+1
Мне кажется рекуррентные сети куда более интересны, да и возможности у них потенциально больше.
т.е. в этом странность я не вижу. Конечно их редко используют на практике но вроде последние время о них было много публикаций (ИМХО).
т.е. в этом странность я не вижу. Конечно их редко используют на практике но вроде последние время о них было много публикаций (ИМХО).
0
Возможно если использовать разные функции активации можно получить еще более интересные результаты. Например добавить в часть нейронов синус и гаусса. Вот примеры картинок генерируемой сетью всего из 6 нейронов.
Входными данными являются координаты.


Входными данными являются координаты.


0
Класс! Как в мозг мне глядели!
Тоже хотел поэкспериментировать с таким, и сделать некоторые параметры функции активации, не связанные с синапсами также обучаемыми. Из моих чисто теоретических выкладок, связанных с понятием «удобной представимости» получается, что с некоторыми типами задач такие сети должны справляться сильно лучше при меньших размерах даже если примесный нейронов мало и они докинуты случайным образом.
Буду реализовывать эту идею где-то третьей-четвёртой в списке того, что хочу попробовать.
Тоже хотел поэкспериментировать с таким, и сделать некоторые параметры функции активации, не связанные с синапсами также обучаемыми. Из моих чисто теоретических выкладок, связанных с понятием «удобной представимости» получается, что с некоторыми типами задач такие сети должны справляться сильно лучше при меньших размерах даже если примесный нейронов мало и они докинуты случайным образом.
Буду реализовывать эту идею где-то третьей-четвёртой в списке того, что хочу попробовать.
0
Я не уверен что функции обязательно должны быть обучаемые. Может будет достаточно просто наличие таких в сети. По моей логике они облегчат формирование признаков генерируемых по этим законам. Пара — тройка синусов перед выходным слоем и хватит.
0
У меня на счёт удобства формирования признаков те же соображения. В одной из прошлых статей рассуждал на эту тему, правда на сильно вырожденном примере bias-а.
Обучаемые полезны для многих дел, но самое очевидное — период синуса. При функции активации Sin(SUM Wi) другие нейроны могут легко модифицировать сдвиг фазы, но периодичность могут менять только сложно с использованием ещё одного нейрона перед использующим синус. Если один обучаемый коэффициент уменьшает необходимую слойность сети на 1 это полезный коэффициент, IMHO.
Обучаемые полезны для многих дел, но самое очевидное — период синуса. При функции активации Sin(SUM Wi) другие нейроны могут легко модифицировать сдвиг фазы, но периодичность могут менять только сложно с использованием ещё одного нейрона перед использующим синус. Если один обучаемый коэффициент уменьшает необходимую слойность сети на 1 это полезный коэффициент, IMHO.
0
Интересно, получайте :) Все приведенные рассуждения справедливы для той модели, которую описывает автор. Но мозг работает совсем не так. То есть совсем совсем не так. Объяснить как в двух словах не получится слишком различаются архитектуры и парадигмы. Специалисты гугла правы и указанные ими моменты не устранимы в традиционной нейросетевой архитектуре. Понимаю, что без объяснения «а как на самом деле» ценность этого комментария не высока и прошу воспринимать его исключительно как мое частное мнение.
+4
Ну мнение меня и интересовало. Спаисбо :)
0
Как минимум мозг сильно сложнее. Одни только 4000 нейротрансмиттеров чего стоят. А вот наблюдаются ли в реальном мозге синаптические ансамбли или нет мы узнаем не скоро, потому что снимать потенциалы с синапсов уже научились, но это на порядок более трудозатратно, чем с нейронов. Да спайковая математика совсем иная нежели у формальных нейронов, но явление является следствием более фундаментальных свойств.
А специалисты гугла не правы и во второй части статьи тоже. Но чтобы объяснить подробно придется накатать ещё одну такого же размера статью. :) На той сети, которая описана в статье их «Лакун» практически нет. Малое изменение данных относительно правильных ведёт к резкому росту ошибки только на границах картинки, где сама учебная выборка очень не гладкая и выходит за рамки возможности сети.
То что они увидели — слабые обобщения. Я уже описывал в комментариях к статье TonyMas-а, но если и оформлю в виде отдельной статьи то не скоро.
А специалисты гугла не правы и во второй части статьи тоже. Но чтобы объяснить подробно придется накатать ещё одну такого же размера статью. :) На той сети, которая описана в статье их «Лакун» практически нет. Малое изменение данных относительно правильных ведёт к резкому росту ошибки только на границах картинки, где сама учебная выборка очень не гладкая и выходит за рамки возможности сети.
То что они увидели — слабые обобщения. Я уже описывал в комментариях к статье TonyMas-а, но если и оформлю в виде отдельной статьи то не скоро.
+3
Алексей, не пропадайте пожалуйста.
Ваши статьи очень интересны и многие заждались продолжения.
Также с радостью прочитаю вашу статью-ответ на эту на тему.
Ваши статьи очень интересны и многие заждались продолжения.
Также с радостью прочитаю вашу статью-ответ на эту на тему.
+3
Статья замечательная. Спасибо.
Вопрос следующий. Работу любого классификатора, в том числе и нейронной сети, можно объяснить в терминах разбиения пространства признаков ломанными линиями. В случае плоской картинки, классификатор должен, собственно, выделять области одного цвета. Что он и делает. Изменяя работу классификатора, мы меняем разбиение пространства ломанными, что и наблюдается в приведённых в статье анимациях.
Почему границы области примерно одного цвета названы синтаксическими признаками? Синтаксический признак, как я его понимаю, это раскрасить оба крыла в один цвет, выделив в в качестве признака — сигнатуру перьев. Тогда, такой признак будет изменять картинку симметрично. А в статье показаны отдельные ансамбли, изменяющие по отдельности правое и левое крылья. То есть — сеть не смогла найти общий признак и понять, что картинка на самом деле симметрична.
Вопрос следующий. Работу любого классификатора, в том числе и нейронной сети, можно объяснить в терминах разбиения пространства признаков ломанными линиями. В случае плоской картинки, классификатор должен, собственно, выделять области одного цвета. Что он и делает. Изменяя работу классификатора, мы меняем разбиение пространства ломанными, что и наблюдается в приведённых в статье анимациях.
Почему границы области примерно одного цвета названы синтаксическими признаками? Синтаксический признак, как я его понимаю, это раскрасить оба крыла в один цвет, выделив в в качестве признака — сигнатуру перьев. Тогда, такой признак будет изменять картинку симметрично. А в статье показаны отдельные ансамбли, изменяющие по отдельности правое и левое крылья. То есть — сеть не смогла найти общий признак и понять, что картинка на самом деле симметрична.
0
Ужас, кошмар какой. Не синтаксически, а семантически значимые, конечно же. Десять тысяч человек прочитало статью и вы первый, кто обратил внимание. Семантически значимый, тобишь кажущиеся людям осмысленными, имеющий некоторое знаковое значение для наблюдателя. Тоесть признаки введены наблюдателем по самому постороению.
На ваш вопрос не такой просто ответ. Дело в том, что сеть в процессе обучения стремится приблизиться к целевой функции, а это делать проще если удалось распутать признаки, однако это сети далеко не всегда удаётся. У меня, например, сеть не смогла понять, что картинка почти симметрична. Но очень часто выявление закономерностей и обобщений во входных данных проваливается с гораздо более страшным грохотом. В одной из предыдущих статей я рисовал картинку описанную во втором мысленном эксперименте этой статьи, когда сеть просят разделить точки над кривой и под кривой, но входные данные подаются в виде своих двоичных представлений. Сеть не справляется с придумыванием одной ломаной и начинает апроксимировать функцию множеством отдельных участков. Получается вот такой кошмар:
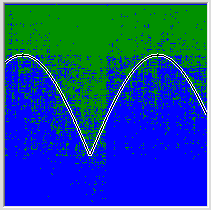
Ну тоже чему-то научилась, конечно.
Так вот то, удастся ли обнаружить компактный синаптический ансамбль как раз и зависит от того, удалось ли сети свойства входного сигнала распутать. Там где удалось ансамбли будут компактными, там где не удалось будет по одному ансамблю для каждого крыла. Или очень по-многу, как на этой картинке. Но сеть всё эе на до конца провалила тест. Есть группа синапсов которая синхронно управляет свойствами лопаток как одним целым.
Тоесть, с чем сеть справилась я показал, с чем сеть не справилась совершенно обосновано показали вы.
На ваш вопрос не такой просто ответ. Дело в том, что сеть в процессе обучения стремится приблизиться к целевой функции, а это делать проще если удалось распутать признаки, однако это сети далеко не всегда удаётся. У меня, например, сеть не смогла понять, что картинка почти симметрична. Но очень часто выявление закономерностей и обобщений во входных данных проваливается с гораздо более страшным грохотом. В одной из предыдущих статей я рисовал картинку описанную во втором мысленном эксперименте этой статьи, когда сеть просят разделить точки над кривой и под кривой, но входные данные подаются в виде своих двоичных представлений. Сеть не справляется с придумыванием одной ломаной и начинает апроксимировать функцию множеством отдельных участков. Получается вот такой кошмар:
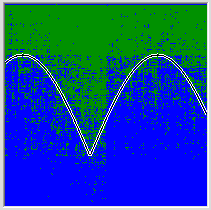
Ну тоже чему-то научилась, конечно.
Так вот то, удастся ли обнаружить компактный синаптический ансамбль как раз и зависит от того, удалось ли сети свойства входного сигнала распутать. Там где удалось ансамбли будут компактными, там где не удалось будет по одному ансамблю для каждого крыла. Или очень по-многу, как на этой картинке. Но сеть всё эе на до конца провалила тест. Есть группа синапсов которая синхронно управляет свойствами лопаток как одним целым.
Тоесть, с чем сеть справилась я показал, с чем сеть не справилась совершенно обосновано показали вы.
+1
Простите за некропостинг, но что не так с картинкой? по моему задача разделения синих и зеленых выполнена максимально разумно.
Чисто визуально количество синих точек выше линии примерно равно количеству зеленых точек ниже линии, при этом данная пропорция более-менее соблюдена не только в общей площади, но и по вертикальной оси.
Плохо что кривая слишком гладкая за счет большого количества частностей?
Так у сети много ресурсов (нейронов и связей), и она максимально ими пользуется для минимизации ошибки.
Уменьшим сеть, улучшим абстракцию за счет количества ошибок. Увеличим сеть — она нам по одному нейрону на точку съест, и ни одной ошибки не будет. Как впрочем и смысла в результате.
Или я не правильно понял что здесь неверно?
Чисто визуально количество синих точек выше линии примерно равно количеству зеленых точек ниже линии, при этом данная пропорция более-менее соблюдена не только в общей площади, но и по вертикальной оси.
Плохо что кривая слишком гладкая за счет большого количества частностей?
Так у сети много ресурсов (нейронов и связей), и она максимально ими пользуется для минимизации ошибки.
Уменьшим сеть, улучшим абстракцию за счет количества ошибок. Увеличим сеть — она нам по одному нейрону на точку съест, и ни одной ошибки не будет. Как впрочем и смысла в результате.
Или я не правильно понял что здесь неверно?
0
Некропостинг это хорошо, значит коммент не пропал даром. Смысл в данном случае вот в чём, во входных данных есть простая и чёткая закономерность. На вход подаются две координаты, в виде двух двоичных числ. В итоге получается 16 переменноых меняющихся строго [0,1]
Если бы сеть сумела сделать успешное обобщение чтобы хорошо замоделить задачу ей хватило бы 4 нейронов. Первый нейрон из двоичного входа складывал бы аналоговое число, по простейшему правило, второй делал бы то же самое для 8 других входов, а потом по одному нейрону на горб (сигмоида активации легко позволяет нарисовать горб одним нейроном). И ошибка была бы явно ниже, чем в данном случае. Вместо этого меть выучила прорву точек.
Вы правы, в части того что меньше-нейронов — больше обобщений. Проблема в том, что если вы оставите сети 4 нейрона, которые ей по идее только и нужны она всё равно нихрена не сумеет догадаться и обобщить, по крайней мере если будет руководствоваться Бэк-пропагейшеном. На самом деле если бы сеть хотя бы про два любых соседних входа догадалась, что их влияние отличается друг от друга строго в два раза она уже могла бы резко уменьшить ошибку. И тогда мы бы увидели на картинке некоторую регулярную структуру — вертикальные или горизонтальные полоски повторяющегося орнамента. Вы можете взять случайно созданную начальную сеть и весам каких-нибудь двух входов вручную установить нужное соотношение на синапсах хотя бы для части неронов первого слоя. И вы сразу увидите как улучшится найденный сетью вариант. Но на картинке регулярных полос нет — сеть оказалась беспомощной выявить эту закономерность.
Отсюда мой поинт — наращивание сейчас вычислительных мощностей даже постановка целой фермы GPU занятие довольно глупое пока ваш алгоритм не может справиться с на столько элементарной задачей. А когда у вас бует алгоритм, который такие вещи щёлкает то вам, возможно, и фермы GPU не понадобятся.
Если бы сеть сумела сделать успешное обобщение чтобы хорошо замоделить задачу ей хватило бы 4 нейронов. Первый нейрон из двоичного входа складывал бы аналоговое число, по простейшему правило, второй делал бы то же самое для 8 других входов, а потом по одному нейрону на горб (сигмоида активации легко позволяет нарисовать горб одним нейроном). И ошибка была бы явно ниже, чем в данном случае. Вместо этого меть выучила прорву точек.
Вы правы, в части того что меньше-нейронов — больше обобщений. Проблема в том, что если вы оставите сети 4 нейрона, которые ей по идее только и нужны она всё равно нихрена не сумеет догадаться и обобщить, по крайней мере если будет руководствоваться Бэк-пропагейшеном. На самом деле если бы сеть хотя бы про два любых соседних входа догадалась, что их влияние отличается друг от друга строго в два раза она уже могла бы резко уменьшить ошибку. И тогда мы бы увидели на картинке некоторую регулярную структуру — вертикальные или горизонтальные полоски повторяющегося орнамента. Вы можете взять случайно созданную начальную сеть и весам каких-нибудь двух входов вручную установить нужное соотношение на синапсах хотя бы для части неронов первого слоя. И вы сразу увидите как улучшится найденный сетью вариант. Но на картинке регулярных полос нет — сеть оказалась беспомощной выявить эту закономерность.
Отсюда мой поинт — наращивание сейчас вычислительных мощностей даже постановка целой фермы GPU занятие довольно глупое пока ваш алгоритм не может справиться с на столько элементарной задачей. А когда у вас бует алгоритм, который такие вещи щёлкает то вам, возможно, и фермы GPU не понадобятся.
0
Вы меня запутали с переходами между аналоговыми и цифровыми сигналами, так что я так и не понял что же должна была понять сеть (а ей сложнее, у нее меньше нейронов чем у меня). Но не суть. Общий смысл я уловил.
Конечно же использовать ровно столько нейронов сколько хватит теоретически это не самая удачная идея.
В любом случае существует некий «КПД».
А вообще примерно по этой причине я очень скептически отношусь к обратному распространению.
Нет, я понимаю что это решение имеющее хорошие практические результаты. Но у подобной архитектуры есть фундаментальные недостатки.
Вот вы упомянули «ферму GPU».
GPU это не Тру. Только ASIC, только хардкор.
Давайте представим себе сеть с учителем на ASICах, размером с первые компьютеры, т.е. занимающая несколько этажей.
Один вход — от микрофона. Один выход — динамик.
Ну ладно, даже на обоих концах сделаем предобработку, допустим Фурье, так что входов и выходов будет чуть побольше.
Ну не выйдет таким образом никакого Адама Селена. По крайней мере за время не больше времени существования Вселенной.
А вот у сетей без учителя это хоть и фантастика, но гораздо больше шансов.
Конечно глупо выходить даже за пределы CPU прежде чем твоя сетка научится сносно играть в Реверси (без учителя, обучаясь на игре сама с собой).
Но это верно для сферических сетей в вакууме стремящихся к сферическому ИИ.
Но к примеру в статье с которой я перешел на эту статью (вы указывали в комментариях) приводился пример того, что поиск близких по смыслу слов неработоспособен на маленьком корпусе. От слова совсем. А при большом корпусе и сеть нужна большая. В чисто практических задачах часто маленькие модели не заведутся.
Конечно же использовать ровно столько нейронов сколько хватит теоретически это не самая удачная идея.
В любом случае существует некий «КПД».
А вообще примерно по этой причине я очень скептически отношусь к обратному распространению.
Нет, я понимаю что это решение имеющее хорошие практические результаты. Но у подобной архитектуры есть фундаментальные недостатки.
Вот вы упомянули «ферму GPU».
GPU это не Тру. Только ASIC, только хардкор.
Давайте представим себе сеть с учителем на ASICах, размером с первые компьютеры, т.е. занимающая несколько этажей.
Один вход — от микрофона. Один выход — динамик.
Ну ладно, даже на обоих концах сделаем предобработку, допустим Фурье, так что входов и выходов будет чуть побольше.
Ну не выйдет таким образом никакого Адама Селена. По крайней мере за время не больше времени существования Вселенной.
А вот у сетей без учителя это хоть и фантастика, но гораздо больше шансов.
Конечно глупо выходить даже за пределы CPU прежде чем твоя сетка научится сносно играть в Реверси (без учителя, обучаясь на игре сама с собой).
Но это верно для сферических сетей в вакууме стремящихся к сферическому ИИ.
Но к примеру в статье с которой я перешел на эту статью (вы указывали в комментариях) приводился пример того, что поиск близких по смыслу слов неработоспособен на маленьком корпусе. От слова совсем. А при большом корпусе и сеть нужна большая. В чисто практических задачах часто маленькие модели не заведутся.
0
Я, извините, с критикой. Задорный эксперимент, будет как минимум полезным для дальнейших исследований. Но есть одна принципиальная ошибка.
Мозг человека в миллиарды раз сложнее анализируемой нейросети. Человеческий мозг настолько сложен, что в состоянии фантазировать, придумывать целые виртуальные миры, и стоить различного уровня правдоподобности гипотезы. Ему ничего не стоит «увидеть» в приведенных изменениях картинки какой-то определенный смысл, будь то наклон, цвет перьев, ширина туловища и т.п. критерии приведенные в статье.
Что, собственно, и произошло. Классификацию нейронов по назначению автор придумал (!) самостоятельно, рассматривая визуализацию возмущений отдельных нейронов и их вклад в общую визуализацию. Для некоторых нейронов ничего придумать не получилось. Вот если бы вы взяли 1000 разных птиц и всюду был бы найден отдельный нейрон или даже ансамбль, который отвечает за одну и ту же семантическую(!) характеристику, типа «это птица» «это не птица» тогда можно было бы о чем-то говорить.
Поэтому гугловцы — правы, т.к. их вывод статистически значим.
Мозг человека в миллиарды раз сложнее анализируемой нейросети. Человеческий мозг настолько сложен, что в состоянии фантазировать, придумывать целые виртуальные миры, и стоить различного уровня правдоподобности гипотезы. Ему ничего не стоит «увидеть» в приведенных изменениях картинки какой-то определенный смысл, будь то наклон, цвет перьев, ширина туловища и т.п. критерии приведенные в статье.
Что, собственно, и произошло. Классификацию нейронов по назначению автор придумал (!) самостоятельно, рассматривая визуализацию возмущений отдельных нейронов и их вклад в общую визуализацию. Для некоторых нейронов ничего придумать не получилось. Вот если бы вы взяли 1000 разных птиц и всюду был бы найден отдельный нейрон или даже ансамбль, который отвечает за одну и ту же семантическую(!) характеристику, типа «это птица» «это не птица» тогда можно было бы о чем-то говорить.
Поэтому гугловцы — правы, т.к. их вывод статистически значим.
+1
С одной стороны вы правы, придумать выделенным признакам названия было той самой иллюзией в голове наблюдателя, о которой писали гугловцы. Но дело в том, что распутывание кроме такого вот наблюдаемого смысла имеет ещё и строго математический, поддающийся измерению. Когда сеть успешно распутывает какие-нибудь признаки увеличивается количество особенностей изображения, которые она может запомнить, а синаптические ансамбли, кодирующие отдельные особенности становятся компактнее, включают меньшее количество синапсов и не пытаются разбить одно цветовое поле на несколько. Как результат это приводит также к улучшению качества апроксимации, доступной сети при найденых обобщениях. Это видно если по одной картинке обучить разные сети сильно много раз.

Например для вот этой сети, сумевшей распутать мнеьше признаков, как кажется тому самому мнительному наблюдателю внутри нас, порог ошибки в 0,235 оказался непробиваем, как ни играй параметрами обучения, а сеть приведённая в статье, и получившаяся более стимулирующей фантазию наблюдателя легко вытягивает 0.218.
А если бы я, как гугловцы, гонял тысячи изображений, или даже десятки тысяч, как гугловцы, а на выходе имел только классификацию «птицы — не птица», то я, точно так же как гугловцы, не мог бы посмотреть влияния на результат изменения одиночного синапса и об ансамблях и их компактности ничего бы не узнал.
Ещё немного подробностей есть в моём ответе предыдущему комментатору: habrahabr.ru/post/249031/#comment_8250053

Например для вот этой сети, сумевшей распутать мнеьше признаков, как кажется тому самому мнительному наблюдателю внутри нас, порог ошибки в 0,235 оказался непробиваем, как ни играй параметрами обучения, а сеть приведённая в статье, и получившаяся более стимулирующей фантазию наблюдателя легко вытягивает 0.218.
А если бы я, как гугловцы, гонял тысячи изображений, или даже десятки тысяч, как гугловцы, а на выходе имел только классификацию «птицы — не птица», то я, точно так же как гугловцы, не мог бы посмотреть влияния на результат изменения одиночного синапса и об ансамблях и их компактности ничего бы не узнал.
Ещё немного подробностей есть в моём ответе предыдущему комментатору: habrahabr.ru/post/249031/#comment_8250053
0
Не могу понять, почему сеть, натренированную на одной единственной картинке можно сравнивать с сетью, обученной на многих картинках.
Интуитивно кажется, что раз гугловцы, условно говоря, искали нейрон кошки, то есть многократно повторяющийся семантический признак во входных данных, то для единственной картинки следует искать что-то типа «нейрона часто встречаемых контурных участков».
Интуитивно кажется, что раз гугловцы, условно говоря, искали нейрон кошки, то есть многократно повторяющийся семантический признак во входных данных, то для единственной картинки следует искать что-то типа «нейрона часто встречаемых контурных участков».
0
>> Не могу понять, почему сеть, натренированную на одной единственной картинке можно сравнивать с сетью, обученной на многих картинках.
Потому что любое успешное обобщение это всего лишь нелинейное преобразование координат после которого задача классификации выглядит более решаемой. Задача может быть прямой классификацией (много разного на вход, простой выход), может быть классификацией вывернутой наизнанку, очень простые данные на вход, очень сложное ожидание на выходе. Сеть будет работать одинаково — искать такое нелинейное преобразование координат, после которого линейное разделение выглядит более понятным.
Поскольку речь шла о фундаментальных свойствах представления данных в сетях, а не о чём-то завязаном на входных данных, типа кластеризации, то вообще не важно по большому счёту как выглядит задачка, лишь бы сеть справилась с поиском обобщения. Пожтому я выбрал ту из возможных задач на которой тупо на глаз можно лучше понять происходящее в недрах сети.
Потому что любое успешное обобщение это всего лишь нелинейное преобразование координат после которого задача классификации выглядит более решаемой. Задача может быть прямой классификацией (много разного на вход, простой выход), может быть классификацией вывернутой наизнанку, очень простые данные на вход, очень сложное ожидание на выходе. Сеть будет работать одинаково — искать такое нелинейное преобразование координат, после которого линейное разделение выглядит более понятным.
Поскольку речь шла о фундаментальных свойствах представления данных в сетях, а не о чём-то завязаном на входных данных, типа кластеризации, то вообще не важно по большому счёту как выглядит задачка, лишь бы сеть справилась с поиском обобщения. Пожтому я выбрал ту из возможных задач на которой тупо на глаз можно лучше понять происходящее в недрах сети.
0
Понял, что меня смущает. Попробую сумбурно изложить.
Выше приводился аргумент, что в конечном итоге результат интепретируется человеком: «выход этого нейрона похож на кошку, а это — непонятная смесь, а это — поворот птицы».
Не будут ли из-за различий подходов предлагаться человеку принципиально разные «пятна Роршара»? В итоге, идеальный образ нейрона/ групп синапсов в одном случае хорошо согласуется с тем, что у людей в голове, а в другом — хуже.
Выше приводился аргумент, что в конечном итоге результат интепретируется человеком: «выход этого нейрона похож на кошку, а это — непонятная смесь, а это — поворот птицы».
Не будут ли из-за различий подходов предлагаться человеку принципиально разные «пятна Роршара»? В итоге, идеальный образ нейрона/ групп синапсов в одном случае хорошо согласуется с тем, что у людей в голове, а в другом — хуже.
0
Это чисто упрощение для меньших размеров статьи. Я же не говорю, что обобщения найденные сетью совпадают со значимыми для человека. Обобщения для сети это всего лишь преобразования, которые позволяют проще строить своё приближение к целевой функции.
А потому Можно автоматически выделять любое цветовое пятно, которое кажется человеку важным для построения, или даже просто любое большое, автоматически находить его границу, и соразмерять изменение ошибки связанное с изменением положения этой границы с изменением ошибки по всей тестовой выборке. Результат позволит полностью автоматизировать поиск ответственных за пятно синапсов, что само по себе интересно. Но никакой новой информации о способе кодирования внутри сети эта работа не даст. По крайней мере я думаю, что не даст. Если ошибаюсь, то упущу свою нобелевку.
А потому Можно автоматически выделять любое цветовое пятно, которое кажется человеку важным для построения, или даже просто любое большое, автоматически находить его границу, и соразмерять изменение ошибки связанное с изменением положения этой границы с изменением ошибки по всей тестовой выборке. Результат позволит полностью автоматизировать поиск ответственных за пятно синапсов, что само по себе интересно. Но никакой новой информации о способе кодирования внутри сети эта работа не даст. По крайней мере я думаю, что не даст. Если ошибаюсь, то упущу свою нобелевку.
0
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Ансамбль синапсов – структурная единица нейронной сети