Комментарии 102
Отличная работа. Что будет в части 2?
+2
Класс! Иногда кажется, что чёрные дыры реальны из-за нулей… поживём увидим!
-15
Сколько бы я ни читал различных популярных статей о том, почему на ноль делить нельзя, всё никак не мог понять, а, собственно, почему нельзя-то. Наконец автор данного замечательного труда донёс ту мысль, которая всегда не давала мне покоя — делить можно, просто получим другую алгебру с другими свойствами (я правильно всё понял?). Уффф… С нетерпением ждем продолжения!
+5
в первом приближении да — такие алгебры уже существуют. Выдумывать что-то свое уже не так заманчиво :)
+1
Как читатель, получивший диплом 10 лет назад и ни разу на практике теорию чисел (да и почти всего остального тоже) не применявший, я понял так, что:
1. В стандартных теориях введение исключений при делении на 0 позволяет избавиться от противоречий (и головняка) в свойствах поверх аксиоматики.
2. В данной статье описывается, как предки предложили специальные обозначения для двух типов сложных ситуаций, и в общем никто не запрещает эти случаи ещё раздробить – как обычно говорится в таких случаях, читателю предлагается проделать это самостоятельно [при желании].
1. В стандартных теориях введение исключений при делении на 0 позволяет избавиться от противоречий (и головняка) в свойствах поверх аксиоматики.
2. В данной статье описывается, как предки предложили специальные обозначения для двух типов сложных ситуаций, и в общем никто не запрещает эти случаи ещё раздробить – как обычно говорится в таких случаях, читателю предлагается проделать это самостоятельно [при желании].
0
- Строго говоря да. Формально 0 введен аксиомами Пеано. Об этом, в частности, во второй части
- Точно
+1
«Колеса» и «кольца», «поля» и «луга», я смотрю, у математиков своеобразное чувство юмора.
+2
Подозреваю, что школьный анекдот про «квадратный корень» и «многочлен» Вы тоже не слышали?
+3
Не слышал, но зато слышал про суперфакториал и суперпуперфакториал.
0
Озвучьте, если уж на то пошло.
+1
По типу такого?
5^2

+2
Про три вторых помните?:)
0
В JS это все реализовано в описанном виде, очень удобно.
-2
Что именно реализовано в JS в описанном виде?
+3
Получение Infinity и -Infinity при делении на ноль и их корректное поведение при дальнейших арифметических и логических операциях.
Например, Infinity * 0 дает NaN, что достаточно корректно отражает «не ноль» и т.п. в соответствии с описанной алгеброй.
Правда вторую неопределенность для 0/0 вводить не стали, ограничились NaN.
Например, Infinity * 0 дает NaN, что достаточно корректно отражает «не ноль» и т.п. в соответствии с описанной алгеброй.
Правда вторую неопределенность для 0/0 вводить не стали, ограничились NaN.
-2
Ах, это вы о IEEE 754. Смотрю, тут ниже уже ответили. Я добавлю, что все не так уж радужно, как кажется на первый взгляд. Например:
var a=0
for (var i=0; i<100; a+=0.1, ++i);
if (a != 10) console.log(«a = „+a+“ wtf?!»);
var a = 1e8, b = 1e-9;
if (a+b == a) console.log(a+"+"+b+" == " +(a+b)+ " wtf?!");
Второй пример в одинарной точности можно повторить, положив b = 1
Но это даже, не к IEEE 754 «претензии». Просто сетую на конечность битов и байтов %)
var a=0
for (var i=0; i<100; a+=0.1, ++i);
if (a != 10) console.log(«a = „+a+“ wtf?!»);
var a = 1e8, b = 1e-9;
if (a+b == a) console.log(a+"+"+b+" == " +(a+b)+ " wtf?!");
Второй пример в одинарной точности можно повторить, положив b = 1
Но это даже, не к IEEE 754 «претензии». Просто сетую на конечность битов и байтов %)
0
JS тут не причём, это IEEE 754. И в нём больше фич, чем вы думаете. И к математике он отношение имеет условное. Например, по нему 9e999==Infinity. :)
+3
Век живи)
0
Да уж. Cмесь понятий бесконечно малая и ноль выглядит весьма печально, с математической точки зрения.
console.log(-0)
// -0
console.log(0)
// 0
console.log(-0 === 0)
// true
console.log(-1/0)
// -Infinity
console.log(1/0)
// Infinity
0
Меня вот всегда интересовало почему математики не вводят, по аналогии с комплексными числами (i = sqrt(-1) ), значение еще одной мнимой единицы j = 1 / 0
-1
В расширенной комплексной плоскости уже много лет делят на ноль ))
+1
Полностью с Вами согласен. «Проективное расширение числовой прямой», рассмотренное в статье, частный случай «расширенной комплексной прямой». В статье, кстати, об этом говорится (есть ссылка на «Сферу Римана»).
0
По-моему сфера Римана несколько более естественна.
Насколько я помню универовский курс теории функций комплексного переменного, в случае комплексных чисел вокруг бесконечности можно даже в ряды разлагать.
Насколько я помню универовский курс теории функций комплексного переменного, в случае комплексных чисел вокруг бесконечности можно даже в ряды разлагать.
0
Вероятно именно поэтому на русскоязычной википедии есть много материала по расширенной комплексной плоскости, и практически ничего (на сегодня) по проективному расширению числовой прямой
0
Не нравится мне что беззнаковая бесконечность описывается тем же символом что и обычная. В частности, при умножении на -1 поведение становится неинтуитивным.
Я бы не плодил лишние абстракции и ограничения у традиционных сущностей — проще ввести отдельный знак или понятие.
Я бы не плодил лишние абстракции и ограничения у традиционных сущностей — проще ввести отдельный знак или понятие.
+2
удалено
0
А ноль на ноль делить можно? 0:0=0?
Если можно значит 2*0=0 и отсюда следует что 0:0=2. Заменим 2 на х, получается 0*х=0 и 0:0=х
Если можно значит 2*0=0 и отсюда следует что 0:0=2. Заменим 2 на х, получается 0*х=0 и 0:0=х
-11
Это же описано в топике в разделе про колеса:
Для начала попробуем разобраться со второй неопределенностью 0/0.
0
Лучше все таки прочитать статью. Там есть ответ на Ваш вопрос. Там есть пример изменения дистрибутивного закона, остальные тождества тоже весьма изменились.
+5
Дополним проективное расширение числовой прямой новым элементом, представляющим вторую неопределенность.
Если бы вы вместо этого написали перевод следующей цитаты, было бы намного понятнее.
Edalat and Potts [EP00, Pot98] suggested that two extra ‘numbers’, ∞ = 1/0 and ⊥ = 0/0, be adjoined to the set of real numbers (thus obtaining what in domain theory is called the ‘lifting’ of the real projective line) in order to make division always possible.
Carlström, Jesper: Wheels — on division by zero, 2001
0
А в чём, собственно, разница?
0
В принципе напомнить что привнесло «проективное расширение» имеет смысл. Дополнил. Холивар предлагаю вываливать в аналогичный комментарий чуть ниже. И на всякий случай напоминаю что в статье есть Disclaimer
0
В этом и дело, что в Disclaimer вы так и пишете
Вот в комментарии выше я про это и пишу, что в цитате на английском написано доступным «человеческим языком». Если бы вы также доступным языком написали — моего первого комментария и не было бы.
Цель данной статьи — объяснить «человеческим языком»
Вот в комментарии выше я про это и пишу, что в цитате на английском написано доступным «человеческим языком». Если бы вы также доступным языком написали — моего первого комментария и не было бы.
0
>2*0=0 и отсюда следует что 0:0=2
в рамках варианта статьи — не следует :)
в рамках варианта статьи — не следует :)
0
two extra ‘numbers’, ∞ = 1/0 and ⊥ = 0/0, be adjoined to the set of real numbers
Не просто обозначается, а вводится в набор чисел
0
Автор, огромное спасибо за стиль подачи материала. От человека, который думал, что перестал понимать математику окончательно и бесповоротно.
+3
Рад что труд полезен для Вас. Желание объяснить «на пальцах» — основная причина для выбора этого стиля подачи.
+2
Кстати, присоединяясь к благодарности выше, вторая благодарность за то, что кроме «на пальцах» вы все-таки оставляете немного «математического языка», что сильно помогает потом ковыряться в ссылках по теме.
И немного оффтопа — не посоветуете ли чего-нибудь на 100-200 страниц чтобы разобраться в основных современных математических теориях без страшенных формул, а то даже Википедию читать крайне сложно (там просто выдержки из вузовских учебников, непроходимых для людей со стороны). Или может сами сделаете серию статей-ликбеза по наиболее интересным вопросам?
И немного оффтопа — не посоветуете ли чего-нибудь на 100-200 страниц чтобы разобраться в основных современных математических теориях без страшенных формул, а то даже Википедию читать крайне сложно (там просто выдержки из вузовских учебников, непроходимых для людей со стороны). Или может сами сделаете серию статей-ликбеза по наиболее интересным вопросам?
+2
Самое доступное — англоязычная википедия (она намного шире русскоязычной в части математики). Доступная информация о «математике на пальцах», в моем случае, закончилась на производных (советская бумажная книга). Найти аналоги для «более высших материй» без страшных формул, к сожалению, больше везение.
Так что посоветовать Вам что-нибудь наподобие «вся вышка на пальцах» не могу.
Про статьи-ликбез. У меня есть заготовка по не евклидовым пространствам (где параллельные пересекаются). Но это уж точно не раньше второй части про деление на ноль.
Так что посоветовать Вам что-нибудь наподобие «вся вышка на пальцах» не могу.
Про статьи-ликбез. У меня есть заготовка по не евклидовым пространствам (где параллельные пересекаются). Но это уж точно не раньше второй части про деление на ноль.
+1
Роджер Пенроуз, «Путь к реальности или законы, управляющие вселенной». Первые ~300 страниц посвящены математике, начиная с обыкновенных дробей и аристотелевой логики и заканчивая тензорами, лагранжианами и алгеброй Ли.
На пальцах. Последовательно. Объясняя, как появился и зачем потребовался тот или иной математический аппарат.
На пальцах. Последовательно. Объясняя, как появился и зачем потребовался тот или иной математический аппарат.
0
Как раз недавно читал статью про деление на ноль с точки зрения полезности в языке программирования: www.jsoftware.com/papers/zero.htm. Там про то почему 0 / 0 = 0 может быть удобнее чем 0 / 0 = 1
0
На самом деле, есть ведь еще один аспект. Делить на ноль нельзя, потому что подобное деление не возникает при моделировании физической реальности, следовательно, вопрос «что будет, если поделить на ноль» абстрактен.
+1
Согласен с Вами. Бесконечность существует сама по себе (кое кто говорит что вселенная и время бесконечно :), независимо от математики, деления или нуля (сама по себе, так сказать).
0
мнимые числа в физической реальности встречаются что ли?)
+1
Волновая функция например.
0
физический смысл только у ее квадрата имеется )
речь же не про математические представления, а про реальный мир.
речь же не про математические представления, а про реальный мир.
0
Квантовая суперпозиция на мой взгляд — вопрос вполне себе физический.
0
тогда это философский вопрос из области «что считать реальным». фаза волновой функции реальна?
0
Вообще вся матемактика нереальна :-). Но некоторые математические выкладки позволяют предсказать поведение реальных предметов.
Так и с комплексными числами, и с волновой функцией. Хотя мне ближе пример с комплексной амплитудой и импедансом.
Так и с комплексными числами, и с волновой функцией. Хотя мне ближе пример с комплексной амплитудой и импедансом.
0
Я лично представляю мнимые числа просто как дополнительное измерение. В этом смысле они вполне могут встречаться в физической реальности.
0
А на мой взгляд, это костыль. То есть это же объективный факт, что они помогают решать реальные уравнения при этом самоустраняясь в ответах, и мне кажется, что это потому что мы пока упускаем какую-то часть математики, создающую такие эффекты
0
Это не костыль.
Математика, как и все другие точные науки, соответствует критерию Поппера и имеет (на сегодняшний взгляд) бесконечные перспективы развития.
Математика, как и все другие точные науки, соответствует критерию Поппера и имеет (на сегодняшний взгляд) бесконечные перспективы развития.
0
Ну, справедливости ради, математика критерию Поппера ни разу не соответствует, и наукой, в строгом смысле, не является. Математика — это язык моделирования реальности, позволяющий описать физическую теорию кратко и однозначно. Но, вообще говоря, никакая математическая теория ничем не хуже и не лучше любой другой и любая математическая абстракция (комплексные числа в том числе) имеет право на жизнь постольку, поскольку пригодна для моделирования. Даже противоречивые теории сами по себе ничем не плохи, просто они не имеют и не могут иметь приложений.
0
По-моему, скорее чисто вещественные числа — костыль) По крайней мере, читая хороший курс ТФКП, просто восхищаешься красотой и простотой предмета.
Кстати, отличная почти школьная книжка про комплексные числа: Арнольд, «Геометрия комплексных чисел, кватернионов и спинов»
Кстати, отличная почти школьная книжка про комплексные числа: Арнольд, «Геометрия комплексных чисел, кватернионов и спинов»
0
Это не костыль, это глобальное следствие неполноты любых формальных систем, в том числе и чисел.
Поэтому можно бесконечно расширять числа, и все эти дополнения не будут полны.
Поэтому можно бесконечно расширять числа, и все эти дополнения не будут полны.
0
А 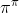 ?
?
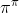 ?
?0
Для начала надо четко вывести число π, вот сразу после этого можно и поговорить )
0
Соотношение длины окружности круга к его диаметру.
UPD Длина полуокружности единичного радиуса, если придираться.
UPD Длина полуокружности единичного радиуса, если придираться.
0
>Соотношение длины окружности круга к его диаметру.
осталось лишь создать в физическом мире нечто, имеющее форму идеального круга )
осталось лишь создать в физическом мире нечто, имеющее форму идеального круга )
0
Ну тогда любая математическая абстракция не существует.
+1
Конечно, они лишь способ короче записывать что-то существующее. Например интеграл позволяет более кратко записать решаемую и без него задачу, и так почти со всей математикой. И с комплексными числами тоже.
0
Да. Они применяются, например, для описания колебаний и волн. Не только квантовых, еще и электрических. Я вам больше скажу: кватернионы — вполне себе реальные. Описывают вращение в трех измерениях.
0
Ох, если бы. Если признать ОТО и КМ полностью верными (читай, абсолютно точными) то вполне себе возникают. В частности, из-за этих самых делений на 0 провалилась теория струн а потом и суперструн.
0
А надо ли обязательно запихивать задницу и бесконечность на один уровень с остальными числами?
Вроде бы, если лифтануть арифметику в монаду Maybe, то получим алгебру, в которой задница (Nothing) будет честным идемпотентным множителем и слагаемым всего на свете, а Just 0 — идемпотентным множителем почти всего.
Если бы у нас ещё и бесконечность как-то была закодирована — например, если бы мы взяли Maybe Maybe Float, и на втором уровне Just Nothing символизировал бы бесконечность, — то мы получили бы проблему делителей нуля:
(Just Nothing) `lifted_mult` (Just Nothing) = Nothing.
А в ситуации с просто Maybe Float — всё хорошо.
Вроде бы, если лифтануть арифметику в монаду Maybe, то получим алгебру, в которой задница (Nothing) будет честным идемпотентным множителем и слагаемым всего на свете, а Just 0 — идемпотентным множителем почти всего.
Если бы у нас ещё и бесконечность как-то была закодирована — например, если бы мы взяли Maybe Maybe Float, и на втором уровне Just Nothing символизировал бы бесконечность, — то мы получили бы проблему делителей нуля:
(Just Nothing) `lifted_mult` (Just Nothing) = Nothing.
А в ситуации с просто Maybe Float — всё хорошо.
0
надо будет тщательнее вкурить в оригинал.
я-то говорю о том, что в поднятой алгебре… а, стоп-стоп… всё плохо. обычно идемпотент умножения это нейтраль сложения, что в арифметике, что в булевых алгебрах. а боттом — идемпотент обеих операций.
я-то говорю о том, что в поднятой алгебре… а, стоп-стоп… всё плохо. обычно идемпотент умножения это нейтраль сложения, что в арифметике, что в булевых алгебрах. а боттом — идемпотент обеих операций.
0
Ого, Вы добрались до понятия bottom :). Да, это идемпотент, но сам по себе (⊥*⊥=⊥+⊥=⊥). по отношению к другим элементам он «поглощает в себя все остальное» (⊥*5=⊥+5=⊥). А моноиды образованы по старинке, через нейтральные элементы 0 (сложение) и 1 (умножение) которые не оказывают влияние на исходный элемент.
0
Второй слой Maybe можно как бы и не делать — в Хаскеле уже есть ⊥, как допустимое значение почти всех идентификаторов.
Проблема в другом — полученная алгебра имеет взаимно-однозначное отображение на колесо. То есть, как бы красиво она не реализовывалась в Хаскеле, проблемы, присущие колесу, все равно останутся.
Проблема в другом — полученная алгебра имеет взаимно-однозначное отображение на колесо. То есть, как бы красиво она не реализовывалась в Хаскеле, проблемы, присущие колесу, все равно останутся.
+1
0
А я так ничего и не понял, троечник блин :'(
0
1)Сомневаюсь, что вводить обозначение «1\0 = бесконечность» удобно, лучше было бы что-то наподобие 1\0=S, потому что «2\0 + 1 = две бесконечности + 1» взрывает мозг, а 2\0 + 1 = 2S + 1 выглядит более удобно.
2)При прочтении статьи часто возникает ощущение, что под нулём вы подразумеваете не ноль, а нечто стремящееся к нулю в пределе, а это совершенно разные вещи.
3)Не увидел в статье примеров использования данного расширения, например можно было бы поискать решение системы уравнений: x*x=1 и y=1\(x-1); ответы: (1;S) (-1; -1\2).
4)В расширения поля 1\0=S возникает проблема с нейтральным элементом по сложению. 0 в качестве нейтрального уже не годится, т.к. как из следствие из ассоциативности, любой элемент * нейтральный по сложению = нейтральный по сложению, а в расширении S*0=1. Решение данной проблемы в статье я не увидел, поэтому нельзя говорить что поле расширения было построено.
2)При прочтении статьи часто возникает ощущение, что под нулём вы подразумеваете не ноль, а нечто стремящееся к нулю в пределе, а это совершенно разные вещи.
3)Не увидел в статье примеров использования данного расширения, например можно было бы поискать решение системы уравнений: x*x=1 и y=1\(x-1); ответы: (1;S) (-1; -1\2).
4)В расширения поля 1\0=S возникает проблема с нейтральным элементом по сложению. 0 в качестве нейтрального уже не годится, т.к. как из следствие из ассоциативности, любой элемент * нейтральный по сложению = нейтральный по сложению, а в расширении S*0=1. Решение данной проблемы в статье я не увидел, поэтому нельзя говорить что поле расширения было построено.
0
Пересмотрел статью и понял что вы и не собирались строить расширение поля, вы просто ввели элемент 1\0. В таком случае, от этого мало пользы: при решении уравнений нельзя использовать операцию минус (т.к. нет нейтрального по сложению и, как следствие, обратных). Если же каждое уравнение превращать в систему, вставляя проверку на то, не было ли деления на ноль (чтобы воспользоваться минусом), то непонятно зачем вообще было вводить это множество, т.к. получается такой же ход решения, как и над R. Получается что описанное вами множество а)не существует в нашем мире б)им нереально пользоваться, чтобы от него была какая-то польза, как от комплексных чисел.
0
Не очень понял про какое конкретно из расширений, представленных в статье, вы говорите. Отвечу предположив что вы про колеса.
Конечно вопрос применимости таких систем здесь не рассматривается. Статья существует лишь потому что люди упорно продолжают пытаться делить на ноль в нашей с Вами «реальности».
- Это сделано для упрощения восприятия далеких от темы людей (обсуждалось тут)
- Тут именно ноль. Все бесконечно малые были отброшены на проективном расширении
- Думаю в рамках «деления на ноль» понимания того «к чему мы пришли» достаточно на примере работы дистрибутивного закона. Иначе название статьи было бы Колеса и с чем их едят

- Про расширение поля, смотрю, Вы уже сами ответили. Дополню лишь что мы получили моноид по сложению и моноид по умножению. До группы такая система не дотягивает (есть нейтральные элементы, но нет есть обратных). Кстати все это описано в статье. По поводу уравнений см. п 3
Конечно вопрос применимости таких систем здесь не рассматривается. Статья существует лишь потому что люди упорно продолжают пытаться делить на ноль в нашей с Вами «реальности».
0
ОЙ, а тут похоже Уральский студент заявил о доказательстве жизни после смерти математической формулой из лимита 8/8 доказывают, что есть жизнь после смерти )))
0
Вторая часть готова Часть 2. Истина где-то рядом
0
Говорят, можно поделить на ноль если определить результат деления на ноль. Просто нужно расширить алгебру. По странному стечению обстоятельств найти хоть какой-то, а лучше понятный и простой, пример такого расширения не удается. Чтобы исправить интернет нужна либо демонстрация одного из способов такого расширения, либо описание почему это не возможно.
Как насчёт {0}?
Все операции определяются стандартно кроме того, что 0 является единицей по умножению.
Как следствие, 0/0 = 0, как и положено всякой уважающей себя единице.
+1
Получится 0*100500 = 100500. Думаю от такого расширения пользы маловато.
0
Мы же рассматриваем множество из одного 0, откуда там 100500, на который можно умножить?
Да и причём тут польза, просто пример, когда деление на 0 определено и обладает всеми основными свойствами ({0} получается полем).
Да и причём тут польза, просто пример, когда деление на 0 определено и обладает всеми основными свойствами ({0} получается полем).
+1
Я, сказать по правде, «множество из одного 0» даже как-то не ожидал :) Исходная идея в расширении школьной алгебры, без изменений существующих элементов.
А если по сути, Вы уверенны что это Поле, Операция сложения и умножения эквивалентны. То есть получается в алгебре определена всего одна операция. Группа — и то с натягом, если еще какую-нибуть аксиому не нарушит.
А если по сути, Вы уверенны что это Поле, Операция сложения и умножения эквивалентны. То есть получается в алгебре определена всего одна операция. Группа — и то с натягом, если еще какую-нибуть аксиому не нарушит.
0
Например, для пары двоек операции сложения, умножения, возведения в степень и дальнейших гиперумножений — эквивалентны :).
Операции определены по-разному, и мы с уверенностью говорим, что их две. Правда, в данном множестве они эквивалентны, да. Но их две.
Да, уверен. Обычно, определяя поле, также говорят о 9 аксиоме: неравенство нуля и единицы. Именно это вычёркивает {0} из разряда полей, и, кажется, из 9 аксиомы даже следует ряд разных хороших свойств.
Но делается это исключительно для удобства, чтобы не писать везде «выполняется везде, за исключением вырожденного поля».
Операции определены по-разному, и мы с уверенностью говорим, что их две. Правда, в данном множестве они эквивалентны, да. Но их две.
Да, уверен. Обычно, определяя поле, также говорят о 9 аксиоме: неравенство нуля и единицы. Именно это вычёркивает {0} из разряда полей, и, кажется, из 9 аксиомы даже следует ряд разных хороших свойств.
Но делается это исключительно для удобства, чтобы не писать везде «выполняется везде, за исключением вырожденного поля».
+1
Операции определены по-разному, и мы с уверенностью говорим, что их две. Правда, в данном множестве они эквивалентны, да. Но их две.
Хотя это интересный вопрос, конечно. Можно ли называть функции, определённые принципиально по-разному, но всегда дающие одинаковый результат (в рамках нашего «рабочего» множества), одинаковыми?
0
Наши рассуждения напомнили про «взляд 2-х мерных существ на 3-х мерные объекты». Думаю на множестве из одного элемента, невозможно дать разные определения функций. Попробуете, чисто из любопытства?
+1
Зарегистрируйтесь на Хабре, чтобы оставить комментарий


Делить на ноль — это норма. Часть 1