Комментарии 44
Шикарно. Давно не видел столь подробного раскладывания материала по полочкам, да еще и с картинками.
+3
Обстоятельно написано. А теперь можно еще и про кватернионы :)
+8
Так это ж аффинные преобразования. Там все матрицы есть: сдвига, поворота, растяжения/сжатия…
+6
Есть сомнения по поводу матрицы сдвига.
0
Вы правы. Но аффинное пространство по-хорошему строится «поверх» векторного. То есть векторное пространство надо объяснять так или иначе. Поворот—самую сложную из операций (как мне кажется)—можно объяснить сразу в векторном пространстве. После этого расширение до аффинного, переход к четырехмерным матрицам и все остальные матрицы (сдвиг, сжатие/растяжение, даже проекцию) понять очень просто. То есть такая последовательность изложения мне кажется оптимальной. Может быть, я когда-нибудь и напишу продолжение этой статьи.
0
Великолепно! Доходчиво и понятно. Продолжать в том же духе планируете?
+1
Спасибо! Вообще, я всего лишь хотел написать краткую заметку о том, почему некоторые звуки гармонируют, некоторые нет (на хабре было несколько статей, но они даже, можно сказать, с ошибками). Для этого нужно писать про преобразование Фурье. На хабре было несколько статей и про него, некоторые очень хорошие, но там нет того объяснения, которое мне нравится. А в этом объяснении используется матрица поворота. Поэтому пришлось писать вначале про матрицу поворота :-) Так что я планирую еще как минимум две статьи. И, может быть, по просьбам благодарных читателей про аффинные преобразования и кватернионы, если будет время.
0
Будем рады вашим новым статьям! Мне особенно было-бы интересно почитать про звуки. Так-же не будет лишней ещё одна статья про кватернионы в применении к трёхмерной графике (несмотря на обилие информации в своё время убил кучу времени чтобы «въехать» — очень мало информации излагается «на пальцах»).
+1
НЛО прилетело и опубликовало эту надпись здесь
У вас первая часть формулы (8) точно правильно написана? Она идентична (9).
+1
Разве преобразование позиции вершин происходит не по следующему алгоритму?
[экранная позиция вершины] = [vertex pos] * [world matrix] * [projection matrix] * [view matrix]?
Я что-то всерьёз сомневаюсь что в реальных приложениях действительно поворачивается базисный вектор в случае с поворотом.
А саму тему автор вообще даже и не раскрыл: собственно, вращение камеры в 3d-играх, оставив одни лишь домыслы и «матрица поворота из трёх других матриц поворота», что есть профанация, ибо сам поворот камеры задаётся в матрице проекции и собрать ещё можно одним шагом, без перемножения нескольких матриц.
Плюс, на эту тему был куда более информативный пост гораздо ранее: habrahabr.ru/post/126269/
[экранная позиция вершины] = [vertex pos] * [world matrix] * [projection matrix] * [view matrix]?
Я что-то всерьёз сомневаюсь что в реальных приложениях действительно поворачивается базисный вектор в случае с поворотом.
А саму тему автор вообще даже и не раскрыл: собственно, вращение камеры в 3d-играх, оставив одни лишь домыслы и «матрица поворота из трёх других матриц поворота», что есть профанация, ибо сам поворот камеры задаётся в матрице проекции и собрать ещё можно одним шагом, без перемножения нескольких матриц.
Плюс, на эту тему был куда более информативный пост гораздо ранее: habrahabr.ru/post/126269/
-1
> [экранная позиция вершины] = [vertex pos] * [world matrix] * [projection matrix] * [view matrix]
Тогда уж world * view * projection. Сначала вам надо внутримодельные координаты точки перенести в общемировые (с учетом того, где модель находится в мире) — это world (хотя чаще все-таки называют model). Потом необходимо сдвинуть / повернуть мир на необходимые расстояния и углы, чтобы камера оказалась в 0/0/0 — это view. Projection, наконец, спроецирует результат на воображаемый экран перед камерой определенным образом (перспективной проекцией, ортогональной, да как угодно).
Тогда уж world * view * projection. Сначала вам надо внутримодельные координаты точки перенести в общемировые (с учетом того, где модель находится в мире) — это world (хотя чаще все-таки называют model). Потом необходимо сдвинуть / повернуть мир на необходимые расстояния и углы, чтобы камера оказалась в 0/0/0 — это view. Projection, наконец, спроецирует результат на воображаемый экран перед камерой определенным образом (перспективной проекцией, ортогональной, да как угодно).
+1
Да, действительно, мог ошибиться с порядком. Несмотря на то, что произведение матриц некоммутативно, суть посыла осталась неизменна.
0
Со всем этим возюканьем не следует забывать, что этот набор матриц является не чем-то фундаментальным, а просто удобной абстракцией, принятой как стандарт.
В некоторых ситуациях матриц может быть меньше (например если модель изначально построена в координатах мира), или напротив больше (при использовании скелетной анимации). А некоторые операции с матрицами можно (и нужно) заменять операциями с кватернионами.
В некоторых ситуациях матриц может быть меньше (например если модель изначально построена в координатах мира), или напротив больше (при использовании скелетной анимации). А некоторые операции с матрицами можно (и нужно) заменять операциями с кватернионами.
+1
Да, само собой. Но этот набор является более-менее стандартным не в последнюю очередь потому, что эти три матрицы в нем получаются сами по себе простые. Ну то есть, например, ячейки матрицы view содержат в себе просто значения x, y, z и углов поворота, а не какие-нибудь адские формулы типа x*sin(a)+y*cos(b). Взял, закинул координаты и угол поворота камеры в матрицу, и всё. Это позволяет избежать лишних расчетов на стадии подготовки к рендеру кадра, оставив все подобные сложения и умножения на совести видеокарты, которая эти матрицы легко и эффективно пощелкает.
0
Попробую ответить по пунктам:
1. вершины в настоящей графике—объекты аффинного пространства, как справедливо заметили выше. И некоторые операции над вершинами присущи только ему. Но аффинное пространство строится «поверх» векторного, так что вначале стоит рассказать про векторное пространство
2. некоторые операции с вершинами и камерой не являются линейными операторами в векторном пространстве (сдвиг, например). То есть трехмерной матрицей их не задать. Но мы уже работаем в четырехмерном пространстве (чтоб разделять векторы и точки), а четырехмерными матрицами можно задать и сдвиг
3. Я не совсем понимаю, что вы имеете в виду под " в реальных приложениях… поворачивается базисный вектор в случае с поворотом". Поворот системы координат (для простоты будем говорить о 2D) на Х градусов против часовой стрелки эквивалентен повороту камеры на Х градусов по часовой стрелке. Который, в свою очередь, эквивалентен повороту наблюдаемых объектов на Х градусов снова против часовой стрелки. То есть формулы из статьи для поворота системы координат—такие же, как и для поворота камеры или объектов (только для камеры угол надо вставить в формулу со знаком минус).
3 а. Давайте посмотрим на пункт «2. Зачем компьютерной графике матрицы?» из ссылки из вашего комментария, на матрицу поворота:
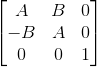 ,
,
Последний столбец и последняя строка проистекают из расширения векторного пространства до аффинного, их можно убрать. Коеффициенты А и B можно найти чуть выше в тексте: «Где A = sin(a), B = cos(a).» То есть оставшаяся двумерная матрица—как раз формула (12) из моей статьи. Собственно, основная цель моей статьи—дать общий вывод этой формулы.
4. Ваша ссылка замечательная, но у нее другой формат (как следует из названия), это FAQ. В нем формулы без определений, особого вывода и объяснения. Как я уже сказал, цель моей статьи—дать самые важные определения и вывод самой сложной и важной, на мой взгляд, формулы.
5. (боже, как много) поворот не задается в матрице проекции. Поворот объектов задается, как указали ниже, в матрице model, поворот камеры—во view. В проекции—только проекция (как следует и из вашего FAQ и собственно из названия матрицы).
6. "«матрица поворота из трёх других матриц поворота»… что есть профанация" Ссылка на википедию из последнего раздела сразу ведет на эти элементарные вращения, а следующий подраздел в статье на википедии—о том, как собрать из них общую матрицу поворота. И конечно, можно задавать вращения по-другому, о чем я и пишу в следующем абзаце.
7. если бы я описывал подробнее трехмерные вращения, статья была бы излишне большой. Мне кажется, если понять весь текст перед последним разделом, то ссылки на википедию понять очень легко. Это оптимальное решение, на мой взгляд.
Спасибо
1. вершины в настоящей графике—объекты аффинного пространства, как справедливо заметили выше. И некоторые операции над вершинами присущи только ему. Но аффинное пространство строится «поверх» векторного, так что вначале стоит рассказать про векторное пространство
2. некоторые операции с вершинами и камерой не являются линейными операторами в векторном пространстве (сдвиг, например). То есть трехмерной матрицей их не задать. Но мы уже работаем в четырехмерном пространстве (чтоб разделять векторы и точки), а четырехмерными матрицами можно задать и сдвиг
3. Я не совсем понимаю, что вы имеете в виду под " в реальных приложениях… поворачивается базисный вектор в случае с поворотом". Поворот системы координат (для простоты будем говорить о 2D) на Х градусов против часовой стрелки эквивалентен повороту камеры на Х градусов по часовой стрелке. Который, в свою очередь, эквивалентен повороту наблюдаемых объектов на Х градусов снова против часовой стрелки. То есть формулы из статьи для поворота системы координат—такие же, как и для поворота камеры или объектов (только для камеры угол надо вставить в формулу со знаком минус).
3 а. Давайте посмотрим на пункт «2. Зачем компьютерной графике матрицы?» из ссылки из вашего комментария, на матрицу поворота:
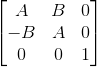 ,
,Последний столбец и последняя строка проистекают из расширения векторного пространства до аффинного, их можно убрать. Коеффициенты А и B можно найти чуть выше в тексте: «Где A = sin(a), B = cos(a).» То есть оставшаяся двумерная матрица—как раз формула (12) из моей статьи. Собственно, основная цель моей статьи—дать общий вывод этой формулы.
4. Ваша ссылка замечательная, но у нее другой формат (как следует из названия), это FAQ. В нем формулы без определений, особого вывода и объяснения. Как я уже сказал, цель моей статьи—дать самые важные определения и вывод самой сложной и важной, на мой взгляд, формулы.
5. (боже, как много) поворот не задается в матрице проекции. Поворот объектов задается, как указали ниже, в матрице model, поворот камеры—во view. В проекции—только проекция (как следует и из вашего FAQ и собственно из названия матрицы).
6. "«матрица поворота из трёх других матриц поворота»… что есть профанация" Ссылка на википедию из последнего раздела сразу ведет на эти элементарные вращения, а следующий подраздел в статье на википедии—о том, как собрать из них общую матрицу поворота. И конечно, можно задавать вращения по-другому, о чем я и пишу в следующем абзаце.
7. если бы я описывал подробнее трехмерные вращения, статья была бы излишне большой. Мне кажется, если понять весь текст перед последним разделом, то ссылки на википедию понять очень легко. Это оптимальное решение, на мой взгляд.
Спасибо
+1
Комментарий удален (промахнулся веткой).
0
Я все таки не понял откуда взялось 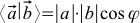 . Я помню ее со школы но почему она была скалярным произведением в школе было вовсе непонятно.
. Я помню ее со школы но почему она была скалярным произведением в школе было вовсе непонятно.
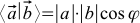 . Я помню ее со школы но почему она была скалярным произведением в школе было вовсе непонятно.
. Я помню ее со школы но почему она была скалярным произведением в школе было вовсе непонятно.0
Во-первых сперва показывается, что это величина инвариантная. Это значит, что если провести произвольный поворот системы координат, то она не изменится. В институте это является определением поворота ака ортогонального преоюразования; в школе же, кажется, это показывалось явно для двумерья (где можно тривиально записать матрицу поворота в общем виде — там только 1 параметр).
А во-вторых, если выбрать систему координат, в которой одну ось направить вдоль, скажем, вектора a, а вторую — так, чтобы оба вектора лежали в одной плоскости с обоими векторами, то тем самым координаты первого вектора будут (a, 0), а второго — (b cos \phi, b sin \phi); тем самым их скалярное произведение — то что нужно.
А во-вторых, если выбрать систему координат, в которой одну ось направить вдоль, скажем, вектора a, а вторую — так, чтобы оба вектора лежали в одной плоскости с обоими векторами, то тем самым координаты первого вектора будут (a, 0), а второго — (b cos \phi, b sin \phi); тем самым их скалярное произведение — то что нужно.
0
м… А если убрать косинус фи, просто оставить |a|*|b| то разве не будут те же инварианты сохраняться? Мой вопрос больше — откуда взялась эта формула. В чем смысл умножать длину вектора на длину проекции другого вектора на него?
0
НЛО прилетело и опубликовало эту надпись здесь
Я только такую циркуляцию знаю. 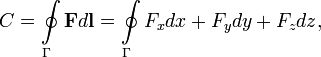

0
НЛО прилетело и опубликовало эту надпись здесь
ну блин. Это тяжело назвать определением скалярного произведения. Там просто пытаются найти элементарный вклад в векторную циркуляцию. Это проекция типа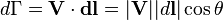 — например для гидродинамики.
— например для гидродинамики.
Но так определять веркторное произвидение мне кажется очень нелогичным и не отвечает на вопрос — откуда формула.
 — например для гидродинамики.
— например для гидродинамики.Но так определять веркторное произвидение мне кажется очень нелогичным и не отвечает на вопрос — откуда формула.
0
НЛО прилетело и опубликовало эту надпись здесь
Да, я тоже примерно так себе и представляю. Единственное, добавлю, что скалярное произведение в виде |a|*|b|, хоть, кажется, и удовлетворяет нужным аксиомам, но не очень удобно: нулевое значение его из векторов единичной длины (измеренных линейкой) не получить, то есть ортонормированный базис не построить.
0
Потому что изначально это было как ax*bx + ay*by + az*bz. Это — естественная вещь, много где проявляющаяся, и она является инвариантной.
0
Грубо говоря, скалярное поле образует правило (функция), которое каждой паре элементов ставит в соответствие число. Именно такая функция отлично подошла на эту роль для данного множества (эта функция удовлетворяет условиям скалярного произведения для данного множества).
0
Уж если про игры заговорили, то предупреждали бы неокрепшие умы о Gimbal Lock. Кватернионы не только решают эту проблему, но и легко интерполируются, позволяя описывать плавные анимации.
+7
Статья увлекательная, но вот название подкачало, теперь все ругаются словом кватернион =) Начнем с того, что статья не о камере и ее вращении, а о так называемых «афиновых преобразованиях» (перенос, масштаб, разворот или translate, scale, rotate) и о матричном представлении этих преобразований для трехмерного пространства с упором именно на поворот.
Управление камерой в 3D играх конечно же базируется на матричных преобразованиях, но так как все сводится к функции lookAt(eye, center, up) программисту достаточно поверхностного понимания всего описанного выше и все сводится к поиску вектора куда направлена камера, обычно это вектор движения возможно с вычитанием некоторого расстояние для того чтобы камера оказалась сзади, для стратегических игр можно добавить щепотку синусов и косинусов =) для вращения вокруг объекта.
Кватернионы о которых все говорят в комментариях конечно вещь полезная, но только по причине их безошибочной интерполяции (slerp) и в результате все сводится к тому, что углы поворота конвертируются в кватернион, затем его крутят и преобразуют в матрицу поворота на которую перемножают произведение матриц сдвига и масштаба.
Управление камерой в 3D играх конечно же базируется на матричных преобразованиях, но так как все сводится к функции lookAt(eye, center, up) программисту достаточно поверхностного понимания всего описанного выше и все сводится к поиску вектора куда направлена камера, обычно это вектор движения возможно с вычитанием некоторого расстояние для того чтобы камера оказалась сзади, для стратегических игр можно добавить щепотку синусов и косинусов =) для вращения вокруг объекта.
Кватернионы о которых все говорят в комментариях конечно вещь полезная, но только по причине их безошибочной интерполяции (slerp) и в результате все сводится к тому, что углы поворота конвертируются в кватернион, затем его крутят и преобразуют в матрицу поворота на которую перемножают произведение матриц сдвига и масштаба.
0
Насчёт «программисту достаточно поверхностного понимания» — не соглашусь. В применении к программисту трёхмерной графики это всё равно что сказать «Химику достаточно поверхностного понимания химии. Всё сводится к поиску нужных пропорций реагентов. Для сложных формул достаточно добавить щепотку учебника по химии для 8 класса».
+1
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Публикации
Изменить настройки темы
Как вращается камера в 3D играх или что такое матрица поворота