Комментарии 38
Спасибо, легко читается!
+2
Зря вы так про .NET. На Core i7 3.4 ГГц, 4 физических ядра (8 с HT):
Как видно, при минимуме кода, можно получить вполне эффективное распараллеливание вычислений.
Simple loop
Time: 00:00:07.6342930
Delta: -4,13447054370408E-13
ParallelEnumerable
Time: 00:00:01.8987034
Delta: -1,12732045920438E-12
Parallel.For
Time: 00:00:01.3737671
Delta: -3,9552361386086E-11
Parallel.ForEach
Time: 00:00:01.0942734
Delta: -9,59232693276135E-13
Как видно, при минимуме кода, можно получить вполне эффективное распараллеливание вычислений.
Код
using System;
using System.Collections.Concurrent;
using System.Diagnostics;
using System.Linq;
using System.Threading;
using System.Threading.Tasks;
namespace TempConsoleApplication {
public static class Program {
private const double Result = 1.2502304241756868163500362795713040947699040278200;
private const int IterCount = 200000000;
private static void Main(string[] args) {
Start("Simple loop", n => {
double sum = 0.0;
for (double i = 1.0; i <= n; ++i) {
sum += Math.Sin(i);
}
return sum;
});
Start("ParallelEnumerable",
n => ParallelEnumerable.Range(1, n).Select(i => Math.Sin(i)).Sum());
Start("Parallel.For", n => {
var sum = 0.0;
Parallel.For(
1,
n + 1,
() => 0.0,
(i, state, sumL) => Math.Sin(i) + sumL,
sumL => Sum(ref sum, sumL));
return sum;
});
Start("Parallel.ForEach", n => {
var sum = 0.0;
Parallel.ForEach(
Partitioner.Create(1, n + 1),
() => 0.0,
(range, state, sumL) => {
for (int i = range.Item1; i < range.Item2; ++i) {
sumL += Math.Sin(i);
}
return sumL;
},
sumL => Sum(ref sum, sumL));
return sum;
});
Console.ReadKey();
}
private static void Sum(ref double sum, double sumL) {
double initial, computed;
do {
initial = sum;
computed = initial + sumL;
}
while (initial != Interlocked.CompareExchange(ref sum, computed, initial));
}
private static void Start(string name, Func<int, double> func) {
func(100);
var s = Stopwatch.StartNew();
var sum = func(IterCount);
s.Stop();
Console.WriteLine(name);
Console.WriteLine("Time: " + s.Elapsed);
Console.WriteLine("Delta: " + (sum - Result));
Console.WriteLine();
}
}
}
+5
Спасибо, какой элегантный код. Раньше Net был очень небыстр, поэтому у меня были опасения. Но, конечно, в этом плане MS молодцы, допилили продукт ;-)
0
Библиотека TPL очень даже радует производительностью и удобством программирования. Я вот на ней недавно генетические алгоритмы обкатывал со сложной математикой.
А еще есть проект Accelerator, который имеет целью упрощение программирования GPGPU. До него руки не дошли пока.
А еще есть проект Accelerator, который имеет целью упрощение программирования GPGPU. До него руки не дошли пока.
0
НЛО прилетело и опубликовало эту надпись здесь
2x8 физических ядер с гипертредингом
Физических ядер всё-таки 8, а виртуальных 16.
0
Включение openmp (#pragma omp parallel for reduction (+: res)) + опция компилятора (/openmp) ускоряет C++-2012 c:
Result: 1.2502304241752471 after 8.642
до
Result: 1.2502304241745332 after 1.576
(взята медиана из 5 запусков).
Ускорение в 5.5 раз на Intel Core i7@2.8GHz
#pragma omp parallel for reduction (+ : res)
for (int i = 1; i <= 200000000; i++)
res+=sin(i);
Result: 1.2502304241752471 after 8.642
до
Result: 1.2502304241745332 after 1.576
(взята медиана из 5 запусков).
Ускорение в 5.5 раз на Intel Core i7@2.8GHz
0
Вот вам LabVIEW для коллекции с графиком скорости от ядер:
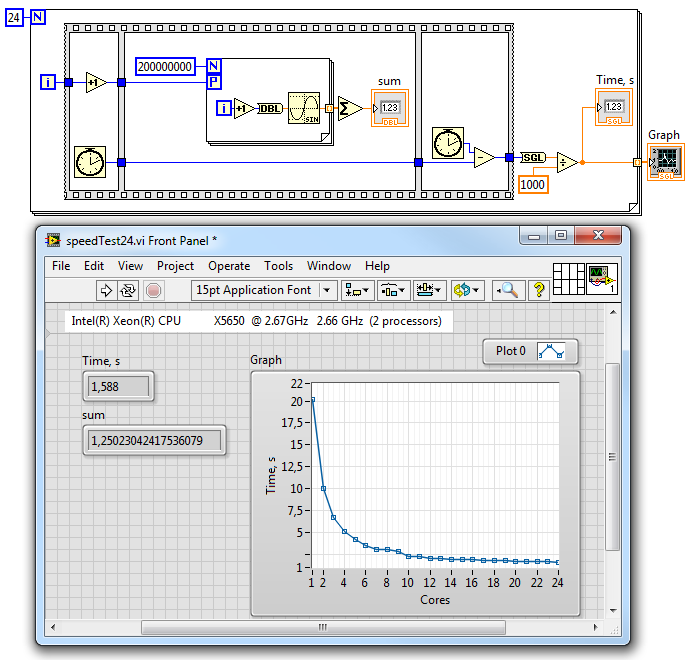
Чуть больше полутора секунд (но это 12 ядер с HT). Компилируется без проблем.

Чуть больше полутора секунд (но это 12 ядер с HT). Компилируется без проблем.
0
Раз уж пошла пьянка с .NET, вот вам еще пример (F#, Phenom II X6 1075T, 6 ядер по 3 ГГц)
let threadCount = 6
let serialSum first last =
let mutable res = 0.0
for i=first to last do
res <- res + sin(float i)
res
let parallelSum first last =
let count = last - first + 1
let perThreadCount = count / threadCount + (if count % threadCount = 0 then 0 else 1)
seq {
for i=0 to threadCount - 1 do
let localFirst = first + (perThreadCount * i)
let localLast = min last (localFirst + perThreadCount - 1)
yield async { return serialSum localFirst localLast }
}
|> Async.Parallel
|> Async.RunSynchronously
|> Array.sum
#time
> serialSum 1 200000000;;
Real: 00:00:06.930, CPU: 00:00:06.926, GC gen0: 0, gen1: 0, gen2: 0
val it : float = 1.250230424
> parallelSum 1 200000000;;
Real: 00:00:01.331, CPU: 00:00:07.644, GC gen0: 0, gen1: 0, gen2: 0
val it : float = 1.250230424
0
Зря вы так про интеловский компилятор. У меня 8 ядерный AMD. icpc version 13.1.1
icpc 200000000.c -o 200000000
Result: 1.250230424176175914
3.02 c (среднее по 5)
icpc 200000000.c -o 200000000 -parallel
0.626 c (среднее по 5) в 4.82 раза быстрее
правда результат скачет от
1.2502304241755670677 до
1.2502304241755675118
что конечно досадно, но это, пожалуй, отдельный разговор.
немного изменил код для Linux
icpc 200000000.c -o 200000000
Result: 1.250230424176175914
3.02 c (среднее по 5)
icpc 200000000.c -o 200000000 -parallel
0.626 c (среднее по 5) в 4.82 раза быстрее
правда результат скачет от
1.2502304241755670677 до
1.2502304241755675118
что конечно досадно, но это, пожалуй, отдельный разговор.
немного изменил код для Linux
смотреть исходник
#include <iostream>
#include <math.h>
#include <sys/time.h>
using namespace std;
unsigned long int time_delta(struct timeval *from, struct timeval *to) {
unsigned long int delta = to->tv_sec * 1000000l + to->tv_usec;
return delta - (from->tv_sec * 1000000l + from->tv_usec);
}
int main()
{
struct timeval start, end;
double res=0.0;
gettimeofday(&start, 0);
for (int i = 1; i <= 200000000; i++)
res+=sin(i);
gettimeofday(&end, 0);
cout.precision(20);
cout << "Result: " << res << " time: " << time_delta(&start, &end)/1000000.0 << "s" << endl;
}
0
3,02с. — это одним потоком? Проц разогнан? Думаю, если запустите мою VB-версию, результат будет лучше (только указывайте нужное число потоков).
my.rapidshare.com/fingoldo/9361
Если не опасаетесь запускать чужие экзешники )
my.rapidshare.com/fingoldo/9361
Если не опасаетесь запускать чужие экзешники )
0
Да, одним. Нет, не разогнан — 3.1 GHz FX-8120. Лень Wine устанавливать, удалять потом :-[
Лучше что-нибудь кросплатформенное.
Могу также сказать, что до 100'000'000, возможно cos(), на домашнем i5-760(тоже линукс) на JavaScript в Chrome 26-27 считалось за 4.2 с, в firefox 20 за 5.8 с. Как идея для добавления результатов.
Было бы очень удобно, если бы в конце статьи была табличка со всеми результатами.
Также недавно провёл пару тестов чтобы составить представление о том, как меняется результат вычисления от реализации численного метода. Результаты кода на ассемблере, gcc и icc хоть и незначительно, но отличались — 13 одинаковых знаков при всех промежуточных вычислениях в long double.
Лучше что-нибудь кросплатформенное.
Могу также сказать, что до 100'000'000, возможно cos(), на домашнем i5-760(тоже линукс) на JavaScript в Chrome 26-27 считалось за 4.2 с, в firefox 20 за 5.8 с. Как идея для добавления результатов.
Было бы очень удобно, если бы в конце статьи была табличка со всеми результатами.
Также недавно провёл пару тестов чтобы составить представление о том, как меняется результат вычисления от реализации численного метода. Результаты кода на ассемблере, gcc и icc хоть и незначительно, но отличались — 13 одинаковых знаков при всех промежуточных вычислениях в long double.
0
Тест очень синтетический, без комментариев.
По поводу GPU — всегда приходилось допиливать алгоритм под CUDA в сторону действительно массивной параллельности. Если на CPU у меня было, условно, 6 потоков по 10000 итераций, на GPU у меня было 10000 потоков по 100 итераций. Память в таком случае перестает волновать и быстрее было раз в 200 (по сути как теоретические гигафлопсы и говорят). Ну и double считать на них не надо совсем, скорость будет медленнее на порядок — учите математику, чтобы одинарной точности хватало.
По поводу GPU — всегда приходилось допиливать алгоритм под CUDA в сторону действительно массивной параллельности. Если на CPU у меня было, условно, 6 потоков по 10000 итераций, на GPU у меня было 10000 потоков по 100 итераций. Память в таком случае перестает волновать и быстрее было раз в 200 (по сути как теоретические гигафлопсы и говорят). Ну и double считать на них не надо совсем, скорость будет медленнее на порядок — учите математику, чтобы одинарной точности хватало.
0
Компилятор C++ не векторизовал ваш код. Он в принципе не может этого сделать. Векторизованные синусы считаются по другим формулам (и получаются менее точными) и их реализации в стандартной библиотеке разумеется нет. Если вы напишите векторизованный синус, то получите еще прирост скорости раза в 3.
+2
Векторизовал, SSE-вызовы в дизассемблере — тому доказательство. Да пусть бы менее точными, но быстрее )
-1
SSE-вызовы в дизассемблере доказывают то, что никакой векторизации нет. Как вы думаете сколько целочисленных значений загружает команда movd xmm0, esi в SSE регистр. Сколько прибавляет к счетчику цикла команда inc esi?
+3
Всё же он «векторизовал», хотя длина «вектора» и оказалась единичной, А вот почему так произошло и зачем такая «псевдовекторизация» нужна — вопрос разработчикам компилятора.
-1
Было бы еще интересно посмотреть на результат Wolfram Mathematica, её в этом наборе как-то не хватает.
0
Дорогу покажете? То есть, код подскажете? Я с этой системой никогда не работал.
0
За Mathematica не скажу, а вот Wolfram Alpha довольно резво считает:
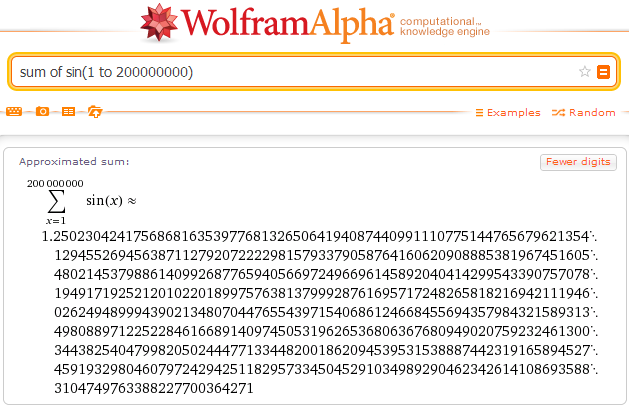
И тут же предлагает альтернативные формулы:

Эх, были бы такие инструменты лет пятнадцать-двадцать назад…

И тут же предлагает альтернативные формулы:

Эх, были бы такие инструменты лет пятнадцать-двадцать назад…
+1
In[1]:= Timing[NSum[Sin[i], {i, 1, 200000000}, WorkingPrecision -> 40]]Первое число в фигурных скобках — затраты машинного времени в секундах, второе — результат с точностью 40 знаков. Использован NSum[] — численное суммирование (стандартный Sum[] посчитает точное значение без округлений).
Out[1]= {0.358, 1.250230424175686816349232062751776829530}
Осторожно, честно производится только первое вычисление этого значения — все последующие, до перезагрузки мат. ядра, будут загружены из кэша, и затраты времени не будут связаны со скоростью вычислений.
Mathematica программируется куда более высокоуровнево, поэтому всех внутренних механизмов мне не понять. Очень вероятно, что сначала какими-то хитрыми способами сумма была посчитана символьно в общем случае для всех i, а потом единственное слагаемое вычислено для конкретного i=200000000. Вполне реалистичный путь, ведь символьно сумму он считает вообще очень быстро:
In[1]:= Timing[Sum[Sin[i], {i, 1, 200000000}]]
Out[1]= {0.046, 1/2 (Cot[1/2] — Cos[400000001/2] Csc[1/2])}
0
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Публикации
Изменить настройки темы

Выбор инструмента для расчётов с плавающей точкой — практические советы