Комментарии 37
Алгоритм работает на неориентированном графе единой стоимости.Неверно: у графа не бывает ни направлений, ни, тем более, диагоналей. Данный алгоритм работает на лабиринтах.
-15
Лолшто? Вот вам ориентированный граф, а что такое «лабиринт»? Всё то, что описывает статья может быть описано как граф, а препятствия — это переходы с бесконечно большим весом, вот и всё.
+11
По крайней мере не очень понятно, как согласуется выражение «единой стоимости» с тем фактом, что вес ортоганальных и диагоняльных переходов разный.
+3
Всё то, что описывает статья может быть описано как граф
Но не всякий граф может быть обработан алгоритмом Jump Point Search. Попробуйте найти естественных и принужденных соседей на вот этом фрагменте графа:
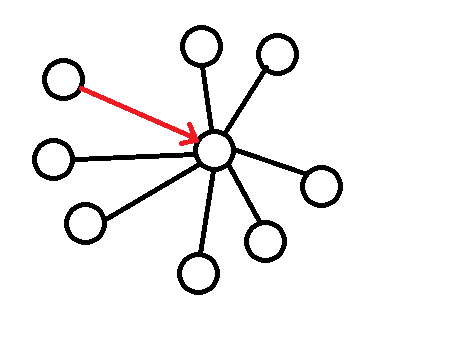
Алгоритм Jump Point Search применим к графам, порожденным регулярными структурами — например, раскрашенной квадратной сеткой. Только для квадратных сеток существуют такие понятия, как «прямой переход» и «диагональный переход». Только для сеток существует такое понятие, как координаты, которые активно используются функциями step и direction. Поэтому я и утверждаю, что понятие «граф» — слишком широкое для данной статьи.
PS С математической точки зрения, лабиринт — неориентированный граф, порожденный раскрашенной регулярной геометрической фигурой, при этом его вершины соответствуют внутренним областям фигуры, а ребра представляют собой отношения смежности областей.
Соглашусь с любым более точным определением, мне самому его объясняли «на пальцах».
+5
Спаибо за статью, интересная и много ссылок полезных для тех кто не вкурсе как оно там ищет пути. Кстати говоря, js реализация показывает разные роуты в зависимости от выбранного алгоритма, это означает что одни алгоритмы точнее других или же что существует несколько равнозначных путей?
+2
не заметил статистику зеленым внизу слева :) зачастую Jump Point Search быстрее чем Best First Search в два раза :) здорово!
0
роуты конечно разные, остальные алгоритмы не всегда находят лучший путь в итоге.
это алгоритм очень хорошо ищет и часто в разы меньше операций делает.
это алгоритм очень хорошо ищет и часто в разы меньше операций делает.
0
Вот что в разы быстрее я заметил, а что лучше ищет пока что не подобрал ситуацию при которой остальные алгоритмы выбирают не самый короткий путь. Если кто найдет повесте плиз скрин :) Любопытная штука эти алгоритмы поиска пути!
0
+5
а тогда сравнение некорректное, работающий алгоритм с медленным неработающим :)
0
почему некорректное то? и почему алгоритм не работающий?
путь найден, пусть и не самый оптимальный.
путь найден, пусть и не самый оптимальный.
+2
Потому что BFS не ищет оптимального пути вообще, он ищет любый.
Сравнивайте JPS с A*, они оба ищут оптимальные пути.
Сравнивайте JPS с A*, они оба ищут оптимальные пути.
0
Видимо, дело в том, что BFS вообще не умеет в классической реализации учитывать стоимость пути, а у нас здесь есть диагональные переходы, которые BFS может оценивать как 2 перехода стоимостью 1, либо 1 переход стоимостью 1. Нужно смотреть исходники.
0
Вот вам пример, хоть и разница не большая, но она есть
глянуть



0
Наглядный пример. Очень быстрый поиск. Надо попробовать
+1
Авторы словно черпали вдохновение из геометрического смысла эвристик для оценки расстояния в A*. Приятный результат.
+1
Я так понял, в вашем алгоритме необходимо знать координаты цели? Т.е. применить его в случае, когда неизвестно, где ближайший сосед находится, не получится?
0
Ну для таких случаев обычно волновой поиск или алгоритм Дийкстры применяют. По ссылке есть примеры, как они работают.
Приведенный же в статье алгоритм можно применять в контексте игр, когда юниту задают конечную точку пути или когда надо вычислить поле, доступное для хода. На JS с астаром у меня это жрало местами оочень много процессора, что аж подвисало на секунду\другую. Надо попробовать этот алгоритм.
Приведенный же в статье алгоритм можно применять в контексте игр, когда юниту задают конечную точку пути или когда надо вычислить поле, доступное для хода. На JS с астаром у меня это жрало местами оочень много процессора, что аж подвисало на секунду\другую. Надо попробовать этот алгоритм.
0
Алгоритм работает на неориентированном графе единой стоимости. Каждое поле карты имеет <= 8 соседей, которые могут быть проходимы или же нет.
Извините, если что-то не понял, до 8 связей это ограничение алгоритма или примера?
0
Откройте тетрадь в клеточку и посчитайте количество клеток вокруг любой клетки.
+2
человек же не про тетрадь спрашивает а про графы. Можно ли адаптировать алгоритм под граф с 6ю связями?
+1
Спасибо за содержательный ответ!
У автора в аннонсе есть важный момент:
Т.е. алгоритм разменивает возможность А* не делать предположения о структуре графа на уменьшение потребления памяти. Значит, сфера применения этого алгоритма значительно уже, чем у А*.
Это и был ответ на мой вопрос выше, и, как мне кажется, это следует более явно подчеркнуть в статье, потому что предложение про неориентированный граф единой стоимости сбивает с толку.
У автора в аннонсе есть важный момент:
Pathfinding is the problem of navigating from one place to another. My research in this area is primarily focused on single-agent pathfinding problems where the world is represented as a static 2-dimensional grid.
Т.е. алгоритм разменивает возможность А* не делать предположения о структуре графа на уменьшение потребления памяти. Значит, сфера применения этого алгоритма значительно уже, чем у А*.
Это и был ответ на мой вопрос выше, и, как мне кажется, это следует более явно подчеркнуть в статье, потому что предложение про неориентированный граф единой стоимости сбивает с толку.
+2
Спасибо за описание алгоритма!
У меня некое непонимание терминологии возникло: «граф единой стоимости» означает, что все веса равны? Но чуть ниже: «Каждый шаг по направлению (по вертикали или по горизонтали) имеет стоимость 1; шаг по диагонали имеет стоимость √2».
У меня некое непонимание терминологии возникло: «граф единой стоимости» означает, что все веса равны? Но чуть ниже: «Каждый шаг по направлению (по вертикали или по горизонтали) имеет стоимость 1; шаг по диагонали имеет стоимость √2».
+1
Все верно. Длина (вес) шага по диагонали равна длине гипотенузы прямоугольного треугольника с катетами единичной длины.
+1
Является ли переход по диагонали ребром графа?
Является ли граф с разным весом ребер «графом единой стоимости»?
Дайте, пожалуйста, определение графа единой стоимости (гугл, к сожалению, молчит)
Является ли граф с разным весом ребер «графом единой стоимости»?
Дайте, пожалуйста, определение графа единой стоимости (гугл, к сожалению, молчит)
+1
Да, пожалуй с «все верно» я поторопился, вопросы действительно есть.
Пожалуй, не буду пытаться объяснить мое понимание данной ситуации, лучше дождаться пояснения автора статьи.
Пожалуй, не буду пытаться объяснить мое понимание данной ситуации, лучше дождаться пояснения автора статьи.
0
Думаю речь о стоимости/проходимости клеток. А диагональные переходы имеют не стоимость, а коэффициент, чтобы приблизить карту к реальности. Т.е. данный алгоритм не позволяет искать путь в местности, которая содержит поля вперемешку с болотами. Потому как путь напрямую будет дольше, чем обходя болота.
0
«Данный алгоритм представлен в 2011 году, а в 2012 получил высокие отклики.»
Вопрос к хабранароду. Бота для стрелялки можно на таком реализовать? и на сколько это будет эффективно по сравнению с теми же нейросетями?
Вопрос к хабранароду. Бота для стрелялки можно на таком реализовать? и на сколько это будет эффективно по сравнению с теми же нейросетями?
0
Нейросети к ботам для стрелялки никакого отношения не имеют вообще. Алгоритм поиска, о котором тут идет речь, — одна маленькая и не факт, что всегда нужная деталь для бота — зависит от стрелялки.
Вам нужны алгоритмы управления.
Вам нужны алгоритмы управления.
0
Со стрелялкой поторопился, уж больно много она в себя включает. Возьмем к примеру простое передвижение персонажа. Нейросеть по принципу обучения «Туда не ходи, сюда ходи» должна довольно не плохо работать, я не прав? Другое дело что при такой реализации все сводится к кропотливому обучению, либо же к хитро придуманному алгоритму автоматического обучения. В данной же статье описан метод, по которому имея только «маску» карты, мы сможем найти оптимальные пути передвижения.
0
Не правы, нет, в вопросах «куда ходить» — это либо алгоритм поиска, либо алгоритм управления типа reinforcement learning. Второй особенно хорош тем, что является одновременно и алгоритмом поиска, и алгоритмом управления, и самообучающимся алгоритмом.
0
Использовать нейронные сети на данный момент в игровом ИИ — это попытка охотиться на орла с ножом. В том смысле, что нейронные сети требуют обучения, и при этом при малейшем изменении исходных данных или изменения каких-либо игровых коэффициентов — полного переобучения. Учитывая при этом очень низкую скорость обучения НС до приемлемых результатов — фактически это становится невозможным.
Если уж так хочется поиграть с «научным» ИИ в играх — попробуйте посмотреть в сторону генетических алгоритмов. По крайней мере, они могут помочь выработать оптимальную стратегию поведения и заложить ее в программу бота в зависимости от разных наборов входных данных. Но, опять же, для обучения этих ботов для «стрелялки» придется слишком много раз проводить игровые сессии, так что этот путь оптимален скорее для детерминированных игр вроде нард :)
На практике же в игровом ИИ используются обычные портянки с кучей if-ов, case-ов и т.д., поскольку на данный момент только они способны адекватно отвечать требованиям к скорости работы.
Если уж так хочется поиграть с «научным» ИИ в играх — попробуйте посмотреть в сторону генетических алгоритмов. По крайней мере, они могут помочь выработать оптимальную стратегию поведения и заложить ее в программу бота в зависимости от разных наборов входных данных. Но, опять же, для обучения этих ботов для «стрелялки» придется слишком много раз проводить игровые сессии, так что этот путь оптимален скорее для детерминированных игр вроде нард :)
На практике же в игровом ИИ используются обычные портянки с кучей if-ов, case-ов и т.д., поскольку на данный момент только они способны адекватно отвечать требованиям к скорости работы.
0
Правильно я понимаю, что ключевое условие для алгоритма: единая стоимость графа? В случае, если оно не соблюдается — в общем случае — все равно применимым остается А*?
+2
Зарегистрируйтесь на Хабре, чтобы оставить комментарий


Алгоритм поиска пути Jump Point Search