Комментарии 43
Это всё прекрасно. Только я мораль чутка не понял. Чем они так хороши-то, R-функции? С помощью них предлагается строить модели, являющиеся множеством точек, для которых некоторая R-функция, например, положительна?
А эту фразу я вообще не понял:
Можете пояснить?
А эту фразу я вообще не понял:
можем не терять точность на приближенном описании геометрии объекта.
Можете пояснить?
R-функции хороши тем, что мы можем построить аналитическое выражение для любого объекта (в трех или двумерном пространстве). Т.е. проще говоря — можно описывать что угодно. Например, можно знать f(x,y,z) например самолета. А зная функцию можно решать вариационные задачи, при чем точность на приближении описания объекта (например аппроксимировании поверхности как в МКЭ) не теряется
Добавьте, пожалуйста, ссылок на источники.
У вас S_2(t) не определена в нуле. И вообще, как-то все описание нематематично.
да, недочет, исправлю. Описание приведено чтобы ознакомить с методом R-функций. Вообще, моя первая статья) спасибо большое за комментарии!
Самый большой недочет — непонятно о чем речь. Да, ясны определения, да вы вроде написали, как это используют, но все как-то очень расплывчато.
И вообще, говоря «мы можем построить аналитическое выражение для любого объекта (в трех или двумерном пространстве)», вы определенно обманываете. Я могу придумать неизмеримый обьект, вы точно не сможете аналитически его представить.
Да и потом, если вы представляете обьект в виде комбинации R-функций, то его можно представить и без них. В чем же тогда преимущество? Не ясен смысл всего этого.
Приведите пример такого обьекта, который только с помощью R-функций можно описать — тогда все встанет на свои места.
И вообще, говоря «мы можем построить аналитическое выражение для любого объекта (в трех или двумерном пространстве)», вы определенно обманываете. Я могу придумать неизмеримый обьект, вы точно не сможете аналитически его представить.
Да и потом, если вы представляете обьект в виде комбинации R-функций, то его можно представить и без них. В чем же тогда преимущество? Не ясен смысл всего этого.
Приведите пример такого обьекта, который только с помощью R-функций можно описать — тогда все встанет на свои места.
Приведите пример неизмеримого объекта. Точно знаю, что сейчас R-функции используют для раскроя материалов. Понимаете, дело не в том что ТОЛЬКО с помощью метода R-функций. Суть в удобстве и выразительности.
Например вы хотите построить уравнение скажем пешки)
Для этого выберем такие опорные функции:
где 1 — объект, полученный при вращении параболы вокруг Oz,
2 — цилиндр осью которого является ось Oz,
3 — слой, параллельный плоскости xOy,
4 — сфера,
5 — эллипсоид
Легко понять, чтобы получить пешку нужно слепить такой предикат:
В результате получаем:
Например вы хотите построить уравнение скажем пешки)
Для этого выберем такие опорные функции:
где 1 — объект, полученный при вращении параболы вокруг Oz,
2 — цилиндр осью которого является ось Oz,
3 — слой, параллельный плоскости xOy,
4 — сфера,
5 — эллипсоид
Легко понять, чтобы получить пешку нужно слепить такой предикат:
В результате получаем:
т. е. можно интерпретировать процесс рассуждения/построения так: говорите «хочу построить основание пешки. Для этого возьму цилиндр, обрежу его снизу плоскостью и оставлю только ту часть, которая является общей для объекта, полученного при вращении параболы вокруг Oz. Далее объединяю это основание с неким объектом, который в свою очередь представляет объединение сферы и эллипсоида». На выходе получаю f(x,y,z), с которым могу решать задачи теплопроводности (нагревание, остывание пешки), механики (скручивание, разрыв) и т. д.
То есть фактически метод есть разбиение большой и сложной функции на чуть менее большие и сложные?
не совсем. Тут более глубокая суть. Это как конструктор. Но только вы оперируете природной булевой алгеброй и привычными всем функциями, описывающими уравнения. Главная особенность — все прозрачно, легко и понятно.
И еще, в плане стиля статья, честно скажу, отвратительна.
Вы сначала долго говорите про R-функции, приводите 2 столбца, говорите, что левый — такие, правый не такие, и только ближе к середине статьи даете определение. Считай, приходится перечитывать первую половину статьи еще раз — уже знач, о чем речь. Нельзя говорить об обьекте, не дав его определение заранее.
Вы сначала долго говорите про R-функции, приводите 2 столбца, говорите, что левый — такие, правый не такие, и только ближе к середине статьи даете определение. Считай, приходится перечитывать первую половину статьи еще раз — уже знач, о чем речь. Нельзя говорить об обьекте, не дав его определение заранее.
Все жалуются на какие-то непонятки, а я вот что хочу узнать: поскольку R-функции не являются чем-то сверхестесственным, а всего лишь сужением дифференциируемых, должна быть какая-то теорема, оправдывающая определение.
В целом, напоминает гиперразвитую выпуклую геометрию – а конкретно, построение выпуклых многогранников пересечением опорных полупространств афинных функционалов. Спасибо за статью
В целом, напоминает гиперразвитую выпуклую геометрию – а конкретно, построение выпуклых многогранников пересечением опорных полупространств афинных функционалов. Спасибо за статью
Нееет, это не сужение дифференциируемых. В том смысле что существуют недифференциируемые R-функции.
Да хоть \x -> if x <= 0 then -1 else 1. Вполне себе R-функция, но не то что дифференциируемостью, тут и непрерывностью не пахнет.
Да хоть \x -> if x <= 0 then -1 else 1. Вполне себе R-функция, но не то что дифференциируемостью, тут и непрерывностью не пахнет.
ну то что вы написали не является R-функцией. А так под определение можно подогнать конечно любую. Но в статье написано про одну из стандартных систем R-функций, которые являются и дифференцируемыми и непрерывными. Я могу привести пример других систем R-функций, которые обладают всеми хорошими свойствами
Ага, виноват. И все-таки, ткнете в обоснование определения? Я не нашел вашей книжки, но нашел «Рвачев — Геометрические приложение алгебры логики» (отличная, судя по всему, книжка). Я ее пролистал, но глобальной теоремы не увидел. Неясно, почему мы требуем суръекцию множества R-функций на булевы.
То есть границы всё равно должны быть аналитически описаны?
Что вы имеете ввиду? В смысле того что я должен помимо области для построения фигуры знать уравнение границы для каждого примитива?
Ну вот ваш пример с пешкой — почему вы выбрали именно такие опорные области?
на самом деле вариант построения с пешкой не единственен в плане выбора опорных. Для построения я руководствовался тем что видел — вот есть какое то основание, которое могу получить вращение параболы вокруг Oz. И вот возьму сверху к нему прилеплю эллипсоид и сферу. Вот в принципе и вся логика выбора именно таких опорных.
Например вам нужно построить ГО, состоящий из объектов различной размерности (например вам нужно знать уравнение границы полукруга)
Хотим построить уравнение жука:
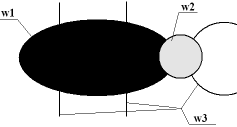
Для этого выберем такие опорные функции:
и изобразим нашу омегу:
Хотим построить уравнение жука:
Для этого выберем такие опорные функции:
и изобразим нашу омегу:
Спасибо автору. Хорошо иногда размять мозги вникая в определения =)
Никогда прежде не сталкивался с R-функциями.
Меня, как математика по образованию смутило ваше определение:
Функция f(x1..xm) называется R-функцией, если булевый знак этой функции равен булевой функции булевых знаков аргументов x1..xm.
Булевых функций, как я понимаю много. Это — целый класс.
Поэтому, я бы сформулировал так:
Функция f называется R-функцией, если существует такая булева функция, что…
Т.е. главные признак — существование такой булевой функции.
Википедия со мной согласна ;)
хотя там, почему-то, вместо булевых знаков используется sign.
Никогда прежде не сталкивался с R-функциями.
Меня, как математика по образованию смутило ваше определение:
Функция f(x1..xm) называется R-функцией, если булевый знак этой функции равен булевой функции булевых знаков аргументов x1..xm.
Булевых функций, как я понимаю много. Это — целый класс.
Поэтому, я бы сформулировал так:
Функция f называется R-функцией, если существует такая булева функция, что…
Т.е. главные признак — существование такой булевой функции.
Википедия со мной согласна ;)
хотя там, почему-то, вместо булевых знаков используется sign.
определение приведено из источника, непосредственно создателя R-функций. Хотя я с вами согласен )
Не сочтите меня говнюком, но я нашел, где можно почитать
Рвачев В.Л. Теория R-функций и некоторые ее приложения
там, на 101 странице дано определение R-отображения, как раз через существование.
вот скрин:
A определение R-функции дано на 111 странице, но уже через R-Отображения.
Рвачев В.Л. Теория R-функций и некоторые ее приложения
там, на 101 странице дано определение R-отображения, как раз через существование.
вот скрин:
A определение R-функции дано на 111 странице, но уже через R-Отображения.
да, спасибо. Вот только хотел ответить ckald примерно этой же ссылкой). Просто такое определение для более узкого круга людей)
Спасибо за статью, очень интересно, однако вам определенно стоит поработать над стилем.
1. Так в чем же заключается обратная задача аналитической геометрии? Насколько я понял из Википедии — в построении по картинке уравнения, точки решений которого составят исходный рисунок. Конечно, очевидно, что аппарат R-функций очень удобен для большинства встречающихся в технике конктрукций, но существует ли соответствующий формальный алгоритм?
Посмотреть указанную в конце статьи программку не могу — к сожалению, у меня нет Windows.
2. Для генерации картинок-формул удобно использовать сервисы из обзора habrahabr.ru/blogs/latex/100938/ — намного более качественные изображения получаются.
1. Так в чем же заключается обратная задача аналитической геометрии? Насколько я понял из Википедии — в построении по картинке уравнения, точки решений которого составят исходный рисунок. Конечно, очевидно, что аппарат R-функций очень удобен для большинства встречающихся в технике конктрукций, но существует ли соответствующий формальный алгоритм?
Посмотреть указанную в конце статьи программку не могу — к сожалению, у меня нет Windows.
2. Для генерации картинок-формул удобно использовать сервисы из обзора habrahabr.ru/blogs/latex/100938/ — намного более качественные изображения получаются.
Круто осозновать, что есть ученый с твоей фамилией ;)
А каково практическое применение этому?
Хорошо, мы можем получить описание сложной геометрической формы в виде функции положительной внутри, отрицательной снаружи и нулевой на границе. Потому о любой точке мы можем сказать где она расположена, и даже дать оценку как далеко она от границе по модулю значения этой функции. Ну и какие задачи это позволяет решать?
Какие сведения об объекте можно извлечь из этой функции?
Нет, конечно можно и картинку нарисовать, и еще много чего сделать, но ведь это «подметать плац лопатами», потому что все эти задачи решаются гораздо более эффективно другими методами.
Хотелось бы услышать задачу, где представление с помощью R-функций если не даст фору, то хотя бы не будет уступать другим подходам.
Хорошо, мы можем получить описание сложной геометрической формы в виде функции положительной внутри, отрицательной снаружи и нулевой на границе. Потому о любой точке мы можем сказать где она расположена, и даже дать оценку как далеко она от границе по модулю значения этой функции. Ну и какие задачи это позволяет решать?
Какие сведения об объекте можно извлечь из этой функции?
Нет, конечно можно и картинку нарисовать, и еще много чего сделать, но ведь это «подметать плац лопатами», потому что все эти задачи решаются гораздо более эффективно другими методами.
Хотелось бы услышать задачу, где представление с помощью R-функций если не даст фору, то хотя бы не будет уступать другим подходам.
все дело в том что используя метод R-функций вы получаете точное уравнение области, без каких либо приближений. Далее вариационным методом можно решить любую задачу… RFM, в разработке которой я принимаю участие, например потеря точности решения происходит лишь при интегрировании. На самом деле используя атомарные функции можно добиться максимально низкой потери точности решения
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Решение обратной задачи аналитической геометрии. Теория R-функций