Комментарии 38
> Эти линии будут делить исходный угол на три равные части
нет не будут
нет не будут
«Эти линии будут делить исходный угол на три равные части». Эти линии будут делить основание треугольника на три равные части, но кто сказал, что они будут делить угол на три равных угла?
Точно сейчас не скажу, но по-моему это логично, что напротив равных сторон будут находиться равные углы. Я не прав?
Нет. Это неправда, но для того, чтоб отмести доказательство достаточно, что это ниоткуда не следует. Автору доказательства следует самостоятельно доказывать все логические переходы, а не писать «очевидно», «логично».
Как контрпример — попробуйте повторить с тупым углом, там будет нагляднее.
Как контрпример — попробуйте повторить с тупым углом, там будет нагляднее.
Это и есть ваша ошибка.
Сравните «большой красный треугольник» и треугольник слева от него. Одна сторона у них равна (она общая). Основания равны по построению. Допустим, что и углы при вершине равны, тогда ОБЯЗЯТЕЛЬНО будет равны и третьи стороны треугольников. Даже на рисунке видно, что это не так.
Сравните «большой красный треугольник» и треугольник слева от него. Одна сторона у них равна (она общая). Основания равны по построению. Допустим, что и углы при вершине равны, тогда ОБЯЗЯТЕЛЬНО будет равны и третьи стороны треугольников. Даже на рисунке видно, что это не так.
Если я правильно понял про треугольники которые Вы берете, то Вы не правы. Для равенства треугольников нужен угол между равными сторонами, а Вы берете 2 стороны и какой-то угол.
К Автору: для удобство обсуждения хорошо бы именовать вершины, а то описания типа «ну тот большой красный» не очень однозначно.
К Автору: для удобство обсуждения хорошо бы именовать вершины, а то описания типа «ну тот большой красный» не очень однозначно.
У меня на рисунке есть обозначения
Подобие / равенство треугольников идет по 2м сторонам и углу МЕЖДУ ними, поэтому Ваше «обязательно» не сильно отличается от допущений, которые привел автор.
Другое дело, что по теореме синусов мы сможем доказать что эти стороны обязательно должны были быть равными (использовав дополнительно еще тот факт, что 2 равных стороны образуют одну прямую по построению).
Другое дело, что по теореме синусов мы сможем доказать что эти стороны обязательно должны были быть равными (использовав дополнительно еще тот факт, что 2 равных стороны образуют одну прямую по построению).
Допущение имеет смысл, если требуемый угол является вершиной равнобедренного треугольника.
Тогда разделив основание на три равнй отрезка и проведя через вершину и отмеченные точки векторы получаем угол, деленный на три сектора.
Нюанс в том, что указанное выше решение работает только для равностороннего треугольника, у которого и углы также равны. Тогда отложив по три части на двух гранях можем получить простым построением третью, которая равна двум другим. Если же исходный угол больше или меньше 60 градусов, равносторонний треугольник превращается в равнобедренный, а значит третью грань равную первым двум построить нельзя.
Тогда разделив основание на три равнй отрезка и проведя через вершину и отмеченные точки векторы получаем угол, деленный на три сектора.
Нюанс в том, что указанное выше решение работает только для равностороннего треугольника, у которого и углы также равны. Тогда отложив по три части на двух гранях можем получить простым построением третью, которая равна двум другим. Если же исходный угол больше или меньше 60 градусов, равносторонний треугольник превращается в равнобедренный, а значит третью грань равную первым двум построить нельзя.
Простите за мой французский, но что за ху*ню вы все несёте? Это не будет работать ни для равнобедреного, ни для равностороннего треугольника. Векторы, сектора… Что ещё приплести из геометрии, о которой уже никто ничего не помнит.
Просто перечитайте эти комментарии. 1 2. Поколение СЕОшников блин. Извините накипело.
Просто перечитайте эти комментарии. 1 2. Поколение СЕОшников блин. Извините накипело.
Нуну, продолжайте сливать, да здравствует мракобесие и толерантность.
При чем тут СЕОшники?
Можно еще школоту упомянуть, странно почему не приплели…
Не то, чтобы я совсем ничего не помнил, но человеку свойственно заблуждаться.
Таки был неправ. Угол подобным построением можно поделить максимум пополам, при условии равнобедренности.
На три и больше таки не получится
Можно еще школоту упомянуть, странно почему не приплели…
Не то, чтобы я совсем ничего не помнил, но человеку свойственно заблуждаться.
Таки был неправ. Угол подобным построением можно поделить максимум пополам, при условии равнобедренности.
На три и больше таки не получится
Школьник наверняка ещё что-то помнит из геометрии (ну я надеюсь на это), так что это как раз не в тему. Да тут даже помнить ничего не надо, просто мозг включить и читать внимательно.
Современные школьники — к сожалению печаль и грусть в концентрированном виде в большинстве случаев (точнее их знания).
С памятью у меня вполне неплохо, и геометрию учил (хоть и уже достаточно давненько). Но вот, честно говоря, не помню, чтобы мы решали подобные задачки на уроках.
Я ошибки признавать могу — да, был неправ, недоглядел.
Но это не значит, что надо вот так сразу оскорблениями кидаться.
С памятью у меня вполне неплохо, и геометрию учил (хоть и уже достаточно давненько). Но вот, честно говоря, не помню, чтобы мы решали подобные задачки на уроках.
Я ошибки признавать могу — да, был неправ, недоглядел.
Но это не значит, что надо вот так сразу оскорблениями кидаться.
ВНИМАНИЕ!
Я прошу прощения у compdemon за то, что косвенно отнёс его к поколению СЕОшников, т.е. к множеству современников, типичные задачи которых лежат в области поисковой оптимизации. У меня не было оснований так обобщать и вешать на compdemon ярлыки.
В оправдание могу сказать, что изначально мне казалось что ошибочные комментарии в этом посте принадлежат совсем разным людям и я обеспокоился о судьбе человечества. Как оказалось большинство из них принадлежат одному человеку, compdemon, и он свои ошибки признал.
Спасибо за внимание.
Я прошу прощения у compdemon за то, что косвенно отнёс его к поколению СЕОшников, т.е. к множеству современников, типичные задачи которых лежат в области поисковой оптимизации. У меня не было оснований так обобщать и вешать на compdemon ярлыки.
В оправдание могу сказать, что изначально мне казалось что ошибочные комментарии в этом посте принадлежат совсем разным людям и я обеспокоился о судьбе человечества. Как оказалось большинство из них принадлежат одному человеку, compdemon, и он свои ошибки признал.
Спасибо за внимание.
Вы правы, углы равными не будут
Архимедова спираль позволяет сделать трисекцию угла. Вот бы ещё спираль с помощью циркуля и линейки построить…
А как на нижнем отрезке деление происходит?
Описанное условие подходит только для равностороннего треугольника.
Как быть с острым или тупым углом?
(Картинку вставить не дает карма, так что ссылка): piccy.info/view3/1662490/3d5c8a2abda1c6b110d6283f43627f8f/
Проблема в задаче — именно разделить нижний отрезок на три равные части. Особенно если учесть, что дробь 1/3 является бесконечной периодической. :)
Описанное условие подходит только для равностороннего треугольника.
Как быть с острым или тупым углом?
(Картинку вставить не дает карма, так что ссылка): piccy.info/view3/1662490/3d5c8a2abda1c6b110d6283f43627f8f/
Проблема в задаче — именно разделить нижний отрезок на три равные части. Особенно если учесть, что дробь 1/3 является бесконечной периодической. :)
А как на нижнем отрезке деление происходит?
Поместится как раз три отрезка, т.к. эти треугольники подобны в отношении 1 к 3
Как раз нижний отрезок, автор разделил на три равные части. Причем решение было и простое и красивое.
И причем тут тот факт, что дробь 1/3 является бесконечной периодической в ДЕСЯТИЧНОЙ системе исчисления? В троичной, например, она не будет периодической. Да и вообще алгебраическая форма записи чисел, имеет мало смысла в чисто геометрической задаче.
И причем тут тот факт, что дробь 1/3 является бесконечной периодической в ДЕСЯТИЧНОЙ системе исчисления? В троичной, например, она не будет периодической. Да и вообще алгебраическая форма записи чисел, имеет мало смысла в чисто геометрической задаче.
Ладно, откидываем алгебру — таки не к месту.
Вопрос в том — КАК автор разделил нижнюю грань на ТРИ ОДИНАКОВЫХ отрезка? :)
В случае с углом 60 градусов, когда получаем РАВНОСТОРОННИЙ треугольник, по двум граням можно построить третью, так как они равны. В случае с РАВНОБЕДРЕННЫМ, когда равны только две грани (а с учетом изложенного построение и приняв исходный угол за вершину такого треугольника, нижняя грань, построенная при угле отличном от 60 градусов будет отличаться), вопрос — КАК разделить третью, полученную, грань на ТРИ РАВНЫХ отрезка?
Вопрос в том — КАК автор разделил нижнюю грань на ТРИ ОДИНАКОВЫХ отрезка? :)
В случае с углом 60 градусов, когда получаем РАВНОСТОРОННИЙ треугольник, по двум граням можно построить третью, так как они равны. В случае с РАВНОБЕДРЕННЫМ, когда равны только две грани (а с учетом изложенного построение и приняв исходный угол за вершину такого треугольника, нижняя грань, построенная при угле отличном от 60 градусов будет отличаться), вопрос — КАК разделить третью, полученную, грань на ТРИ РАВНЫХ отрезка?
Думаю так понятнее, какой изначально треугольник, равносторонний или нет, не имеет значения
Попытаюсь опровергнуть.
Дано:
AF1=F1F2=F2C;
AB=BC;
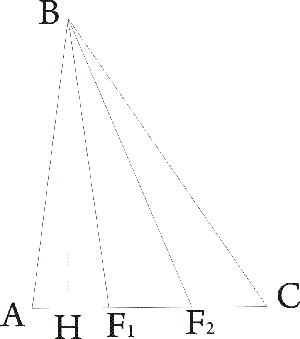
P.S. мог и ошибиться
Дано:
AF1=F1F2=F2C;
AB=BC;
Опустим высоту BH;
S(ABF1)=S(F1BF2)=S(F2BFC)=BH*AF1 (Т.к. AF1=F1F2=F2C) (1)
C другой стороны:
S(ABF1)=AB*BF1*sin(ABF1)
S(F1BF2)=BF2*BF1*sin(F1BF2)
Т.к. S(ABF1)= S(F1BF2) (по 1), то AB*BF1*sin(ABF1)=BF2*BF1*sin(F1BF2) (2)
Пред. уг. ABF1 = уг. F1BF2, тогда sin(ABF1)=sin(F1BF2), тогда из этого и (2) следует, что AB=BF2.
Аналогично BC=BF1=>AB=BF1=BF2=BC =>AC - дуга окр. с ц. BP.S. мог и ошибиться
У автора по построению еще и AB = BC.
Но рассуждения правильные.
Но рассуждения правильные.
ВСЯ ФИШКА В ТОМ, ЧТО АВТОР ПОСТРОИЛ РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК СНАЧАЛА!!! А ТУТ РИСУЮТ КАКУЮ-ТО ХУ*НЮ НЕРАВНОБЕДРЕННУЮ!!!
Пардоньте за капс, накипело, 95% комментов к посту — хрень полная и никчемные попытки опровержения. Меня вот интересует наглядный результат проверки работы этого способа с тупым углом, и я больше не могу, пошел проверять сам…
Но в случае с острым — решение работает!
Пардоньте за капс, накипело, 95% комментов к посту — хрень полная и никчемные попытки опровержения. Меня вот интересует наглядный результат проверки работы этого способа с тупым углом, и я больше не могу, пошел проверять сам…
Но в случае с острым — решение работает!
Ну что же…
kroks вполне годное доказательство привел, оно работает на 100% как в случае острого, равнобедренного, так и тупого угла.
Да, он криво построил. Но это ни чуть не мешает это доказать, для математика построение имеет второстепенное значение, основа — рассуждения, доказательство.
P.S. я совершил ту же ошибку — глядя на построение сказал указал на ошибку построения, что AB = BC. Но это же kroks привел в «Дано».
kroks вполне годное доказательство привел, оно работает на 100% как в случае острого, равнобедренного, так и тупого угла.
Да, он криво построил. Но это ни чуть не мешает это доказать, для математика построение имеет второстепенное значение, основа — рассуждения, доказательство.
P.S. я совершил ту же ошибку — глядя на построение сказал указал на ошибку построения, что AB = BC. Но это же kroks привел в «Дано».
Нет такого угла, для которого рабоатет. Просто в случае острого угла у человека, забывшего геометрию, создаётся иллюзия, что все три угла равны.
Не совсем согласен)))
Но считать ли за угол угол в 0 градусов?
Но считать ли за угол угол в 0 градусов?
Шутку оценил.
Задача о трисекции действительно разрешима для некоторых углов. Однако, нет такого угла, трисекцию которого можно было бы осуществить способом, предложенным автором.
Задача о трисекции действительно разрешима для некоторых углов. Однако, нет такого угла, трисекцию которого можно было бы осуществить способом, предложенным автором.
С нетерпением жду также «решений» задач о квадратуре круга, удвоении куба и создании вечного двигателя
Точно такую же ошибку сделала в 8 классе, когда впервые услышала про эту задачу :-)
Эта задача разрешима только при определенных значениях угла (см. Википедию, например)
При остальных — неразрешима.
Доказано :)
При остальных — неразрешима.
Доказано :)
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Трисекция угла