
Постройте выпуклый восьмиугольник с четырьмя прямыми углами.
Вероятно, то, что я даю такие задания, многое говорит обо мне, как об учителе. Я наблюдаю за тем, как студенты пытаются выстроить прямые углы последовательно. Когда у них это не получается, они пытаются перемежать прямые углы. Снова потерпев неудачу, они вставляют их в многоугольник случайным образом. Скрежет, издаваемый их мозгами во время мыслительных усилий — музыка для ушей учителя.
Потом у них возникают подозрения и они начинают задавать вопросы. «Вы сказали о прямых углах. Может, на самом деле вы имели в виду три угла?», «Вы точно имели в виду выпуклый многоугольник?», «Четыре прямых угла, по сути, образуют прямоугольник. Как мы можем получить ещё четыре стороны в восьмиугольнике?» Я внимательно слушаю, киваю, подтверждая их догадки.
Наконец, кто-то задаёт вопрос, который никто не осмеливался задать, вопрос, которого я ждал: «Слушайте, а это вообще возможно?»
Этот вопрос обладает мощью, способной менять образ мышления в математике. Те, кто думал узко о конкретных условиях, теперь должны думать более широко о том, как соответствуют друг другу эти условия. Те, кто работает внутри системы, должны сделать шаг назад и изучить саму систему. На протяжении всей истории математики этот вопрос задавался множество раз, им озадачивались те, кто решал задачи квадратуры круга для обхождения города Кёнигсберга. И этот вопрос позволяет нам сформулировать, что же такое математика и как мы её понимаем.
Например, поиск восьмиугольника с определёнными свойствами сильно отличается от задачи демонстрации, что такого восьмиугольника существовать не может. Экспериментируя с разными восьмиугольниками, мы ведь можем и наткнуться на такой, где есть четыре прямых угла.
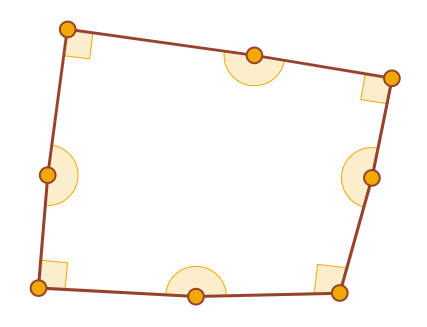
Это не пример. На самом деле у этого восьмиугольника нет четырёх прямых углов.
Но удача не играет никакой роли в доказательстве того, что подобный восьмиугольник не может существовать. Для него требуется глубокое знание, не только многоугольников, но и самой математики. Чтобы учесть невозможность, нам нужно понять, что простое допущение о существовании объекта не доказывает его существование. Математические определения, свойства и теоремы живут в условиях давления, вызванного их взаимосвязанностью. Пытаясь представить восьмиугольник с четырьмя прямыми углами, мы находимся внутри этих взаимосвязанных правил.
Но чтобы осознать, что восьмиугольник невозможен, нам нужно отступить на шаг назад и взглянуть на картину в целом. Какие математические и геометрические принципы могут быть нарушены восьмиугольником с четырьмя прямыми углами? Здесь хорошо будет начать с теоремы о сумме углов многоугольника.
Сумма внутренних углов n-стороннего многоугольника определяется по формуле:
S = (n – 2) × 180º
Так получилось, потому что каждый n-сторонний многоугольник можно разрезать на (n − 2) треугольников, сумма внутренних углов каждого из которых равна 180º.
В случае восьмиугольника это означает, что сумма его внутренних углов равна (8 – 2) × 180º = 6 × 180º = 1080º. Тогда если четыре из его углов прямые, то есть каждый равен 90º, то это составляет 4 × 90º = 360º от общей суммы углов. Значит, на оставшиеся четыре угла восьмиугольника остаётся 1080º – 360º = 720º.
Это означает, что среднее для четырёх оставшихся углов должно быть равно:
Но внутренние углы выпуклого многоугольника должны быть меньше 180º, то есть это невозможно. Выпуклый восьмиугольник с четырьмя прямыми углами не может существовать.
Доказательство невозможности таким способом требует сделать шаг назад и посмотреть, как различные математические правила, например, формула суммы углов многоугольника и определение выпуклого многоугольника, существуют во взаимном давлении. И поскольку доказательства невозможности полагаются на более широкое рассуждение над множеством правил, часто существует несколько способов построения такого доказательства.
Давайте вернёмся к нашему предыдущему замечанию о том, что четыре прямых угла составляют прямоугольник.
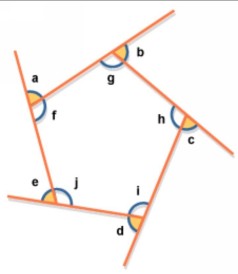
Внешние углы многоугольника.
Если бы восьмиугольник имел четыре прямых угла, то обойдя только эти углы, мы бы совершили полный круг, как будто мы полностью обошли вокруг прямоугольника. Эта мысль приводит нас к правилу, дающему ещё одно доказательство невозможности. Известно, что сумма внешних углов выпуклого многоугольника всегда равна 360º. Поскольку внешний угол прямого угла также является прямым углом, наши четыре прямых угла составят все 360º от суммы внешних углов восьмиугольника. То есть остальным четырём углам не остаётся ничего, и мы снова установили, что такой восьмиугольник невозможен.
Доказательство того, что что-то невозможно — мощное математическое событие. Оно сдвигает нашу точку зрения, мы превращаемся из подчиняющихся правилам в контролирующих правила. А чтобы контролировать правила, нам нужно сначала их понять. Мы должны не только знать, как применять их, но и ситуации, в которых они неприменимы. А также находить ситуации, в которых правила могут конфликтовать друг с другом. В процессе исследования восьмиугольника мы выявили взаимосвязь многоугольников, выпуклости, прямых углов и сумм углов. И это подчёркивает, что S = (n – 2) × 180º — не просто формула: это одно из условий в мире конфликтующих условий.
Доказательства невозможности могут помочь нам лучше понимать все области математики. В школе уроки по теории вероятностей часто начинаются с подбрасывания множества воображаемых монеток. Я предлагаю ученикам создать жульническую монету, имеющую склонность к выпадению орла или решки, обладающую следующим свойством: при подбрасывании монетки дважды результаты двух подбрасываний с большей вероятностью будут разными, чем одинаковыми. Другими словами, вы с большей вероятностью выбросите орла и решку, чем орла и орла или решку и решку.
После экспериментов и мыслительных неудач ученики приходят к интересной гипотезе: разные результаты никогда не имеют бОльшую вероятность, чем одинаковые. Алгебра выявляет это и указывает на лежащую в основе этого явления симметрию.
Допустим, монетка смещена в сторону выпадания орла. Мы назовём вероятность выпадания орла
Если мы подбросим монету дважды, то вероятность получения двух орлов или двух решек будет равна
Здесь мы складываем вероятность получения двух орлов (левая часть) с вероятностью получения двух решек (правая часть). При помощи алгебры мы можем упростить вероятность получения одинакового результата при обоих бросках:
Поскольку
Как и в случае задачи с многоугольником, мы видим работу конкурирующих математических давлений: изменение вероятности получения одной стороны монеты изменяет вероятность получения другой, и эта взаимосвязанность управляет пространством возможностей результатов двух бросков. Мы выявили это давление, пытаясь выполнить невозможное.
Таким давлениям можно подвергнуть любую область математики. Попробуйте найти шесть последовательных целых чисел, сумма которых равна 342, и благодаря своей настойчивости вы придёте к более глубокому пониманию чётности. (Тот факт, что последовательные целые числа попеременно становятся чётными и нечётными, влияет на то, какими могут быть их суммы.) Нахождение кубического многочлена с целочисленными коэффициентами, имеющего три невещественных корня, научит вас важности сопряжённых комплексных чисел — пар комплексных чисел, произведение и сумма которых всегда вещественны. А если вы попытаетесь вписать в окружность непрямоугольный ромб, то обнаружите важное свойство циклических четырёхугольников — противоположные углы четырёхугольника, вершины которого лежат на окружности, должны иметь сумму 180 градусов.
Столкновение с невозможным позволяет нам исследовать границы наших математических миров. Невозможное само по себе является своего рода обобщением, поэтому естественно будет продолжить обобщение: восьмиугольник не может иметь четырёх прямых углов, но как насчёт десятиугольника? Как насчёт выпуклого многоугольника с n > 4 сторонами? Подобные вопросы упираются в границы наших математических миров и углубляют их понимание.
Если мы будем продавливать границы дальше, то невозможное может даже вдохновить к созданию новых математических миров. Чтобы доказать невозможность получения квадратуры круга (этой задаче уже не менее двух тысяч лет), необходима современная теория трансцендентных чисел, которые не могут являться корнями целочисленных многочленов. Для решения задачи о семи кёнигсбергских мостах Эйлер превратил острова и мосты в вершины и рёбра, дав жизнь обширным областям теории графов и теории сетей, а также множеству их сфер применения. Получение квадратного корня от −1 привело к созданию совершенно новой системы арифметики. А логик Курт Гёдель навсегда изменил математику, доказав, что невозможно доказать, что всё истинное истинно.
Поэтому когда в следующий раз вы столкнётесь с математической задачей, спросите себя: «Возможно ли это?» Столкновение с невозможностью может дать вам более глубокое понимание того, что возможно. При этом вы даже сможете создать новые области математики.
Упражнения
1. Найти площадь треугольника с длинами сторон 46, 85 и 38.
2. Пусть
3. Найти полный квадрат, в котором все составляющие его цифры принадлежат множеству {2, 3, 7, 8}.
Ответы
Ответ 1
Такой треугольник не существует. Длины его сторон не удовлетворяют теореме неравенства треугольника, гласящей, что сумма любых двух сторон должна быть больше третьей. Это можно показать геометрически: возьмём отрезок длиной 85 и на его концах построим окружности радиусами 38 и 46. Эти окружности не пересекутся, из-за чего невозможно найти третью вершину треугольника.
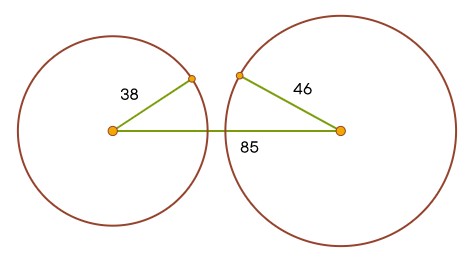
Любопытно будет применить что-нибудь типа формулы Герона для вычисления площади этого не-треугольника. Из этого последуют интересные вопросы!
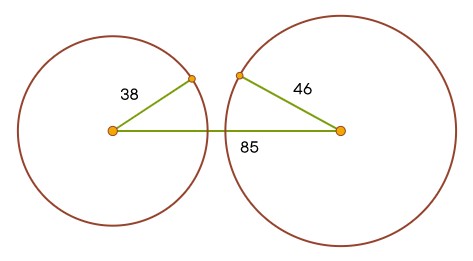
Любопытно будет применить что-нибудь типа формулы Герона для вычисления площади этого не-треугольника. Из этого последуют интересные вопросы!
Ответ 2
Существуют различные способы определения невозможности такого многочлена. Например, эти условия нарушают теорему о рациональных корнях, гласящую, что любые рациональные корни многочлена должны быть соотношением делителя свободного члена (d) и делителя старшего коэффициента (2).
Ответ 3
Любопытный факт о полных квадратах доказывает нам, что эта задача невозможна. В разряде единиц полного квадрата могут быть только цифры 0, 1, 4, 5, 6 или 9. Это можно показать возведением в квадрат каждой возможной цифры и наблюдением за возможными результатами. Поскольку ни один полный квадрат не может заканчиваться на 2, 3, 7 или 8, не существует полного квадрата, состоящего только из этих цифр.
На правах рекламы
Какими бы не были ваши задачи, всегда не помешают доступные и надёжные серверы. Даже для сложных математических расчётов, максимальная конфигурация — 128 ядер CPU, 512 ГБ RAM, 4000 ГБ NVMe.
