В прошлой новости про принципы работы коллекторов логов PostgreSQL я упомянул, что одним из недостатков pull-модели является необходимость динамической балансировки нагрузки. Но если делать ее аккуратно, то недостаток превращается в достоинство, а система в целом становится гораздо более устойчивой к изменениям потока данных.

Давайте посмотрим, какие решения есть у этой задачи.
Чтобы не углубляться в неинтересные абстракции, будем рассматривать на примере конкретной задачи — мониторинга. Соотнести предлагаемые методики на свои конкретные задачи, уверен, вы сможете самостоятельно.
В качестве примера можно привести наши коллекторы метрик для Zabbix, которые исторически имеют с коллекторами логов PostgreSQL общую архитектуру.
И правда, каждый объект мониторинга (хост) генерирует для zabbix практически стабильно один и тот набор метрик с одной и той же частотой все время:

Как видно на графике, разница между min-max значениями количества генерируемых метрик не превышает 15%. Поэтому мы можем считать все объекты равными в одинаковых «попугаях».
В отличие от предыдущей модели, для коллекторов логов наблюдаемые хосты совсем не являются однородными.
Например, один хост может генерировать в лог миллион планов за сутки, другой десятки тысяч, а какой-то — и вовсе единицы. Да и сами эти планы по объему и сложности и по распределению во времени суток сильно отличаются. Так и получается, что нагрузку сильно «качает», в разы:

Ну, а раз нагрузка может меняться настолько сильно, то надо учиться ей управлять…
Сразу понимаем, что нам явно понадобится масштабирование системы коллекторов, поскольку один отдельный узел со всей нагрузкой когда-то точно перестанет справляться. А для этого нам потребуется координатор — тот, кто будет управлять всем зоопарком.
Получается примерно такая схема:
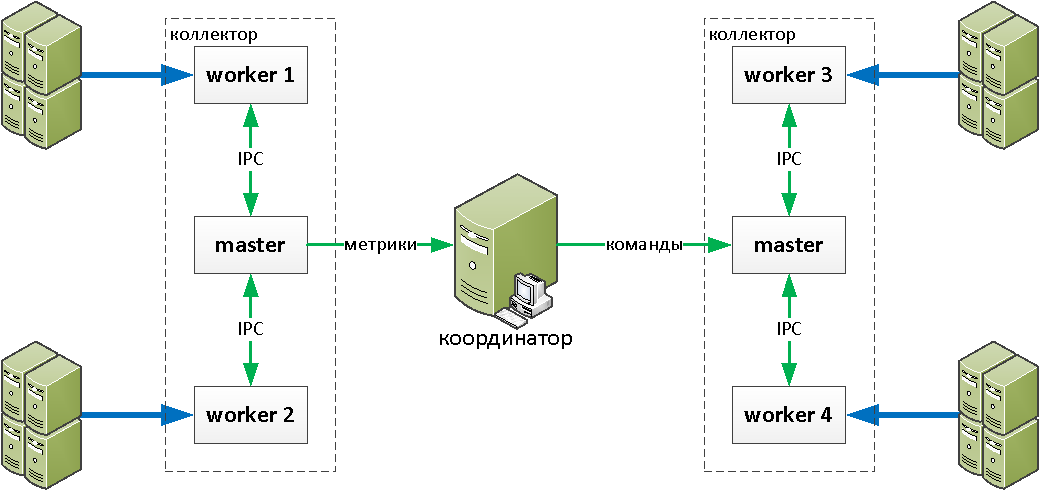
Каждый worker свою нагрузку «в попугаях» и в процентах CPU периодически сбрасывает master'у, те — коллектору. А он, на основании этих данных, может выдать команду типа «новый хост посадить на ненагруженный worker#4» или «hostA надо пересадить на worker#3».
Тут еще надо помнить, что, в отличие от объектов мониторинга, сами коллекторы имеют вовсе не равную «мощность» — например, на одном у вас может оказаться 8 ядер CPU, а на другом — только 4, да еще и меньшей частоты. И если нагрузить их задачами «поровну», то второй начнет «затыкаться», а первый — простаивать. Отсюда и вытекают…
По сути, задача всего одна — обеспечивать максимально равномерное распределение всей нагрузки (в %cpu) по всем доступным worker'ам. Если мы сможем решить ее идеально, то и равномерность распределения %cpu-нагрузки по коллекторам получим «автоматом».
Понятно, что, даже если каждый объект генерирует одинаковую нагрузку, со временем какие-то из них могут «отмирать», а какие-то возникать новые. Поэтому управлять всей ситуацией надо уметь динамически и поддерживать баланс постоянно.
Простую задачу (zabbix) мы можем решить достаточно банально:

Но что делать в случае «сильно неравных» объектов, как для коллектора логов?..
Выше мы все время употребляли термин "максимально равномерное распределение", а как вообще можно формально сравнить два распределения, какое из них «равномернее»?
Для оценки равномерности в математике давно существует такая вещь как среднеквадратичное отклонение. Кому лениво вчитываться:
Поскольку количество worker'ов на каждом из коллекторов у нас тоже может отличаться, то нормировать разброс по нагрузке надо не только между ними, но и между коллекторами в целом.
То есть распределение нагрузки по worker'ам двух коллекторов
Поэтому введем единую метрику-расстояние для общей оценки «равномерности»:
Если бы объектов у нас было немного, то мы могли бы полным перебором «разложить» их между worker'ами так, чтобы метрика оказалась минимальной. Но объектов у нас — тысячи, поэтому такой способ не подойдет. Зато мы знаем, что коллектор умеет «перемещать» объект с одного worker'а на другой — давайте этот вариант и смоделируем, используя метод градиентного спуска.
Понятно, что «идеальный» минимум метрики мы так можем и не найти, но локальный — точно. Да и сама нагрузка может изменяться во времени настолько сильно, что искать за бесконечное время «идеал» абсолютно незачем.
То есть нам осталось всего лишь определить, какой объект и на какой worker эффективнее всего «переместить». И сделаем это банальным переборным моделированием:
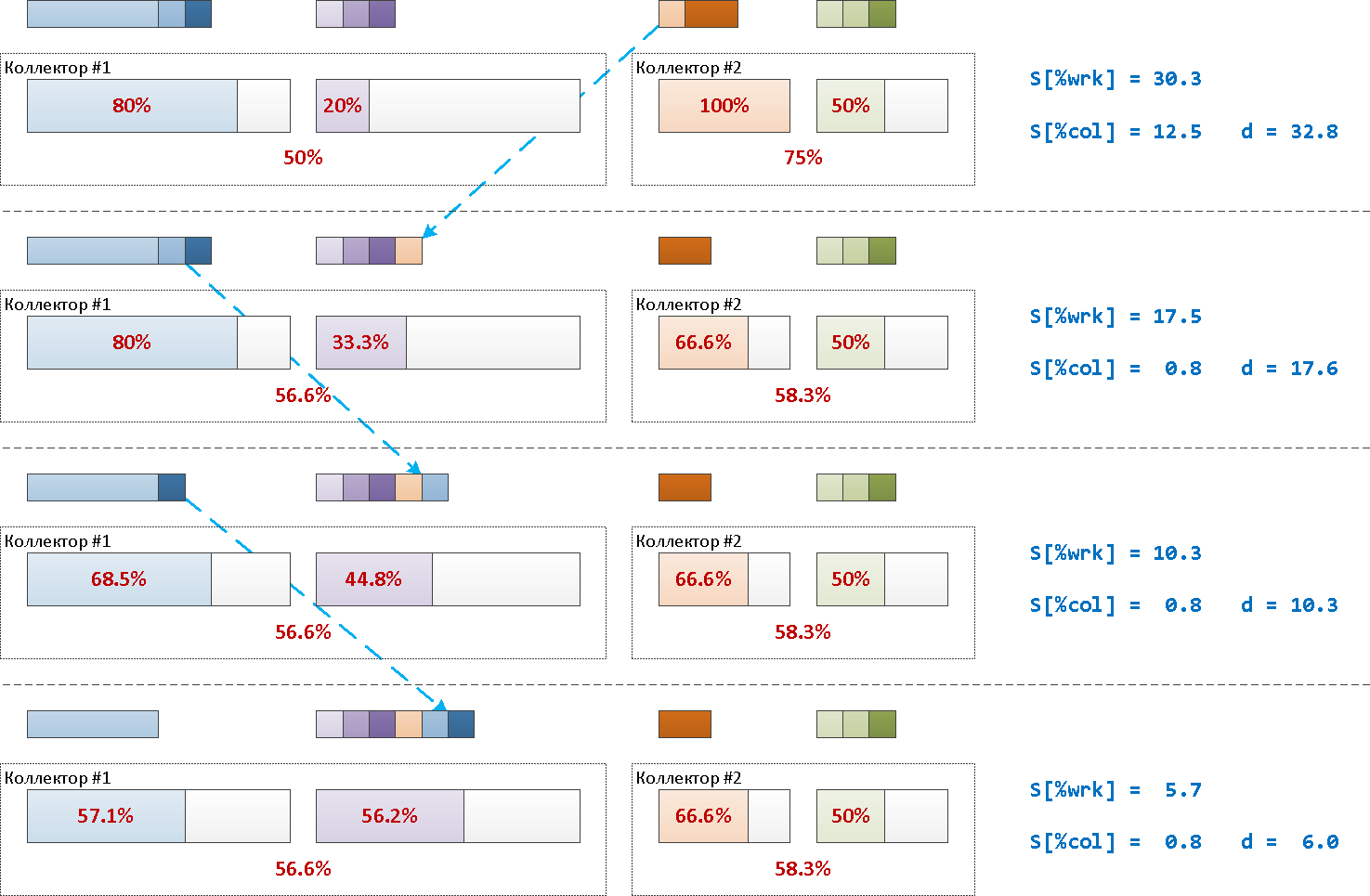
Выстраиваем все пары по возрастанию метрики. В идеале, нам всегда стоит реализовать перенос именно первой пары, как дающий минимальную целевую метрику. К сожалению, в реальности сам процесс переноса «стоит ресурсов», поэтому не стоит запускать его для одного и того же объекта чаще определенного интервала «охлаждения».
В этом случае мы можем взять вторую, третью,… по рангу пару — лишь бы целевая метрика уменьшалась относительно текущего значения.
Если же уменьшать некуда — вот он локальный минимум!
Пример на картинке:
Запускать итерации «до упора» при этом вовсе не обязательно. Например, можно делать усредненный анализ нагрузки на интервале 1 мин, и по его завершению делать единственный перенос.
Понятно, что алгоритм со сложностью
Если на замеренном интервале объект/задача/хост сгенерировал нагрузку «0 штук», то его не то что перемещать куда-то — его даже рассматривать и анализировать не надо.
При генерации пар нет необходимости оценивать эффективность переноса объекта на тот же самый worker, где он и так находится. Все-таки уже будет
Поскольку мы моделируем все-таки перенос именно нагрузки, а объект — всего лишь инструмент, то пробовать переносить «одинаковый» %cpu нет смысла — значения метрик останутся точно те же, хоть и для другого распределения объектов.
То есть достаточно оценить единственную модель для кортежа (wrkSrc, wrkDst, %cpu). Ну, а «одинаковыми» вы можете считать, например, значения %cpu, совпадающие до 1 знака после запятой.
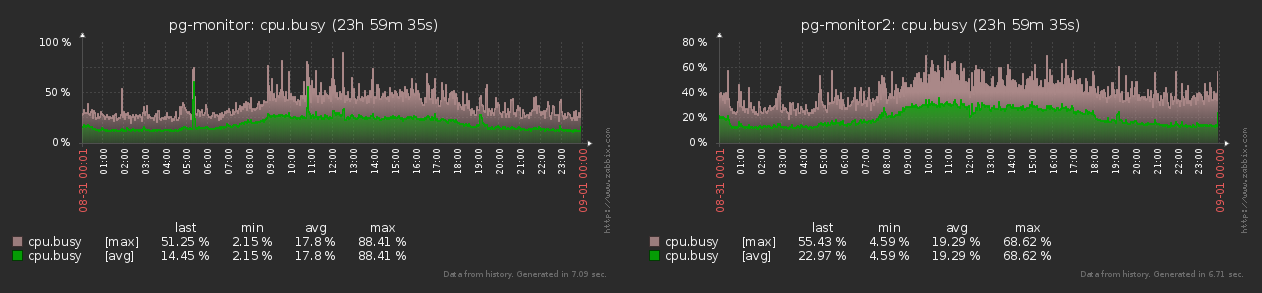
В результате, нагрузка по нашим коллекторам распределяется практически одинаково в каждый момент времени, оперативно нивелируя возникающие пики:
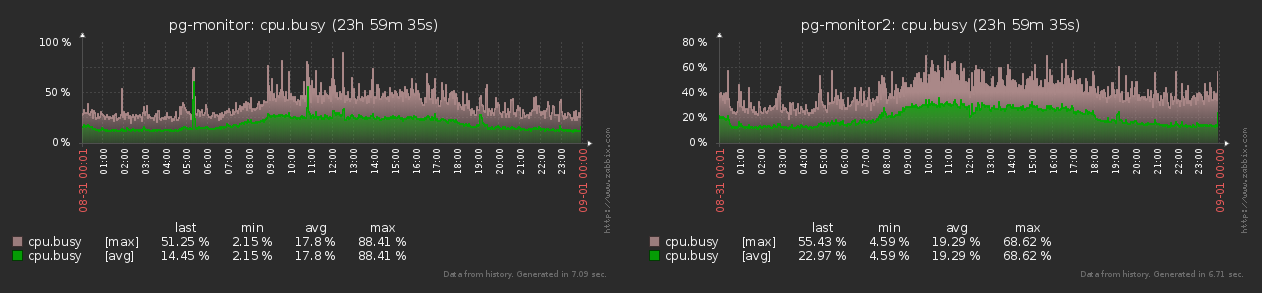

Давайте посмотрим, какие решения есть у этой задачи.
Распределение объектов «по мощности»
Чтобы не углубляться в неинтересные абстракции, будем рассматривать на примере конкретной задачи — мониторинга. Соотнести предлагаемые методики на свои конкретные задачи, уверен, вы сможете самостоятельно.
«Равномощные» объекты мониторинга
В качестве примера можно привести наши коллекторы метрик для Zabbix, которые исторически имеют с коллекторами логов PostgreSQL общую архитектуру.
И правда, каждый объект мониторинга (хост) генерирует для zabbix практически стабильно один и тот набор метрик с одной и той же частотой все время:
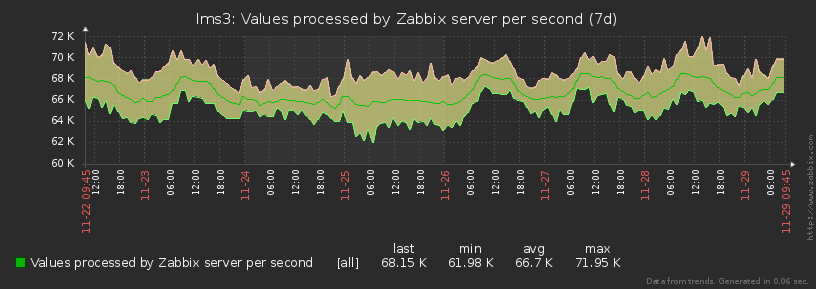
Как видно на графике, разница между min-max значениями количества генерируемых метрик не превышает 15%. Поэтому мы можем считать все объекты равными в одинаковых «попугаях».
Сильный «дисбаланс» между объектами
В отличие от предыдущей модели, для коллекторов логов наблюдаемые хосты совсем не являются однородными.
Например, один хост может генерировать в лог миллион планов за сутки, другой десятки тысяч, а какой-то — и вовсе единицы. Да и сами эти планы по объему и сложности и по распределению во времени суток сильно отличаются. Так и получается, что нагрузку сильно «качает», в разы:

Ну, а раз нагрузка может меняться настолько сильно, то надо учиться ей управлять…
Координатор
Сразу понимаем, что нам явно понадобится масштабирование системы коллекторов, поскольку один отдельный узел со всей нагрузкой когда-то точно перестанет справляться. А для этого нам потребуется координатор — тот, кто будет управлять всем зоопарком.
Получается примерно такая схема:

Каждый worker свою нагрузку «в попугаях» и в процентах CPU периодически сбрасывает master'у, те — коллектору. А он, на основании этих данных, может выдать команду типа «новый хост посадить на ненагруженный worker#4» или «hostA надо пересадить на worker#3».
Тут еще надо помнить, что, в отличие от объектов мониторинга, сами коллекторы имеют вовсе не равную «мощность» — например, на одном у вас может оказаться 8 ядер CPU, а на другом — только 4, да еще и меньшей частоты. И если нагрузить их задачами «поровну», то второй начнет «затыкаться», а первый — простаивать. Отсюда и вытекают…
Задачи координатора
По сути, задача всего одна — обеспечивать максимально равномерное распределение всей нагрузки (в %cpu) по всем доступным worker'ам. Если мы сможем решить ее идеально, то и равномерность распределения %cpu-нагрузки по коллекторам получим «автоматом».
Понятно, что, даже если каждый объект генерирует одинаковую нагрузку, со временем какие-то из них могут «отмирать», а какие-то возникать новые. Поэтому управлять всей ситуацией надо уметь динамически и поддерживать баланс постоянно.
Динамическая балансировка
Простую задачу (zabbix) мы можем решить достаточно банально:
- вычисляем относительную мощность каждого коллектора «в задачах»
- делим все задачи между ними пропорционально
- между worker'ами распределяем равномерно

Но что делать в случае «сильно неравных» объектов, как для коллектора логов?..
Оценка равномерности
Выше мы все время употребляли термин "максимально равномерное распределение", а как вообще можно формально сравнить два распределения, какое из них «равномернее»?
Для оценки равномерности в математике давно существует такая вещь как среднеквадратичное отклонение. Кому лениво вчитываться:
S[X] = sqrt( sum[ ( x - avg[X] ) ^ 2 of X ] / count[X] )Поскольку количество worker'ов на каждом из коллекторов у нас тоже может отличаться, то нормировать разброс по нагрузке надо не только между ними, но и между коллекторами в целом.
То есть распределение нагрузки по worker'ам двух коллекторов
[ (10%, 10%, 10%, 10%, 10%, 10%) ; (20%) ] — это тоже не очень хорошо, поскольку на первом получается 10%, а на втором — 20%, что как бы вдвое больше в относительных величинах.Поэтому введем единую метрику-расстояние для общей оценки «равномерности»:
d([%wrk], [%col]) = sqrt( S[%wrk] ^ 2 + S[%col] ^ 2 )Моделирование
Если бы объектов у нас было немного, то мы могли бы полным перебором «разложить» их между worker'ами так, чтобы метрика оказалась минимальной. Но объектов у нас — тысячи, поэтому такой способ не подойдет. Зато мы знаем, что коллектор умеет «перемещать» объект с одного worker'а на другой — давайте этот вариант и смоделируем, используя метод градиентного спуска.
Понятно, что «идеальный» минимум метрики мы так можем и не найти, но локальный — точно. Да и сама нагрузка может изменяться во времени настолько сильно, что искать за бесконечное время «идеал» абсолютно незачем.
То есть нам осталось всего лишь определить, какой объект и на какой worker эффективнее всего «переместить». И сделаем это банальным переборным моделированием:
- для каждой пары (целевой host, worker) моделируем перенос нагрузки
- нагрузку от host внутри исходного worker'а считаем пропорционально «попугаям»
В нашем случае за «попугая» оказалось вполне разумно взять объем получаемого потока логов в байтах. - относительную мощность между коллекторами считаем пропорциональной «суммарным попугаям»
- вычисляем метрику d для «перенесенного» состояния
Выстраиваем все пары по возрастанию метрики. В идеале, нам всегда стоит реализовать перенос именно первой пары, как дающий минимальную целевую метрику. К сожалению, в реальности сам процесс переноса «стоит ресурсов», поэтому не стоит запускать его для одного и того же объекта чаще определенного интервала «охлаждения».
В этом случае мы можем взять вторую, третью,… по рангу пару — лишь бы целевая метрика уменьшалась относительно текущего значения.
Если же уменьшать некуда — вот он локальный минимум!
Пример на картинке:

Запускать итерации «до упора» при этом вовсе не обязательно. Например, можно делать усредненный анализ нагрузки на интервале 1 мин, и по его завершению делать единственный перенос.
Микро-оптимизации
Понятно, что алгоритм со сложностью
T(целей) x W(процессов) — это не очень хорошо. Но в нем стоит не забыть применить некоторые более-менее очевидные оптимизации, которые его могут ускорить в разы.Нулевые «попугаи»
Если на замеренном интервале объект/задача/хост сгенерировал нагрузку «0 штук», то его не то что перемещать куда-то — его даже рассматривать и анализировать не надо.
Самоперенос
При генерации пар нет необходимости оценивать эффективность переноса объекта на тот же самый worker, где он и так находится. Все-таки уже будет
T x (W - 1) — мелочь, а приятно!Неразличимая нагрузка
Поскольку мы моделируем все-таки перенос именно нагрузки, а объект — всего лишь инструмент, то пробовать переносить «одинаковый» %cpu нет смысла — значения метрик останутся точно те же, хоть и для другого распределения объектов.
То есть достаточно оценить единственную модель для кортежа (wrkSrc, wrkDst, %cpu). Ну, а «одинаковыми» вы можете считать, например, значения %cpu, совпадающие до 1 знака после запятой.
Пример реализации на JavaScript
var col = {
'c1' : {
'wrk' : {
'w1' : {
'hst' : {
'h1' : 5
, 'h2' : 1
, 'h3' : 1
}
, 'cpu' : 80.0
}
, 'w2' : {
'hst' : {
'h4' : 1
, 'h5' : 1
, 'h6' : 1
}
, 'cpu' : 20.0
}
}
}
, 'c2' : {
'wrk' : {
'w1' : {
'hst' : {
'h7' : 1
, 'h8' : 2
}
, 'cpu' : 100.0
}
, 'w2' : {
'hst' : {
'h9' : 1
, 'hA' : 1
, 'hB' : 1
}
, 'cpu' : 50.0
}
}
}
};
// вычисляем опорные метрики и нормализуем по "мощности"
let $iv = (obj, fn) => Object.values(obj).forEach(fn);
let $mv = (obj, fn) => Object.values(obj).map(fn);
// initial reparse
for (const [cid, c] of Object.entries(col)) {
$iv(c.wrk, w => {
w.hst = Object.keys(w.hst).reduce((rv, hid) => {
if (typeof w.hst[hid] == 'object') {
rv[hid] = w.hst[hid];
return rv;
}
// нулевые значения ничего не решают, поэтому сразу отбрасываем
if (w.hst[hid]) {
rv[hid] = {'qty' : w.hst[hid]};
}
return rv;
}, {});
});
c.wrk = Object.keys(c.wrk).reduce((rv, wid) => {
// ID воркеров должны быть глобально-уникальны
rv[cid + ':' + wid] = c.wrk[wid];
return rv;
}, {});
}
// среднеквадратичное отклонение
let S = col => {
let wsum = 0
, wavg = 0
, wqty = 0
, csum = 0
, cavg = 0
, cqty = 0;
$iv(col, c => {
$iv(c.wrk, w => {
wsum += w.cpu;
wqty++;
});
csum += c.cpu;
cqty++;
});
wavg = wsum/wqty;
wsum = 0;
cavg = csum/cqty;
csum = 0;
$iv(col, c => {
$iv(c.wrk, w => {
wsum += (w.cpu - wavg) ** 2;
});
csum += (c.cpu - cavg) ** 2;
});
return [Math.sqrt(wsum/wqty), Math.sqrt(csum/cqty)];
};
// метрика-расстояние
let distS = S => Math.sqrt(S[0] ** 2 + S[1] ** 2);
// выбираем оптимальный перенос и моделируем его
let iterReOrder = col => {
let qty = 0
, max = 0;
$iv(col, c => {
c.qty = 0;
c.cpu = 0;
$iv(c.wrk, w => {
w.qty = 0;
$iv(w.hst, h => {
w.qty += h.qty;
});
w.max = w.qty * (100/w.cpu);
c.qty += w.qty;
c.cpu += w.cpu;
});
c.cpu = c.cpu/Object.keys(c.wrk).length;
c.max = c.qty * (100/c.cpu);
qty += c.qty;
max += c.max;
});
$iv(col, c => {
c.nrm = c.max/max;
$iv(c.wrk, w => {
$iv(w.hst, h => {
h.cpu = h.qty/w.qty * w.cpu;
h.nrm = h.cpu * c.nrm;
});
});
});
// "текущее" среднеквадратичное отклонение
console.log(S(col), distS(S(col)));
// формируем набор хостов и воркеров
let wrk = {};
let hst = {};
for (const [cid, c] of Object.entries(col)) {
for (const [wid, w] of Object.entries(c.wrk)) {
wrk[wid] = {
wid
, cid
, 'wrk' : w
, 'col' : c
};
for (const [hid, h] of Object.entries(w.hst)) {
hst[hid] = {
hid
, wid
, cid
, 'hst' : h
, 'wrk' : w
, 'col' : c
};
}
}
}
// реализация переноса нагрузки на целевой worker
let move = (col, hid, wid) => {
let w = wrk[wid]
, h = hst[hid];
let wsrc = col[h.cid].wrk[h.wid]
, wdst = col[w.cid].wrk[w.wid];
wsrc.cpu -= h.hst.cpu;
wsrc.qty -= h.hst.qty;
wdst.qty += h.hst.qty;
// перенос на другой коллектор с "процентованием" нагрузки на CPU
if (h.cid != w.cid) {
let csrc = col[h.cid]
, cdst = col[w.cid];
csrc.qty -= h.hst.qty;
csrc.cpu -= h.hst.cpu/Object.keys(csrc.wrk).length;
wsrc.hst[hid].cpu = h.hst.cpu * csrc.nrm/cdst.nrm;
cdst.qty += h.hst.qty;
cdst.cpu += h.hst.cpu/Object.keys(cdst.wrk).length;
}
wdst.cpu += wsrc.hst[hid].cpu;
wdst.hst[hid] = wsrc.hst[hid];
delete wsrc.hst[hid];
};
// моделирование и оценка переноса для пары (host, worker)
let moveCheck = (orig, hid, wid) => {
let w = wrk[wid]
, h = hst[hid];
// тот же воркер - ничего не делаем
if (h.wid == w.wid) {
return;
}
let col = JSON.parse(JSON.stringify(orig));
move(col, hid, wid);
return S(col);
};
// хэш уже проверенных переносов (hsrc,hdst,%cpu)
let checked = {};
// перебираем все возможные пары (какой хост -> на какой воркер)
let moveRanker = col => {
let currS = S(col);
let order = [];
for (hid in hst) {
for (wid in wrk) {
// нет смысла пробовать повторно перемещать одну и ту же (с точностью до 0.1%) "мощность" между одной парой воркеров
let widsrc = hst[hid].wid;
let idx = widsrc + '|' + wid + '|' + hst[hid].hst.cpu.toFixed(1);
if (idx in checked) {
continue;
}
let _S = moveCheck(col, hid, wid);
if (_S === undefined) {
_S = currS;
}
checked[idx] = {
hid
, wid
, S : _S
};
order.push(checked[idx]);
}
}
order.sort((x, y) => distS(x.S) - distS(y.S));
return order;
};
let currS = S(col);
let order = moveRanker(col);
let opt = order[0];
console.log('best move', opt);
// реализуем перенос
if (distS(opt.S) < distS(currS)) {
console.log('move!', opt.hid, opt.wid);
move(col, opt.hid, opt.wid);
console.log('after move', JSON.parse(JSON.stringify(col)));
return true;
}
else {
console.log('none!');
}
return false;
};
// пока есть что-куда переносить
while(iterReOrder(col));В результате, нагрузка по нашим коллекторам распределяется практически одинаково в каждый момент времени, оперативно нивелируя возникающие пики: