 Привет, Хаброжители! Нужно решить конкретную задачу, а перед вами куча непонятных данных, в которой черт ногу сломит? «Байесовская статистика» расскажет, как принимать правильные решения, задействуя свою интуицию и простую математику.
Привет, Хаброжители! Нужно решить конкретную задачу, а перед вами куча непонятных данных, в которой черт ногу сломит? «Байесовская статистика» расскажет, как принимать правильные решения, задействуя свою интуицию и простую математику.Пора забыть про заумные и занудные университетские лекции! Эта книга даст вам полное понимание байесовской статистики буквально «на пальцах» — с помощью простых объяснений и ярких примеров.
Чтобы узнать, как применить байесовские подходы к реальной жизни, вы отправитесь на охоту за НЛО, поиграете в «Лего», рассчитаете вероятность выживания Хана Соло при полете через поле астероидов, а также узнаете, как оценить вероятность того, что вы не заболели (ковидом?!), несмотря на то, что нагуглили все симптомы родильной горячки.
Прикладные задачи и упражнения помогут закрепить материал и заложить фундамент для работы с широким спектром задач: от невероятных текущих событий до ежедневных сюрпризов делового мира.
Вы научитесь:
- Работать с распределениями и неопределенностями.
- Сравнивать гипотезы и делать надежные выводы.
- Использовать теорему Байеса.
- Делать оценку апостериорной вероятности и проверять правильность собственных выводов.
Всегда выбирайте лучшее!
Байесовские априорные вероятности и распределение вероятностей
Априорные вероятности являются наиболее спорным аспектом теоремы Байеса, потому что их часто считают субъективными. Но на практике они нередко иллюстрируют, как применять жизненно важную справочную информацию, чтобы полностью обосновать неопределенную ситуацию.
В этой главе мы рассмотрим, как использовать априорные вероятности для решения проблемы, а также способы использования распределений вероятностей для численного описания наших убеждений как диапазона возможных значений, а не отдельных значений. Использование вероятностных распределений вместо отдельных значений полезно по двум основным причинам.
Во-первых, в действительности часто существует широкий спектр возможных убеждений, которые можно было бы иметь и рассматривать. Во-вторых, представление диапазонов вероятностей позволяет заявить об уверенности в ряде гипотез. Мы рассмотрели оба примера при изучении таинственной коробочки из главы 5.
Сомнения C-3PO насчет области астероидов
В качестве примера возьмем одну из самых запоминающихся ошибок статистического анализа из эпизода «Звездные войны: Империя наносит ответный удар». Когда Хан Соло, пытаясь уклониться от вражеских истребителей, направляет «Тысячелетний Сокол» в астероидное поле, всезнающий C-3PO сообщает Хану, что вероятность не на его стороне. C-3PO говорит: «Сэр, возможность успешного преодоления области астероидов — 3720 к 1!»
«Никогда больше не сообщай мне соотношение!» — отвечает Хан.
На первый взгляд, это просто забавный эпизод, в котором игнорируется «скучный» анализ данных, но на самом деле здесь присутствует интересная дилемма. Мы, зрители, знаем, что Хан справится с препятствием, но при этом с анализом C-3PO не согласиться не можем. Даже Хан считает, что это опасно, говоря: «Они, должно быть, сумасшедшие, раз последовали за нами». А еще ни один из преследующих бойцов TIE не проходит астероидную область, что является довольно убедительным доказательством того, что цифры C-3PO не лишены здравого смысла.
Однако C-3PO упускает из своих расчетов тот факт, что Хан — крутой сорвиголова! C-3PO не ошибается, он просто забывает добавить важную информацию. Теперь возникает вопрос: можем ли мы найти способ избежать ошибки C-3PO без полного исключения вероятности, как предлагает Хан? Чтобы ответить на этот вопрос, нужно смоделировать как мышление C-3PO, так и то, что мы думаем о Хане, а затем смешать эти модели, используя теорему Байеса.
Мы начнем с рассуждений C-3PO в следующем разделе, а затем разберемся с крутостью Хана.
Определение убеждений C-3PO
C-3PO не просто составляет цифры. Он свободно владеет более чем шестью миллионами форм общения, и для его поддержки требуется много данных. Поэтому можно предположить, что он владеет фактами, подтверждающими его заявление о шансах преодолеть астероиды «приблизительно 3720 к 1». Однако C-3PO предоставляет лишь приблизительные шансы, а значит, его данные дают достаточно информации только для того, чтобы предложить диапазон возможных коэффициентов успеха. Чтобы представить этот диапазон, нужно взглянуть на распределение утверждений относительно вероятности успеха, а не на одно значение, представляющее вероятность.
Для C-3PO единственным возможным результатом является успех или провал при перемещении по области астероидов. Мы определим различные возможные вероятности успеха, учитывая данные C-3PO и используя бета-распределение, о котором шла речь в главе 5. Бета-распределение правильно моделирует диапазон возможных вероятностей для события с учетом доступной информации о соотношении успехов и неудач.
Напомним, что бета-распределение имеет параметры α (количество наблюдаемых успехов) и β (количество наблюдаемых отказов):
P (КоэффициентУспеха | Успехи и Неудачи) = Beta(α, β).
Это распределение говорит, какие показатели успеха наиболее возможны с учетом предоставленных данных. Чтобы определить убеждения C-3PO, мы сделаем некоторые предположения о том, откуда берутся его данные. Допустим, у C-3PO есть записи о том, что два человека выжили в астероидной области, а 7440 человек завершили свое путешествие из-за впечатляющего взрыва! На рис. 9.1 показан график функции плотности вероятности, которая представляет убеждение C-3PO об истинном коэффициенте успеха.

Для любого обычного пилота, входящего в область астероидов, все выглядит плохо. В байесовских терминах оценка C-3PO истинной вероятности успеха с учетом наблюдаемых данных, 3720:1, является правдоподобностью, о которой говорилось в главе 8. Затем нужно определить априорную вероятность.
Расчеты для преследователей Хана
Проблема анализа C-3PO состоит в том, что его данные относятся ко всем пилотам, но Хан сильно отличается от среднего пилота. Если мы не сможем рассчитать крутость Хана, анализ будет сорван — не только потому, что Хан прошел через область астероидов, но и потому, что мы твердо верим, что он это сделает. Статистика — это инструмент, который развивает и организует наши рассуждения и представления о мире. Если статистический анализ не только противоречит рассуждениям и убеждениям, но и не может их изменить, тогда с ним что-то не так.
У нас есть априорное убеждение, что Хан пройдет через астероидную область, потому что до сих пор он смог пережить все невероятные ситуации. Легендарность Хана Соло заключается в том, что несмотря на малую вероятность выживания, он всегда добивается успеха.
Априорная вероятность часто очень противоречива для аналитиков данных вне байесовского анализа. Многие считают, что просто «придумать» априорную вероятность — это необъективно. Но эта сцена — предметная глава о том, почему отстранение от наших априорных убеждений еще более абсурдно. Представьте, что вы впервые смотрите «Империю». Вы доходите до этой сцены, и ваш друг говорит: «Что ж, Хану конец». Нет никаких шансов, что вы ему поверите. Помните, что C-3PO не совсем ошибается в том, насколько маловероятно выживание. Поэтому если ваш друг скажет: «Что ж, истребителям TIE конец», — вы, вероятно, рассмеетесь и согласитесь.
Сейчас есть множество причин полагать, что Хан выживет, но нет цифр, подтверждающих данное убеждение. Давайте попробуем собрать все вместе.
Начнем с какого-либо верхнего предела для крутости Хана. Если бы мы поверили, что Хан абсолютно не может умереть, фильм стал бы предсказуемым и скучным. С другой стороны, вера в то, что Хан пройдет астероидную область, сильнее, чем вера C-3PO в то, что он этого не сделает, поэтому предположим, что наша вера в то, что Хан выживет, составляет 20 000 к 1. На рис. 9.2 показано распределение для априорной вероятности того, что Хан сделает это.
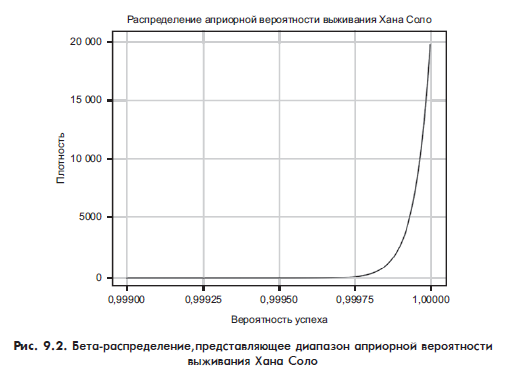
Это еще одно бета-распределение, которое используется по двум причинам. Во-первых, наши убеждения очень приблизительны, поэтому стоит признать переменный коэффициент успеха. Во-вторых, бета-распределение значительно облегчит будущие вычисления.
Теперь, учитывая правдоподобность и априорную вероятность, можно вычислить апостериорную вероятность в следующем разделе.
Создание неопределенности с апостериорной вероятностью
Мы установили, во что верит C-3PO (правдоподобность), и смоделировали наши собственные убеждения о Хане (априорная вероятность) — нужен способ объединить их. Объединяя убеждения, мы создаем апостериорное распределение. В этом случае апостериорная вероятность моделирует чувство неопределенности при изучении правдоподобности C-3PO: цель анализа C-3PO состоит в том, чтобы подшутить над его аналитическим мышлением, но также и создать ощущение реальной опасности. Одно только наше предварительное решение оставило бы нас совершенно безразличными к Хану, но после коррекции его на основе данных C-3PO мы развиваем новое убеждение, которое учитывает реальную опасность.
Формула для апостериорной вероятности на самом деле очень проста и интуитивно понятна. Учитывая, что у нас есть только правдоподобность и априорная вероятность, можно использовать пропорциональную форму теоремы Байеса, о которой говорилось в предыдущей главе:
Апостериорная вероятность ∝ Правдоподобность × Априорная вероятность.
Помните, что использование этой пропорциональной формы теоремы Байеса означает, что сумма апостериорных распределений необязательно равна 1. Но нам повезло, потому что есть простой способ объединить бета-распределения, которые дадут нормализованную апостериорную вероятность при наличии только правдоподобности и априорной вероятности. Таким образом, объединение двух бета-распределений — данные C-3PO (правдоподобность) и наше прежнее убеждение в способности Хана выжить в любой ситуации (априорная вероятность) — становится удивительно легким:
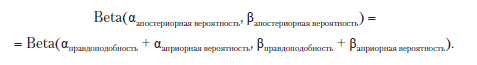
Мы просто добавляем альфы для априорной и апостериорной вероятностей и беты для априорной и апостериорной вероятностей — и получаем нормализованную апостериорную вероятность. Это просто, поэтому работа с бета-распределением очень удобна в байесовской статистике. Чтобы определить апостериорную вероятность для Хана, проходящего через область астероидов, мы можем выполнить этот простой расчет:
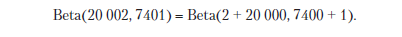
Теперь мы можем визуализировать новое распределение для наших данных. На рис. 9.3 показано последнее апостериорное убеждение.
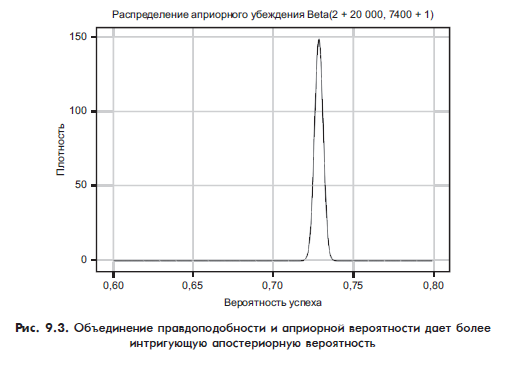
Объединив убеждения C-3PO с нашими убеждениями о преследователях Хана, мы получаем гораздо более разумную позицию. Наше апостериорное убеждение — шанс выживания примерно 73 %. Это значит, что Хан, скорее всего, выживет, однако мы все еще напряженно ждем развязки эпизода.
Действительно полезно, что у нас есть не просто грубая вероятность того, как Хан сможет это сделать, а скорее полное распределение возможных убеждений. Для многих примеров в книге мы придерживались простого использования единственного значения для вероятностей, но на практике использование полного распределения помогает проявлять гибкость относительно силы наших убеждений.
Заключение
В этой главе вы узнали, насколько важна исходная информация для анализа имеющихся данных. Данные C-3PO предоставили функцию правдоподобия, которая не соответствовала нашему априорному пониманию способностей Хана. Вместо того чтобы просто отклонить утверждение C-3PO, что делает Хан, мы объединили правдоподобность C-3PO с нашей априорной вероятностью, чтобы прийти к скорректированному убеждению о возможности успеха Хана. В эпизоде «Империя наносит ответный удар» эта неопределенность жизненно важна для напряженности, которую создает сцена. Если мы полностью поверим данным C-3PO или нашим собственным априорным убеждениям, то будем почти уверены, что Хан либо умрет, либо выживет.
Вы также видели, что можно использовать распределение вероятностей, а не одну вероятность, чтобы выразить диапазон возможных убеждений. В последующих главах эти распределения будут рассмотрены более подробно, чтобы мы могли изучить нюансы неопределенности убеждений.
Упражнения
Чтобы убедиться, что вы понимаете, как объединить априорные распределения вероятности и правдоподобность для получения точного апостериорного распределения, попробуйте ответить на эти вопросы.
- Ваш друг находит монетку, подбрасывает ее и получает шесть орлов подряд, а затем одну решку. Найдите бета-распределение, которое описывает этот случай. Используйте интегрирование, чтобы определить вероятность того, что истинная вероятность выпадения орла находится в диапазоне от 0,4 до 0,6. Это значит, что монетка является относительно честной.
- Придумайте априорную вероятность того, что монетка честная. Используйте бета-распределение таким образом, чтобы с вероятностью не менее 95 процентов истинная вероятность выпадения орла составляла от 0,4 до 0,6.
- Теперь посмотрите, сколько еще орлов (без решек) потребуется, чтобы убедить вас в существовании реальной вероятности того, что монетка нечестная. В этом случае наша вера в то, что вероятность нечестности монетки составляет от 0,4 до 0,6, падает ниже 0,5.
Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 25% по купону — Байес
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.