А вы любите шпаргалки? Мы обожаем и поэтому сегодня публикуем статью, в которой собрана вся самая главная информация о квантовых вычислениях. Мы собрали её из пяти статей по теме, которые вышли до этого. Но самое главное — это только шпаргалка, а не quick-guide для новичков. Новичкам советуем изучать все статьи целиком, ссылки есть в списке под катом!

Здесь приводится информация об основных состояниях, вентилях и матрицах, полезные математические формулы и другие сведения, которые уже появлялись в публикациях этой серии.
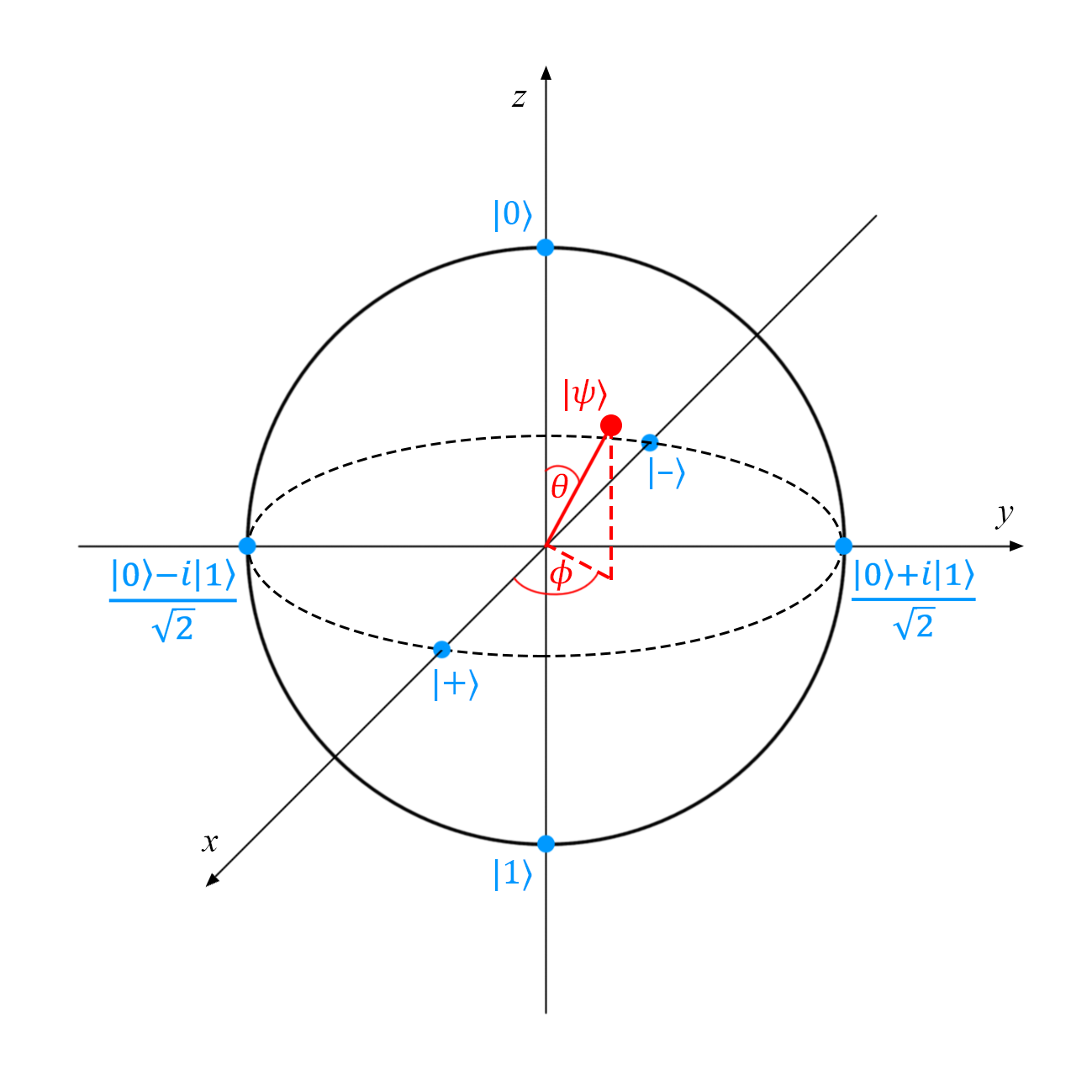
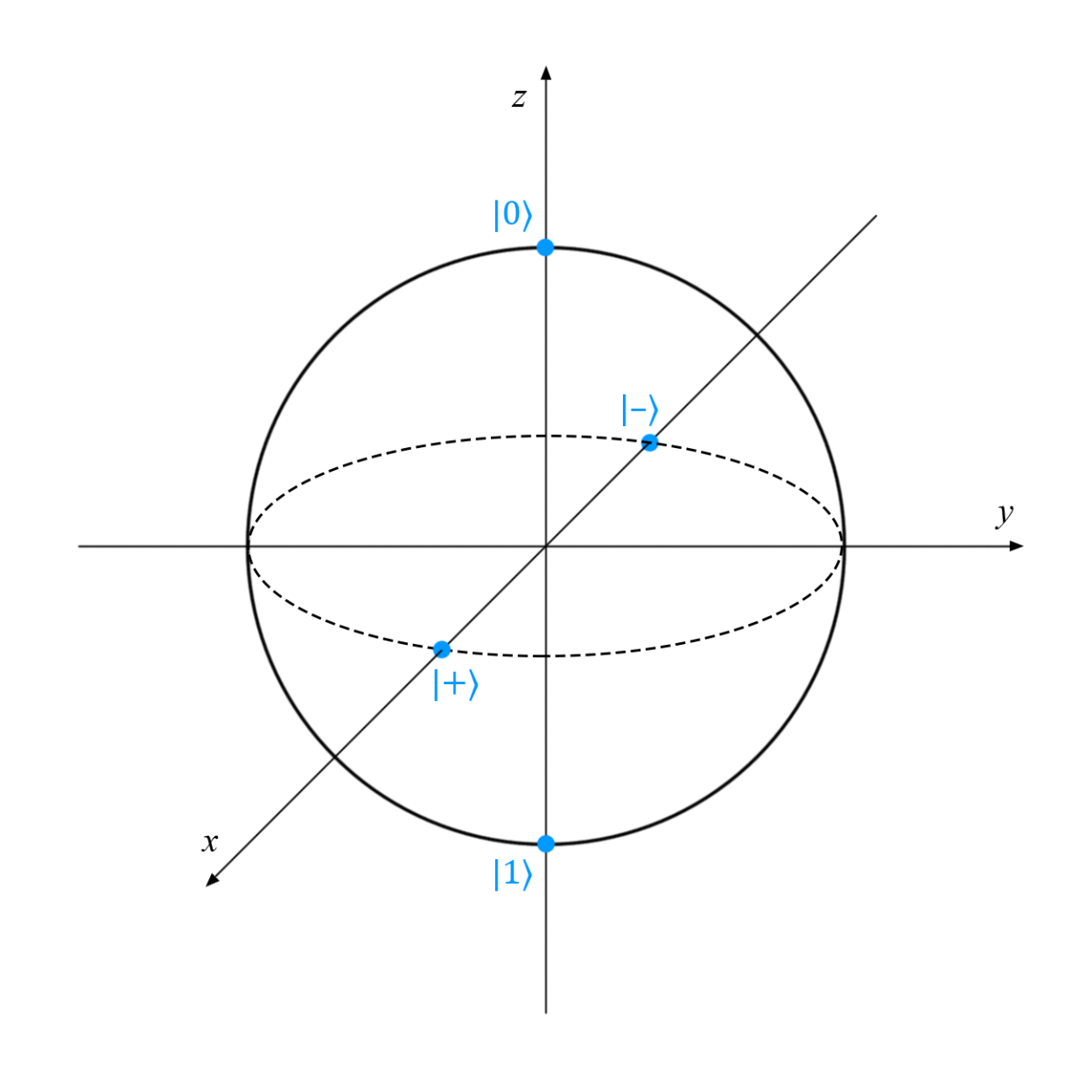
Любое унитарное преобразование вектора |ψ〉 можно наглядно представить в виде простого перемещения точки (отмеченной как |ψ〉) по сфере Блоха*. К сожалению, это наглядное представление подходит только для однокубитных состояний: простого обобщения для многокубитных систем пока не придумали. Сферу Блоха иногда называют единичной сферой.
*Чистым состояниям соответствуют точки на поверхности сферы, смешанным состояниям — точки внутри сферы. Подробное объяснение приводится в нашей публикации Основы квантовых вычислений: чистые и смешанные состояния.
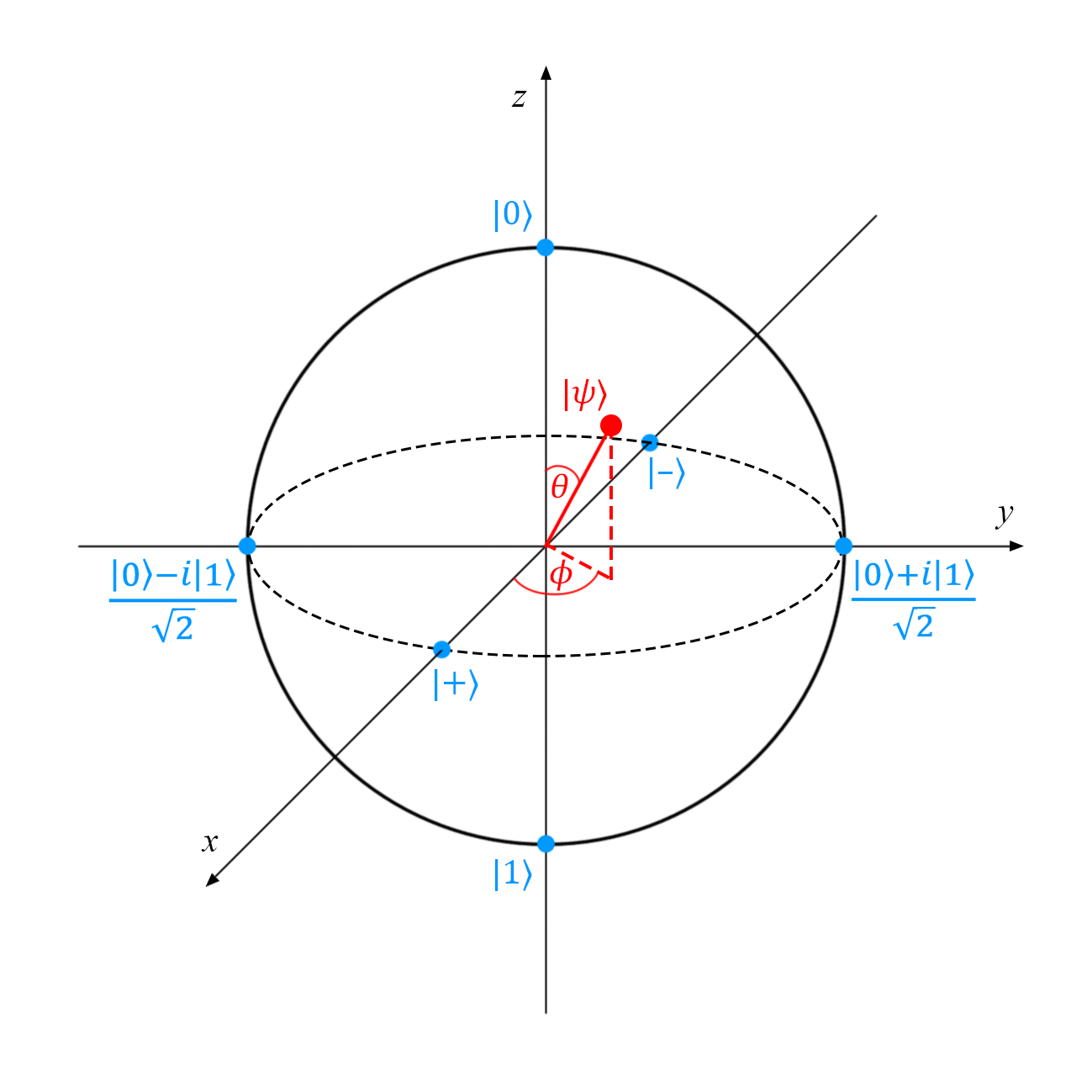
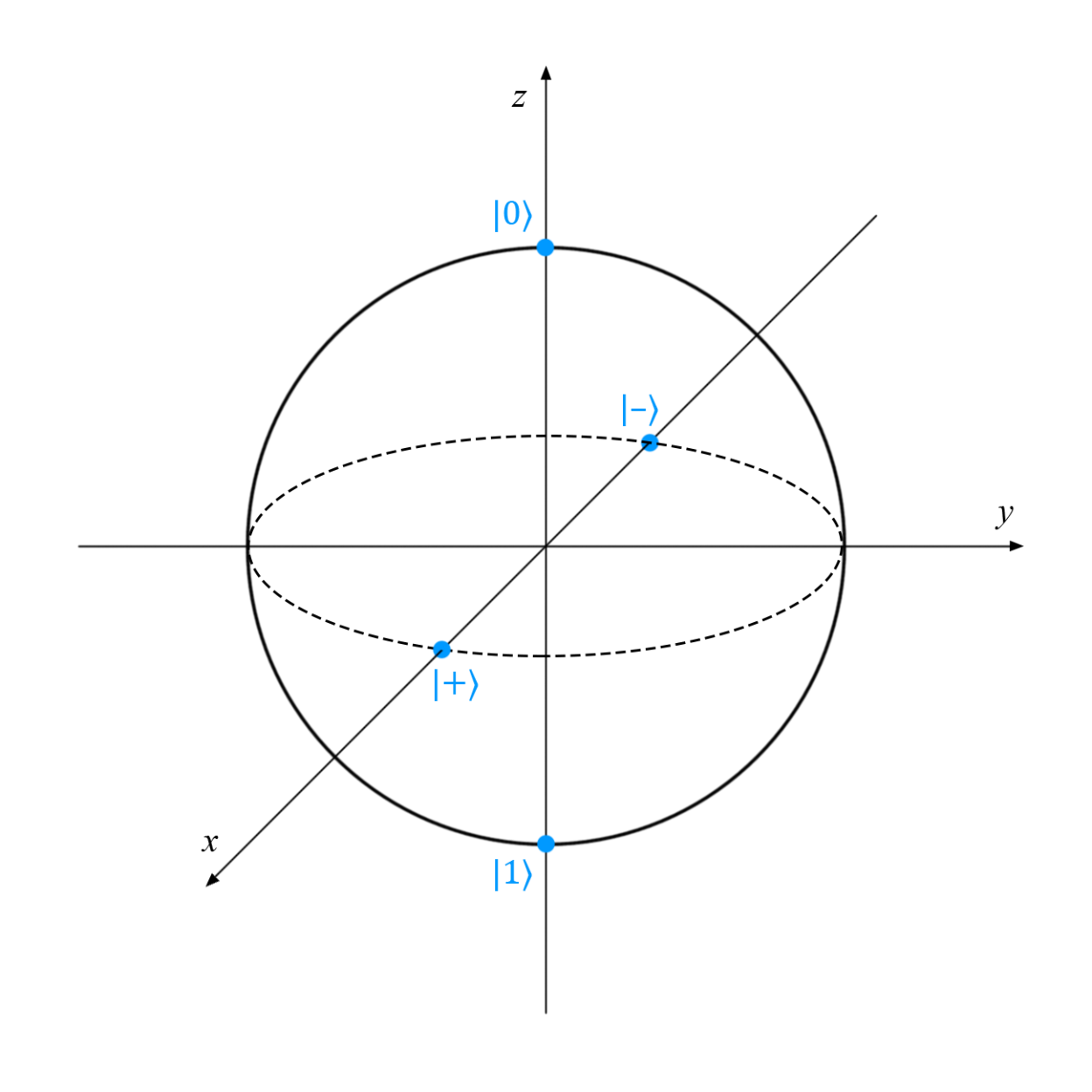
Однокубитные состояния
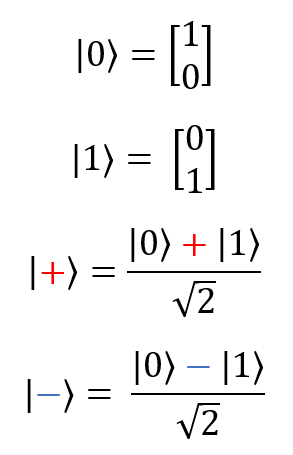
Состояния Белла (пары ЭПР) — простейшие примеры запутанных систем, состоящих из двух кубитов:
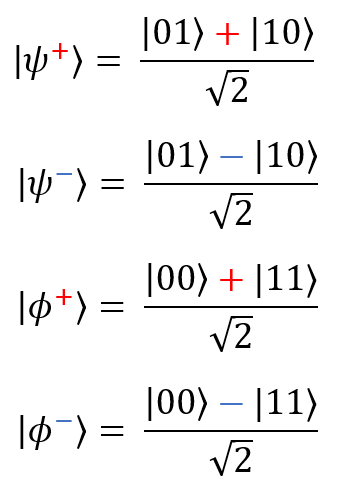
Состояния ГХЦ (Гринбергера — Хорна — Цайлингера) в общей форме (для n кубитов) и в простейшей форме (для трех кубитов):
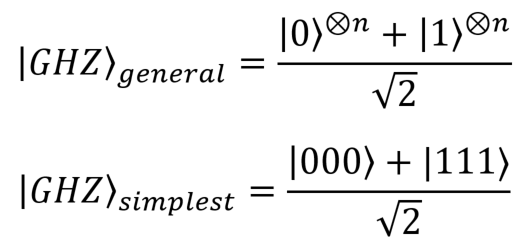
Ниже приводится краткая информация о важнейших вентилях, которые были представлены в нашей предыдущей публикации о вентилях и цепях. Мы добавили сведения об операциях для всех одно- и двухкубитных вентилей (если операций три и более, формулы становятся слишком длинными). В выражениях для управляемых вентилей единичная матрица (II) выделена красным, матрица исходного вентиля — синим, как в одной из предыдущих публикаций.
Матрицы Паули являются обратными сами к себе:
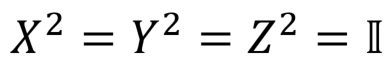
Оператор плотности можно определить как
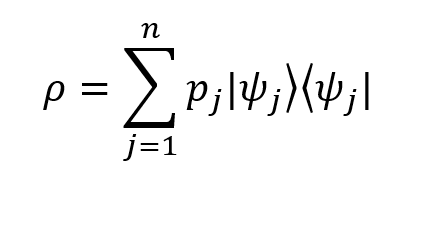
Здесь:

Статьи из цикла:
Здесь приводится информация об основных состояниях, вентилях и матрицах, полезные математические формулы и другие сведения, которые уже появлялись в публикациях этой серии.
Оглавление
- Сфера Блоха
- Основные квантовые состояния
- Вентили, матрицы и операции
- Полезные отношения и уравнения
Сфера Блоха
Любое унитарное преобразование вектора |ψ〉 можно наглядно представить в виде простого перемещения точки (отмеченной как |ψ〉) по сфере Блоха*. К сожалению, это наглядное представление подходит только для однокубитных состояний: простого обобщения для многокубитных систем пока не придумали. Сферу Блоха иногда называют единичной сферой.
*Чистым состояниям соответствуют точки на поверхности сферы, смешанным состояниям — точки внутри сферы. Подробное объяснение приводится в нашей публикации Основы квантовых вычислений: чистые и смешанные состояния.
Основные квантовые состояния
Однокубитные состояния

Состояния Белла (пары ЭПР) — простейшие примеры запутанных систем, состоящих из двух кубитов:
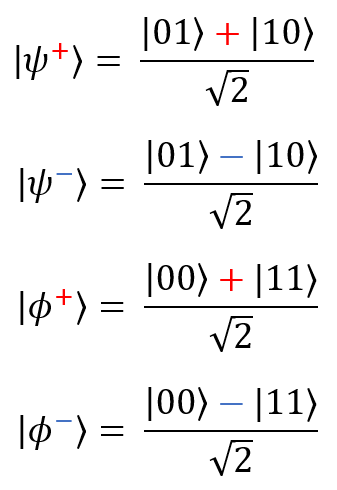
Состояния ГХЦ (Гринбергера — Хорна — Цайлингера) в общей форме (для n кубитов) и в простейшей форме (для трех кубитов):
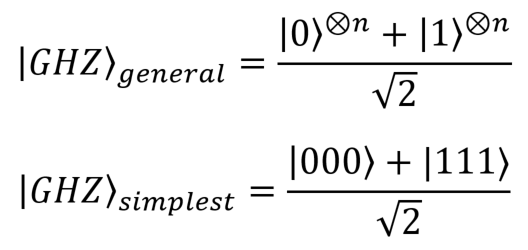
Вентили, матрицы и операции
Ниже приводится краткая информация о важнейших вентилях, которые были представлены в нашей предыдущей публикации о вентилях и цепях. Мы добавили сведения об операциях для всех одно- и двухкубитных вентилей (если операций три и более, формулы становятся слишком длинными). В выражениях для управляемых вентилей единичная матрица (II) выделена красным, матрица исходного вентиля — синим, как в одной из предыдущих публикаций.
| Названия | Матричное представление | Обозначения | Представление в Q# | Основные операции |
|---|---|---|---|---|
Вентиль Паули X, X, NOT, переключение бита, 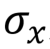 |
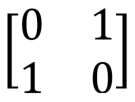 |
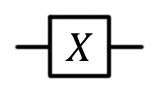 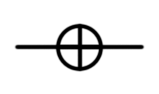 |
X(qubit: Qubit) | 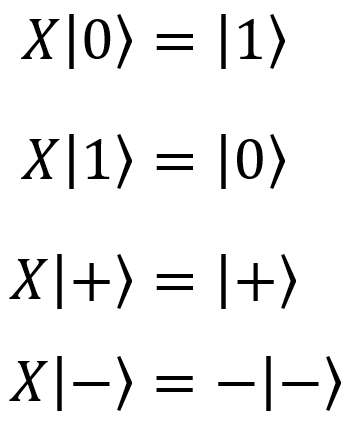 |
Вентиль Паули Y, Y, 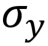 |
 |
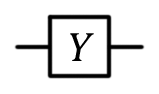 |
Y(qubit: Qubit) | 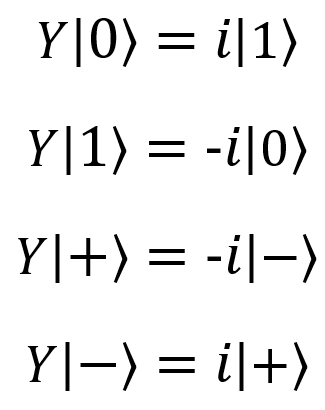 |
Вентиль Паули Z, Z, переключение фазы, 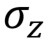 |
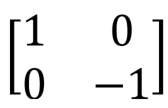 |
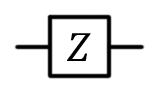 |
Z(qubit: Qubit) | 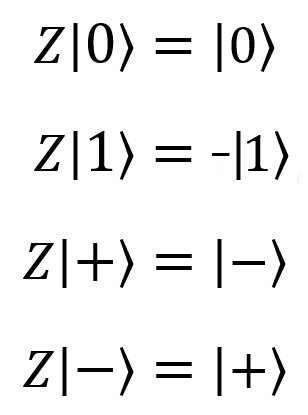 |
| Вентиль Адамара, H | 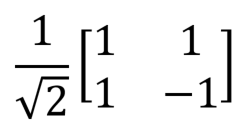 |
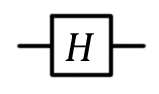 |
H(qubit: Qubit) | 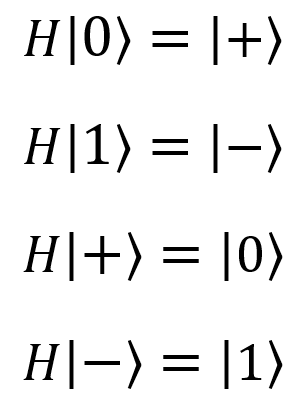 |
Фазовый сдвиг, 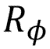 |
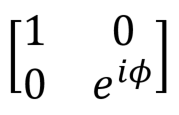 |
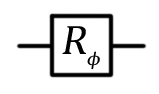 |
R1(theta: Double, qubit: Qubit) В более общем случае R(pauli: Pauli, theta: Double, qubit: Qubit) |
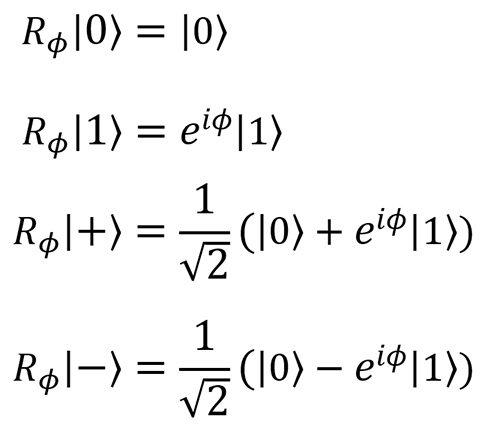 |
Фазовый сдвиг,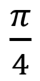 , S , S |
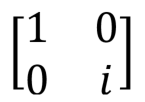 |
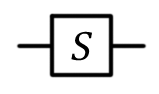 |
S(qubit: Qubit) | 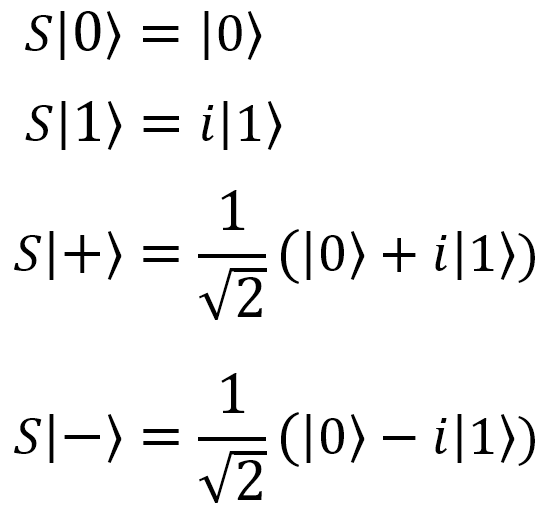 |
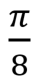 , T , T |
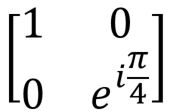 |
 |
T(qubit: Qubit) | 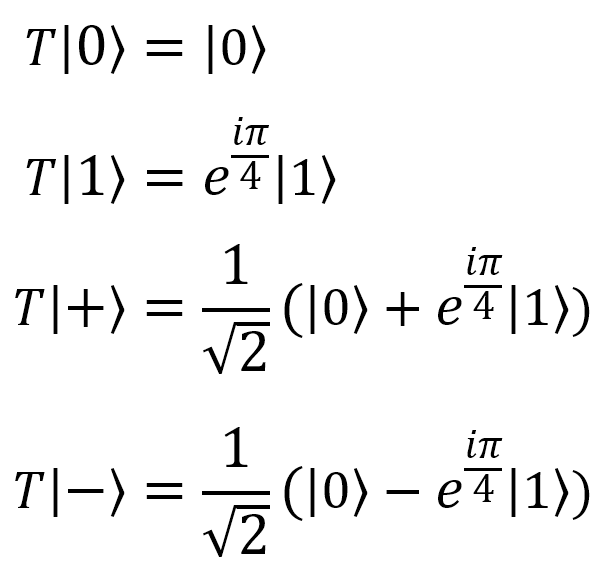 |
| SWAP | 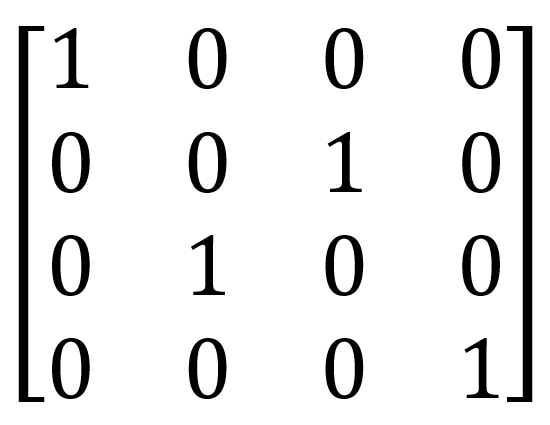 |
 |
SWAP(qubit1: Qubit, qubit2: Qubit) | 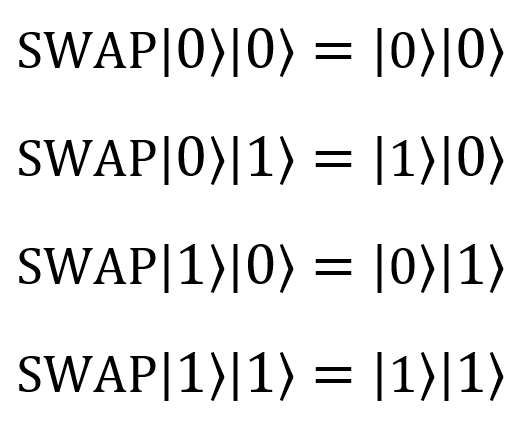 |
| CNOT |  |
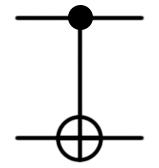 |
CNOT(control: Qubit, target: Qubit) или (Controlled X)([control], (target)); |
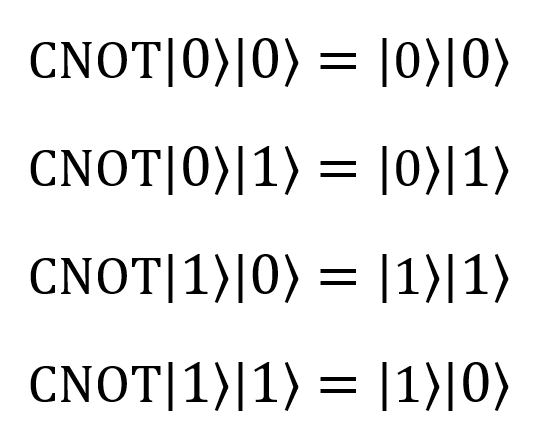 |
| CCNOT, вентиль Тоффоли |  |
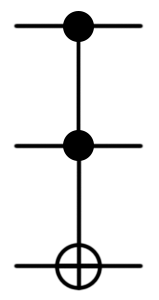 |
CCNOT(control1: Qubit, control2: Qubit, target: Qubit) или (Controlled X)([control1; control2], target); |
- |
| CSWAP, вентиль Фредкина |  |
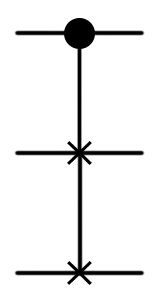 |
(Controlled SWAP)([control], (target)); | - |
Полезные отношения и уравнения
Матрицы Паули
Матрицы Паули являются обратными сами к себе:
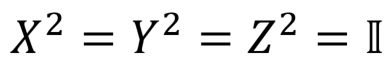
Оператор плотности
Оператор плотности можно определить как
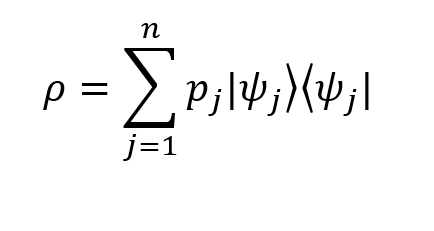
Здесь:
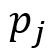 — вероятность того, что в начальный момент времени система находится в состоянии
— вероятность того, что в начальный момент времени система находится в состоянии 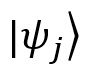 .
.- Элемент
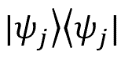 соответствует результату внешнего произведения вектора
соответствует результату внешнего произведения вектора 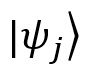 на себя (такое преобразование также называют оператором проектирования).
на себя (такое преобразование также называют оператором проектирования). - n — полное количество возможных состояний системы (в нашем примере их 3).
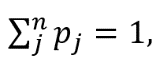 как и следовало ожидать (сумма вероятностей всех возможных состояний равна 1).
как и следовало ожидать (сумма вероятностей всех возможных состояний равна 1).
Ресурсы
- Более подробная информация доступна на веб-сайте Microsoft Quantum
- Загрузите Quantum Development Kit
- Подпишитесь на рассылку Microsoft Quantum
- Узнавайте о новейших разработках из блога Microsoft Quantum
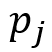 — вероятность того, что в начальный момент времени система находится в состоянии
— вероятность того, что в начальный момент времени система находится в состоянии 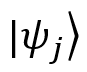 .
.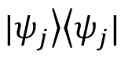 соответствует результату внешнего произведения вектора
соответствует результату внешнего произведения вектора 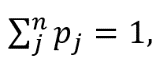 как и следовало ожидать (сумма вероятностей всех возможных состояний равна 1).
как и следовало ожидать (сумма вероятностей всех возможных состояний равна 1).