Комментарии 22
Отражение Пети находится для него внутри зеркала (судя по точке прохода сквозь плоскость зеркала), то есть Петя видит не только гостя, но и себя. Но нарисованная перспектива, на мой взгляд, противоречит такому раскладу.
А кто умеет аргументированно подсказать, может ли выделенная точка находиться там, где ее нарисовал автор?
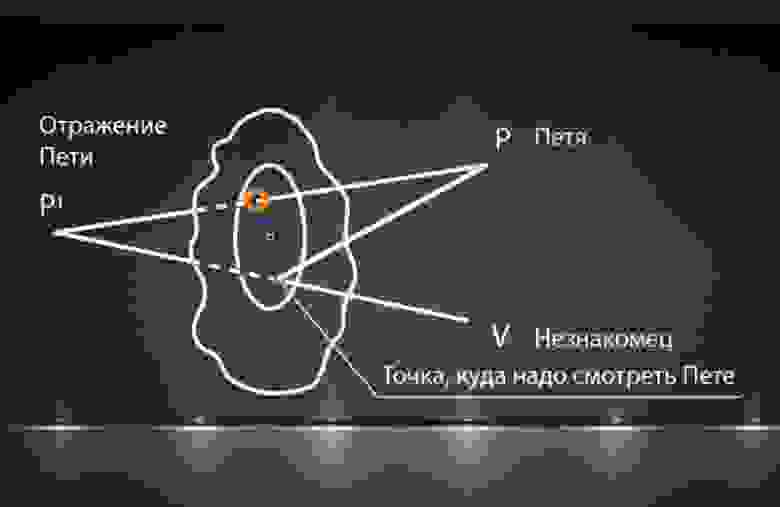
А кто умеет аргументированно подсказать, может ли выделенная точка находиться там, где ее нарисовал автор?
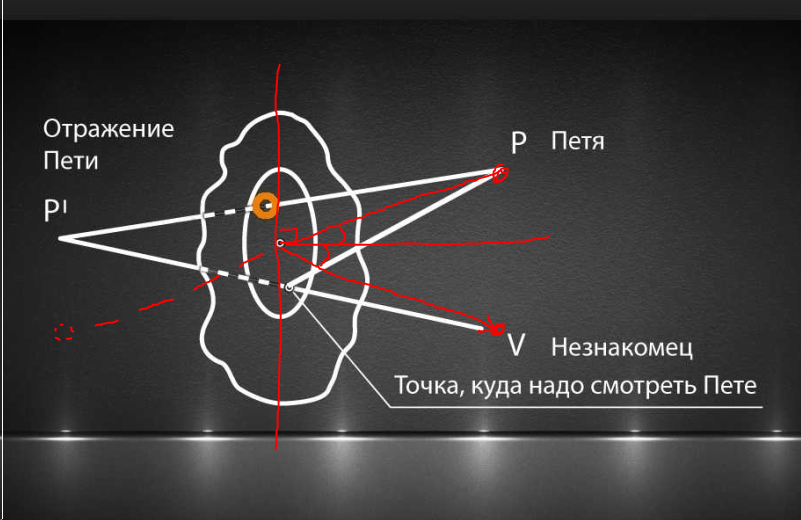
Почему нельзя смотреть вот так:
Потому что если автор просто запутался с перспективой, то вы ее совсем потеряли.
У меня по-прежнему стойкое ощущение, что на изначальном рисунке путают линзу и плоское зеркало.
Ничего никто не путает. Как вы будете искать в плоскости зеркала такую точку, чтобы угол падения был равен углу отражения, без дополнительных построений?
С дополнительными, но ради бога не с такими. На рисунке изначальном угол падения НЕ равен углу отражения.
Сначала рассмотрим двухмерный случай (повернём зеркало так, чтобы осталась только тонкая линия).
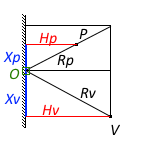
Пусть А = Xp+Xv. Пусть B = Xv:Xp = Rv:Rp = Hv:Hp (дважды теорема Фалеса). Решаем систему относительно Хр: Хр = А / (1+В)
Зная Хр легко выходим в точку О. Дальше достаточно проверить попадание этой точки в эллипс нашего зеркала.
Как прийти к этой картинке из трёхмерного случая? Вот так: провести плоскости, параллельные плоскости зеркала, через точки P и V (если это одна плоскость, задача вырождается в элементарную), после чего построить плоскость, перпендикулярную плоскости зеркала, содержащую оба перпендикуляра Нр и Hv.
Сначала рассмотрим двухмерный случай (повернём зеркало так, чтобы осталась только тонкая линия).
Пусть А = Xp+Xv. Пусть B = Xv:Xp = Rv:Rp = Hv:Hp (дважды теорема Фалеса). Решаем систему относительно Хр: Хр = А / (1+В)
Зная Хр легко выходим в точку О. Дальше достаточно проверить попадание этой точки в эллипс нашего зеркала.
Как прийти к этой картинке из трёхмерного случая? Вот так: провести плоскости, параллельные плоскости зеркала, через точки P и V (если это одна плоскость, задача вырождается в элементарную), после чего построить плоскость, перпендикулярную плоскости зеркала, содержащую оба перпендикуляра Нр и Hv.
PS. У меня почему-то стойкое ощущение, что на бумаге задачу решили все, а с программированием не справились те, кто не знал формул, позволяющих все те же действия проделать с конкретными трехмерными координатами. Ну, или в тестах попадались хардкорные ситуации с точкой на зеркале на расстоянии R±ε (погрешность плавающей точки) (я бы не делал таких тестов)
Хардкорных тестов не было, я проверял (у меня решение зашло без каких-либо «безопасных» сравнений чисел с плавающей точкой). Возможно на бумаге действительно задачу решили многие, однако посылка во время контеста была всего одна, и с ошибкой в формуле, а не в технике.
однако посылка во время контеста была всего одна
Прошу прощения, можете пояснить, что Вы имели в виду?
Из всех участников попытался решить только один, и у того – была ошибка в формуле?
Да, попытка решения задачи была всего одна, и она получила вердикт Wrong Answer на втором тесте.
Прошу прощения, насчет ошибки в формуле я вас дезинформировал, только что пересмотрел ту посылку. В решении используется двойной тернарный поиск точки, в которой углы падения и отражения будут равны. Как будет свободное время, я попытаюсь сдать эту задачу тем же способом (чтобы понять, что конкретно участник делал неправильно).
Прошу прощения, насчет ошибки в формуле я вас дезинформировал, только что пересмотрел ту посылку. В решении используется двойной тернарный поиск точки, в которой углы падения и отражения будут равны. Как будет свободное время, я попытаюсь сдать эту задачу тем же способом (чтобы понять, что конкретно участник делал неправильно).
Ваше решение абсолютно верно, и, прошу заметить, никак не противоречит авторскому. На вашем рисунке вы также просто нашли бы точку O просто ортогонально отражая точку P относительно плоскости зеркала (на вашем рисунке — относительно вертикальной прямой, содержащей зеркало) и пересекая плоскость зеркала с прямой, проходящей через отражение P и точку V.
Как правильно заметил mayorovp, пожалуй единственной проблемой оригинального рисунка состоит в том, что прямая P'P должна быть перпендикулярно прямой, содержащей бОльшие полуоси эллипса. Доказать корректность авторского подхода просто — так как прямая P'P перпендикулярна плоскости зеркала, она перпендикулярно любой прямой, лежащей в этой плоскости. А значит, P'P перпендикулярна прямой, проходящий через точки пересечения плоскости и прямых P'P и P'V. Из этого же следует (обозначив буквой C точку пересечения плоскости и прямой P'V), что углы между плоскостью и прямыми PC и CV равны. После этого останется только проверить, что точка С находится на зеркале. Перехода к планиметрии при таком подходе не требуется, и код программы получается очень короткий.
Как правильно заметил mayorovp, пожалуй единственной проблемой оригинального рисунка состоит в том, что прямая P'P должна быть перпендикулярно прямой, содержащей бОльшие полуоси эллипса. Доказать корректность авторского подхода просто — так как прямая P'P перпендикулярна плоскости зеркала, она перпендикулярно любой прямой, лежащей в этой плоскости. А значит, P'P перпендикулярна прямой, проходящий через точки пересечения плоскости и прямых P'P и P'V. Из этого же следует (обозначив буквой C точку пересечения плоскости и прямой P'V), что углы между плоскостью и прямыми PC и CV равны. После этого останется только проверить, что точка С находится на зеркале. Перехода к планиметрии при таком подходе не требуется, и код программы получается очень короткий.
Система координат на рисунке не задана — поэтому введем свою. Пусть плоскость проекции будет плоскостью ZOX — а за «глубину» отвечает ось OY.
На проекции большая ось эллипса вертикальна — значит, плоскость зеркала параллельна OZ. Но тогда нормаль к этой плоскости должна быть перпендикулярна OZ. Но такая прямая в проекции должна стать горизонтальной.
Следовательно, прямая PP1 должна быть строго горизонтальной, а не наклонной.
Эти рассуждения верны как для ортогональной проекции, так и для центральной.
На проекции большая ось эллипса вертикальна — значит, плоскость зеркала параллельна OZ. Но тогда нормаль к этой плоскости должна быть перпендикулярна OZ. Но такая прямая в проекции должна стать горизонтальной.
Следовательно, прямая PP1 должна быть строго горизонтальной, а не наклонной.
Эти рассуждения верны как для ортогональной проекции, так и для центральной.
Приглашаем на олимпиаду школьников из Беларуси, называем ее международной. Признак международной олимпиады — наличие школьников из по крайней мере двух стран, проверять тексты задач на ошибки уровня тся/ться для этого вовсе не обязательно. Мне вот интересно, откуда у неизвестных в олимпиадном программировании вузов такое стойкое желание организовать олимпиаду с как можно более громким названием?
В заочном туре участвовали ученики из 4 стран.
Спасибо за информацию, тексты проверим.
Спасибо за информацию, тексты проверим.
Стойкое желание вполне понятно, и, как мне кажется, вполне резонно — «неизвестному в олимпиадном программировании» вузу хочется стать более известным.
Я конечно необъективен, так как выпускник этого вуза, и олимпиадник, но все-таки считаю организацию олимпиады для школьников самым приличным способом повысить известность вуза в олимпиадном плане. Вуз принимает участие в олимпиадах, выходит в финал ACM ICPC, и тем временем остается не очень известным. Организует (ежегодно, хотя хотелось бы чаще) олимпиаду для школьников, школьники отзываются, приезжают, решают задачи, победители получают призы. Взамен ~100% участников этой олимпиады узнают про этот вуз, а какой-то, пусть маленький, процент, возможно рассмотрит этот вуз в качестве будущей альма матер. Не вижу подвоха, с моей точки зрения — это win-win.
Я конечно необъективен, так как выпускник этого вуза, и олимпиадник, но все-таки считаю организацию олимпиады для школьников самым приличным способом повысить известность вуза в олимпиадном плане. Вуз принимает участие в олимпиадах, выходит в финал ACM ICPC, и тем временем остается не очень известным. Организует (ежегодно, хотя хотелось бы чаще) олимпиаду для школьников, школьники отзываются, приезжают, решают задачи, победители получают призы. Взамен ~100% участников этой олимпиады узнают про этот вуз, а какой-то, пусть маленький, процент, возможно рассмотрит этот вуз в качестве будущей альма матер. Не вижу подвоха, с моей точки зрения — это win-win.
Зачем ехать на межнар не умея писать довольно простой перебор с комбинаторикой — мне не очень понятно, но это не важно. Попасть на финал из неизвестного вуза довольно легко и я слышал об энтузиастах, которые поступают в неизвестный вуз, чтобы проделать этот трюк.
МАИ, например, довольно часто светится, выставляет стабильно много команд и некоторые добиваются довольно серьезных успехов, но что-то я никогда не слышал, чтобы МАИ организовывала открытые олимпиады для школьников. Но это тоже неважно.
Называть олимпиаду международной можно только формально и инициатива выглядит, как попытка косить под почти идентично зовущийся IOI, в которой уровень слова «международный» совершенно иной. Но это тоже неважно.
Что важно — так это отношение организаторов. Глупые орфографические ошибки в условиях; картинки, которые даже на хабре всех путают, закрытые задачи и результаты; список победителей лежит на бывшей странице регистрации и у нее все еще неверный заголовок, призеров называют победителями, победителей — призерами и не дают им диплом первой степени, как это обычно принято; олимпиада не ориентирована на уровень ниже, чем у московских спецшкол, но серебряный призер IOI все равно участвует и еще миллион мелочей, явно показывающий, что на образовательные и рекламные цели олимпиады всем пофиг, а людей с прямыми руками, которые могут сделать все по-нормальному в вузе нет совсем.
Все это очень напоминает воронежскую олимпиаду: esci.ru/ttb/vserossiyskaya_studencheskaya_olympiada_in_informatics.htm. Когда я был школьником, я прочитал этот текст и точно знал, в какой вуз я никогда не пойду даже заглянуть внутрь.
МАИ, например, довольно часто светится, выставляет стабильно много команд и некоторые добиваются довольно серьезных успехов, но что-то я никогда не слышал, чтобы МАИ организовывала открытые олимпиады для школьников. Но это тоже неважно.
Называть олимпиаду международной можно только формально и инициатива выглядит, как попытка косить под почти идентично зовущийся IOI, в которой уровень слова «международный» совершенно иной. Но это тоже неважно.
Что важно — так это отношение организаторов. Глупые орфографические ошибки в условиях; картинки, которые даже на хабре всех путают, закрытые задачи и результаты; список победителей лежит на бывшей странице регистрации и у нее все еще неверный заголовок, призеров называют победителями, победителей — призерами и не дают им диплом первой степени, как это обычно принято; олимпиада не ориентирована на уровень ниже, чем у московских спецшкол, но серебряный призер IOI все равно участвует и еще миллион мелочей, явно показывающий, что на образовательные и рекламные цели олимпиады всем пофиг, а людей с прямыми руками, которые могут сделать все по-нормальному в вузе нет совсем.
Все это очень напоминает воронежскую олимпиаду: esci.ru/ttb/vserossiyskaya_studencheskaya_olympiada_in_informatics.htm. Когда я был школьником, я прочитал этот текст и точно знал, в какой вуз я никогда не пойду даже заглянуть внутрь.
На удивление, участники плохо справились с задачами на геометрию.
Видимо вы не много соревнований провели. Иначе не удивлялись бы. Это вполне обычная картина.
Я не понимаю, откуда такое мнение. 70% задач на геометрию — тупые построения, как обе задачи из этой темы. Из оставшихся задач 95% решаются сканлайном либо выпуклой оболочкой. Оставшиеся задачи используют геометрические примитивы только для формулировки: они либо основаны на вытаскивании чисел и запихивании их в структуру данных, либо очень технические и не требуют думать, а просто аккуратно реализовать 9000 шагов, описанных в условии. Последние тяжело назвать геометрическими, это все равно что считать задачи с домами задачами на архитектуру. Это все дополняется тем, что ответ часто дробный и можно одним тестом проверить весь код сразу с очень неплохим шансом. Если задачи на геометрию решаются плохо — обычно это значит, что кто-то перегробил геометрию в туре.
Во-первых, да. Из геометрии легко сделать гроб, за который никто не возьмётся.
Во-вторых, частные случаи, которые не сразу можно заметить и из-за которых сдача затягивается на несколько попыток.
В третьих, тупые построения вместе с частными случаями требуют довольно много кода и тестирования, из-за чего геометрия откладывается на потом.
Отсюда и получается, что в таблице на месте геометрических задач либо прочерки, либо периодические "-12", "-23", сменяющие "+2", "+3"… :)
Во-вторых, частные случаи, которые не сразу можно заметить и из-за которых сдача затягивается на несколько попыток.
В третьих, тупые построения вместе с частными случаями требуют довольно много кода и тестирования, из-за чего геометрия откладывается на потом.
Отсюда и получается, что в таблице на месте геометрических задач либо прочерки, либо периодические "-12", "-23", сменяющие "+2", "+3"… :)
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Подведены итоги Олимпиады по программированию среди школьников