Знакомые с нейронными сетями читатели скорее всего слышали про термин «функция активации». Такие варианты функции активации, как сигмоида, гиперболический тангенс (TanH) и ReLU (линейный выпрямитель), активно применяются в нейронных сетях и широко известны энтузиастам, занимающимся экспериментами с нейронными архитектурами. Исследователи нейронных сетей не останавливаются на достигнутом и подбирают альтернативы, позволяющие расширить границы возможностей. Один из вариантов подхода, предложенного в 2020 году, показывает выдающиеся результаты по сравнению с классическими функциями активации. Про впечатляющие отличия и пойдет речь в этой статье: на основе материала Vincent Sitzmann, Julien N. P. Martel, Alexander Bergman, David B. Lindell, Gordon Wetzstein и кода на нескольких наглядных примерах будет продемонстрировано превосходство нового метода.

Для работы с сигналами можно использовать различные формы их представления. Простой пример — сигнал в форме таблицы, где для каждого временного шага имеется определенное значение переменной (температуры или др.). Такой сигнал будет представлен в дискретной форме, что в ряде случаев неудобно (так, при воспроизведении звука необходимо перейти от дискретного представления к непрерывному). Другой формой представления сигнала может быть заданная функция зависимости переменной f от времени t, тогда можно говорить о функции f(t). Такая форма представления сигнала имеет ряд преимуществ, например, возможность экстраполяции. Сигнал, разложенный на ряд Фурье, также представляет из себя удобную форму, позволяющую рассчитать спектр мощности, выделить характерные частоты и др. Интересно, что нейронная сеть также является формой представления сигнала, и свойства такого представления напрямую связаны с функцией активации нейронов.
У функции активации есть ряд желательных свойств, которые позволяют расширить возможности использования нейронных сетей. Например, крайне желательна нелинейность функции активации, т.к. в этом случае можно доказать, что двухуровневая нейронная сеть будет универсальным аппроксиматором функции. Другое желательное свойство — непрерывная дифференцируемость для обеспечения методов оптимизации на основе градиентного спуска. При этом популярная функция RELU не является непрерывно дифференцируемой и имеет проблемы с оптимизацией на основе градиентного спуска. Еще одно полезное свойство — возможность аппроксимации тождественной функции около начала координат. Если функции активации имеют это свойство, то нейронная сеть будет обучаться эффективно в случае инициализации весов малыми случайными значениями. Если функция активации не аппроксимирует тождество около начала координат, то приходится быть осторожными при инициализации весов.
Для использования синусоидальной функции активации получаем следующую формулу:

Здесь φi: RMi → RNi обозначает i-ый слой сети, Wi ∈ R Ni×Mi представляет собой матрицу весов, ответственную за аффинные преобразования сигнала, а bi ∈ RNi представляет собой смещение к вектору xi ∈ RMi
Интересно, что производная от предложенной функции активации также является синусоидальной функцией, т.к. производная от функции синуса является функция косинуса, которая в свою очередь является сдвинутой по фазе функцией синуса. Кроме того, синусоидальная функция активации позволяет аппроксимировать тождественную функцию около начала координат.
Таким образом, синусоидальная функция активации обладает рядом полезных свойств, таких, как нелинейность, непрерывная дифференцируемость и возможность аппроксимации тождественной функции около начала координат. Теперь давайте перейдем к теме статьи Vincent Sitzmann, Julien N. P. Martel, Alexander Bergman, David B. Lindell, Gordon Wetzstein.
Слабой стороной современных нейронных сетей является неспособность моделировать сигналы с мелкими деталями. Кроме того, современные нейронные сети не могут представлять пространственные и временные производные сигнала, что ограничивает возможности для их применения в физическом моделировании: производные оказывается важным элементом, неявно определенным через уравнения в частных производных, описывающих физические процессы.
Форма представления сигнала, параметризованная с помощью нейронной сети, и обладающая свойствами неявного определения, непрерывности и дифференцируемости, представляет собой отдельное направление в развитии нейронных архитектур. Такой подход способен предложить ряд преимуществ по сравнению с традиционными представлениями и поэтому может быть выделен в отдельную парадигму. Авторы статьи, в рамках новой парадигмы, предлагают использовать функции периодической активации для неявных нейронных представлений. Новый подход, под названием Сети Синусоидального Представления (sinusoidal representation networks) или SIREN, в работе авторов демонстрирует впечатляющие результаты в приложении к сложным сигналам физической природы и их производным.
В основной работе авторы анализируют статистические свойства активации SIREN, чтобы предложить принципиальную новую схему задания начальных значений для весов сети, и демонстрируют работу с изображениями, волновыми полями, видео, звуком и их производными. Далее авторы показывают, как можно использовать SIREN для решения сложных краевых задач, таких, как точное уравнение Эйконала (с получением функций расстояния со знаком), уравнение Пуассона, а также уравнения Гельмгольца и уравнения волнового движения. Наконец, авторы в своей статье объединили SIREN с гиперсетями для изучения априорных вероятностей в пространстве функций SIREN, однако этот материал уже выходит за рамки нашего обзора.
Следующие результаты сравнивают SIREN с различными сетевыми архитектурами. TanH, ReLU, Softplus и т. д. означает Multi Layer Perceptron одинакового размера с соответствующей функцией нелинейности. Авторы также сравнивают недавно предложенное позиционное кодирование (Partial Encoding) в сочетании с нелинейной функцией активации ReLU, обозначенной, как ReLU P.E. SIREN существенно превосходит все baseline результаты, сходится значительно быстрее и является единственной архитектурой, точно отражающей градиенты сигнала, позволяя тем самым использование в решении краевых задач.
SIREN, отображающая координаты 2D-пикселей в цвета, может быть использована для параметризации изображений. В данном случае авторы напрямую активируют SIREN, используя истинные значения пикселей. В данных примерах SIREN удается успешно аппроксимировать изображение, получая на 10 дБ более высокое значение PSNR в условиях меньшего количества итераций по сравнению с конкурентами. Кроме того, SIREN является единственным представителем Multi Layer Perceptron, которому удается точно отразить производные первого и второго порядка.
(код взят из https://colab.research.google.com/github/vsitzmann/siren/blob/master/explore_siren.ipynb)
Для начала, импортируем библиотеки и добавим вспомогательную функцию для визуализации
Теперь добавим реализацию синусоидального слоя, который будет основным строительным блоком SIREN. В данном случае используется гораздо более лаконичная реализация, чем в основном коде авторов, однако упрощение оправдано тем, что здесь не преследуется цель сравнения с baseline решениями.
И, наконец, дифференциальные операторы, которые позволяют использовать
Для экспериментов используется классическое изображение оператора.
Далее просто «фитируем» это изображение. В процессе аппроксимации мы стремимся параметризовать изображение f(x) в оттенках серого с пиксельными координатами x с помощью функции Φ(x). То есть мы ищем функцию Φ такую, что функционал L = ∫Ω∥Φ(x) − f(x)∥dx минимизируется. При этом Ω является областью изображения. Используем небольшой датасет, который вычисляет попиксельные координаты:
Далее создадим экземпляр датасета и SIREN. Поскольку пиксельные координаты являются двумерным вектором, SIREN получает на вход два признака, а поскольку изображение в оттенках серого, размерность выходного канала равна 1.
Теперь обучаем нейронную сеть в простом цикле. Всего за несколько сотен итераций хорошо аппроксимируются как изображение, так и его градиенты.




Начнем с небольшого эксперимента.
Будем использовать SIREN для параметризации аудиосигнала, то есть стремимся параметризовать звуковую волну f(t) в моменты времени t с помощью функции Φ. Для этого ищем функцию Φ такую, что: функция потерь L = ∫Ω∥Φ(t) −f(t)∥dt минимизируется, где Ω является звуковой волной. Для эксперимента будем использовать сонату Баха:
Создадим небольшой датасет, который позволяет перевести аудиофайл в более удобный для работы формат:
Далее создадим экземпляр SIREN. Поскольку звуковой сигнал имеет гораздо более высокую пространственную частоту в диапазоне от -1 до 1, поэтому увеличиваем ω0 в первом слое SIREN.
Давайте прослушаем исходные данные:
Далее начнем обучение нейронной сети:


Послушаем, что получается в итоге:
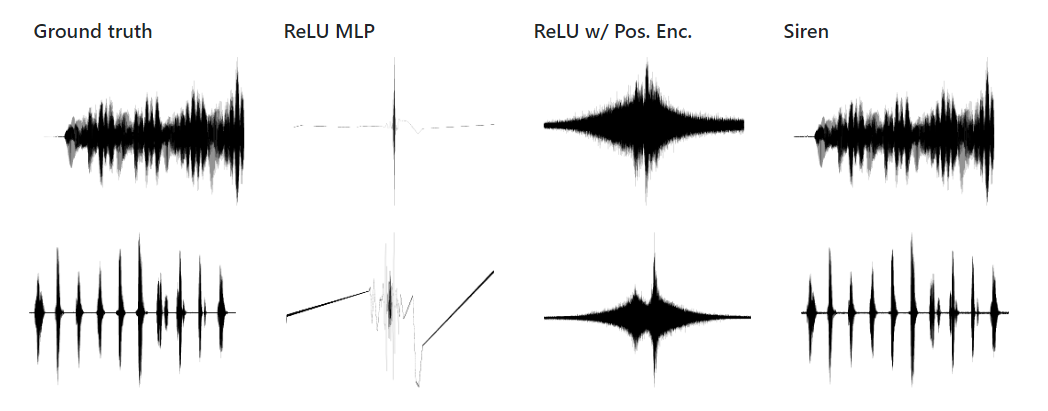
SIREN с одиночным входом, соответствующим координате времени, и скалярным выходом действительно может успешно параметризировать аудиосигналы. SIREN — единственная сетевая архитектура, которая успешно воспроизводит аудиосигнал как для музыки, так и для человеческого голоса.
Использование SIREN совместно на координатах пикселей и времени позволяет параметризовать видео. В данном случае SIREN непосредственно активируется на истинных значениях пикселей и позволяет параметризовать видео существенно лучше, чем ReLU Multi Layer Perceptron.

Используя только производные в подходе SIREN, возможно решить уравнение Пуассона. SIREN — это опять-таки единственная архитектура, которая аппроксимирует изображения, градиенты и области лапласиан точно и быстро.
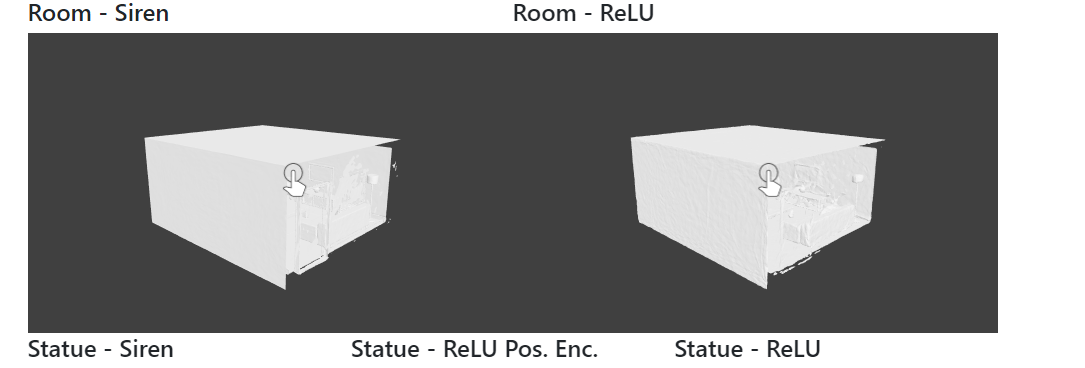
Решая краевую задачу в форме уравнений Эйконала, мы можем восстановить SDF из облака точек и нормалей поверхности. Подход SIREN позволяет восстановить сцену масштаба комнаты на основе только облака точек и нормалей поверхности, при этом удается точно воспроизвести мелкие детали, а для обучения требуется менее одного часа. В отличие от недавних работ по объединению воксельных сеток с нейронными неявными представлениями, в предлагаемом подходе полное представление хранится в весах одной пятислойной нейронной сети, без 2D или 3D-сверток, и поэтому требует гораздо меньшего количества параметров. Важно обратить внимание на то, что полученные SDF не обучаются на исходных значениях SDF, а скорее являются результатом решения вышеупомянутой эйкональной краевой задачи. Такая постановка задачи является существенно более сложной и требует обучения с учителем по градиентам (детали — в статье). В результате архитектуры сетей, градиенты которых хуже контролируются, показывают качество ниже, чем в подходе SIREN.

В данном случае авторы используют подход SIREN для решения неоднородного уравнения Гельмгольца. Архитектуры на основе ReLU и Tanh не позволяют полностью решить эту задачу.
При работе со временем, подход SIREN позволяет успешно решить волновое уравнение, в отличие от архитектуры на основе Tanh, которая не смогла сойтись к правильному решению.
Предлагаемое авторами представление SIREN для глубокого обучения помогает в работе с такими данными, как изображения, аудио- и видеосигналы. Новый подход может быть полезным в таких областях, как классификация изображений или speech-to-text в рамках работы со звуком. За счет больших возможностей SIREN по точному воспроизведению сигнала, а также градиентов и лапласианов можно ожидать, что генеративные модели с использованием SIREN смогут совершить качественный скачок в своих возможностях.
В данный момент мы рассматриваем возможности проверить SIREN на наших задачах в Центре компетенции больших данных и искусственного интеллекта ЛАНИТ. Хочется надеяться, что предлагаемый подход покажет свою продуктивность не только на простых примерах, но и на нетривиальных прикладных задачах.

Для работы с сигналами можно использовать различные формы их представления. Простой пример — сигнал в форме таблицы, где для каждого временного шага имеется определенное значение переменной (температуры или др.). Такой сигнал будет представлен в дискретной форме, что в ряде случаев неудобно (так, при воспроизведении звука необходимо перейти от дискретного представления к непрерывному). Другой формой представления сигнала может быть заданная функция зависимости переменной f от времени t, тогда можно говорить о функции f(t). Такая форма представления сигнала имеет ряд преимуществ, например, возможность экстраполяции. Сигнал, разложенный на ряд Фурье, также представляет из себя удобную форму, позволяющую рассчитать спектр мощности, выделить характерные частоты и др. Интересно, что нейронная сеть также является формой представления сигнала, и свойства такого представления напрямую связаны с функцией активации нейронов.
У функции активации есть ряд желательных свойств, которые позволяют расширить возможности использования нейронных сетей. Например, крайне желательна нелинейность функции активации, т.к. в этом случае можно доказать, что двухуровневая нейронная сеть будет универсальным аппроксиматором функции. Другое желательное свойство — непрерывная дифференцируемость для обеспечения методов оптимизации на основе градиентного спуска. При этом популярная функция RELU не является непрерывно дифференцируемой и имеет проблемы с оптимизацией на основе градиентного спуска. Еще одно полезное свойство — возможность аппроксимации тождественной функции около начала координат. Если функции активации имеют это свойство, то нейронная сеть будет обучаться эффективно в случае инициализации весов малыми случайными значениями. Если функция активации не аппроксимирует тождество около начала координат, то приходится быть осторожными при инициализации весов.
Для использования синусоидальной функции активации получаем следующую формулу:
Здесь φi: RMi → RNi обозначает i-ый слой сети, Wi ∈ R Ni×Mi представляет собой матрицу весов, ответственную за аффинные преобразования сигнала, а bi ∈ RNi представляет собой смещение к вектору xi ∈ RMi
Интересно, что производная от предложенной функции активации также является синусоидальной функцией, т.к. производная от функции синуса является функция косинуса, которая в свою очередь является сдвинутой по фазе функцией синуса. Кроме того, синусоидальная функция активации позволяет аппроксимировать тождественную функцию около начала координат.
Таким образом, синусоидальная функция активации обладает рядом полезных свойств, таких, как нелинейность, непрерывная дифференцируемость и возможность аппроксимации тождественной функции около начала координат. Теперь давайте перейдем к теме статьи Vincent Sitzmann, Julien N. P. Martel, Alexander Bergman, David B. Lindell, Gordon Wetzstein.
Слабой стороной современных нейронных сетей является неспособность моделировать сигналы с мелкими деталями. Кроме того, современные нейронные сети не могут представлять пространственные и временные производные сигнала, что ограничивает возможности для их применения в физическом моделировании: производные оказывается важным элементом, неявно определенным через уравнения в частных производных, описывающих физические процессы.
Форма представления сигнала, параметризованная с помощью нейронной сети, и обладающая свойствами неявного определения, непрерывности и дифференцируемости, представляет собой отдельное направление в развитии нейронных архитектур. Такой подход способен предложить ряд преимуществ по сравнению с традиционными представлениями и поэтому может быть выделен в отдельную парадигму. Авторы статьи, в рамках новой парадигмы, предлагают использовать функции периодической активации для неявных нейронных представлений. Новый подход, под названием Сети Синусоидального Представления (sinusoidal representation networks) или SIREN, в работе авторов демонстрирует впечатляющие результаты в приложении к сложным сигналам физической природы и их производным.
В основной работе авторы анализируют статистические свойства активации SIREN, чтобы предложить принципиальную новую схему задания начальных значений для весов сети, и демонстрируют работу с изображениями, волновыми полями, видео, звуком и их производными. Далее авторы показывают, как можно использовать SIREN для решения сложных краевых задач, таких, как точное уравнение Эйконала (с получением функций расстояния со знаком), уравнение Пуассона, а также уравнения Гельмгольца и уравнения волнового движения. Наконец, авторы в своей статье объединили SIREN с гиперсетями для изучения априорных вероятностей в пространстве функций SIREN, однако этот материал уже выходит за рамки нашего обзора.
Baselines
Следующие результаты сравнивают SIREN с различными сетевыми архитектурами. TanH, ReLU, Softplus и т. д. означает Multi Layer Perceptron одинакового размера с соответствующей функцией нелинейности. Авторы также сравнивают недавно предложенное позиционное кодирование (Partial Encoding) в сочетании с нелинейной функцией активации ReLU, обозначенной, как ReLU P.E. SIREN существенно превосходит все baseline результаты, сходится значительно быстрее и является единственной архитектурой, точно отражающей градиенты сигнала, позволяя тем самым использование в решении краевых задач.
Представление изображений
SIREN, отображающая координаты 2D-пикселей в цвета, может быть использована для параметризации изображений. В данном случае авторы напрямую активируют SIREN, используя истинные значения пикселей. В данных примерах SIREN удается успешно аппроксимировать изображение, получая на 10 дБ более высокое значение PSNR в условиях меньшего количества итераций по сравнению с конкурентами. Кроме того, SIREN является единственным представителем Multi Layer Perceptron, которому удается точно отразить производные первого и второго порядка.
Краткое демо
(код взят из https://colab.research.google.com/github/vsitzmann/siren/blob/master/explore_siren.ipynb)
Для начала, импортируем библиотеки и добавим вспомогательную функцию для визуализации
import torch
from torch import nn
import torch.nn.functional as F
from torch.utils.data import DataLoader, Dataset
import os
from PIL import Image
from torchvision.transforms import Resize, Compose, ToTensor, Normalize
import numpy as np
import skimage
import matplotlib.pyplot as plt
import time
def get_mgrid(sidelen, dim=2):
'''Generates a flattened grid of (x,y,...) coordinates in a range of -1 to 1.
sidelen: int
dim: int'''
tensors = tuple(dim * [torch.linspace(-1, 1, steps=sidelen)])
mgrid = torch.stack(torch.meshgrid(*tensors), dim=-1)
mgrid = mgrid.reshape(-1, dim)
return mgrid
Теперь добавим реализацию синусоидального слоя, который будет основным строительным блоком SIREN. В данном случае используется гораздо более лаконичная реализация, чем в основном коде авторов, однако упрощение оправдано тем, что здесь не преследуется цель сравнения с baseline решениями.
class SineLayer(nn.Module):
# See paper sec. 3.2, final paragraph, and supplement Sec. 1.5 for discussion of omega_0.
# If is_first=True, omega_0 is a frequency factor which simply multiplies the activations before the
# nonlinearity. Different signals may require different omega_0 in the first layer - this is a
# hyperparameter.
# If is_first=False, then the weights will be divided by omega_0 so as to keep the magnitude of
# activations constant, but boost gradients to the weight matrix (see supplement Sec. 1.5)
def __init__(self, in_features, out_features, bias=True,
is_first=False, omega_0=30):
super().__init__()
self.omega_0 = omega_0
self.is_first = is_first
self.in_features = in_features
self.linear = nn.Linear(in_features, out_features, bias=bias)
self.init_weights()
def init_weights(self):
with torch.no_grad():
if self.is_first:
self.linear.weight.uniform_(-1 / self.in_features,
1 / self.in_features)
else:
self.linear.weight.uniform_(-np.sqrt(6 / self.in_features) / self.omega_0,
np.sqrt(6 / self.in_features) / self.omega_0)
def forward(self, input):
return torch.sin(self.omega_0 * self.linear(input))
def forward_with_intermediate(self, input):
# For visualization of activation distributions
intermediate = self.omega_0 * self.linear(input)
return torch.sin(intermediate), intermediate
class Siren(nn.Module):
def __init__(self, in_features, hidden_features, hidden_layers, out_features, outermost_linear=False,
first_omega_0=30, hidden_omega_0=30.):
super().__init__()
self.net = []
self.net.append(SineLayer(in_features, hidden_features,
is_first=True, omega_0=first_omega_0))
for i in range(hidden_layers):
self.net.append(SineLayer(hidden_features, hidden_features,
is_first=False, omega_0=hidden_omega_0))
if outermost_linear:
final_linear = nn.Linear(hidden_features, out_features)
with torch.no_grad():
final_linear.weight.uniform_(-np.sqrt(6 / hidden_features) / hidden_omega_0,
np.sqrt(6 / hidden_features) / hidden_omega_0)
self.net.append(final_linear)
else:
self.net.append(SineLayer(hidden_features, out_features,
is_first=False, omega_0=hidden_omega_0))
self.net = nn.Sequential(*self.net)
def forward(self, coords):
coords = coords.clone().detach().requires_grad_(True) # allows to take derivative w.r.t. input
output = self.net(coords)
return output, coords
def forward_with_activations(self, coords, retain_grad=False):
'''Returns not only model output, but also intermediate activations.
Only used for visualizing activations later!'''
activations = OrderedDict()
activation_count = 0
x = coords.clone().detach().requires_grad_(True)
activations['input'] = x
for i, layer in enumerate(self.net):
if isinstance(layer, SineLayer):
x, intermed = layer.forward_with_intermediate(x)
if retain_grad:
x.retain_grad()
intermed.retain_grad()
activations['_'.join((str(layer.__class__), "%d" % activation_count))] = intermed
activation_count += 1
else:
x = layer(x)
if retain_grad:
x.retain_grad()
activations['_'.join((str(layer.__class__), "%d" % activation_count))] = x
activation_count += 1
return activations
И, наконец, дифференциальные операторы, которые позволяют использовать
torch.autograd для вычисления градиентов и лапласианов.
def laplace(y, x):
grad = gradient(y, x)
return divergence(grad, x)
def divergence(y, x):
div = 0.
for i in range(y.shape[-1]):
div += torch.autograd.grad(y[..., i], x, torch.ones_like(y[..., i]), create_graph=True)[0][..., i:i+1]
return div
def gradient(y, x, grad_outputs=None):
if grad_outputs is None:
grad_outputs = torch.ones_like(y)
grad = torch.autograd.grad(y, [x], grad_outputs=grad_outputs, create_graph=True)[0]
return grad
Для экспериментов используется классическое изображение оператора.
def get_cameraman_tensor(sidelength):
img = Image.fromarray(skimage.data.camera())
transform = Compose([
Resize(sidelength),
ToTensor(),
Normalize(torch.Tensor([0.5]), torch.Tensor([0.5]))
])
img = transform(img)
return img
Далее просто «фитируем» это изображение. В процессе аппроксимации мы стремимся параметризовать изображение f(x) в оттенках серого с пиксельными координатами x с помощью функции Φ(x). То есть мы ищем функцию Φ такую, что функционал L = ∫Ω∥Φ(x) − f(x)∥dx минимизируется. При этом Ω является областью изображения. Используем небольшой датасет, который вычисляет попиксельные координаты:
class ImageFitting(Dataset):
def __init__(self, sidelength):
super().__init__()
img = get_cameraman_tensor(sidelength)
self.pixels = img.permute(1, 2, 0).view(-1, 1)
self.coords = get_mgrid(sidelength, 2)
def __len__(self):
return 1
def __getitem__(self, idx):
if idx > 0: raise IndexError
return self.coords, self.pixels
Далее создадим экземпляр датасета и SIREN. Поскольку пиксельные координаты являются двумерным вектором, SIREN получает на вход два признака, а поскольку изображение в оттенках серого, размерность выходного канала равна 1.
cameraman = ImageFitting(256)
dataloader = DataLoader(cameraman, batch_size=1, pin_memory=True, num_workers=0)
img_siren = Siren(in_features=2, out_features=1, hidden_features=256,
hidden_layers=3, outermost_linear=True)
img_siren.cuda()
Теперь обучаем нейронную сеть в простом цикле. Всего за несколько сотен итераций хорошо аппроксимируются как изображение, так и его градиенты.
total_steps = 500 # Since the whole image is our dataset, this just means 500 gradient descent steps.
steps_til_summary = 10
optim = torch.optim.Adam(lr=1e-4, params=img_siren.parameters())
model_input, ground_truth = next(iter(dataloader))
model_input, ground_truth = model_input.cuda(), ground_truth.cuda()
for step in range(total_steps):
model_output, coords = img_siren(model_input)
loss = ((model_output - ground_truth)**2).mean()
if not step % steps_til_summary:
print("Step %d, Total loss %0.6f" % (step, loss))
img_grad = gradient(model_output, coords)
img_laplacian = laplace(model_output, coords)
fig, axes = plt.subplots(1,3, figsize=(18,6))
axes[0].imshow(model_output.cpu().view(256,256).detach().numpy())
axes[1].imshow(img_grad.norm(dim=-1).cpu().view(256,256).detach().numpy())
axes[2].imshow(img_laplacian.cpu().view(256,256).detach().numpy())
plt.show()
optim.zero_grad()
loss.backward()
optim.step()
Представление аудио
Начнем с небольшого эксперимента.
Будем использовать SIREN для параметризации аудиосигнала, то есть стремимся параметризовать звуковую волну f(t) в моменты времени t с помощью функции Φ. Для этого ищем функцию Φ такую, что: функция потерь L = ∫Ω∥Φ(t) −f(t)∥dt минимизируется, где Ω является звуковой волной. Для эксперимента будем использовать сонату Баха:
import scipy.io.wavfile as wavfile
import io
from IPython.display import Audio
if not os.path.exists('gt_bach.wav'):
!wget https://vsitzmann.github.io/siren/img/audio/gt_bach.wav
Создадим небольшой датасет, который позволяет перевести аудиофайл в более удобный для работы формат:
class AudioFile(torch.utils.data.Dataset):
def __init__(self, filename):
self.rate, self.data = wavfile.read(filename)
self.data = self.data.astype(np.float32)
self.timepoints = get_mgrid(len(self.data), 1)
def get_num_samples(self):
return self.timepoints.shape[0]
def __len__(self):
return 1
def __getitem__(self, idx):
amplitude = self.data
scale = np.max(np.abs(amplitude))
amplitude = (amplitude / scale)
amplitude = torch.Tensor(amplitude).view(-1, 1)
return self.timepoints, amplitude
Далее создадим экземпляр SIREN. Поскольку звуковой сигнал имеет гораздо более высокую пространственную частоту в диапазоне от -1 до 1, поэтому увеличиваем ω0 в первом слое SIREN.
bach_audio = AudioFile('gt_bach.wav')
dataloader = DataLoader(bach_audio, shuffle=True, batch_size=1, pin_memory=True, num_workers=0)
# Note that we increase the frequency of the first layer to match the higher frequencies of the
# audio signal. Equivalently, we could also increase the range of the input coordinates.
audio_siren = Siren(in_features=1, out_features=1, hidden_features=256,
hidden_layers=3, first_omega_0=3000, outermost_linear=True)
audio_siren.cuda()
Давайте прослушаем исходные данные:
rate, _ = wavfile.read('gt_bach.wav')
model_input, ground_truth = next(iter(dataloader))
Audio(ground_truth.squeeze().numpy(),rate=rate)
Далее начнем обучение нейронной сети:
total_steps = 1000
steps_til_summary = 100
optim = torch.optim.Adam(lr=1e-4, params=audio_siren.parameters())
model_input, ground_truth = next(iter(dataloader))
model_input, ground_truth = model_input.cuda(), ground_truth.cuda()
for step in range(total_steps):
model_output, coords = audio_siren(model_input)
loss = F.mse_loss(model_output, ground_truth)
if not step % steps_til_summary:
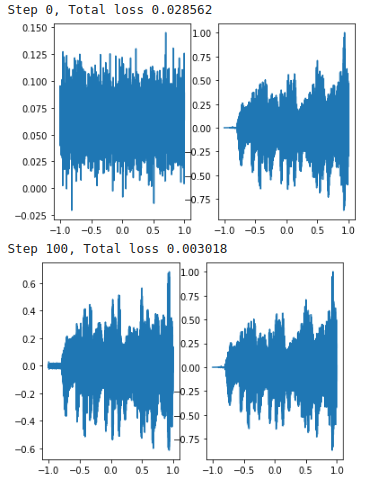
print("Step %d, Total loss %0.6f" % (step, loss))
fig, axes = plt.subplots(1,2)
axes[0].plot(coords.squeeze().detach().cpu().numpy(),model_output.squeeze().detach().cpu().numpy())
axes[1].plot(coords.squeeze().detach().cpu().numpy(),ground_truth.squeeze().detach().cpu().numpy())
plt.show()
optim.zero_grad()
loss.backward()
optim.step()
Послушаем, что получается в итоге:
final_model_output, coords = audio_siren(model_input)
Audio(final_model_output.cpu().detach().squeeze().numpy(),rate=rate)
SIREN с одиночным входом, соответствующим координате времени, и скалярным выходом действительно может успешно параметризировать аудиосигналы. SIREN — единственная сетевая архитектура, которая успешно воспроизводит аудиосигнал как для музыки, так и для человеческого голоса.

Представление видео
Использование SIREN совместно на координатах пикселей и времени позволяет параметризовать видео. В данном случае SIREN непосредственно активируется на истинных значениях пикселей и позволяет параметризовать видео существенно лучше, чем ReLU Multi Layer Perceptron.
Решение уравнения Пуассона
Используя только производные в подходе SIREN, возможно решить уравнение Пуассона. SIREN — это опять-таки единственная архитектура, которая аппроксимирует изображения, градиенты и области лапласиан точно и быстро.
Представление фигур путем решения уравнения Эйконала Interactive 3D SDF Viewer — используйте мышь для навигации по сценам
Решая краевую задачу в форме уравнений Эйконала, мы можем восстановить SDF из облака точек и нормалей поверхности. Подход SIREN позволяет восстановить сцену масштаба комнаты на основе только облака точек и нормалей поверхности, при этом удается точно воспроизвести мелкие детали, а для обучения требуется менее одного часа. В отличие от недавних работ по объединению воксельных сеток с нейронными неявными представлениями, в предлагаемом подходе полное представление хранится в весах одной пятислойной нейронной сети, без 2D или 3D-сверток, и поэтому требует гораздо меньшего количества параметров. Важно обратить внимание на то, что полученные SDF не обучаются на исходных значениях SDF, а скорее являются результатом решения вышеупомянутой эйкональной краевой задачи. Такая постановка задачи является существенно более сложной и требует обучения с учителем по градиентам (детали — в статье). В результате архитектуры сетей, градиенты которых хуже контролируются, показывают качество ниже, чем в подходе SIREN.
Решение уравнения Гельмгольца
В данном случае авторы используют подход SIREN для решения неоднородного уравнения Гельмгольца. Архитектуры на основе ReLU и Tanh не позволяют полностью решить эту задачу.
Решение волнового уравнения
При работе со временем, подход SIREN позволяет успешно решить волновое уравнение, в отличие от архитектуры на основе Tanh, которая не смогла сойтись к правильному решению.
* * *
Предлагаемое авторами представление SIREN для глубокого обучения помогает в работе с такими данными, как изображения, аудио- и видеосигналы. Новый подход может быть полезным в таких областях, как классификация изображений или speech-to-text в рамках работы со звуком. За счет больших возможностей SIREN по точному воспроизведению сигнала, а также градиентов и лапласианов можно ожидать, что генеративные модели с использованием SIREN смогут совершить качественный скачок в своих возможностях.
В данный момент мы рассматриваем возможности проверить SIREN на наших задачах в Центре компетенции больших данных и искусственного интеллекта ЛАНИТ. Хочется надеяться, что предлагаемый подход покажет свою продуктивность не только на простых примерах, но и на нетривиальных прикладных задачах.