В Учи.ру мы стараемся даже небольшие улучшения выкатывать A/B-тестом, только за этот учебный год их было больше 250. A/B-тест — мощнейший инструмент тестирования изменений, без которого сложно представить нормальное развитие интернет-продукта. В то же время, несмотря на кажущуюся простоту, при проведении A/B-теста можно допустить серьёзные ошибки как на этапе дизайна эксперимента, так и при подведении итогов. В этой статье я расскажу о некоторых технических моментах проведения теста: как мы определяем срок тестирования, подводим итоги и как избегаем ошибочных результатов при досрочном завершении тестов и при тестировании сразу нескольких гипотез.

Типичная схема A/B-тестирования у нас (да и у многих) выглядит так:
Всё выглядит логично и просто, дьявол, как всегда, в деталях.
В любом A/B-тесте присутствует элемент случайности: метрики групп зависят не только от их функционала, но и от того, какие пользователи в них попали и как они себя ведут. Чтобы достоверно сделать выводы о превосходстве какой-то группы, нужно набрать достаточно наблюдений в тесте, но даже тогда вы не застрахованы от ошибок. Их различают два типа:
При большом количестве экспериментов важно, чтобы вероятность ошибки первого рода была мала. Её можно контролировать с помощью статистических методов. Например, мы хотим, чтобы в каждом эксперименте вероятность ошибки первого рода не превышала 5% (это просто удобное значение, для собственных нужд можно брать другое). Тогда мы будем принимать эксперименты на уровне значимости 0.05:
Проверить гипотезу можно параметрическим или непараметрическим критерием. Параметрические опираются на параметры выборочного распределения случайной величины и обладают большей мощностью (реже допускают ошибки второго рода), но предъявляют требования к распределению исследуемой случайной величины.
Самый распространенный параметрический тест — критерий Стьюдента. Для двух независимых выборок (случай A/B-теста) его иногда называют критерием Уэлча. Этот критерий работает корректно, если исследуемые величины распределены нормально. Может показаться, что на реальных данных это требование почти никогда не удовлетворяется, однако на самом деле тест требует нормального распределения выборочных средних, а не самих выборок. На практике это означает, что критерий можно применять, если у вас в тесте достаточно много наблюдений (десятки-сотни) и в распределениях нет совсем уж длинных хвостов. При этом характер распределения исходных наблюдений неважен. Читатель самостоятельно может убедиться, что критерий Стьюдента работает корректно даже на выборках, сгенерированных из распределений Бернулли или экспоненциального.
Из непараметрических критериев популярен критерий Манна — Уитни. Его стоит применять, если ваши выборки очень малого размера или есть большие выбросы (метод сравнивает медианы, поэтому устойчив к выбросам). Также для корректной работы критерия в выборках должно быть мало совпадающих значений. На практике нам ни разу не приходилось применять непараметрические критерии, в своих тестах всегда пользуемся критерием Стьюдента.
Самая очевидная и простая проблема: если в тесте кроме контрольной группы есть несколько экспериментальных, то подведение итогов с уровнем значимости 0.05 приведёт к кратному росту доли ошибок первого рода. Так происходит, потому что при каждом применении статистического критерия вероятность ошибки первого рода будет 5%. При количестве групп и уровне значимости
и уровне значимости  вероятность, что какая-то экспериментальная группа выиграет случайно, составляет:
вероятность, что какая-то экспериментальная группа выиграет случайно, составляет:
Например, для трёх экспериментальных групп получим 14.3% вместо ожидаемых 5%. Решается проблема поправкой Бонферрони на множественную проверку гипотез: нужно просто поделить уровень значимости на количество сравнений (то есть групп) и работать с ним. Для примера выше уровень значимости с учётом поправки составит 0.05/3 = 0.0167 и вероятность хотя бы одной ошибки первого рода составит приемлемые 4.9%.
Строго говоря, сравнения групп по разным метрикам или срезам аудитории тоже подвержены проблеме множественного тестирования. Формально учесть все проверки довольно сложно, потому что их количество сложно спрогнозировать заранее и подчас они не являются независимыми (особенно если речь идёт про разные метрики, а не срезы). Универсального рецепта нет, полагайтесь на здравый смысл и помните, что если проверить достаточно много срезов по разным метрикам, то в любом тесте можно увидеть якобы статистически значимый результат. А значит, надо с осторожностью относиться, например, к значимому приросту ретеншена пятого дня новых мобильных пользователей из крупных городов.
Частный случай множественного тестирования гипотез — проблема подглядывания (peeking problem). Смысл в том, что значение p-value по ходу теста может случайно опускаться ниже принятого уровня значимости. Если внимательно следить за экспериментом, то можно поймать такой момент и ошибочно сделать вывод о статистической значимости.
Предположим, что мы отошли от описанной в начале поста схемы проведения тестов и решили подводить итоги на уровне значимости 5% каждый день (или просто больше одного раза за время теста). Под подведением итогов я понимаю признание теста положительным, если p-value ниже 0.05, и его продолжение в противном случае. При такой стратегии доля ложноположительных результатов будет пропорциональна количеству проверок и уже за первый месяц достигнет 28%. Такая огромная разница кажется контринтуитивной, поэтому обратимся к методике A/A-тестов, незаменимой для разработки схем A/B-тестирования.
Идея A/A-теста проста: симулировать на исторических данных много A/B-тестов со случайным разбиением на группы. Разницы между группами заведомо нет, поэтому можно точно оценить долю ошибок первого рода в своей схеме A/B-тестирования. На гифке ниже показано, как изменяются значения p-value по дням для четырёх таких тестов. Равный 0.05 уровень значимости обозначен пунктирной линией. Когда p-value опускается ниже, мы окрашиваем график теста в красный. Если бы в этом время подводились итоги теста, он был бы признан успешным.
Рассчитаем аналогично 10 тысяч A/A-тестов продолжительностью в один месяц и сравним доли ложноположительных результатов в схеме с подведением итогов в конце срока и каждый день. Для наглядности приведём графики блуждания p-value по дням для первых 100 симуляций. Каждая линия — p-value одного теста, красным выделены траектории тестов, в итоге ошибочно признанных удачными (чем меньше, тем лучше), пунктирная линия — требуемое значение p-value для признания теста успешным.
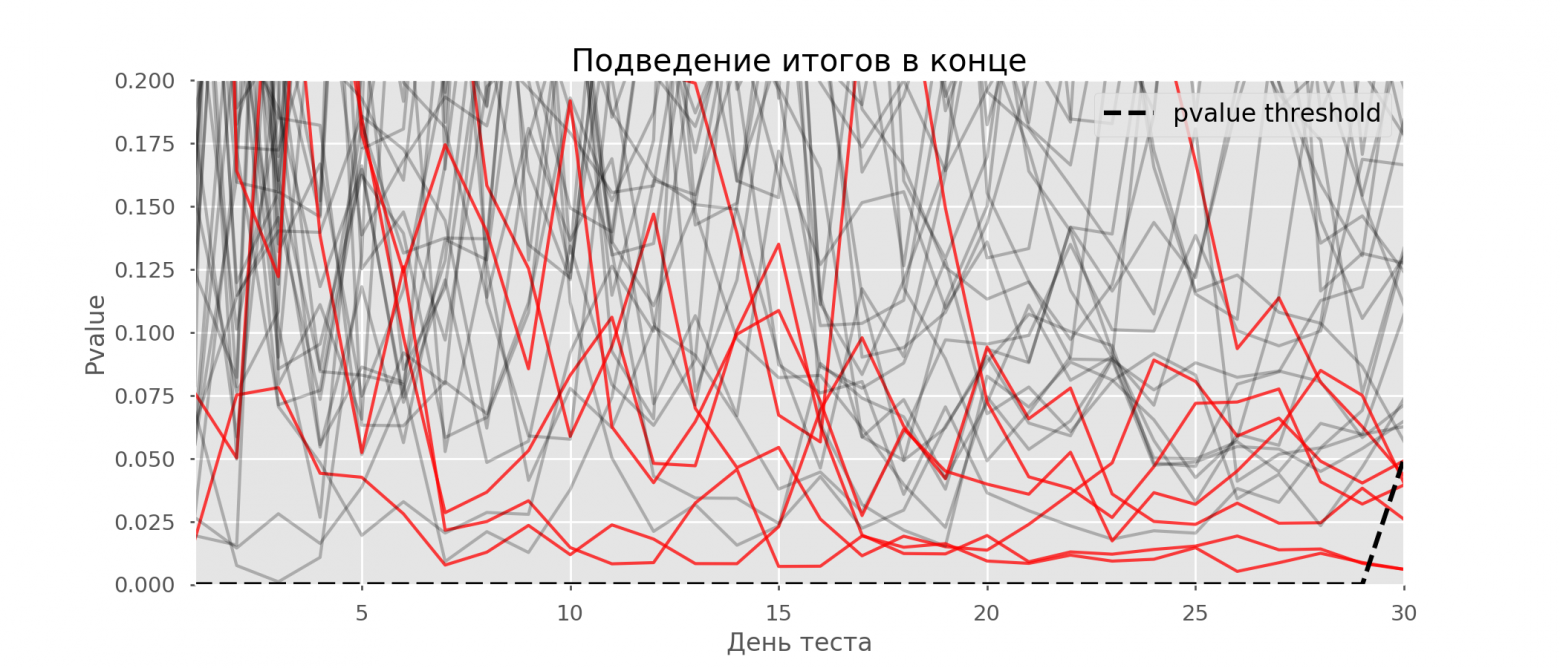
На графике можно насчитать 7 ложноположительных тестов, а всего среди 10 тысяч их было 502, или 5%. Хочется отметить, что p-value многих тестов по ходу наблюдений опускались ниже 0.05, но к концу наблюдений выходили за пределы уровня значимости. Теперь оценим схему тестирования с подведением итогов каждый день:
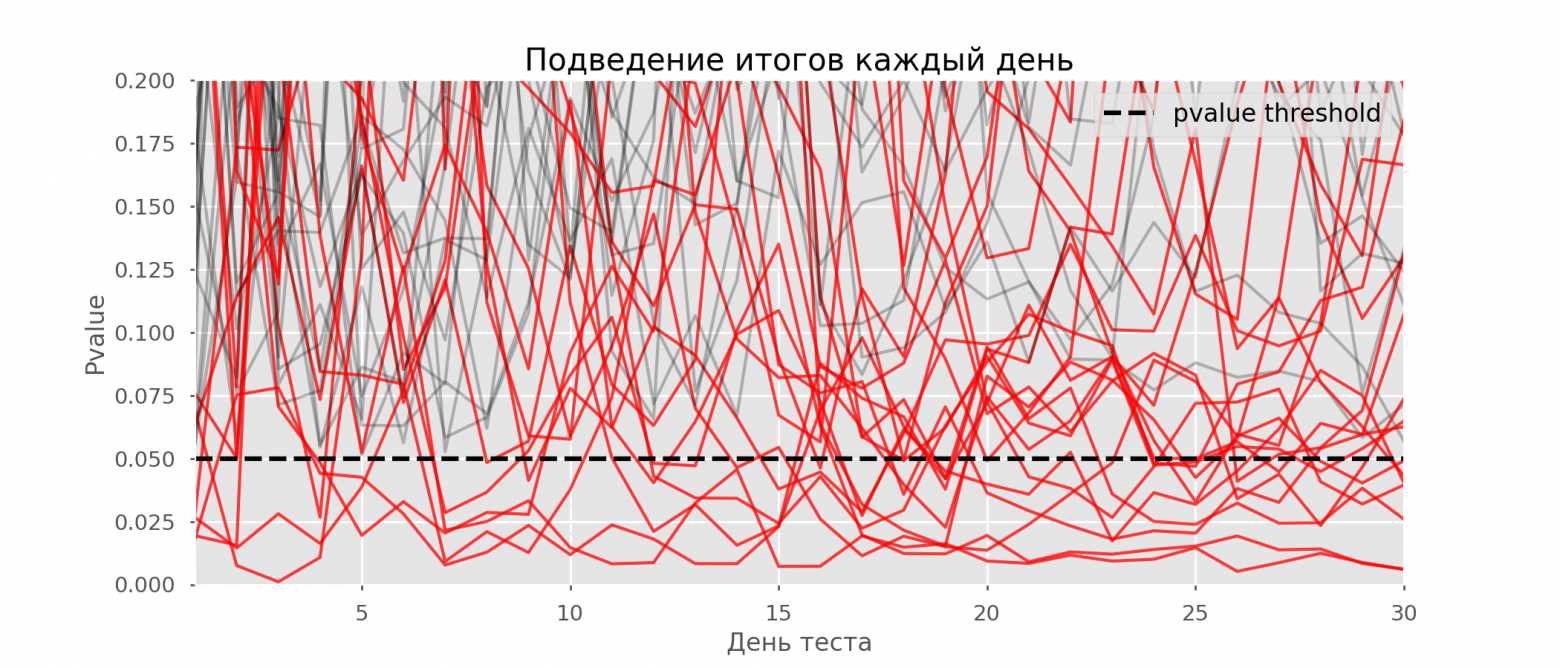
Красных линий настолько много, что уже ничего не понятно. Перерисуем, обрывая линии тестов, как только их p-value достигнут критического значения:

Всего будет 2813 ложноположительных тестов из 10 тысяч, или 28%. Понятно, что такая схема нежизнеспособна.
Хоть проблема подглядывания — это частный случай множественного тестирования, применять стандартные поправки (Бонферрони и другие) здесь не стоит, потому что они окажутся излишне консервативными. На графике ниже — доля ложноположительных результатов в зависимости от количества тестируемых групп (красная линия) и количества подглядываний (зелёная линия).
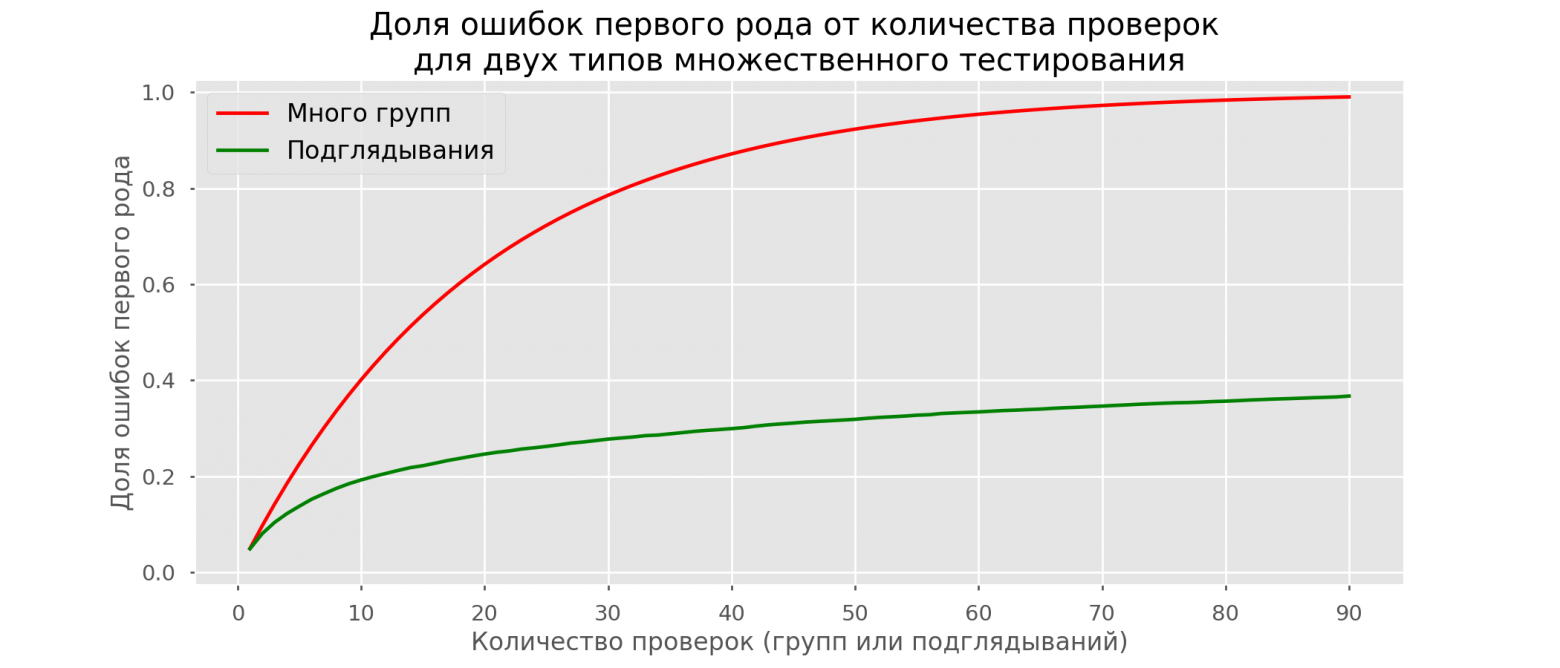
Хотя на бесконечности и в подглядываниях мы вплотную приблизимся к 1, доля ошибок растёт гораздо медленнее. Это объясняется тем, что сравнения в этом случае независимыми уже не являются.
Есть варианты тестирования, позволяющие досрочно принять тест. Расскажу о двух из них: с постоянным уровнем значимости (поправка Pocock’a) и зависимым от номера подглядывания (поправка O'Brien-Fleming’a). Строго говоря, для обеих поправок нужно заранее знать максимальный срок теста и количество проверок между запуском и окончанием теста. Причём проверки должны происходить примерно через равные промежутки времени (или через равные количества наблюдений).
Метод заключается в том, что мы подводим итоги тестов каждый день, но при сниженном (более строгом) уровне значимости. Например, если мы знаем, что сделаем не больше 30 проверок, то уровень значимости надо выставить равным 0.006 (подбирается в зависимости от количества подглядываний методом Монте-Карло, то есть эмпирически). На нашей симуляции получим 4% ложноположительных исходов — видимо, порог можно было увеличить.

Несмотря на кажущуюся наивность, некоторые крупные компании пользуются именно этим способом. Он очень прост и надёжен, если вы принимаете решения по чувствительным метрикам и на большом трафике. Например, в «Авито» по умолчанию уровень значимости принят за 0.005.
В этом методе уровень значимости изменяется в зависимости от номера проверки. Надо заранее определить количество шагов (или подглядываний) в тесте и рассчитать уровень значимости для каждого из них. Чем раньше мы пытаемся завершить тест, тем более жёсткий критерий будет применён. Пороговые значения статистики Стьюдента (в том числе значение на последнем шаге
(в том числе значение на последнем шаге  ), соответствующие нужному уровню значимости, зависят от номера проверки
), соответствующие нужному уровню значимости, зависят от номера проверки  (принимает значения от 1 до общего количества проверок
(принимает значения от 1 до общего количества проверок  включительно) и рассчитываются по эмпирически полученной формуле:
включительно) и рассчитываются по эмпирически полученной формуле:
Соответствующие уровни значимости вычисляются через перцентиль стандартного распределения, соответствующий значению статистики Стьюдента
стандартного распределения, соответствующий значению статистики Стьюдента  :
:
На тех же симуляциях это выглядит так:

Ложноположительных результатов получилось 501 из 10 тысяч, или ожидаемые 5%. Обратите внимание, что уровень значимости не достигает значения в 5% даже в конце, так как эти 5% должны «размазаться» по всем проверкам. В компании мы пользуемся именно этой поправкой, если запускаем тест с возможностью ранней остановки. Прочитать про эти же и другие поправки можно по ссылке.
Специфика нашего продукта такова, что распределение любой метрики очень сильно меняется в зависимости от аудитории теста (например, номера класса) и времени года. Поэтому не получится принять за дату окончания теста правила в духе «тест закончится, когда в каждой группе наберётся 1 млн пользователей» или «тест закончится, когда количество решённых заданий достигнет 100 млн». То есть получится, но на практике для этого надо будет учесть слишком много факторов:
Тем не менее, в наших схемах A/B-тестирования всегда нужно заранее фиксировать дату окончания. Для прогноза продолжительности теста мы разработали внутреннее приложение — калькулятор A/B-тестов. Основываясь на активности пользователей из выбранного сегмента за прошлый год, приложение рассчитывает срок, на который надо запустить тест, чтобы значимо зафиксировать аплифт в X% по выбранной метрике. Также автоматически учитывается поправка на множественную проверку и рассчитываются пороговые уровни значимости для досрочной остановки теста.

Все метрики у нас рассчитываются на уровне объектов теста. Если метрика — количество решённых задач, то в тесте на уровне учителей это будет сумма решённых задач его учениками. Так как мы пользуемся критерием Стьюдента, можно заранее рассчитать нужные калькулятору агрегаты по всем возможным срезам. Для каждого дня со старта теста нужно знать количество людей в тесте , среднее значение метрики
, среднее значение метрики  и её дисперсию
и её дисперсию  . Зафиксировав доли контрольной группы
. Зафиксировав доли контрольной группы  , экспериментальной группы
, экспериментальной группы  и ожидаемый прирост от теста
и ожидаемый прирост от теста  в процентах, можно рассчитать ожидаемые значения статистики Стьюдента
в процентах, можно рассчитать ожидаемые значения статистики Стьюдента  и соответствующее p-value на каждый день теста:
и соответствующее p-value на каждый день теста:
Далее легко получить значения p-value на каждый день:
Зная p-value и уровень значимости с учетом всех поправок на каждый день теста, для любой продолжительности теста можно рассчитать минимальный аплифт, который можно задетектировать (в англоязычной литературе — MDE, minimal detectable effect). После этого легко решить обратную задачу — определить количество дней, необходимое для выявления ожидаемого аплифта.
В качестве заключения хочу напомнить основные посылы статьи:
Несмотря на всё вышенаписанное, бизнес и здравый смысл не должны страдать в угоду математической строгости. Иногда можно выкатить на всех функционал, не показавший значимого прироста в тесте, какие-то изменения неизбежно происходят вообще без тестирования. Но если вы проводите сотни тестов в год, их аккуратный анализ особенно важен. Иначе есть риск, что количество ложноположительных тестов будет сравнимо с реально полезными.

Типичная схема A/B-тестирования у нас (да и у многих) выглядит так:
- Разрабатываем фичу, но перед раскаткой на всю аудиторию хотим убедиться, что она улучшает целевую метрику, например, вовлечённость.
- Определяем срок, на который запускается тест.
- Случайно разбиваем пользователей на две группы.
- Одной группе показываем версию продукта с фичей (экспериментальная группа), другой — старую (контрольная).
- В процессе мониторим метрику, чтобы вовремя прекратить особо неудачный тест.
- По истечении срока теста сравниваем метрику в экспериментальной и контрольной группах.
- Если метрика в экспериментальной группе статистически значимо лучше, чем в контрольной, раскатываем протестированную фичу на всех. Если же статистической значимости нет, завершаем тест с отрицательным результатом.
Всё выглядит логично и просто, дьявол, как всегда, в деталях.
Статистическая значимость, критерии и ошибки
В любом A/B-тесте присутствует элемент случайности: метрики групп зависят не только от их функционала, но и от того, какие пользователи в них попали и как они себя ведут. Чтобы достоверно сделать выводы о превосходстве какой-то группы, нужно набрать достаточно наблюдений в тесте, но даже тогда вы не застрахованы от ошибок. Их различают два типа:
- Ошибка первого рода происходит, если мы фиксируем разницу между группами, хотя на самом деле её нет. В тексте также будет встречаться эквивалентный термин — ложноположительный результат. Статья посвящена именно таким ошибкам.
- Ошибка второго рода происходит, если мы фиксируем отсутствие разницы, хотя на самом деле она есть.
При большом количестве экспериментов важно, чтобы вероятность ошибки первого рода была мала. Её можно контролировать с помощью статистических методов. Например, мы хотим, чтобы в каждом эксперименте вероятность ошибки первого рода не превышала 5% (это просто удобное значение, для собственных нужд можно брать другое). Тогда мы будем принимать эксперименты на уровне значимости 0.05:
- Есть A/B-тест с контрольной группой A и экспериментальной — B. Цель — проверить, что группа B отличается от группы A по какой-то метрике.
- Формулируем нулевую статистическую гипотезу: группы A и B не отличаются, а наблюдаемые различия объясняются шумом. По умолчанию всегда считаем, что разницы нет, пока не доказано обратное.
- Проверяем гипотезу строгим математическим правилом — статистическим критерием, например, критерием Стьюдента.
- В результате получаем величину p-value. Она лежит в диапазоне от 0 до 1 и означает вероятность увидеть текущую или более экстремальную разницу между группами при условии верности нулевой гипотезы, то есть при отсутствии разницы между группами.
- Значение p-value сравнивается с уровнем значимости 0.05. Если оно больше, принимаем нулевую гипотезу о том, что различий нет, иначе считаем, что между группами есть статистически значимая разница.
Проверить гипотезу можно параметрическим или непараметрическим критерием. Параметрические опираются на параметры выборочного распределения случайной величины и обладают большей мощностью (реже допускают ошибки второго рода), но предъявляют требования к распределению исследуемой случайной величины.
Самый распространенный параметрический тест — критерий Стьюдента. Для двух независимых выборок (случай A/B-теста) его иногда называют критерием Уэлча. Этот критерий работает корректно, если исследуемые величины распределены нормально. Может показаться, что на реальных данных это требование почти никогда не удовлетворяется, однако на самом деле тест требует нормального распределения выборочных средних, а не самих выборок. На практике это означает, что критерий можно применять, если у вас в тесте достаточно много наблюдений (десятки-сотни) и в распределениях нет совсем уж длинных хвостов. При этом характер распределения исходных наблюдений неважен. Читатель самостоятельно может убедиться, что критерий Стьюдента работает корректно даже на выборках, сгенерированных из распределений Бернулли или экспоненциального.
Из непараметрических критериев популярен критерий Манна — Уитни. Его стоит применять, если ваши выборки очень малого размера или есть большие выбросы (метод сравнивает медианы, поэтому устойчив к выбросам). Также для корректной работы критерия в выборках должно быть мало совпадающих значений. На практике нам ни разу не приходилось применять непараметрические критерии, в своих тестах всегда пользуемся критерием Стьюдента.
Проблема множественного тестирования гипотез
Самая очевидная и простая проблема: если в тесте кроме контрольной группы есть несколько экспериментальных, то подведение итогов с уровнем значимости 0.05 приведёт к кратному росту доли ошибок первого рода. Так происходит, потому что при каждом применении статистического критерия вероятность ошибки первого рода будет 5%. При количестве групп
Например, для трёх экспериментальных групп получим 14.3% вместо ожидаемых 5%. Решается проблема поправкой Бонферрони на множественную проверку гипотез: нужно просто поделить уровень значимости на количество сравнений (то есть групп) и работать с ним. Для примера выше уровень значимости с учётом поправки составит 0.05/3 = 0.0167 и вероятность хотя бы одной ошибки первого рода составит приемлемые 4.9%.
Метод Холма — Бонферрони
Искушенный читатель знает и о методе Холма — Бонферрони, который всегда обладает большей мощностью, чем поправка Бонферрони, то есть реже совершает ошибки второго рода. В этом методе мы сортируем  гипотез по возрастанию значений p-value и начинаем их сравнивать по порядку с требуемым уровнем значимости, который увеличивается в зависимости от номера шага
гипотез по возрастанию значений p-value и начинаем их сравнивать по порядку с требуемым уровнем значимости, который увеличивается в зависимости от номера шага  по формуле:
по формуле:
P-value первой гипотезы сравнивается с уровнем статистический значимости . Если гипотеза принимается, то переходим ко второй и сравниваем её p-value с уровнем статистической значимости
. Если гипотеза принимается, то переходим ко второй и сравниваем её p-value с уровнем статистической значимости  , и так далее. Как только какая-то гипотеза отвергается, процесс останавливается и все оставшиеся гипотезы так же отвергаются. Самое жёсткое требование (и такое же, как в поправке Бонферрони) накладывается на гипотезу с наименьшим p-value, а большая мощность достигается за счёт менее жёстких условий для последующих гипотез. Цель A/B-теста — выбрать одного единственного победителя, поэтому методы Бонферрони и Холма — Бонферрони абсолютно идентичны в этом приложении.
, и так далее. Как только какая-то гипотеза отвергается, процесс останавливается и все оставшиеся гипотезы так же отвергаются. Самое жёсткое требование (и такое же, как в поправке Бонферрони) накладывается на гипотезу с наименьшим p-value, а большая мощность достигается за счёт менее жёстких условий для последующих гипотез. Цель A/B-теста — выбрать одного единственного победителя, поэтому методы Бонферрони и Холма — Бонферрони абсолютно идентичны в этом приложении.
P-value первой гипотезы сравнивается с уровнем статистический значимости
Строго говоря, сравнения групп по разным метрикам или срезам аудитории тоже подвержены проблеме множественного тестирования. Формально учесть все проверки довольно сложно, потому что их количество сложно спрогнозировать заранее и подчас они не являются независимыми (особенно если речь идёт про разные метрики, а не срезы). Универсального рецепта нет, полагайтесь на здравый смысл и помните, что если проверить достаточно много срезов по разным метрикам, то в любом тесте можно увидеть якобы статистически значимый результат. А значит, надо с осторожностью относиться, например, к значимому приросту ретеншена пятого дня новых мобильных пользователей из крупных городов.
Проблема подглядывания
Частный случай множественного тестирования гипотез — проблема подглядывания (peeking problem). Смысл в том, что значение p-value по ходу теста может случайно опускаться ниже принятого уровня значимости. Если внимательно следить за экспериментом, то можно поймать такой момент и ошибочно сделать вывод о статистической значимости.
Предположим, что мы отошли от описанной в начале поста схемы проведения тестов и решили подводить итоги на уровне значимости 5% каждый день (или просто больше одного раза за время теста). Под подведением итогов я понимаю признание теста положительным, если p-value ниже 0.05, и его продолжение в противном случае. При такой стратегии доля ложноположительных результатов будет пропорциональна количеству проверок и уже за первый месяц достигнет 28%. Такая огромная разница кажется контринтуитивной, поэтому обратимся к методике A/A-тестов, незаменимой для разработки схем A/B-тестирования.
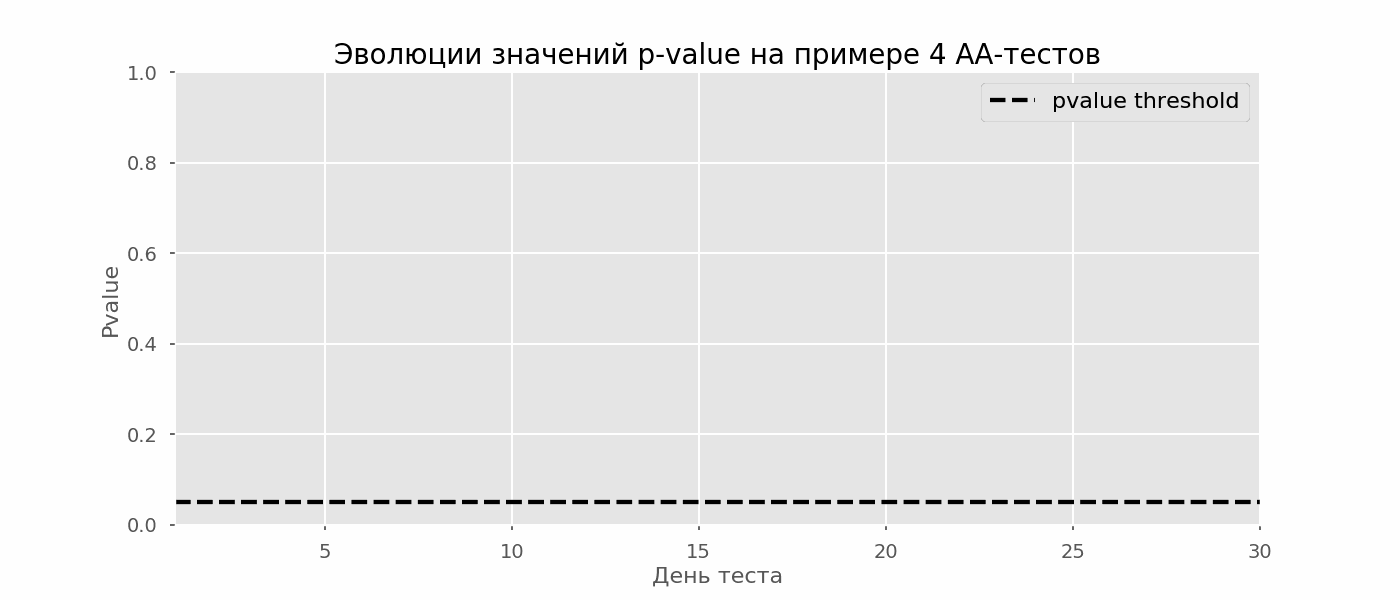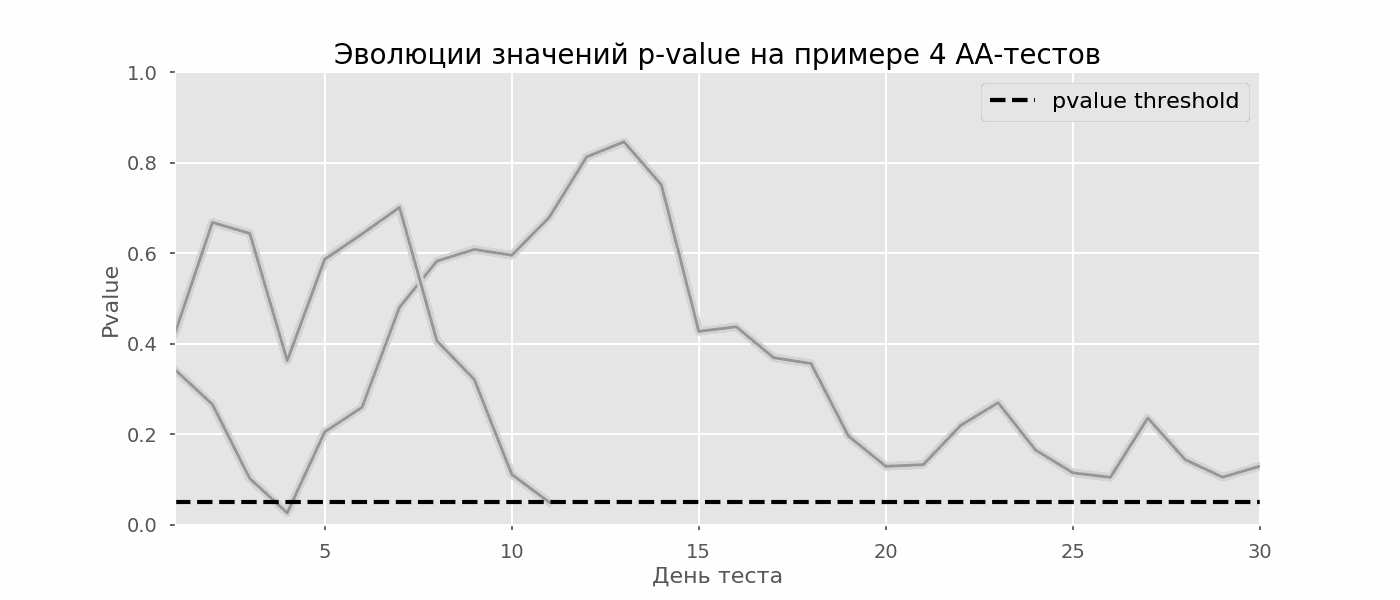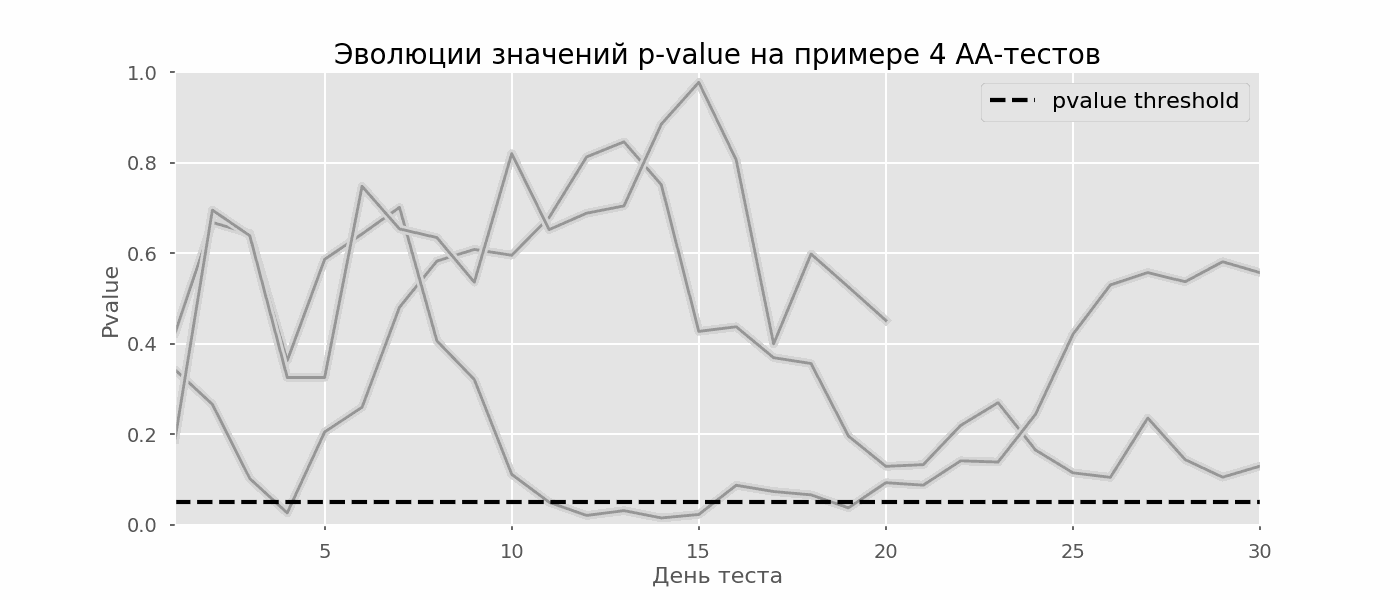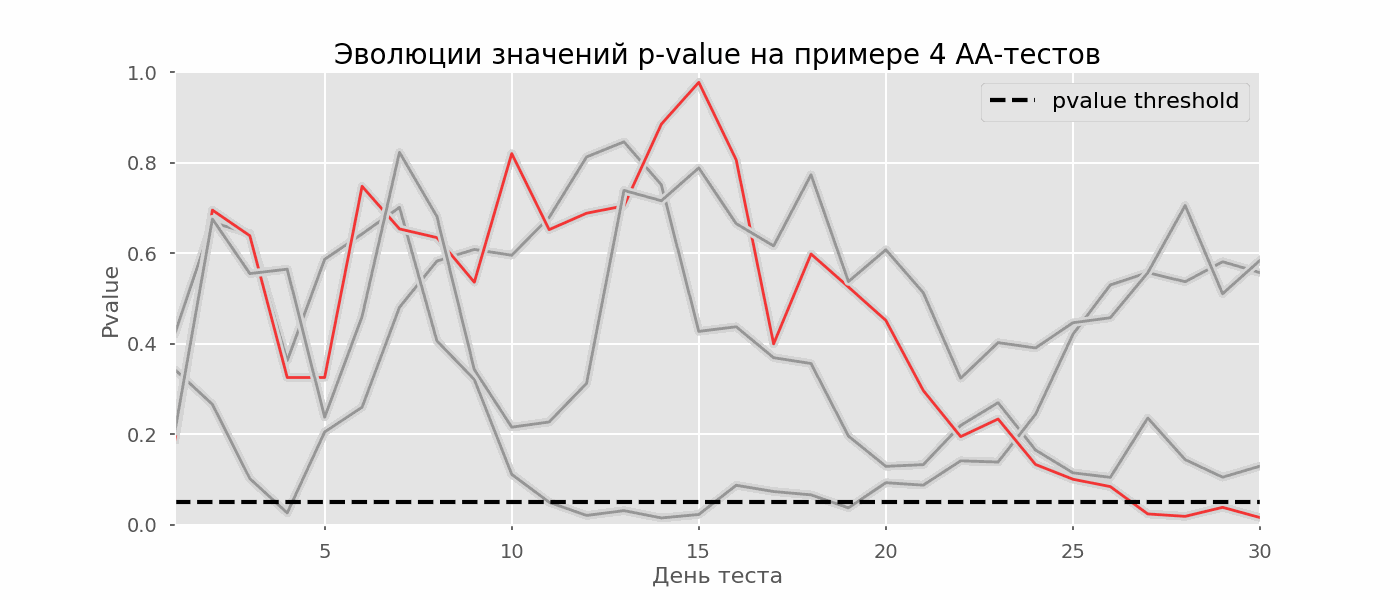
Идея A/A-теста проста: симулировать на исторических данных много A/B-тестов со случайным разбиением на группы. Разницы между группами заведомо нет, поэтому можно точно оценить долю ошибок первого рода в своей схеме A/B-тестирования. На гифке ниже показано, как изменяются значения p-value по дням для четырёх таких тестов. Равный 0.05 уровень значимости обозначен пунктирной линией. Когда p-value опускается ниже, мы окрашиваем график теста в красный. Если бы в этом время подводились итоги теста, он был бы признан успешным.

Рассчитаем аналогично 10 тысяч A/A-тестов продолжительностью в один месяц и сравним доли ложноположительных результатов в схеме с подведением итогов в конце срока и каждый день. Для наглядности приведём графики блуждания p-value по дням для первых 100 симуляций. Каждая линия — p-value одного теста, красным выделены траектории тестов, в итоге ошибочно признанных удачными (чем меньше, тем лучше), пунктирная линия — требуемое значение p-value для признания теста успешным.
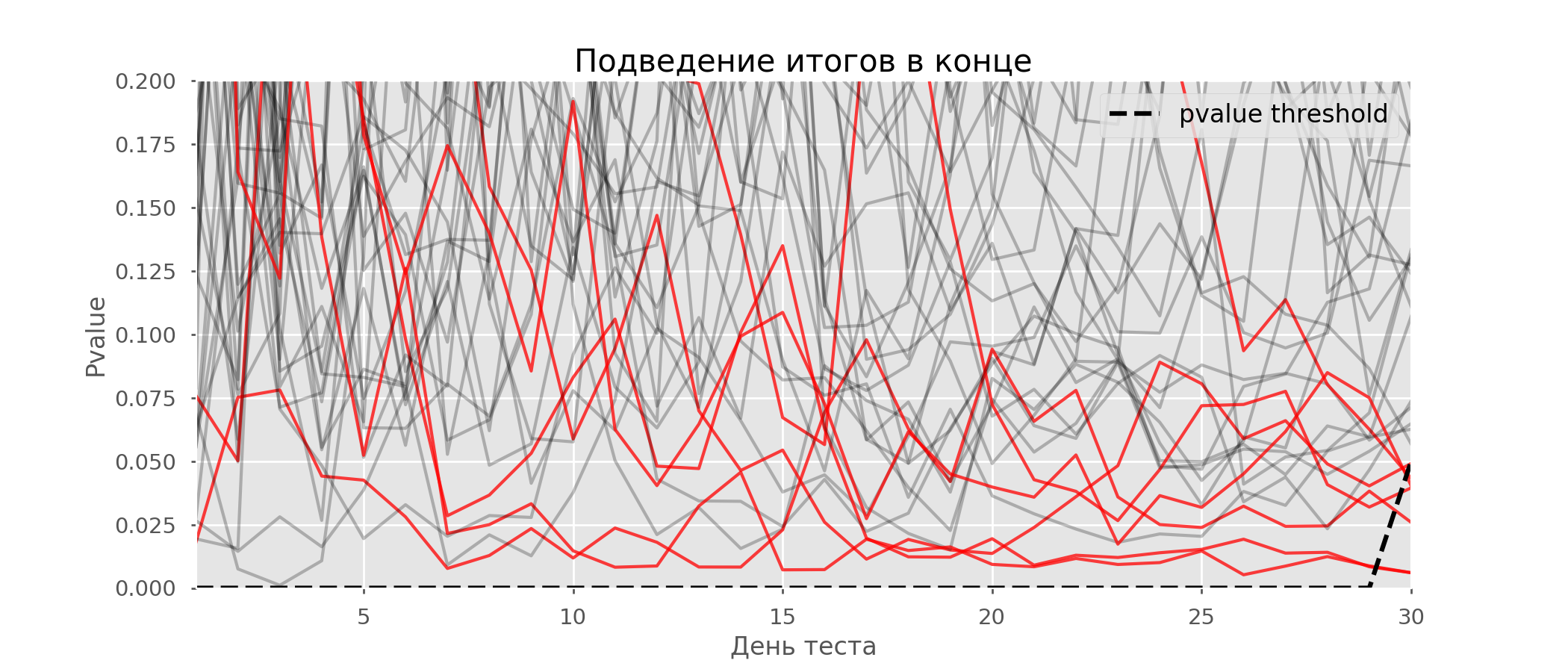
На графике можно насчитать 7 ложноположительных тестов, а всего среди 10 тысяч их было 502, или 5%. Хочется отметить, что p-value многих тестов по ходу наблюдений опускались ниже 0.05, но к концу наблюдений выходили за пределы уровня значимости. Теперь оценим схему тестирования с подведением итогов каждый день:

Красных линий настолько много, что уже ничего не понятно. Перерисуем, обрывая линии тестов, как только их p-value достигнут критического значения:
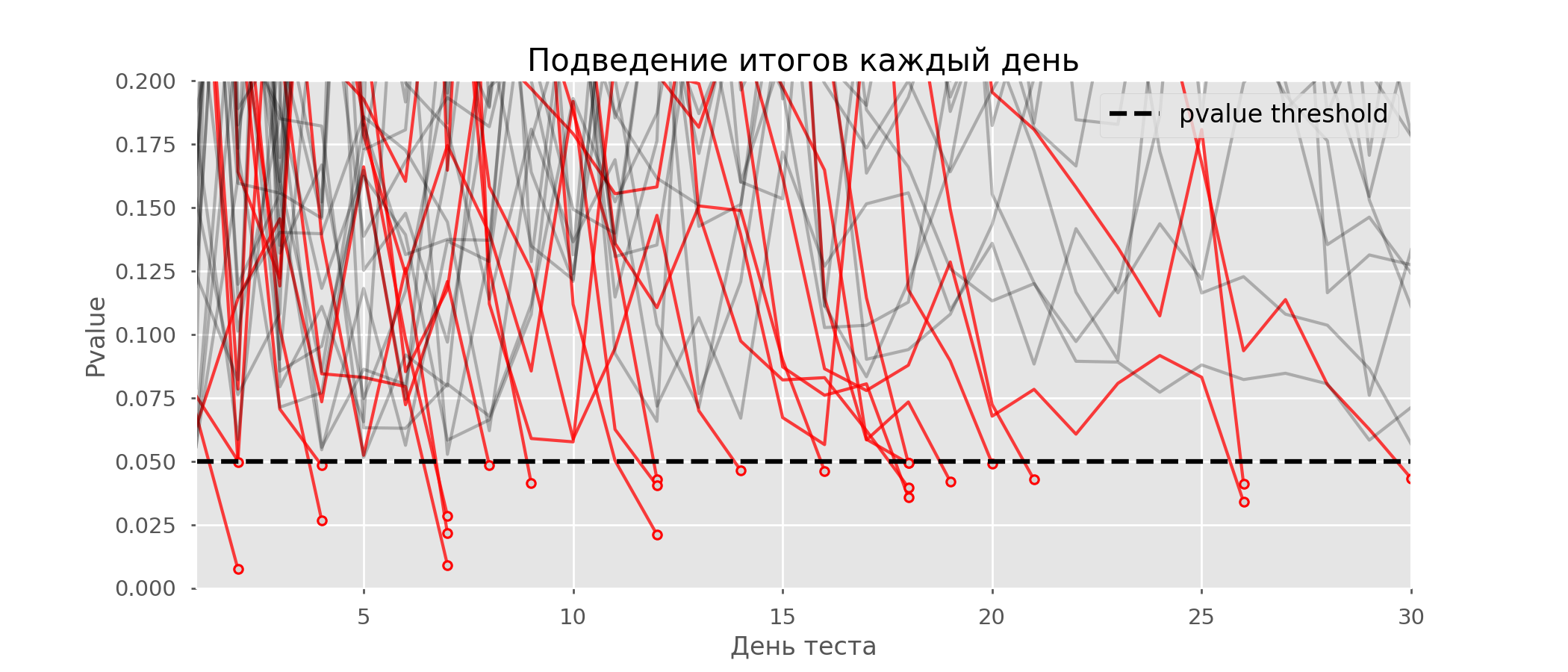
Всего будет 2813 ложноположительных тестов из 10 тысяч, или 28%. Понятно, что такая схема нежизнеспособна.
Хоть проблема подглядывания — это частный случай множественного тестирования, применять стандартные поправки (Бонферрони и другие) здесь не стоит, потому что они окажутся излишне консервативными. На графике ниже — доля ложноположительных результатов в зависимости от количества тестируемых групп (красная линия) и количества подглядываний (зелёная линия).
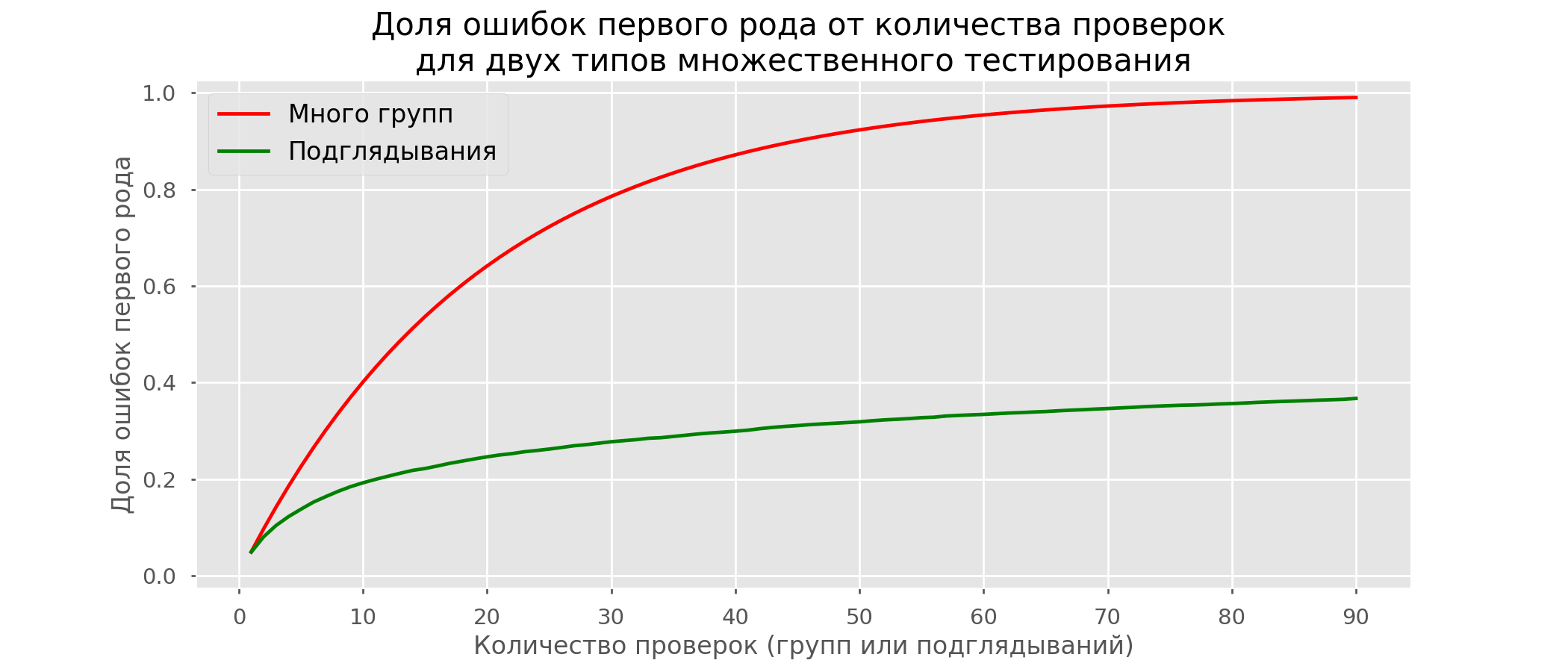
Хотя на бесконечности и в подглядываниях мы вплотную приблизимся к 1, доля ошибок растёт гораздо медленнее. Это объясняется тем, что сравнения в этом случае независимыми уже не являются.
Байесовский подход и проблема подглядывания
Можно встретить мнение, что Байесовский подход к анализу A/B-тестов избавляет от проблемы подглядывания. Это не так, хотя и его можно настроить соответствующим образом. Отличную статью с дополнительными материалами можно почитать здесь.
Методы досрочного завершения теста
Есть варианты тестирования, позволяющие досрочно принять тест. Расскажу о двух из них: с постоянным уровнем значимости (поправка Pocock’a) и зависимым от номера подглядывания (поправка O'Brien-Fleming’a). Строго говоря, для обеих поправок нужно заранее знать максимальный срок теста и количество проверок между запуском и окончанием теста. Причём проверки должны происходить примерно через равные промежутки времени (или через равные количества наблюдений).
Pocock
Метод заключается в том, что мы подводим итоги тестов каждый день, но при сниженном (более строгом) уровне значимости. Например, если мы знаем, что сделаем не больше 30 проверок, то уровень значимости надо выставить равным 0.006 (подбирается в зависимости от количества подглядываний методом Монте-Карло, то есть эмпирически). На нашей симуляции получим 4% ложноположительных исходов — видимо, порог можно было увеличить.

Несмотря на кажущуюся наивность, некоторые крупные компании пользуются именно этим способом. Он очень прост и надёжен, если вы принимаете решения по чувствительным метрикам и на большом трафике. Например, в «Авито» по умолчанию уровень значимости принят за 0.005.
O'Brien-Fleming
В этом методе уровень значимости изменяется в зависимости от номера проверки. Надо заранее определить количество шагов (или подглядываний) в тесте и рассчитать уровень значимости для каждого из них. Чем раньше мы пытаемся завершить тест, тем более жёсткий критерий будет применён. Пороговые значения статистики Стьюдента
Код для воспроизведения коэффициентов
from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score
import matplotlib.pyplot as plt
# datapoints from https://www.aarondefazio.com/tangentially/?p=83
total_steps = [
2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 50, 60
]
last_z = [
1.969, 1.993, 2.014, 2.031, 2.045, 2.066, 2.081,
2.107, 2.123, 2.134, 2.143, 2.164, 2.17
]
features = [
[1/t, 1/t**0.5] for t in total_steps
]
lr = LinearRegression()
lr.fit(features, last_z)
print(lr.coef_) # [ 0.33729346, -0.63307934]
print(lr.intercept_) # 2.247105015502784
print(explained_variance_score(lr.predict(features), last_z)) # 0.999894
total_steps_extended = np.arange(2, 80)
features_extended = [ [1/t, 1/t**0.5] for t in total_steps_extended ]
plt.plot(total_steps_extended, lr.predict(features_extended))
plt.scatter(total_steps, last_z, s=30, color='black')
plt.show()
Соответствующие уровни значимости вычисляются через перцентиль
perc = scipy.stats.norm.cdf(Z)
pval_thresholds = (1 − perc) * 2
На тех же симуляциях это выглядит так:

Ложноположительных результатов получилось 501 из 10 тысяч, или ожидаемые 5%. Обратите внимание, что уровень значимости не достигает значения в 5% даже в конце, так как эти 5% должны «размазаться» по всем проверкам. В компании мы пользуемся именно этой поправкой, если запускаем тест с возможностью ранней остановки. Прочитать про эти же и другие поправки можно по ссылке.
Метод Optimizely
Метод Optimizely хорош тем, что позволяет вообще не фиксировать дату окончания теста, а требуемый уровень значимости рассчитывается на каждый момент времени как функция от количества наблюдений в тесте. Интуитивно лично мне их метод нравится меньше, так как в нём жёсткость критерия увеличивается по ходу теста. То есть она минимальна в первые дни, когда случайный шум оказывает наибольшее влияние на метрики. В методе O'Brien-Fleming’a ситуация противоположная.
Калькулятор A/B-тестов
Специфика нашего продукта такова, что распределение любой метрики очень сильно меняется в зависимости от аудитории теста (например, номера класса) и времени года. Поэтому не получится принять за дату окончания теста правила в духе «тест закончится, когда в каждой группе наберётся 1 млн пользователей» или «тест закончится, когда количество решённых заданий достигнет 100 млн». То есть получится, но на практике для этого надо будет учесть слишком много факторов:
- какие классы попадают в тест;
- тест раздаётся на учителей или учеников;
- время учебного года;
- тест на всех пользователей или только на новых.
Тем не менее, в наших схемах A/B-тестирования всегда нужно заранее фиксировать дату окончания. Для прогноза продолжительности теста мы разработали внутреннее приложение — калькулятор A/B-тестов. Основываясь на активности пользователей из выбранного сегмента за прошлый год, приложение рассчитывает срок, на который надо запустить тест, чтобы значимо зафиксировать аплифт в X% по выбранной метрике. Также автоматически учитывается поправка на множественную проверку и рассчитываются пороговые уровни значимости для досрочной остановки теста.
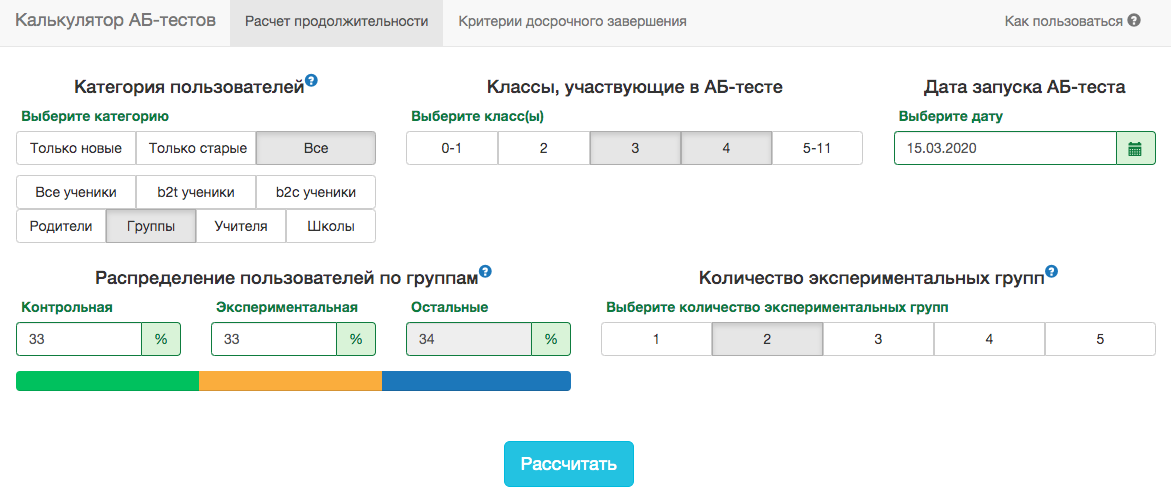
Все метрики у нас рассчитываются на уровне объектов теста. Если метрика — количество решённых задач, то в тесте на уровне учителей это будет сумма решённых задач его учениками. Так как мы пользуемся критерием Стьюдента, можно заранее рассчитать нужные калькулятору агрегаты по всем возможным срезам. Для каждого дня со старта теста нужно знать количество людей в тесте
Далее легко получить значения p-value на каждый день:
pvalue = (1 − scipy.stats.norm.cdf(ttest_stat_value)) * 2
Зная p-value и уровень значимости с учетом всех поправок на каждый день теста, для любой продолжительности теста можно рассчитать минимальный аплифт, который можно задетектировать (в англоязычной литературе — MDE, minimal detectable effect). После этого легко решить обратную задачу — определить количество дней, необходимое для выявления ожидаемого аплифта.
Заключение
В качестве заключения хочу напомнить основные посылы статьи:
- Если вы сравниваете средние значения метрики в группах, скорее всего, вам подойдёт критерий Стьюдента. Исключение — экстремально малые размеры выборки (десятки наблюдений) или аномальные распределения метрики (на практике я таких не встречал).
- Если в тесте несколько групп, пользуйтесь поправками на множественное тестирование гипотез. Подойдёт простейшая поправка Бонферрони.
- Сравнения по дополнительным метрикам или срезам групп тоже подвержены проблеме множественного тестирования.
- Выбирайте дату завершения теста заранее. Вместо даты также можно зафиксировать количество наблюдений в группе.
- Не подводите итоги теста раньше этой даты. Это можно делать, только если вы заранее решили пользоваться методами, подразумевающими досрочное завершение, например, методом O'Brien-Fleming.
- Когда вносите изменения в схему A/B-тестирования, всегда проверяйте её жизнеспособность A/A-тестами.
Несмотря на всё вышенаписанное, бизнес и здравый смысл не должны страдать в угоду математической строгости. Иногда можно выкатить на всех функционал, не показавший значимого прироста в тесте, какие-то изменения неизбежно происходят вообще без тестирования. Но если вы проводите сотни тестов в год, их аккуратный анализ особенно важен. Иначе есть риск, что количество ложноположительных тестов будет сравнимо с реально полезными.