Поскольку я столкнулся с существенными затруднениями в поисках объяснения механизма обратного распространения ошибки, которое мне понравилось бы, я решил написать собственный пост об обратном распространении ошибки реализовав алгоритм Word2Vec. Моя цель, — объяснить сущность алгоритма, используя простую, но нетривиальную нейросеть. Кроме того, word2vec стал настолько популярным в NLP сообществе, что будет полезно сосредоточиться на нем.
Данный пост связан с другим, более практическим постом который рекомендую прочитать, в нем рассматривается непосредственная реализация word2vec на языке python. В данном же посте мы сосредоточимся в основном на теоретической части.
Начнем с вещей которые необходимы для настоящего понимания обратного распространения. Помимо понятий из машинного обучения, таких как, функция потерь и градиентный спуск, пригодятся еще два компонента из математики:
- линейная алгебра (в частности матричное умножение)
- правило цепочки дифференцирования функций от многих переменных
Если вам знакомы эти понятия, то дальнейшие рассуждения окажутся простыми. Если же вы еще не освоили их, то все равно сможете понять основы обратного распространения.
Сперва я хочу дать определение понятию обратного распространения, если смысл будет недостаточно понятен, он будет раскрыт подробнее в следующих пунктах.
1. Что такое алгоритм обратного распространения
В рамках нейронной сети, единственными параметрами участвующими в обучении сети, то есть минимизации функции потерь, являются веса (здесь имею в виду веса в широком смысле, относя к ним и смещения). Веса изменяются на каждой итерации, пока мы не приблизимся к минимуму функции потерь.
В таком контексте, обратное распространение — это эффективный алгоритм нахождения оптимальных весов нейронной сети, то есть тех, которые оптимизируют функцию потерь.
Стандартный способ нахождения этих весов, применение алгоритма градиентного спуска, который подразумевает нахождение частных производных функции потерь по всем весам.
Для тривиальных задач в которых всего две переменных, легко представить как работает градиентный спуск, если вы посмотрите на рисунок, то увидите трехмерный график функции потерь, как функции весов w1 и w2.

Рисунок 1. Визуальное объяснение алгоритма градиентного спуска.
Вначале мы не знаем оптимальные значения, то есть не знаем какие значения w1 и w2 минимизируют функцию потерь.
Допустим, мы начинаем с красной точки. Если мы знаем как изменяется функция потерь при изменении весов, то есть если мы знаем производные и
, то мы можем сдвинуть красную точку ближе к минимуму функции потерь, которая представлена на графике синей точкой. Шаг сдвига определяется параметром
, который обычно называется параметром обучения.
2. Word2Vec
Задача алгоритма word2vec, найти эмбеддинги слов в заданном текстовом корпусе, другими словами, это методика поиска представлений слов в низкой размерности. Как следствие, когда мы говорим о word2vec, мы обычно говорим о приложениях NLP.
Например, модель word2vec обученная со скрытым слоем размерности [N, 3], где N -количество слов в словаре, даст трехмерные эмбеддинги слов. Это значит что, например, слово 'квартира', будет представлено трехмерным вектором действительных чисел, который будет близок (воспринимайте это как Евклидову метрику), к представлению аналогичного слова, такого как 'дом'. Другими словами, word2vec это техника отображения слов в числа.
В контексте word2vec используются две основные модели: мешок слов (CBOW) и скипграммы (skip-gram). Сначала мы рассмотрим простейшую модель, CBOW, с окном из одного слова, затем перейдем к окну из нескольких слов и наконец рассмотрим модель skip-gram.
По мере продвижения я покажу несколько небольших примеров с текстом состоящим всего из нескольких слов. Однако имейте в виду, что обычно woed2vec тренируется с миллиардами слов.
3. Простая модель CBOW
В CBOW модели задача состоит в поиске слова по его контексту. В простейшем случае когда контекст слова представлен одним словом, нейронная сеть будет выглядеть так:
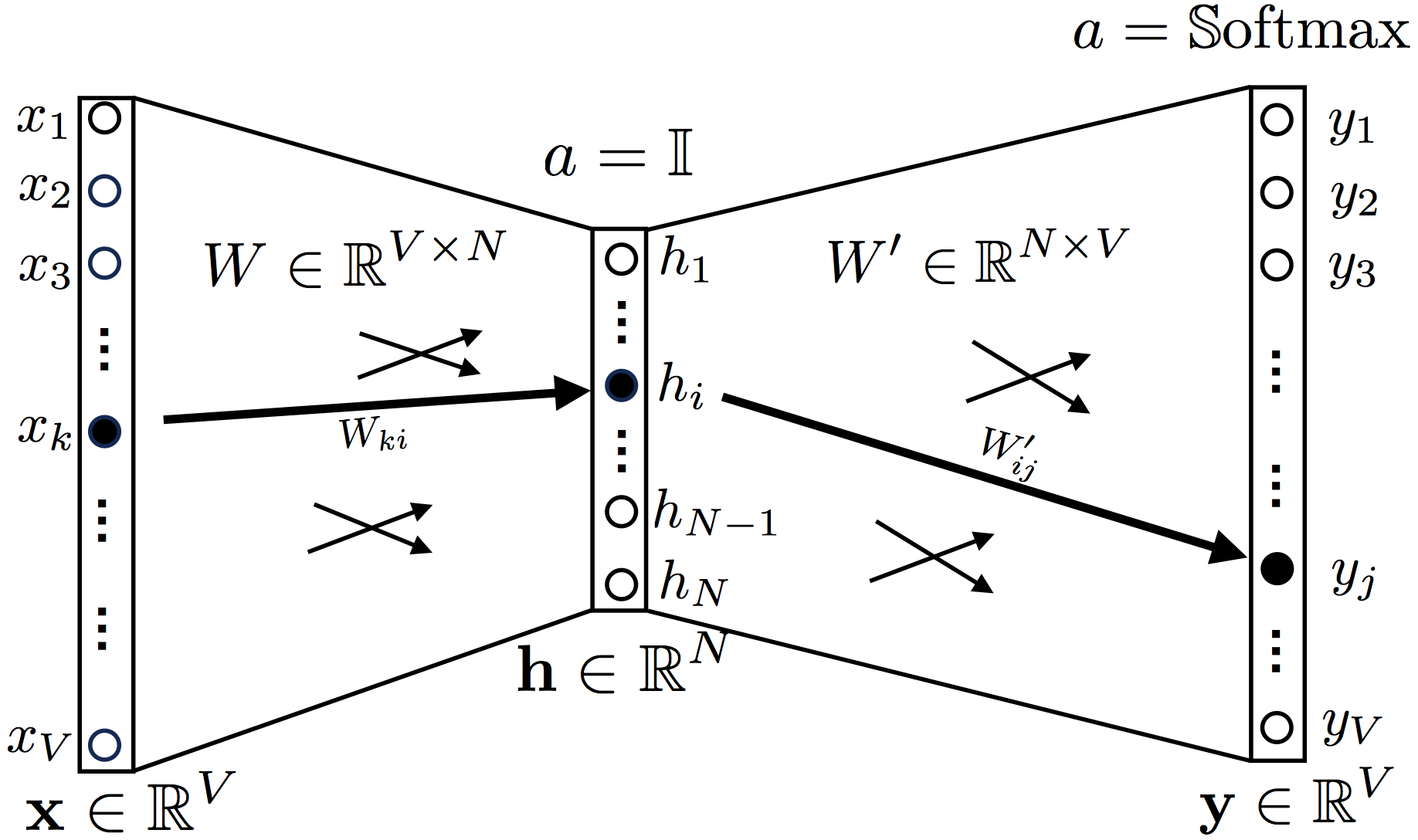
Рисунок 2. Топология модели Continuous Bag-of-Words модели с контекстом из одного слова
Один входной слой, один скрытый слой и выходной слой, функция активации скрытого слоя
a = 1 (identity function, или функция линейной активации, хотя последнее неправильно).
В качестве функции активации выходного слоя используется Softmax.
Входной слой представлен one hot encoding вектором, длина которого совпадает с размером массива слов, все элементы данного вектора равны нулю, кроме элементов, индексы которых совпадают с индексами слов из контекста, по данным индексам значения вектора равны 1.
Пример: словарь ['мама', 'мыла', 'раму', 'маша', 'ела', 'кашу']
OneHot('маша') = [0, 0, 0, 1, 0, 0]
OneHot(['мама', 'маша']) = [1, 0, 0, 1, 0, 0]
OneHot(['мама', 'ела', 'кашу']) = [1, 0, 0, 0, 1, 1]
Перейдем к весам, весовые коэффициенты между входным и скрытым слоем представлены матрицей W размера , матрица между скрытым и выходным слоем
размером
, где V — размер словаря, N — размер эмбеддинг вектора (то есть, те вектора которые и пытается найти word2vec)
Выходной вектор y сравниваем с ожидаемым вектором t, чем они ближе, тем выше эффективность нейронной сети, и, соответственно, меньше функция потерь.
Если на текущем этапе что то звучит непонятно, то пример ниже должен прояснить ситуацию.
Предположим, мы хотим обучить word2vec следующим текстом:
"I like playing football"
Мы решаем обучить модель CBOW с одним контекстным словом как на рисунке (2) выше.
Учитывая текст который у нас есть, наш словарь будет состоять из 4 слов, соответственно V=4, также установим что скрытый слой будет иметь два нейрона, то есть N=2, наша нейросеть будет выглядеть так:
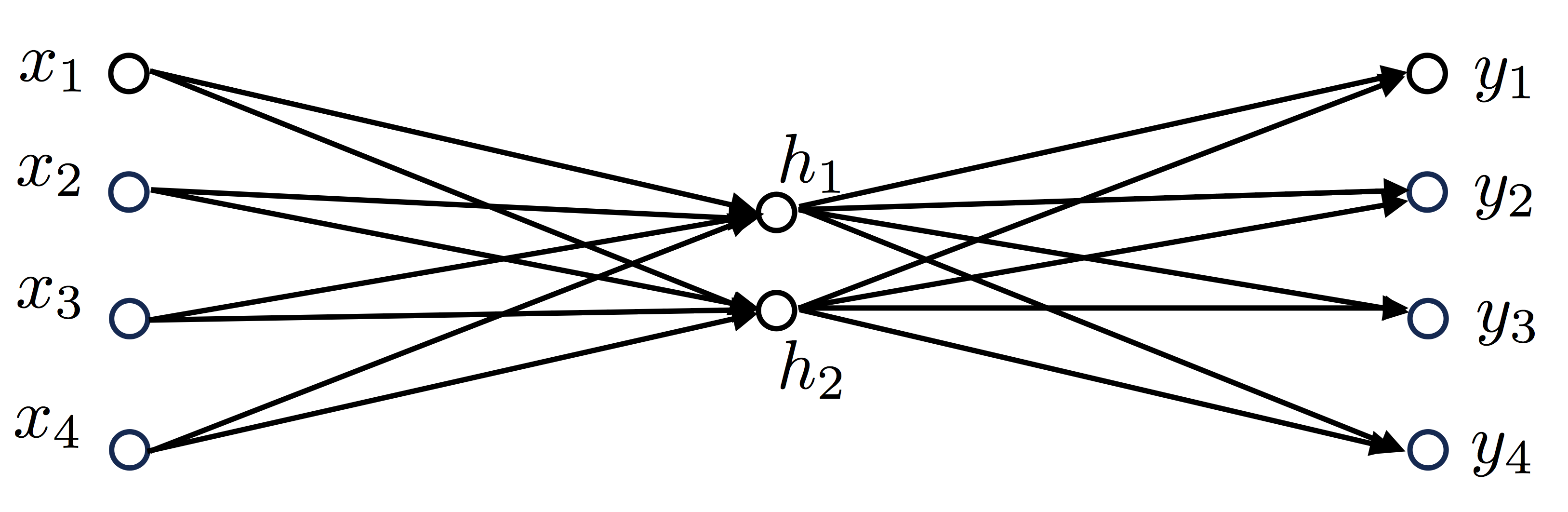
Со словарём:
Далее мы определяем как выбирать 'целевое' и 'контекстное' слово, и мы можем построить наши обучающие примеры двигаясь окном по тексту. Например:

Тогда обучающие примеры будут выглядеть так:
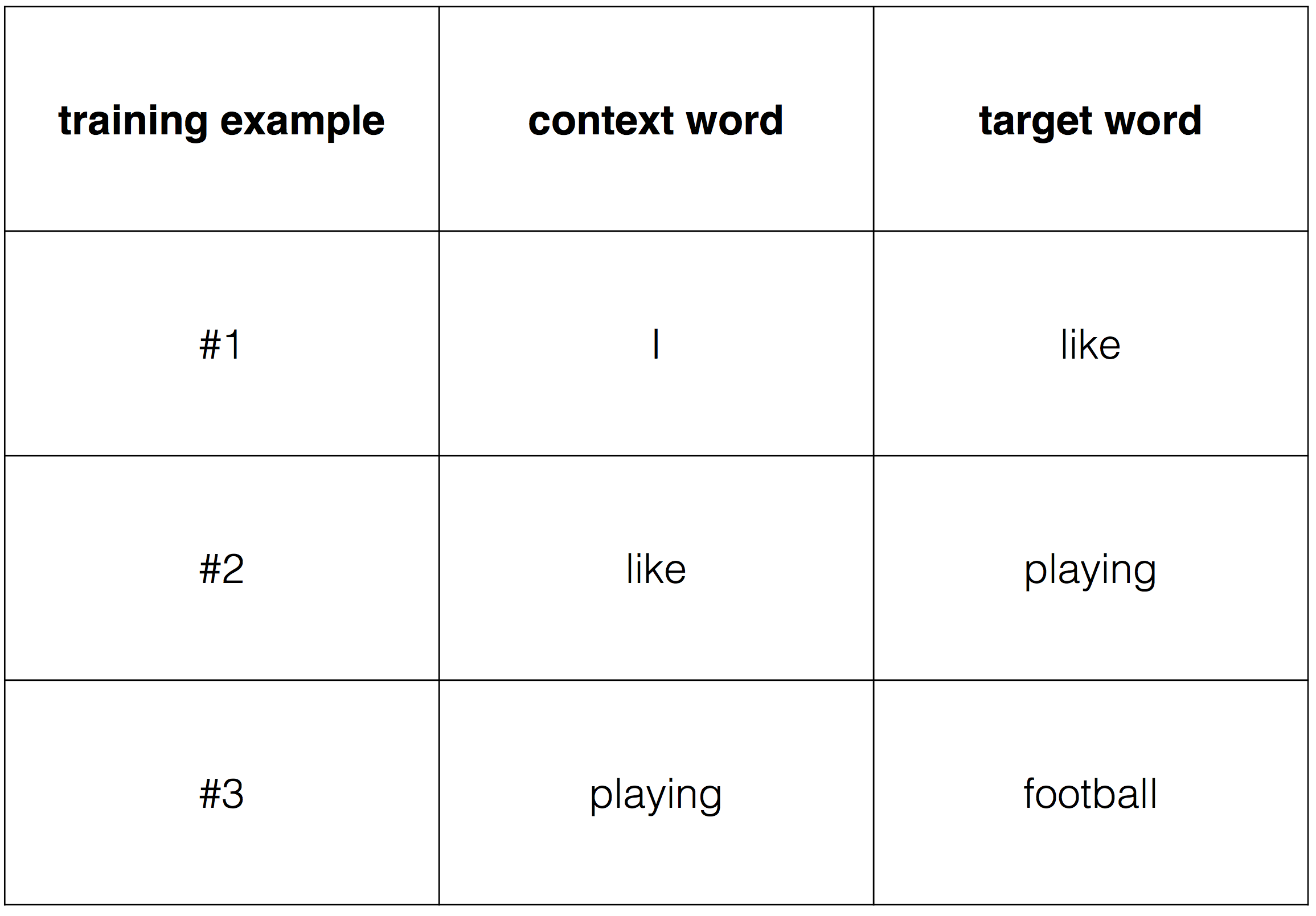
Чтобы передать эти данные в алгоритм понадобится преобразовать их в числа, для чего используем one-hot encoding.
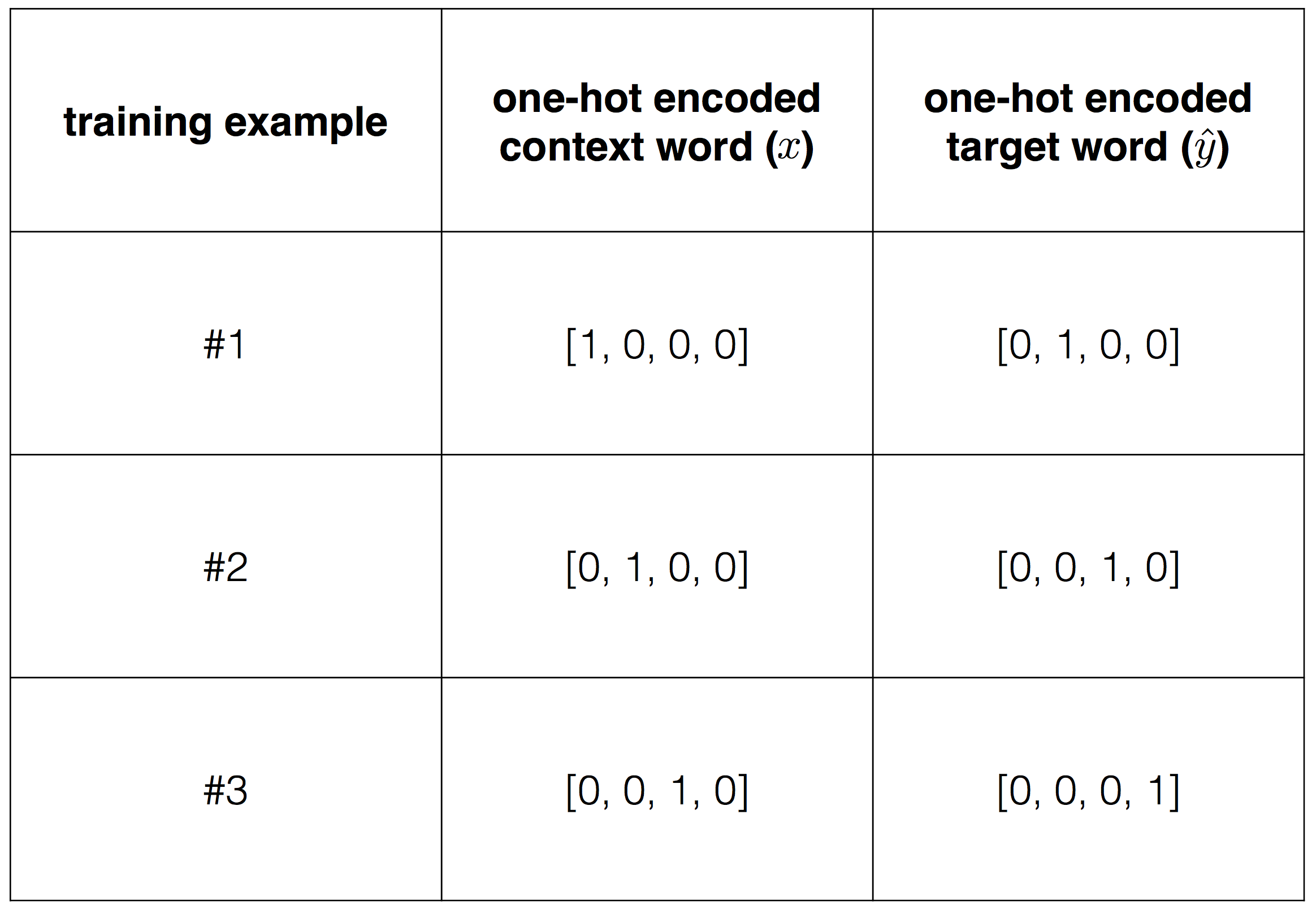
На данный момент, мы хотим обучить нашу модель, находя веса, которые минимизируют функцию потерь. Это соответствует нахождению весов, которые с учетом вектора контекста могут с высокой точностью предсказать, что является соответствующим целевым словом.
3.1 Функция потерь (Loss function)
Исходя из топологии на рисунке 1, давайте запишем как посчитать значения скрытого и выходного слоев, при входе x:
где, h — сумма на скрытом слое, u — сумма на выходном слое, y — выход сети.
Теперь, предположим, мы обучаем модель по паре целевое слово, контекстное слово (wt, wc). Целевое слово представляет собой идеальное предсказание нейронной сети, в виде onehot encoding вектора.
Функция потерь должна будет оценить выходной слой, относительно onehot вектора wt (целевого слова).
Поскольку значения softmax можно интерпретировать как условные вероятности целевого слова, то учитывая контекстное слово функцию потерь можно записать в следующем виде:
, где j* — ожидаемая позиция правильно предсказанного слова.
Добавление функции логарифма является стандартным подходом. Из данного выражения мы получаем уравнение (1):
Функция потерь максимизирует вероятность предсказания правильного слова исходя из заданного контекста.
Вернемся к предыдущему примеру предложения "I like play football", предположим мы обучаем модель по первой записи обучающих данных, с контекстным словом "I" и целевым словом "like", в идеале веса сети должны быть такими, чтобы при вводе — что соответствует слову "I", результат работы был близок к
, что соответствует слову "like".
Стандартный подход к инициализации весов word2vec, использование нормального распределения. Примем начальное состояние весов матрицы W размером
И начальное состояние весов матрицы размером
Для обучающих данных "I like" мы получаем:
Затем
И наконец
На этом этапе функция потерь будет отрицательным логарифмом второго элемента , или
Также, мы могли бы рассчитать ее при помощи уравнения (1):
Теперь, прежде чем перейти к следующему обучающему примеру "like play", мы должны изменить веса нейросети, как это сделать расскажет следующий пункт про обратное распространение.
3.2 Алгоритм обратного распространения для модели CBOW
Теперь, имея в наличии функцию потерь, мы хотим найти веса W и W` которые ее минимизируют. В терминах машинного обучения, мы хотим чтобы модель обучилась.
В первом разделе мы уже обсудили что в мире нейронный сетей эта проблема решается использованием градиентного спуска. На рисунке (1) показано как применить этот метод и обновить матрицы весов W и W`. Нам нужно найти производные и
Я считаю что самый простой способ понять как это сделать, это записать соотношения между функцией потерь и матрицами весов. Глядя на уравнение (1) ясно что функция потерь зависит от весов W и W`, через переменную u=[u1, ...., uV], или
Получить производные можно из правила цепочки для функций многих переменных:
и
И это большая часть алгоритма обратного распространения, на данный момент нам просто нужно определить уравнения (2) и (3) для нашего случая.
Начнем с уравнения (2), обратите внимание что вес Wij, относится к матрице W, и соединяет нейрон i в скрытом слое с нейроном j в выходном слое, и соответственно оказывает влияние только на выход uj (соответственно и на yj).
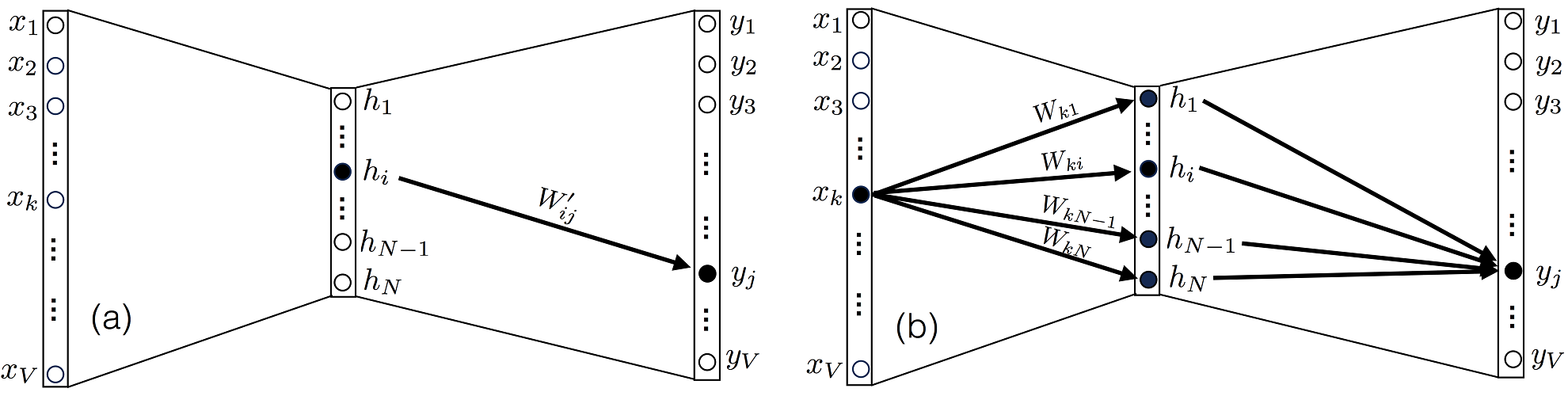
Рисунок 3. (a) Выходной узел зависит от общего узла
скрытого слоя только через элемент
матрицы
. (b) Но кроме того, этот же выходной узел зависит от общего входного узла
через N элементов
матрицы W.
Следовательно, среди всех производных , только одна, где k=j, будет отличаться от 0.
Уравнение (4):
Давайте посчитаем , уравнение (5):
, где — дельта Кронекера, функция двух целых переменных, которая равна 1, если они равны, и 0 в противном случае.
В уравнении (5) мы ввели вектор e размерности N (размер словаря), который мы используем чтобы снизить сложность обозначений, этот вектор представляет собой разницу между полученным и ожидаемым результатом, то есть это вектор ошибок предсказания.
Для второго члена правой части уравнения (4) мы получим уравнения (6):
После подставновки уравнений (5) и (6) в уравнение (4) мы получим уравнение (7):
Мы можем найти выполнить аналогичное упражнение для поиска производной , однако на этот раз отметим что после задания входа Xk, выход yj нейрона j зависит от всех элементов матрицы W соединенных со входом, как видно на рисунке 3(b). Поэтому мы должны оценивать все элементы в сумме. Прежде чем перейти к оценке
, полезно перезаписать выражение для элемента uk из вектора u как:
Из этого уравнения легко вывести , поскольку единственный выживший член производной будет с индексами l=i и m=j, или же в виде уравнения (8):
Наконец применив уравнения (5) и (8) мы получим результат, уравнение (9):
Мы можем упростить запись уравнений. (7) и (9) используя векторную нотацию. Сделав это мы получим для уравнения (7)
Где символ ⊗ обозначает векторное произведение.
Для уравнения (9) мы получим:
3.3 Градиентный спуск на основе полученных выше результатов
Теперь, когда у нас есть уравнения (7) и (9), у нас есть все необходимое для реализации одной итерации обучения нейросети на базе алгоритма обратного распространения ошибки, применяя градиентный спуск. Каждая итерация должна немного приближать к минимуму функцию потерь. После задания скорости обучения , мы можем обновить наши веса следующим образом:
3.4 Итерация алгоритма
Все описанное выше является всего лишь одним маленьким шагов всего процесса оптимизации. В частности, до этого момента мы обучали нашу нейросеть всего на одном тренировочном примере. Чтобы завершить первый проход, мы должны применить все обучающие примеры. Сделав это, мы пройдем одну эпоху обучения. После чего нам нужно будет повторять цикл обучения, пройдя достаточное количество эпох, пока изменения функции потерь не станут незначительными, после чего можно будет остановиться и считать нейросеть обученной.
4. Алгоритм обратного распространения для контекста из нескольких слов в модели CBOW
Мы уже знаем как работает алгоритм обратного распространения для модели CBOW с одним словом на входе. Теперь увеличим сложность и добавим в контекст несколько слов. Рисунок (4) показывает как выглядит нейросеть теперь. Вход теперь представляет собой серию OneHot Encoded векторов слов входящих в контекст. Количество слов в контексте является параметром который мы можем задавать при инициализации word2vec. Скрытый слой получает усреднение из всех контекстных слов.

Рисунок 4. Топология модели CBOW с контекстом из нескольких слов
Уравнения модели CBOW с несколькими контекстными словами являются обобщением уравнений модели CBOW с одним контекстным словом.
Обратите внимание, что для удобства мы ввели определение 'усредненный' входной вектор
Как и прежде, чтобы применить алгоритм обратного распространения нам нужно выписать функцию потерь и выписать ее зависимости. Функция потерь выглядит также как и раньше:
Снова выпишем уравнения по правилу цепочки, аналогично предыдущим:
и
Производные функции потерь по весам такие же как для модели CBOW с одним словом на входе, с единственным отличием, что мы заменим входной вектор из одного слова на усредненный вектор из слов контекста. Выведем эти уравнения начиная с производной по
Теперь запишем производную по :
Подведя итог имеем следующее:
и
Перепишем уравнения (17) и (18) в записи для векторов.
Уравнение (17) примет вид:
Для уравнения (18):
Еще раз, обратите внимание что уравнения идентичны уравнениям в модели CBOW для контекста из одного слова.
Оператор ⊗ обозначает векторное произведение.
5. Алгоритм обратного распространения для модели Skip-gram
Данная модель по сути обратна модели CBOW, на вход подается центральное слово, на выходе предсказывается его контекст. Полученная нейросеть выглядит следующим образом:
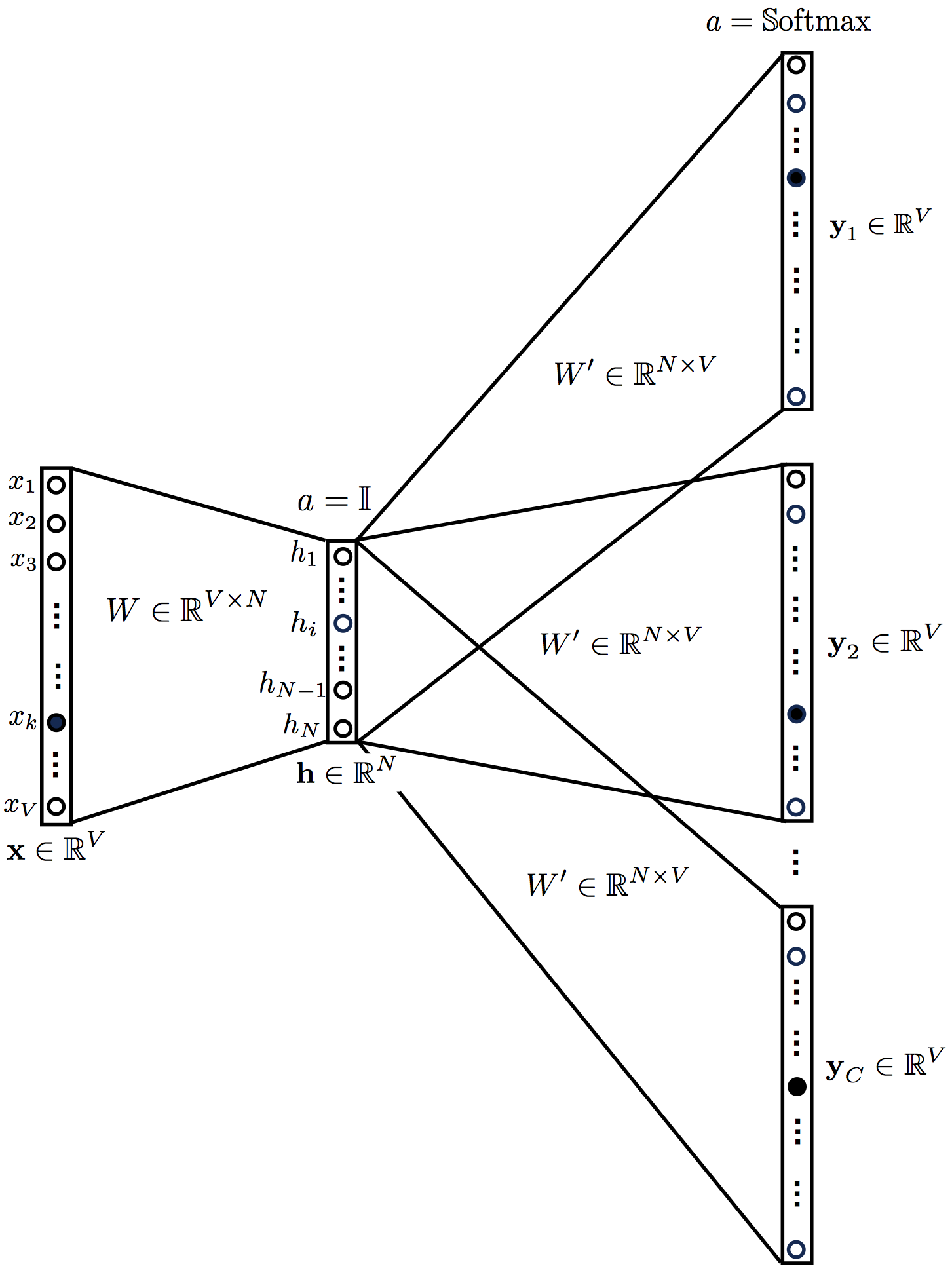
Рисунок 5.Топология Skip-gram модели.
Уравнения skip-gram модели следующие:
Обратите внимание что выходные вектора (как и вектор ) идентичны,
. Функция потерь выглядит следующим образом:
Для модели skip-gram функция потерь зависит от переменных
через:
Соответственно правило цепочки выглядит так:
и
Посчитаем , получим:
Аналогично модели CBOW получаем:
Производная по самая сложная, но выполнимая:
Подведя итог, для модели skip-gram мы имеем:
и
Векторизованная версия уравнения (21):
Уравнение (22):
6. Что дальше
Мы подробно рассмотрели как работает алгоритм обратного распространения в случае word2vec. Однако рассмотренная реализация неэффективна для больших текстовых корпусов. В оригинальной статье [2] применяются некоторые трюки для преодоления этих проблем (иерархический softmax, negative sampling), однако я не буду на них останавливаться подробно. Вы можете найти подробное описание по ссылке [1].
Несмотря на вычислительную неэффективность реализации описанной здесь, она содержит всё необходимое для обучения нейронных сетей word2vec.
Следующим шагом будет реализация этих уравнений на вашем любимом языке программирования. Если вам нравится Python, я уже реализовал эти уравнения в моем следующем посте.
Надеюсь увидеть вас там!
Дополнительные ссылки
[1] X. Rong, word2vec Parameter Learning Explained, arXiv:1411.2738 (2014).
[2] T. Mikolov, K. Chen, G. Corrado, J. Dean, Efficient Estimation of Word Representations in Vector Space, arXiv:1301.3781 (2013).