Гипотеза о простых числах-близнецах – один из самых важных и сложных вопросов математики. Двое математиков решили параллельную версию этой задачи для небольших числовых систем.

7 сентября два математика опубликовали доказательство варианта одной из известнейших открытых задач математики. Полученный результат открывает новый фронт в изучении гипотезы о простых числах-близнецах, терзающей математиков вот уже более ста лет, и связанной с некоторыми из глубочайших свойств арифметики.
«Мы давно уже буксовали и у нас заканчивались идеи по этой задаче, поэтому естественный восторг вызывает появление у кого-либо новых идей», — сказал Джеймс Майнард, математик из Оксфорда.
Гипотеза о простых числах-близнецах касается пар простых чисел, отличающихся на 2. Близнецами являются числа 5 и 7. И 17 и 19. Гипотеза утверждает, что таких пар среди натуральных чисел существует бесконечное множество. За последнее десятилетие математики добились существенного прогресса, но до полного решения задачи им ещё очень далеко.
Авторы нового доказательства, Уил Савин из Колумбийского университета и Марк Шустерман из Висконсинского университета в Мэдисоне, доказали гипотезу для менее крупного, но всё же заметного математического мира. Они доказали её справедливость в случае конечной числовой системы, в которой есть лишь несколько чисел.
Такие числовые системы называются «конечными полями». Несмотря на их малый размер, они сохраняют множество математических свойств, присущих бесчисленным целым числам. Математики пытаются искать ответы на вопросы арифметики в конечных полях, и надеются транслировать эти результаты на все целые числа.
«Конечная мечта, пусть и немного наивная, заключается в том, что хорошее понимание свойств конечного поля может пролить свет на мир целых чисел», — сказал Майнард.
Кроме доказательства гипотезы о простых числах-близнецах Савин и Шустерман нашли ещё более удивительный результат, касающийся поведения простых чисел в небольших числовых системах. Они доказали, с какой именно частотой простые числа-близнецы появляются на небольших интервалах – и этот результат даёт возможность чрезвычайно точно контролировать такое явление, как простые числа-близнецы. Математики мечтают достичь сходных результатов и с обычными числами; они исследуют новое доказательство в поисках идей, применимых к простым числам на числовой прямой.
Новый вид простых чисел
Самое известное предсказание гипотезы о простых числах-близнецах заключается в наличии бесконечно большого количества пар чисел, различающихся на 2. Однако это утверждение более общее. Оно говорит о том, что существует бесконечное количество простых чисел, различающихся на 4 (к примеру, 3 и 7), или на 14 (293 и 307), или на любое заданное вами число.
Альфонс де Полиньяк сделал это предположение в его современном виде в 1849 году. За последовавшие 160 лет математики не сильно продвинулись с ним. Однако в 2013 году лёд тронулся, или, по крайней мере, серьёзно треснул. В тот год Чжан Итан доказал наличие бесконечно большого количества пар простых чисел, отличающихся друг от друга не более, чем на 70 млн. В следующем году другие математики, включая Мэйнарда и Терри Тао, серьёзно уменьшили этот разрыв. Текущим рекордом служит доказательство существования бесконечно большого количества пар простых чисел, отличающихся друг от друга не более, чем на 246.
Однако после этого прогресс утих. Математики понимают необходимость совершенно новой идеи для полного решения данной задачи. И конечные числовые системы – неплохое место для поисков этой идеи.
Чтобы построить конечное поле, сначала нужно извлечь конечное подмножество чисел из натуральных. Можно, к примеру, взять первые пять чисел (или любое простое количество). И вместо того, чтобы, как обычно, представлять числа на числовой линии, представьте новую числовую систему в виде циферблата.
Арифметика, как вы могли догадаться, начинает работать в замкнутом пространстве. Чему будет равно 4 + 3 в конечной числовой системе, состоящей из пяти элементов? Начнём с 4, отсчитаем три деления по часовой стрелке, и придём к 2. Вычитание, умножение и деление работают сходным образом.

Но только тут есть подвох. На конечных полях не имеет смысла обычное определение простого числа. На конечном поле любое число делится на любое другое. К примеру, 7 обычно не делится на 3. Но на конечном поле из пяти элементов – делится. Всё потому, что на этом конечном поле число 7 эквивалентно числу 12 – они оба заканчиваются на отметке 2 циферблата. Поэтому 7 разделить на 3 даст то же самое, что и 12 разделить на 3 – а 12, делённое на 3, даст 4.
Поэтому гипотеза простых чисел-близнецов для конечных полей относится к простым многочленам – таким математическим выражениям, как, например, x2 + 1.
Допустим, к примеру, что ваше конечное поле содержит числа 1, 2 и 3. Эти числа будут коэффициентами многочлена в этом конечном поле, а «простым» многочленом будет такой, который нельзя разложить на множители-многочлены. Поэтому x2 + x + 2 будет простым, поскольку его нельзя разложить на множители, а x2 — 1 не будет: это произведение (x + 1) и (x − 1).
Определив простые многочлены, естественно задать вопрос о простых многочленах-близнецах – парах многочленов, являющихся простыми, и отличающихся на фиксированное значение. К примеру, многочлен x2 + x + 2 простой, как и x2 + 2x + 2. Отличаются они на x.
Гипотеза о простых многочленах-близнецах для конечных полей говорит о существовании бесконечно большого количества пар простых многочленов-близнецов, отличающихся не просто на x, а на любое значение.
Аккуратные разрезы
Понятия конечных полей и простых многочленов могут показаться притянутыми за уши, и бесполезными для изучения свойств чисел. Но они похожи на симулятор урагана – вселенную в себе, дающую идеи по поводу явлений, происходящем в большом мире.
«Между целыми числами и многочленами существует древняя аналогия, позволяющая преобразовывать потенциально крайне сложные задачи, связанные с целыми числами, в задачи, связанные с многочленами, которые тоже потенциально сложны, но, возможно, легче поддаются решению», — сказал Шустерман.
Конечные поля приобрели известность в 1940, когда Андре Вейль, разработал точный способ трансляции арифметики небольших числовых систем в арифметику целых чисел. Вейль использовал эту связь с потрясающими результатами. Он доказал, возможно, самую важную проблему в математике – гипотезу Римана – для случая с набором кривых над конечными полями (эта задача известна под именем геометрической гипотезы Римана). Это доказательство, вместе с набором дополнительных гипотез Вейля сделало конечные поля богатым ландшафтом для математических открытий.
Ключевой идеей Вейля было то, что на конечных полях геометрические техники можно использовать для поиска ответов на вопросы по поводу чисел. «Это особенность конечных полей. Многие задачи, которые вы хотите решить, можно перефразировать геометрически», — сказал Шустерман.
Чтобы понять, как в таком окружении появляется геометрия, представьте себе каждый многочлен в виде точки в пространстве. Коэффициенты многочлена служат координатами, определяющими его местоположение. Возвращаясь к нашему конечному полю из 1, 2 и 3, многочлен 2x + 3 расположится в точке (2, 3) двумерного пространства.
Но даже в простейшем конечном пространстве есть бесконечное множество многочленов. Можно создавать более сложные многочлены, увеличивая показатель самой большой экспоненты, или степень выражения. В нашем случае многочлен x2 − 3x − 1 будет представлен точкой в трёхмерном пространстве. А многочлен 3x7 + 2x6 + 2x5 − 2x4 − 3x3 + x2 − 2x + 3 будет представлен точкой в восьмимерном пространстве.
В новой работе это геометрическое пространство представляет все многочлены заданной степени для заданного конечного поля. Вопрос превращается в следующий: есть ли способ изолировать все точки, обозначающие простые многочлены?
Стратегия Савина и Шустермана заключается в том, чтобы разделить пространство на две части. В одной части будут все точки, соответствующие многочленам с чётным количеством множителей. В другой – все точки, соответствующие многочленам с нечётным количеством множителей.
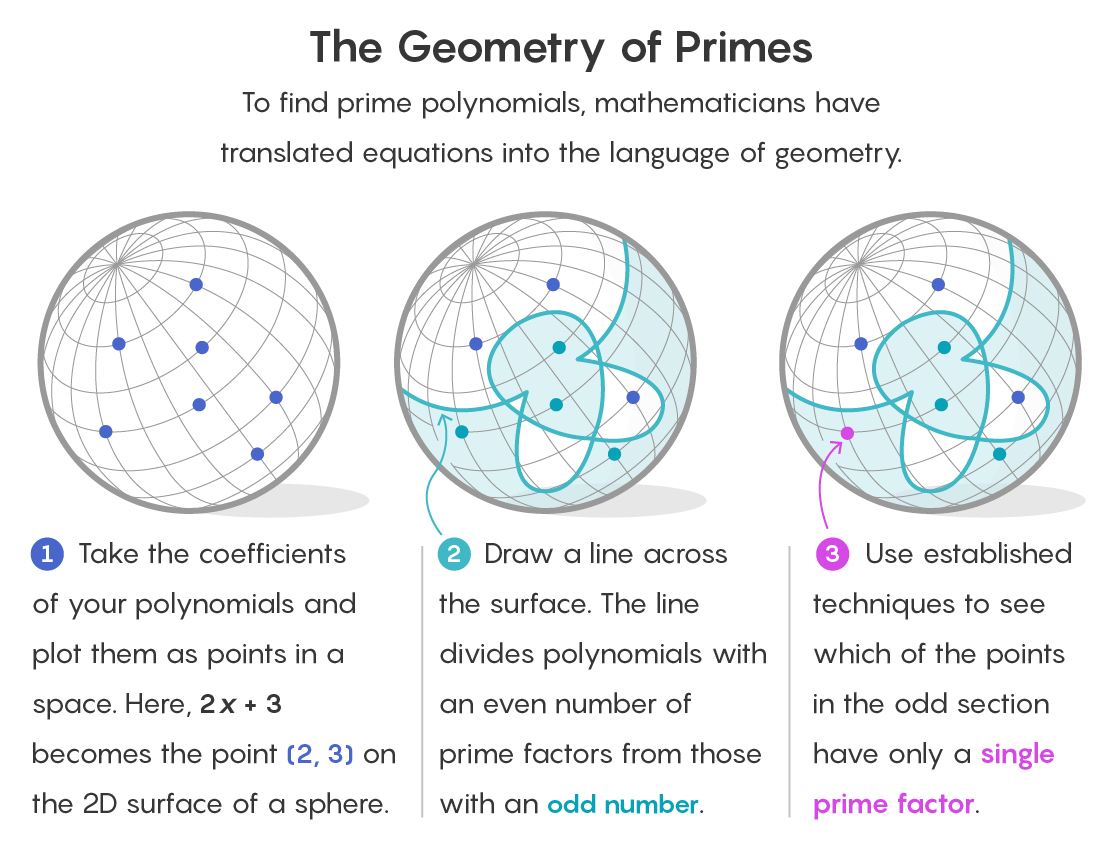
Это уже упрощает задачу. Гипотеза простых многочленов-близнецов для конечных полей относится только к многочленам с одним множителем (точно так же, как у простого числа есть один множитель, оно само). И поскольку число 1 нечётное, часть пространства, содержащего многочлены с чётным числом множителей, можно сразу выбросить.
Трюк состоит в использовании деления. В случае с двумерным объектом, например, поверхностью сферы, его разрезает пополам одномерная кривая – так, как экватор разрезает поверхность Земли. Объект с большим числом измерений всегда можно разрезать объектом с числом измерений, меньшим на единицу.
Но эти формы с меньшим числом измерений, делящие пространство многочленов, вовсе не так элегантны, как экватор. Их рисуют по математической формуле под названием функция Мёбиуса. На вход она принимает многочлен, а на выходе даёт 1, если у многочлена есть чётное количество простых множителей, -1, если у него их нечётное количество, и 0, если он разлагается на одинаковые множители (так, как 16 можно разложить на 2 × 2 × 2 × 2).
Кривые, нарисованные функцией Мёбиуса, гнутся и извиваются, как бешеные, пересекаясь сами с собою во многих местах. Эти места, называемые сингулярностями, особенно тяжело проанализировать (они соответствуют многочленам, раскладываемым на несколько одинаковых простых множителей).
Принципиальной инновацией Савина и Шустермана было то, что они нашли точный способ разрезать петли с меньшим числом измерений на более короткие отрезки. Эти отрезки было легче изучать, чем петли целиком.
Составив каталог многочленов с нечётным количеством простых множителей – а это было самое трудное — Савин и Шустерман столкнулись с задачей определения того, какие из них простые, и какие – близнецы. Для этого они применили несколько формул, используемых математиками для изучения простых чисел среди обычных.
Савин и Шустерман использовали свою технику, чтобы доказать два важных момента касательно простых многочленов на определённых конечных полях.
Во-первых, гипотеза простых чисел-близнецов на конечных полях верна: существует бесконечно много пар простых многочленов-близнецов, отличающихся на любую заданную величину.
Во-вторых, что более важно, эта работа обеспечивает точный подсчёт количества простых многочленов-близнецов, которые можно найти среди многочленов определённого порядка. Это аналогично знанию о том, сколько простых чисел-близнецов есть внутри любого достаточно длинного интервала на числовой прямой – и это просто мечта математиков.
«Это первая работа, дающая количественную аналогию того, что должно быть истинным для целых чисел, и это реально выдающийся результат, — сказал Зив Рудник из Тель-Авивского университета. – До сих пор ничего подобного не было».
Доказательство Савина и Шустермана показывает, как, спустя почти 80 лет после того, как Андре Вейль доказал гипотезу Римана для кривых над конечными полями, математики всё ещё с упорством движутся в эту сторону. Теперь математики, разбирающиеся с гипотезой простых чисел-близнецов, обратятся к работе Савина и Шустермана, и, возможно, она даст им глубокий источник вдохновения.