SemyonSinchenko Mar 27 2019 at 14:17

Neural Quantum States — представление волновой функции нейронной сетью

8 min

5.4K

Райффайзен Банк corporate blog Machine learning *Physics

В этой статье мы рассмотрим необычное применение нейронных сетей в целом и ограниченных машин Больцмана в частности для решения двух сложных задач квантовой механики — поиска энергии основного состояния и аппроксимации волновой функции системы многих тел.

Можно сказать, что это вольный и упрощенный пересказ статьи [2], вышедшей в Science в 2017-м году и некоторых последующих работ. Я не нашел научно-популярных изложений этой работы на русском (да и из английских вариантов лишь этот), хотя она показалась мне очень интересной.

Минимальные необходимые понятия из квантовой механики и глубокого обучения

Сразу хочу отметить, что эти определения крайне упрощены. Я привожу их для тех, для кого описываемая проблематика — тёмный лес.

Состояние — это просто набор физических величин, которые описывают систему. Например, для летящего в пространстве электрона это будут его координаты и импульс, а для кристаллической решетки — набор спинов атомов, находящихся в её узлах.

Волновая функция системы — комплексная функция состояния системы. Некий чёрный ящик, который принимает на вход, например, набор спинов, а возвращает комплексное число. Основное важное для нас свойство волновой функции заключается в том, что её квадрат равен вероятности данного состояния:

$\Psi(s)\Psi(s)^* = P(s)$

Логично, что квадрат волновой функции должен быть нормирован на единицу (и это тоже одна из существенных проблем).

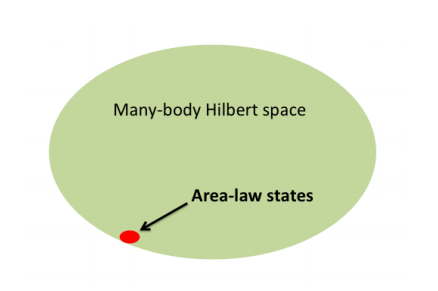
Гильбертово пространство — в нашем случае хватит такого определения — пространство всех возможных состояний системы. Например, для системы из 40 спинов, которые могут принимать значения +1 или -1, Гильбертово пространство — это все $2^{40}$ возможных состояний. Для координат, которые могут принимать значения $[-\infty, +\infty]$ , размерность Гильбертова пространства бесконечна. Именно огромная размерность Гильбертова пространства для любых реальных систем является основной проблемой, не позволяющей решать уравнения аналитически: в процессе будут возникать интегралы/суммирования по всему Гильбертову пространству, которые не вычисляются «в лоб». Любопытный факт: за всё время жизни Вселенной можно встретить лишь малую часть всех возможных состояний, входящих в Гильбертово пространство. Это очень хорошо иллюстрируется картинкой из статьи про Tensor Networks [1], на которой схематично изображено всё Гильбертово пространство и те состояния, которые можно встретить за полином от характеристики сложности пространства (числа тел, частиц, спинов и т.д.)

Ограниченная машина Больцмна — если объяснять сложно, то это неориентированная графическая вероятностная модель, ограниченность которой заключается в условной независимости вероятностей узлов одного слоя от узлов того же слоя. Если по-простому, то это нейронная сеть со входом и одним скрытым слоем. Значения выхода нейронов в скрытом слое могут быть равны 0 или 1. Отличие от обычной нейронной сети в том, что выходы нейронов скрытого слоя — это случайные величины, выбираемые с вероятностью, равной значению функции активации:

$P_i(1) = \sigma(b_i + \sum_jW_{ij}s_j)$

где $\sigma$ — сигмоидная функция активации, $inline$ — смещение для i-го нейрона, $inline$ — веса нейронной сети, $inline$ — видимый слой. Ограниченные машины Больцмана относятся к так называемым «энергетическим моделям», поскольку мы можем выразить вероятность того или иного состояния машины при помощи энергии этой машины:

$display$

где v и h — видимый и скрытый слои, a и b — смещения видимого и скрытого слоев, W — веса. Тогда вероятность состояния представима в виде:

$P(v, h) = \frac{1}{Z}e^{-E(v, h)}$

где Z — нормировочный член, называемый также статистической суммой (он необходим, чтобы полная вероятность равнялась единице).

Введение

Сегодня в среде специалистов по глубокому обучению существует мнение, что ограниченные
машины Больцмана (далее — ОМБ) это устаревшая концепция, которая практически неприменима в реальных задачах. Однако, в 2017 году в Science вышла статья [2], которая показала очень эффективное использование ОМБ для задач квантовой механики.

Авторы заметили два важных факта, которые могут показаться очевидными, но до того ни кому не приходили в голову:

ОМБ — это нейронная сеть, которая, согласно универсальной теореме Цыбенко, теоретически может аппроксимировать любую функцию со сколь угодно большой точностью (там еще много всяких ограничений, но их можно пропустить).
ОМБ — это система, вероятность каждого состояния которой есть функция от входа (видимого слоя), весов и смещений нейронной сети.

Ну и далее авторы сказали: а пусть наша система полностью описывается волновой функцией, которая есть корень из энергии ОМБ, а входы ОМБ — это характеристики нашего состояния системы (координаты, спины и т.д.):

$\Psi(s) = \frac{1}{Z}\sqrt{e^{E(s, h)}}$

где s — характеристики состояния (например, спины), h — выходы скрытого слоя ОМБ, E — энергия ОМБ, Z — нормировочная константа (статистическая сумма).

Всё, статья в Science готова, дальше остаётся лишь несколько маленьких деталей. Например, надо решить проблему невычислимой статистической суммы из-за гигантского размера Гильбертова пространства. А ещё теорема Цыбенко говорит нам, что нейронная сеть может аппроксимировать любую функцию, но совсем не говорит, как же нам найти подходящий для этого набор весов и смещений сети. Ну, и как водится, тут начинается самое интересное.

Обучение модели

Сейчас появилось довольно много модификаций первоначального подхода, но я буду рассматривать лишь подход из оригинальной статьи [2].

Задача

В нашем случае задача обучения будет следующей: найти такую аппроксимацию волновой функции, которая делала бы наиболее вероятным состояние с минимальной энергией. Интуитивно это понятно: волновая функция даёт нам вероятность состояния, собственное значение Гамильтониана (оператор энергии, или ещё проще, энергия — в рамках данной статьи такого понимания достаточно) для волновой функции есть энергия. Всё просто.

В реальности мы будем стремиться оптимизировать другую величину, так называемую локальную энергию, которая всегда больше или равна энергии основного состояния:

$E_{loc}(\sigma) = Re\sum_{\sigma\sigma'}H_{\sigma\sigma'}\frac{\Psi(\sigma')}{\Psi(\sigma)}$

здесь $\sigma$ — это наше состояние, $\sigma'$ — все возможные состояния Гильбертова пространства (в реальности мы будем считать более приближённое значение), $H_{\sigma\sigma'}$ — матричный элемент гамильтониана. Сильно зависит от конкретного гамильтониана, например, для модели Изинга это просто $f(\sigma)$ , если $\sigma = \sigma'$ , и $inline$ во всех остальных случаях. Не стоит сейчас на этом останавливаться; важно, что можно найти эти элементы для различных популярных гамильтонианов.

Процесс оптимизации

Сэмплирование

Важной частью подхода из оригинальной статьи был процесс сэмплирования. Использовалась модифицированная вариация алгоритма Метрополиса-Хастингса. Суть в следующем:

Начинаем из случайного состояния.
Меняем знак случайно выбранного спина на противоположный (для координат другие модификации, но они тоже есть).
С вероятностью, равной $P(\sigma'|\sigma) = \Big|{\frac{\Psi(\sigma')}{\Psi(\sigma)}}\Big|^2$ , переходим в новое состояние.
Повторить N раз.

В результате получаем набор случайных состояний, выбранных в соответствии с распределением, которое даёт нам наша волновая функция. Можно посчитать значения энергии в каждом состоянии и математическое ожидание энергии $\mathbb{E}(E_{loc})$ .

Можно показать, что оценка градиента энергии (точнее, ожидаемого значения гамильтониана) равна:

$G_k(x) = 2*(E_{loc}(x) - \mathbb{E}(E_{loc}))*D^*_k(x)$

Вывод

Это из лекций G. Carleo, которые он читал в 2017 году для Advanced School on Quantum Science and Quantum Technology. На Youtube есть записи.

Обозначим:

$D^*_k(x) = \frac{\partial_{p_k}\Psi(x)}{\Psi(x)}$

Тогда:

$\partial_{p_k}\mathbb{E}(H) =$

$\partial\frac{\sum_{xx'}\Psi^*(x)H_{xx'}\Psi(x')}{\sum_x|\Psi(x)|^2} =$

$\frac{\sum_{xx'}\Psi^*(x)H_{xx'}D_k(x')\Psi(x')}{\sum_x|\Psi(x)|^2} + \frac{\sum_{xx'}\Psi^*(x)D_k^*(x)H_{xx'}\Psi(x')}{\sum_x|\Psi(x)|^2} -$

$\frac{\sum_{xx'}\Psi^*(x)H_{xx'}\Psi(x')}{\sum_x|\Psi(x)|^2}\frac{\sum_x|\Psi(x)|^2(D_k(x) - D^*_k(x))}{\sum_x|\Psi(x)|^2} =$

$\frac{\sum_{xx'}\frac{\Psi^*(x)}{\Psi^*(x')}H_{xx'}D_k(x')|\Psi(x')|^2 + \sum_{xx'}|\Psi(x)|^2H_{xx'}D^*_k(x')\frac{\Psi(x')}{\Psi(x)}}{\sum_x|\Psi(x)|^2} -$

$\mathbb{E}(H)\frac{\sum_x|\Psi(x)|^2(D_k(x) + D^*_k(x))}{\sum_x|\Psi(x)|^2} \approx$

$\mathbb{E}(E_{loc}D^*_k) - \mathbb{E}(E_{loc})\mathbb{E}(D^*_k) + C$

Дальше просто решаем задачу оптимизации:

Сэмплируем состояния из нашей ОМБ.
Вычисляем энергию каждого состояния.
Оцениваем градиент.
Обновляем веса ОМБ.

В итоге градиент энергии стремится к нулю, значение энергии уменьшается, как и количество уникальных новых состояний в процессе Метрополиса-Хастингса, ведь сэмплируя из истинной волновой функции мы почти всегда будем получать основное состояние. Интуитивно это кажется логичным.

В оригинальной работе для небольших систем были получены значения энергии основного состояния, очень близкие к точным значениям, полученным аналитически. Было проведено сравнение с известными подходами нахождения энергии основного состояния, и NQS победил, особенно учитывая относительно низкую вычислительную сложность NQS в сравнении с известными методами.

NetKet — библиотека от «изобретателей» подхода

Один из авторов первоначальной статьи [2] со своей командой разработал прекрасную библиотеку NetKet [3], которая содержит очень хорошо оптимизированное (на мой взгляд) C-ядро, а также Python API, который работает с высокоуровневыми абстракциями.

Библиотеку можно установить через pip. Пользователям Windows 10 придётся воспользоваться Linux Subsystem for Windows.

Рассмотрим работу с библиотекой на примере цепочки из 40 спинов, принимающих значения +-1/2. Будем рассматривать модель Гейзенберга, в которой учитываются соседние взаимодействия.

У NetKet прекрасная документация, которая позволяет очень быстро разобраться, что и как делать. Есть как много встроенных моделей (спины, бозоны, модели Изинга, Гейзенберга и т.д.), так и возможность полностью описать модель самому.

Описание графа

Все модели представляются в виде графов. Для нашей цепочки подойдет встроенная модель Hypercube с одной размерностью и периодическими граничными условиями:

import netket as nk
graph = nk.graph.Hypercube(length=40, n_dim=1, pbc=True)

Описание Гильбертова пространства

Наше Гильбертово пространство очень простое — все спины могут принимать значения либо +1/2, либо -1/2. Для этого случая подойдет встроенная модель для спинов:

hilbert = nk.hilbert.Spin(graph=graph, s=0.5)

Описание Гамильтониана

Как я уже писал, в нашем случае гамильтониан — это гамильтониан Гейзенберга, для которого есть встроенный оператор:

hamiltonian = nk.operator.Heisenberg(hilbert=hilbert)

Описание RBM

В NetKet можно использовать готовую реализацию RBM для спинов — как раз наш случай. Но вообще машин там много, можно попробовать разные.

nk.machine.RbmSpin(hilbert=hilbert, alpha=4)
machine.init_random_parameters(seed=42, sigma=0.01)

Здесь альфа — это плотность нейронов скрытого слоя. Для 40 нейронов видимого и альфы 4 их будет 160. Есть другой способ указания, напрямую числом. Вторая команда инициализирует веса случайным образом из $N(0, \sigma)$ . В нашем случае сигма равна 0.01.

Сэмлер

Сэмплер — это объект, который нам будет возвращать выборку из нашего распределения, которое задается на Гильбертовом пространстве волновой функцией. Будем использовать описанный выше алгоритм Метрополиса-Хастингса, модифицированный под нашу задачу:

sampler = nk.sampler.MetropolisExchangePt(
  machine=machine,
  graph=graph,
  d_max=1,
  n_replicas=12
)

Если быть совсем точным, сэмплер более хитрый алгоритм, чем тот, который я описывал выше. Тут мы одновременно проверяем целых 12 вариантов параллельно, чтобы выбрать следующую точку. Но принцип, в целом, тот же.

Оптимизатор

Здесь описывается оптимизатор, который будет использоваться для обновления весов модели. По личному опыту работы с нейронными сетями в более «привычных» для них областях, самый лучший и надежный вариант — старый добрый стохастический градиентный спуск с моментом (хорошо описан тут):

opt = nk.optimizer.Momentum(learning_rate=1e-2, beta=0.9)

Обучение

В NetKet есть обучение как без учителя (наш случай), так и с учителем (например, так называемая «квантовая томография», но это тема отдельной статьи). Просто описываем «учителя», и всё:

vc = nk.variational.Vmc(
  hamiltonian=hamiltonian,
  sampler=sampler,
  optimizer=opt,
  n_samples=1000,
  use_iterative=True
)

Вариационный Монте-Карло указывает на то, каким образом мы оцениваем градиент функции, которую оптимизируем. n_smaples — это размер выборки из нашего распределения, которую возвращает сэмплер.

Результаты

Запускать модель будем следующим образом:

vc.run(output_prefix=output, n_iter=1000, save_params_every=10)

Библиотека построена с использованием OpenMPI, и скрипт необходимо будет запускать примерно так: mpirun -n 12 python Main.py (12 — количество ядер).

Результаты я получил следующие:

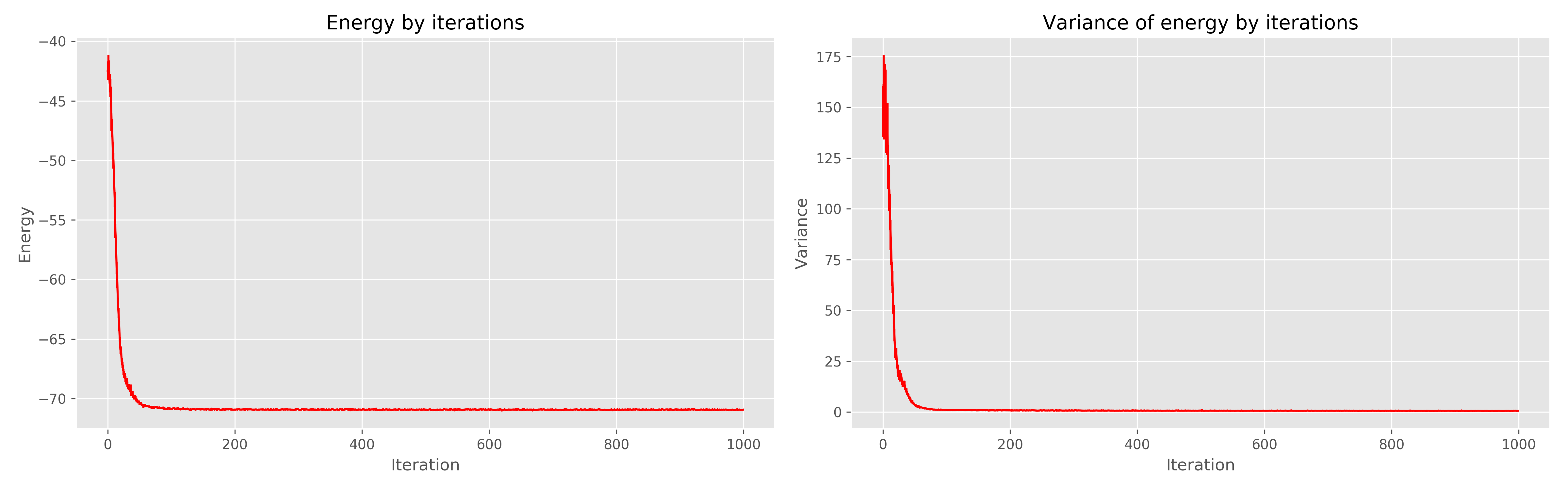
Слева график энергии от эпохи обучения, справа — дисперсии энергии от эпохи обучения.
Видно, что 1000 эпох явно избыточно, хватило бы и 300. В целом работает очень круто, сходится быстро.

Литература

Orús R. A practical introduction to tensor networks: Matrix product states and projected entangled pair states //Annals of Physics. – 2014. – Т. 349. – С. 117-158.
Carleo G., Troyer M. Solving the quantum many-body problem with artificial neural networks //Science. – 2017. – Т. 355. – №. 6325. – С. 602-606.
www.netket.org

Tags:

Hubs: