
После настоящего бума настольных игр конца 00-х в семье осталась несколько коробок с играми. Одна из них — игра “Заяц и Ёж” в оригинальной немецкой версии. Игра для нескольких игроков, в которой элемент случайности сведен к минимуму, а побеждает трезвый расчет и способность играющего “заглядывать” вперед на несколько шагов.
Мои частые поражения в игре привели меня к мысли написать компьютерный “интеллект” для выбора наилучшего хода. Интеллект, в идеале, способный сразиться с гроссмейстером Зайца и Ежа (а что, чай, не шахматы, игра попроще будет). Далее в статье идет описание процесса разработки, логики AI и ссылка на исходники.
Правила игры Заяц и Ёж
На игровом поле в 65 клеток размещены несколько фишек игроков, от 2 до 6 участников (рисовка моя, неканоничная, выглядит, конечно, так себе):
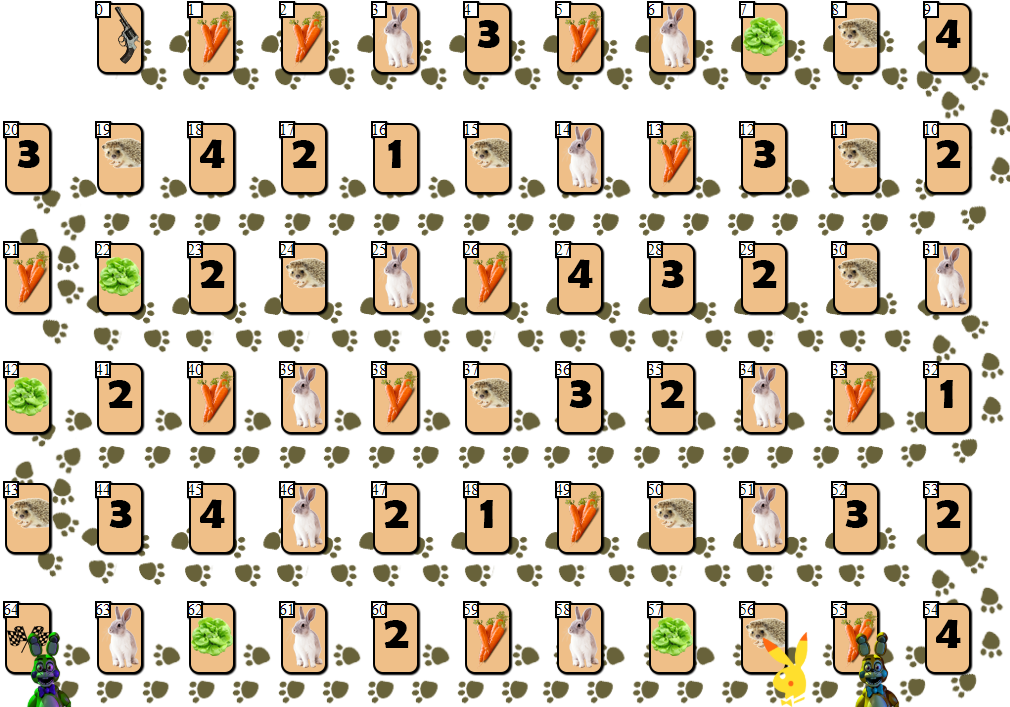
Не считая клеток с индексами 0 (старт) и 64 (финиш), в каждой из клеток может размещаться только один игрок. Цель каждого из игроков — продвинуться вперед на финишную клетку, опередив соперников.
“Топливом” для продвижения вперед является морковка — игровая “валюта”. На старте каждый игрок получает 68 морковок, которые отдает (а иногда и получает) по мере продвижения.
Кроме морковок, на старте игрок получает 3 карточки салата. Салат — особый “артефакт”, от которого игрок должен избавиться до финиша. Избавляясь от салата (а сделать это можно только на специальной клетке салата, вот такой:

), игрок, в том числе, получает дополнительные морковки. Перед этим пропустив свой ход. Чем больше игроков впереди уходящего с карты салата, тем больше морковок получит тот игрок: 10 х (позиция игрока на поле относительно других игроков). То есть, игрок, стоящий на поле вторым, получит 20 морковок, покидая клетку салата.
Клетки с цифрами 1 — 4 могут принести несколько десятков морковок, если позиция игрока совпадает с номером на клетке (1 — 4, клетка с номером 1 также подходит для 4 и 6-й позиций на поле), по аналогии с клеткой салата.
Игрок может пропустить ход, оставшись на клетке с изображением моркови и получить либо отдать за это действие 10 морковок. Зачем игроку отдавать “топливо”? Дело в том, что финишировать игрок может лишь имея после своего завершающего хода 10 морковок (20 если финишируешь вторым, 30 если третьим и т.д.).
Наконец, игрок может получить 10 x N морковок, сделав N шагов на ближайшего свободного ежа (если ближайший еж занят, такой ход невозможен).
Стоимость продвижения вперед рассчитывается не пропорционально количеству ходов, по формуле (с округлением вверх):
где N — количество шагов вперед.
Так для шага вперед на одну клетку игрок отдает 1 морковку, 3 морковки за 2 клетки, 6 морковок за 3 клетки, 10 за 4, …, 210 морковок за перемещение на 20 клеток вперед.
Последняя клетка — клетка с изображением зайца — вносит в игру элемент случайности. Встав на клетку с зайцем игрок тянет из стопки специальную карточку, после которой производится некоторое действие. В зависимости от карточки и игровой ситуации, игрок может потерять часть морковок, получить дополнительные морковки или пропустить один ход. Стоит отметить, что среди карточек с “эффектами” несколько больше негативных для игрока сценариев, что поощряет игру осторожную и просчитанную.
Реализация без AI
В самой первой реализации, что станет потом основой для разработки игрового “интеллекта”, я ограничился вариантом, в котором каждый ход делает игрок — человек.
Игру я решил реализовать как клиент — статический одностраничный вебсайт, вся “логика” которого реализована на JS и сервер — WEB API приложение. Сервер написан на .NET Core 2.1 и дает на выходе один артефакт сборки — файл dll, который может выполняться под Windows / Linux / Mac OS.
“Логика” клиентской части сведена к минимуму (так же, как и UX, так как GUI чисто утилитарный). Например, web-клиент не выполняет сам проверку — допустим ли правилами ход, запрошенный игроком. Эта проверка выполняется на сервере. Сервер же подсказывает клиенту, какие ходы игрок может сделать из текущей игровой позиции.
Сервер представляет собой классический автомат Мура. В серверной логике отсутствуют такие понятия, как “подключенный клиент”, “игровая сессия” и т.д.
Все, что делает сервер — обрабатывает полученную (HTTP POST) команду. На сервере реализован паттерн “команда”. Клиент может запросить выполнение одной из следующих команд:
- начать новую игру, т.е. “расставить” фишки указанного количества игроков на “чистой” доске
- сделать ход, указанный в команде
Для второй команды клиент отправляет серверу текущую игровую позицию (объект класса Disposition), т.е., описание следующего вида:
- позиция, количество морковки и салата для каждого зайца плюс дополнительное булево поле, указывающее на то, что заяц пропускает свой ход
- индекс зайца, совершающего ход.
Серверу не нужно отправлять дополнительную информацию — например, информацию о игровом поле. Так же, как для записи шахматного этюда необязательно расписывать расстановку черных и белых клеток на доске — эта информация принята за константу.
В ответе сервер указывает, успешно ли выполнена команда. Технически, клиент может, к примеру, запросить недопустимый ход. Или попытаться создать новую игру для единственного участника, что, очевидно, не имеет смысла.
Если команда выполнена успешно, в ответе будет содержаться новая игровая позиция, а также перечень ходов, которые может сделать следующий в очереди (текущий для новой позиции) игрок.
Дополнительно к этому, ответ сервера содержит некоторые служебные поля. Например, текст карточки зайца, “вытащенной” игроком при шаге на соответствующую клетку.
Ход игрока
Ход игрока кодируется целым числом:
- 0, если игрок вынужден остаться на текущей клетке,
1, 2, … N для 1, … N шагов вперед, - -1, -2, … -M для перемещения на 1 … M клеток назад на ближайшего свободного ежа,
- 1001, 1002 — специальные коды для игрока, решившего остаться на клетке моркови и получить (1001) или отдать (1002) за это 10 морковок.
Программная реализация
Сервер получает JSON запрошенной команды, парсит его в один из соответствующих классов запроса, и выполняет затребованное действие.
Если клиент (игрок) запросил произвести ход с кодом CMD из переданной в команде позиции (POS), сервер производит следующие действия:
- проверяет, возможен ли такой ход
- создает новую позицию из текущей, применяя к ней соответствующие модификации,
получает множество возможных ходов для новой позиции. Напомню, индекс игрока, совершающего ход, уже включен в объект, описывающий позицию, - возвращает клиенту ответ с новой позицией, возможными ходами либо флагом success, равным false, и описанием ошибки.
Логика проверки допустимости запрошенного хода (CMD) и построения новой позиции оказались связанными чуть теснее, чем хотелось бы. С этой логикой перекликается и метод поиска допустимых ходов. Весь этот функционал реализует класс TurnChecker.
На входе методов проверки / выполнения хода TurnChecker получает объект класса игровой позиции (Disposition). Объект Disposition содержит массив с данными игроков (Haze[] hazes), индекс игрока, совершающего ход + некоторую служебную информацию, заполняемую в процессе работы объекта TurnChecker.
Игровое поле описывает класс FieldMap, который реализован, как синглтон. Класс содержит массив клеток + некоторую служебную информацию, используемую для упрощения / ускорения последующих расчетов.
Соображения производительности
В реализации класса TurnChecker я старался, насколько возможно, избегать циклов. Дело в том, что методы получения множества допустимых ходов / выполнения хода впоследствии будут вызываться тысячи (десятки тысяч) раз в ходе процедуры поиска квазиоптимального хода.
Так, к примеру, я вычисляю, сколько клеток игрок может пройти вперед, располагая N морковками, по формуле:
Проверяя, не занята ли клетка i одним из игроков, я не пробегаю по списку игроков (так как это действие придется, вероятно, выполнять многократно), а обращаюсь к словарю вида [индекс_клетки, флаг_занятой_клетки], заполненному заранее.
При проверке, является ли указанная клетка ежа ближайшей (позади) по отношению к текущей клетке, занимаемой игроком, я также сравниваю запрошенную позицию со значением из словаря вида [индекс_клетки, индекс_ближайшего_сзади_ежа] — статической информацией.
Так, к примеру, я вычисляю, сколько клеток игрок может пройти вперед, располагая N морковками, по формуле:
return ((int)Math.Pow(8 * N + 1, 0.5) - 1) / 2;
Проверяя, не занята ли клетка i одним из игроков, я не пробегаю по списку игроков (так как это действие придется, вероятно, выполнять многократно), а обращаюсь к словарю вида [индекс_клетки, флаг_занятой_клетки], заполненному заранее.
При проверке, является ли указанная клетка ежа ближайшей (позади) по отношению к текущей клетке, занимаемой игроком, я также сравниваю запрошенную позицию со значением из словаря вида [индекс_клетки, индекс_ближайшего_сзади_ежа] — статической информацией.
Реализация с AI
В список команд, обрабатываемых сервером, добавляется одна команда: выполнить квазиоптимальный, выбранный программой, ход. Эта команда — небольшая модификация команды “ход игрока”, из которой убрано, собственно, поле хода (CMD).
Первое решение, которое приходит в голову — использовать эвристику для выбора “наилучшего из возможных” хода. По аналогии с шахматами, мы можем оценить каждую из игровых позиций, получаемую с нашим ходом, выставив этой позиции какую-то оценку.
Эвристическая оценка позиции
К примеру, в шахматах, произвести оценку (не залезая в дебри дебютов) довольно просто: как минимум, можно посчитать суммарную “стоимость” фигур, приняв стоимость коня / слона за 3 пешки, стоимость ладьи 5 пешек, ферзя — 9, короля — int.MaxValue пешек. Оценку несложно улучшить, например, добавив к ней (с поправочным коэффициентом — сомножителем / показателем степени или иной функцией):
- количество возможных ходов из текущей позиции,
- соотношение угроз фигурам противника / угроз от противника.
Особая оценка выставляется позиции мата: int.MaxValue, если мат поставил компьютер, int.MinValue если мат поставил человек.
Если приказать шахматному процессору выбирать следующий ход, руководствуясь лишь такой оценкой, процессор выберет, вероятно, не самые худшие ходы. В частности:
- не упустит возможность взять фигуру покрупней или поставить мат,
- скорее всего, не загонит фигуры по углам,
- не подставит лишний раз фигуру под удар (если учесть в оценке количество угроз).
Конечно, такие ходы компьютера не оставят ему шанса на успех с противником, совершающим свои ходы мало-мальски осмысленно. Компьютер проигнорирует любую из вилок. Вдобавок, не постесняется даже, вероятно, разменять ферзя на пешку.
Тем не менее, алгоритм эвристической оценки текущей игровой позиции в шахматах (не претендуя на лавры программы-чемпиона) довольно прозрачен. Чего не скажешь об игре Заяц и Ёж.
В общем случае, в игре Заяц и Ёж, работает довольно размытая максима: “лучше зайти подальше, имея морковок побольше, а салата поменьше”. Однако не всё так прямолинейно. Скажем, если игрок имеет на руках 1 карту салата в середине игры, этот вариант может быть вполне неплох. А вот игрок, стоящий у финиша с картой салата, очевидно, окажется в проигрышной ситуации. Вдобавок от алгоритма оценки хотелось бы также получить возможность “подглядеть” на шаг вперед, подобно тому, как в эвристической оценке шахматной позиции можно посчитать угрозы фигурам. Например, стоит учесть бонус морковок, получаемых игроком, уходящим с клетки салата / клетки позиции (1… 4), с учетом количества игроков впереди.
Итоговую оценку я вывел в виде функции:
E = Ks * S + Kc * C + Kp * P,
где S, C, P — оценки, посчитанные по карточкам салата (S) и морковки © на руках у игрока, P — оценка, данная игроку за пройденное расстояние.
Ks, Kc, Kp — соответствующие поправочные коэффициенты (о них речь пойдет позже).
Проще всего я определил оценку за пройденный путь:
P = i * 3, где i — индекс клетки, на которой находится игрок.
Оценка C (морковок) производится уже сложней.
Для получения конкретного значения C, я выбираю одну из 3-х функций
- [0], если игрок прошел менее половины игрового поля,
- [2], если у игрока достаточно (м.б., даже с избытком) морковки, чтобы финишировать,
- [1] в остальных случаях.
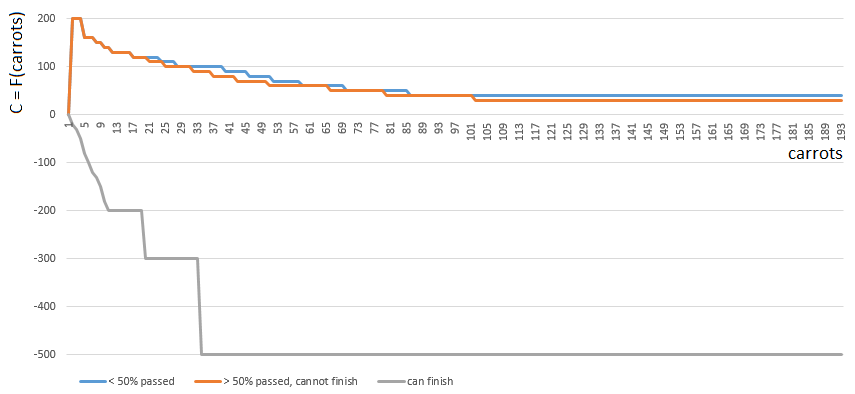
Функции 0 и 1 похожи: “ценность” каждой морковки на руках игрока плавно снижается с ростом количества морковки на руках. Игра редко поощряет “Плюшкиных”. В случае 1 (половина поля пройдена) ценность морковки снижается чуть быстрей.
Функция 2 (игрок может финишировать), наоборот, накладывает большой штраф (отрицательное значение коэффициента) на каждую морковку на руках игрока — чем больше морковки, тем больше штрафной коэффициент. Так как с избытком морковки финиш запрещен правилами игры.
Перед расчетом количество морковки на руках игрока уточняется с учетом морковок за ход с клетки салата / клетки с номером 1… 4.
“Салатная” оценка S выводится похожим образом. В зависимости от количества салата на руках игрока (0…3) выбирается функция
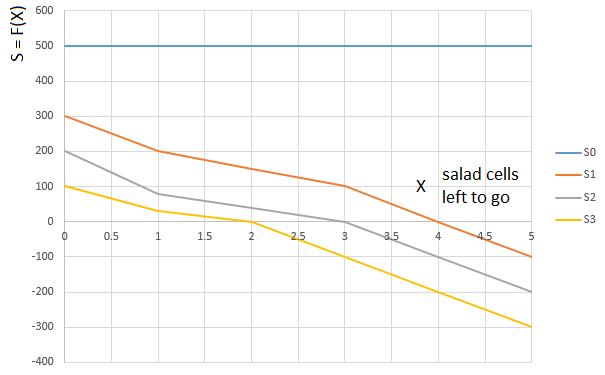
Кривая
кривая
Итоговая оценка (E = Ks * S + Kc * C + Kp * P), таким образом, учитывает:
- дополнительное количество морковки, которое игрок получит непосредственно перед собственным ходом,
- пройденный игроком путь,
- количество морковки и салата на руках, нелинейно влияющих на оценку.
А вот как играет компьютер, выбирающий следующий ход по максимуму эвристической оценки:
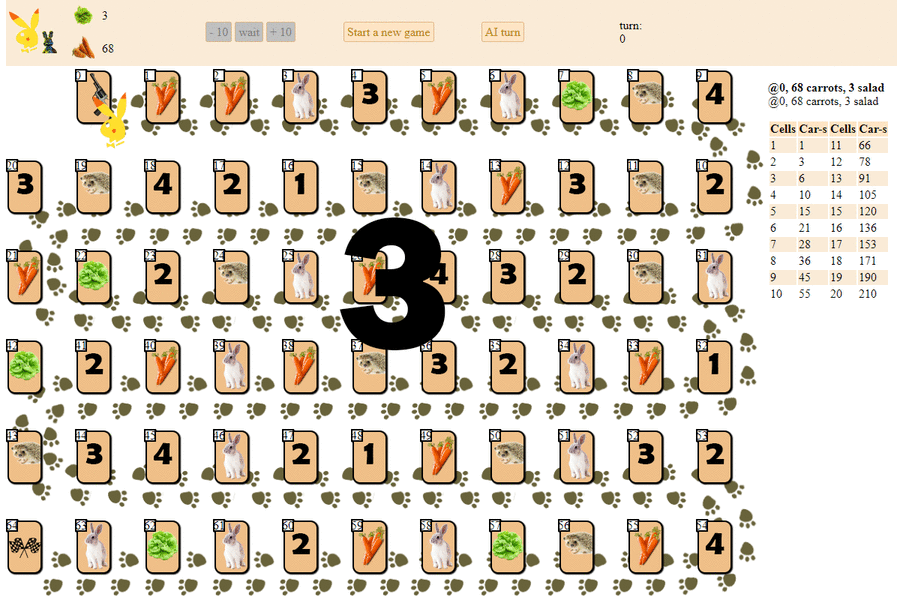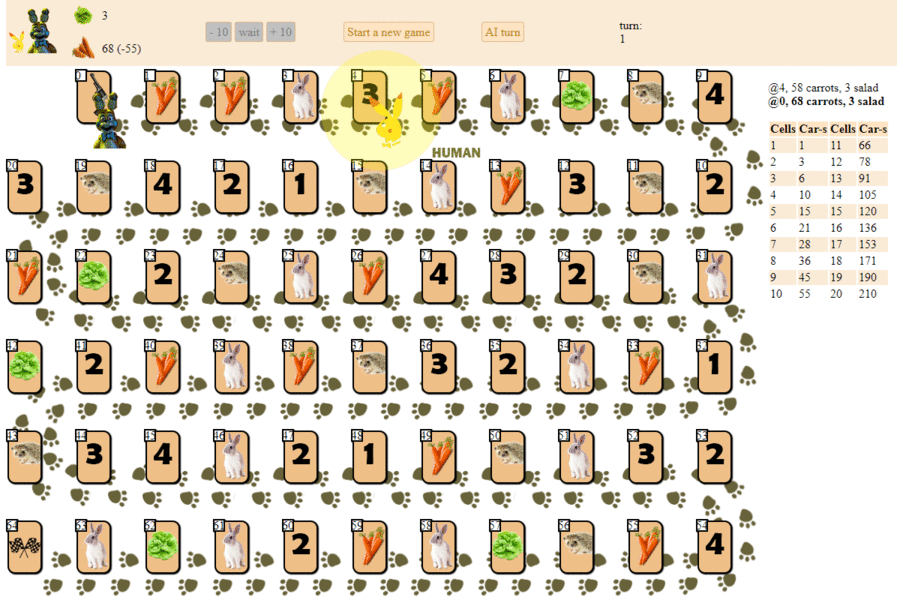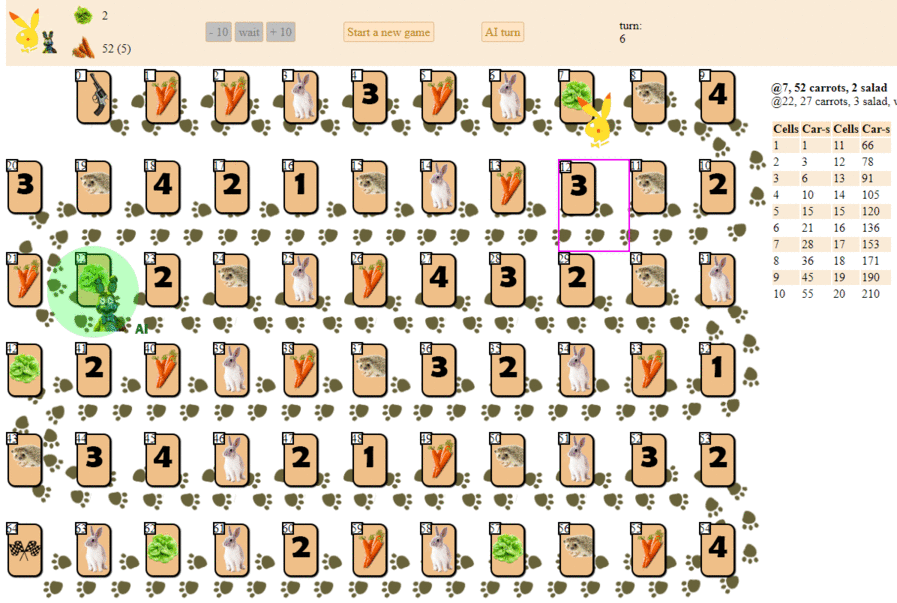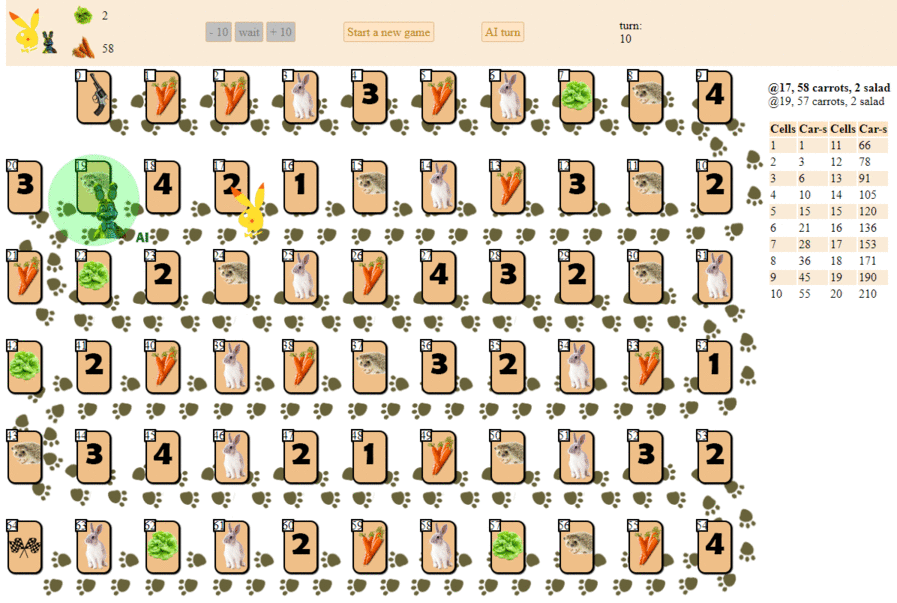
В принципе, дебют не так плох. Однако и хорошей игры от такого AI ожидать не стоит: к середине партии зеленый “робот” начинает делать повторяющиеся ходы, а к концу совершает несколько итераций ходов вперед — назад на ежа, пока, наконец, не финиширует. Финиширует, отчасти, благодаря случайности, отстав от игрока — человека на десяток ходов.
Замечания по реализации
Расчетом оценки заведует особый класс — EstimationCalculator. Функции оценки позиции относительно карточек моркови — салата загружаются в массивы в статическом конструкторе класса-калькулятора. На вход метод оценки позиции получает собственно объект позиции и индекс игрока, с “точки зрения” которого позиция оценивается алгоритмом. Т.е., одна и та же игровая позиция может получить несколько разных оценок, в зависимости от того, для какого игрока считаются виртуальные очки.
Дерево решений и алгоритм Минимакс
Используем алгоритм принятия решения в антагонистической игре “Минимакс”. Очень неплохо, на мой взгляд, алгоритм описан в этом посте (перевод).
Научим программу “заглядывать” на несколько ходов вперед. Предположим, из текущей позиции (а алгоритму не важна предыстория — как мы помним, программа функционирует как автомат Мура), пронумерованной цифрой 1, программа может сделать два хода. Получим две возможных позиции, 2 и 3. Далее наступает черед игрока — человека (в общем случае — противника). Из 2-й позиции противнику доступны 3 хода, из третьей — только два хода. Далее очередь сделать ход снова выпадает программе, которая, в общей сложности, может сделать 10 ходов из 5 возможных позиций:
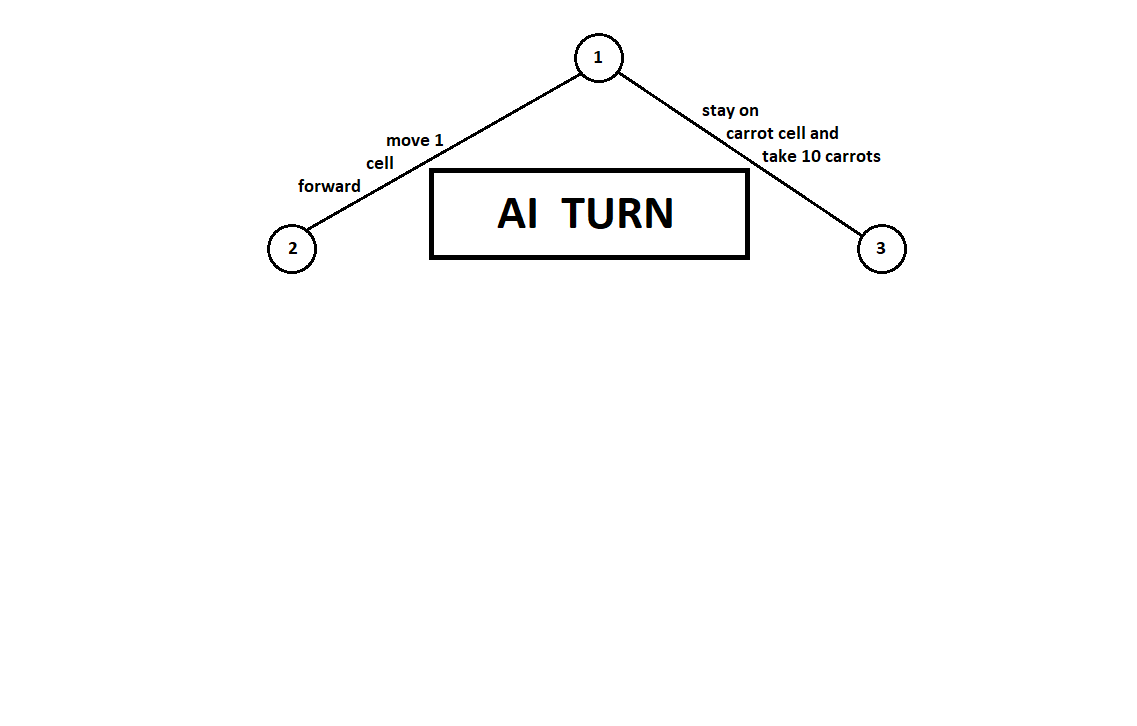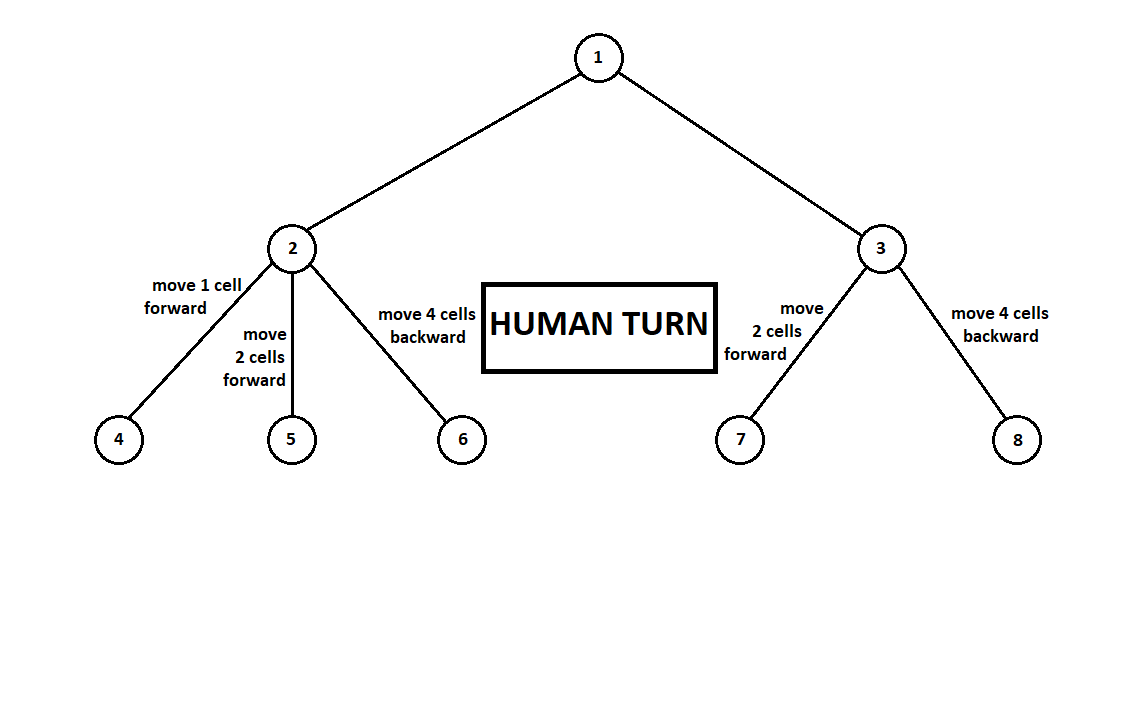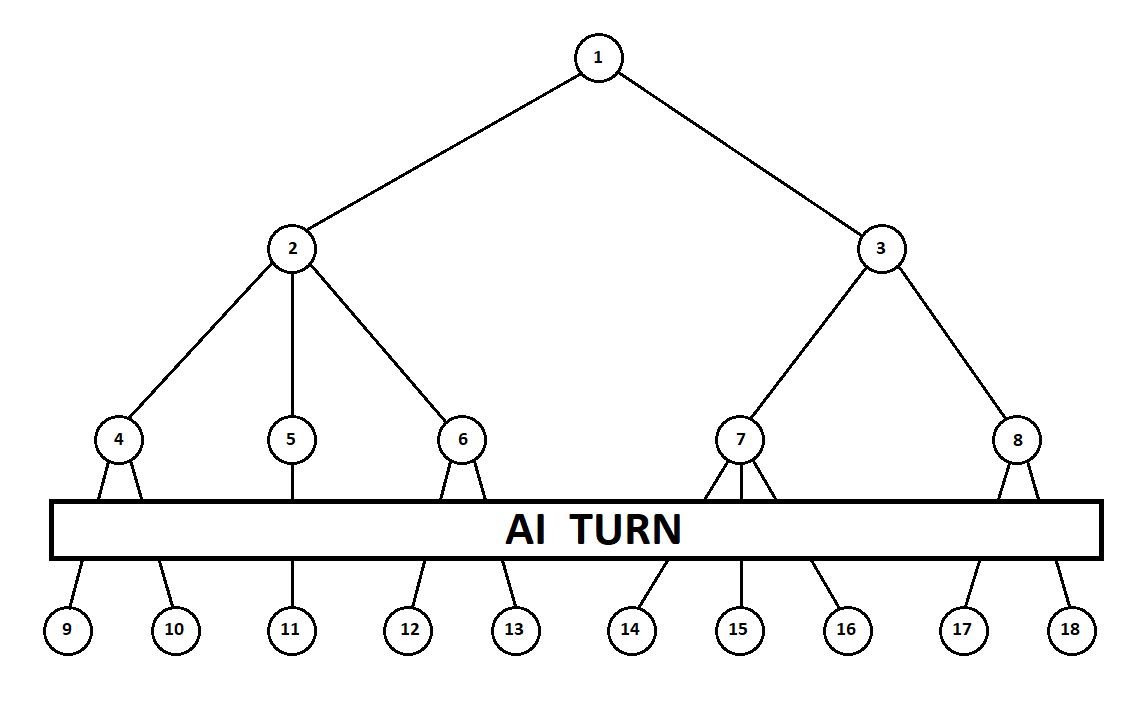
Предположим, после второго хода компьютера игра завершается и каждая из полученных позиций оценивается с точки зрения первого и второго игроков. А алгоритм оценки у нас уже реализован. Оценим каждую из финальных позиций (листьев дерева 9… 18) в виде вектора
где
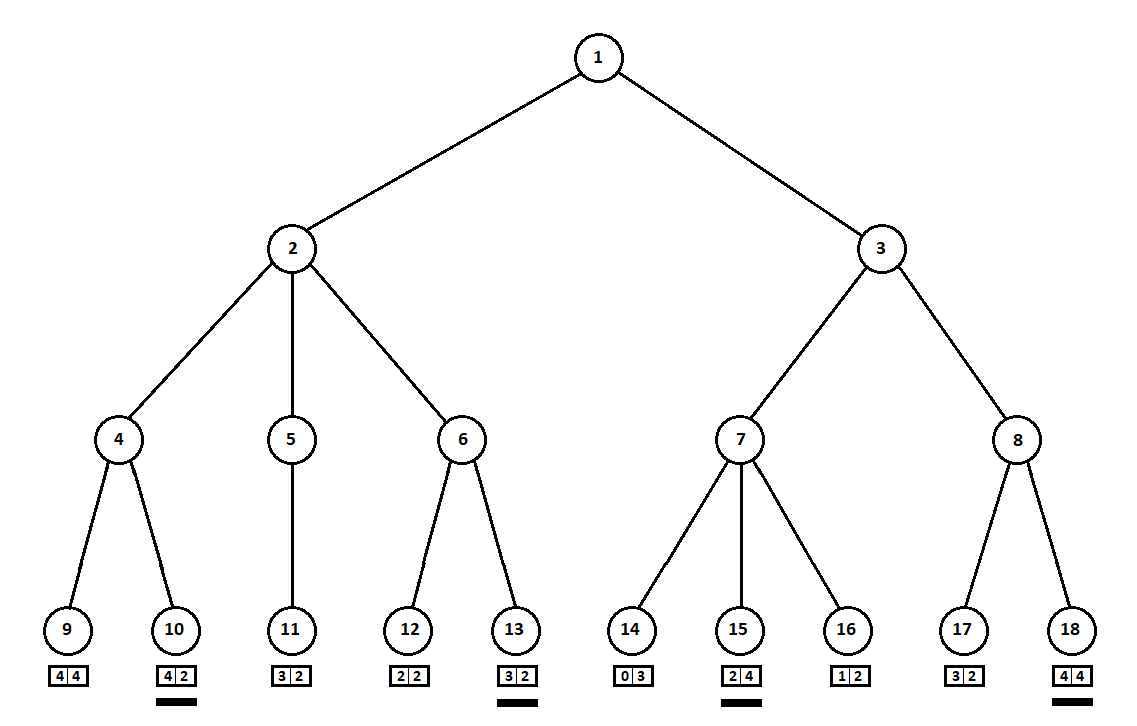
Так как последний ход делает компьютер, он, очевидно, выберет в каждом из поддеревьев вариантов ([9, 10], [11], [12, 13], [14, 15, 16], [17, 18]) тот, что дает ему лучшую оценку. Сразу возникает вопрос: по какому принципу выбирать “лучшую” позицию?
Например, есть два хода, после которых имеем позиции с оценками [5; 5] и [2; 1]. Оценивает первый игрок. Очевидны две альтернативы:
- выбор позиции с максимальным абсолютным значением i-ой оценки для i-го игрока. Иначе говоря, благородный гонщик Лесли, рвущийся к победе, без оглядки на конкурентов. В таком случае будет выбрана позиция с оценкой [5; 5].
- выбор позиции с максимальной оценкой относительно оценок конкурентов — хитроумный профессор Фейт, не упускающий возможности учинить противнику пакость. Например, намеренно отстать от игрока, планирующего стартовать со второй позиции. Будет выбрана позиция с оценкой [2; 1].
В своей программной реализации я сделал алгоритм выбора оценки (функцию, отображающую вектор оценки на скалярную величину для i-го игрока) настраиваемым параметром. Дальнейшие тесты показали, к некоторому моему удивлению, превосходство первой стратегии — выбор позиции по максимальному абсолютному значению
Особенности программной реализации
Если в настройках AI (класса TurnMaker) указан первый вариант выбора лучшей оценки, код соответствующего метода примет вид:
Второй метод — максимум относительно позиций конкурентов — реализован чуть сложней:
int ContractEstimateByAbsMax(int[] estimationVector, int playerIndex)
{
return estimationVector[playerIndex];
}
Второй метод — максимум относительно позиций конкурентов — реализован чуть сложней:
int ContractEstimateByRelativeNumber(int[]eVector, int player)
{
int? min = null;
var pVal = eVector[player];
for (var i = 0; i < eVector.Length; i++)
{
if (i == player) continue;
var val = pVal - eVector[i];
if (!min.HasValue || min.Value > val)
min = val;
}
return min.Value;
}
Выбранные оценки (подчеркнуты на рисунке) переносим на уровень вверх. Теперь противнику предстоит выбрать позицию, зная, какую последующую позицию выберет алгоритм:
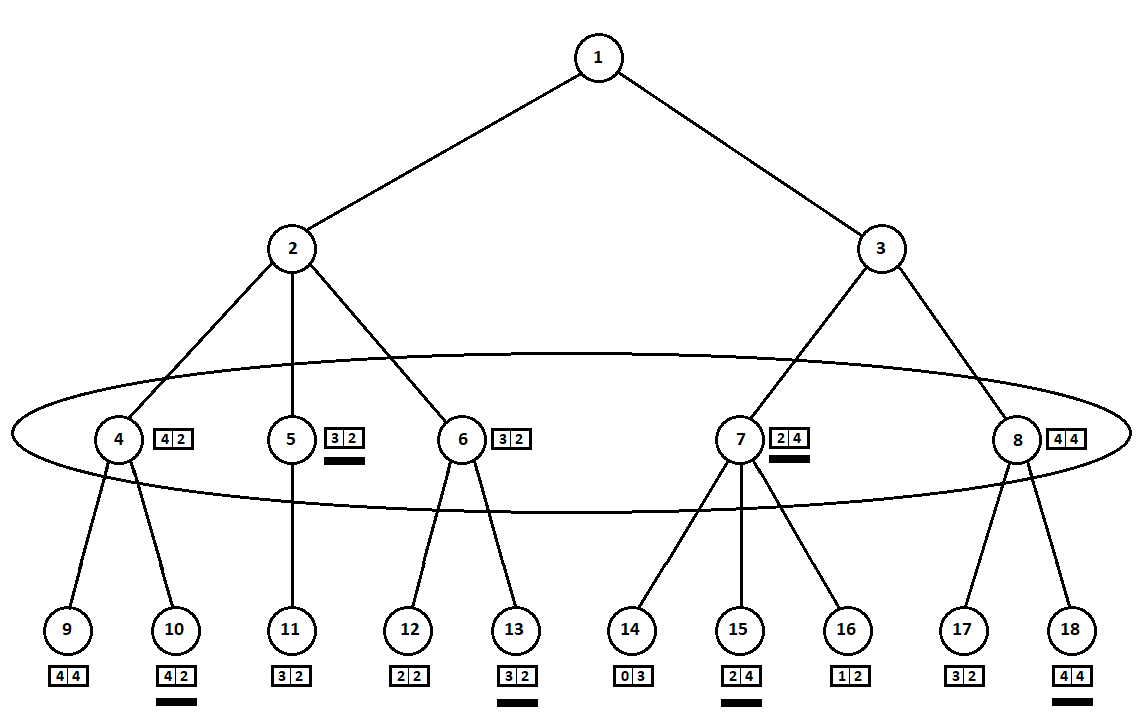
Противник, очевидно, выберет позицию с лучшей для себя оценкой (той, где вторая координата вектора принимает наибольшее значение). Эти оценки снова подчеркнуты на графике.
Наконец, возвращаемся на самый первый ход. Выбирает компьютер, и он отдает предпочтение ходу с наибольшей первой координатой вектора:
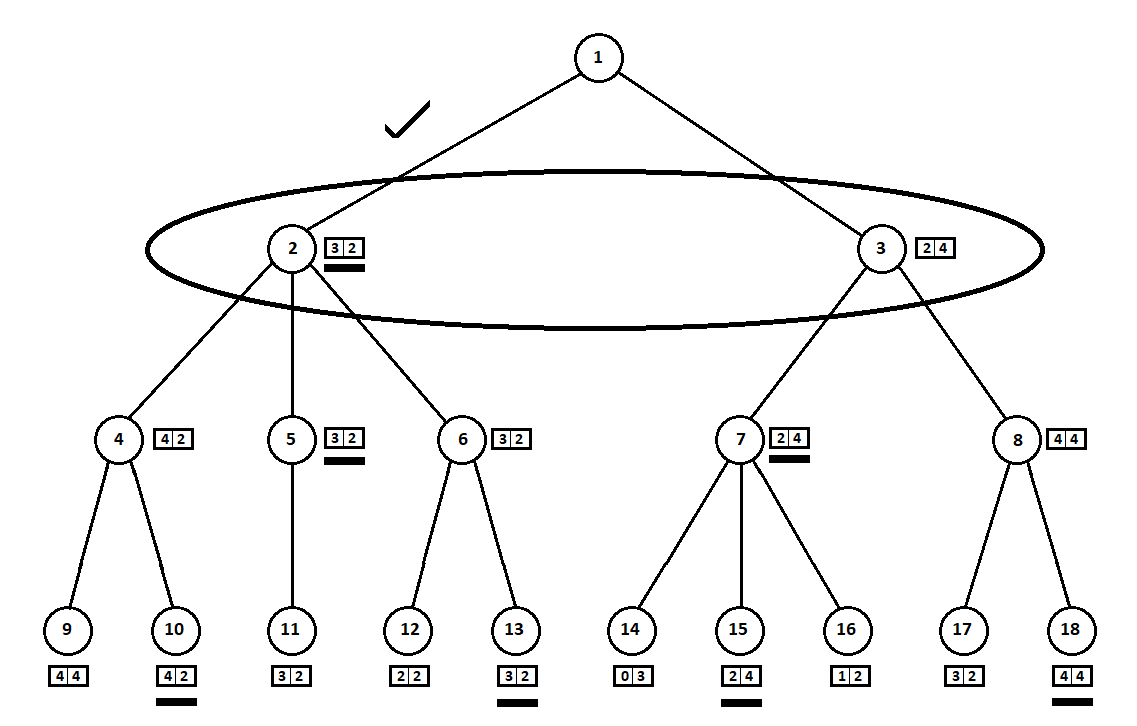
Таким образом, задача решена — найден квазиоптимальный ход. Предположим, эвристическая оценка в позициях-листьях дерева на 100% указывает на будущего победителя. Тогда наш алгоритм однозначно выберет лучший из возможных ходов.
Однако эвристическая оценка точна на 100% лишь тогда, когда оценивается финальная позиция игры — один (или несколько) игроков финишировали, победитель определился. Следовательно, имея возможность заглянуть на N ходов вперед — на столько, сколько потребуется для победы равных по “силе” соперников, можно выбрать оптимальный ход.
Но типовая партия для 2-х игроков длится в среднем около 30 — 40 ходов (для трех игроков — около 60 ходов и т.д.). Из каждой позиции игрок может сделать, как правило, около 8 ходов. Следовательно, полное дерево возможных позиций для 30 ходов будет состоять из примерно
На практике, построение и “разбор” дерева из ~ 100 000 позиций на моем ПК занимает порядка 300 миллисекунд. Что дает нам ограничение на глубину дерева в 7 — 8 уровней (ходов), если мы хотим ожидать ответа компьютера не более секунды.
Особенности программной реализации
Для построения дерева позиций и отыскания лучшего хода, очевидно, потребуется рекурсивный метод. На входе метода — текущая позиция (в которой, как мы помним, уже указан игрок, совершающий ход) и текущий уровень дерева (номер хода). Как только мы опускаемся на максимальный допустимый настройками алгоритма уровень, функция возвращает вектор эвристической оценки позиции с “точки зрения” каждого из игроков.
Важное дополнение: спуск ниже по дереву необходимо прекратить также в том случае, когда текущий игрок финишировал. Иначе (если выбран алгоритм отбора лучшей позиции относительно позиций других игроков) программа может довольно долго “топтаться” у финиша, “глумясь” над соперником. К тому же, так мы немного уменьшим размеры дерева в эндшпиле.
Если мы еще не находимся на предельном уровне рекурсии, то выбираем возможные ходы, создаем новую позицию для каждого хода и передаем ее в рекурсивный вызов текущего метода.
Важное дополнение: спуск ниже по дереву необходимо прекратить также в том случае, когда текущий игрок финишировал. Иначе (если выбран алгоритм отбора лучшей позиции относительно позиций других игроков) программа может довольно долго “топтаться” у финиша, “глумясь” над соперником. К тому же, так мы немного уменьшим размеры дерева в эндшпиле.
Если мы еще не находимся на предельном уровне рекурсии, то выбираем возможные ходы, создаем новую позицию для каждого хода и передаем ее в рекурсивный вызов текущего метода.
Почему “Минимакс”?
В оригинальной трактовке игроков всегда двое. Программа рассчитывает оценку исключительно с позиции первого игрока. Соответственно, при выборе “лучшей” позиции, игрок с индексом 0 ищет позицию с максимумом оценки, игрок с индексом 1 — с минимумом.
В нашем случае оценка должна быть вектором, чтобы каждый из N игроков мог оценить ее со своей “точки зрения”, по мере того как оценка поднимается вверх по дереву.
В нашем случае оценка должна быть вектором, чтобы каждый из N игроков мог оценить ее со своей “точки зрения”, по мере того как оценка поднимается вверх по дереву.
Тюнинг AI
Моя практика игры против компьютера показала, что алгоритм не так плох, но все же пока уступает человеку. Улучшать AI я решил в двух направлениях:
- оптимизировать построение / прохождение дерева решений,
- улучшить эвристику.
Оптимизация алгоритма Минимакс
В примере выше мы могли бы отказаться от рассмотрения позиции 8 и “сэкономить” 2 — 3 вершины дерева:
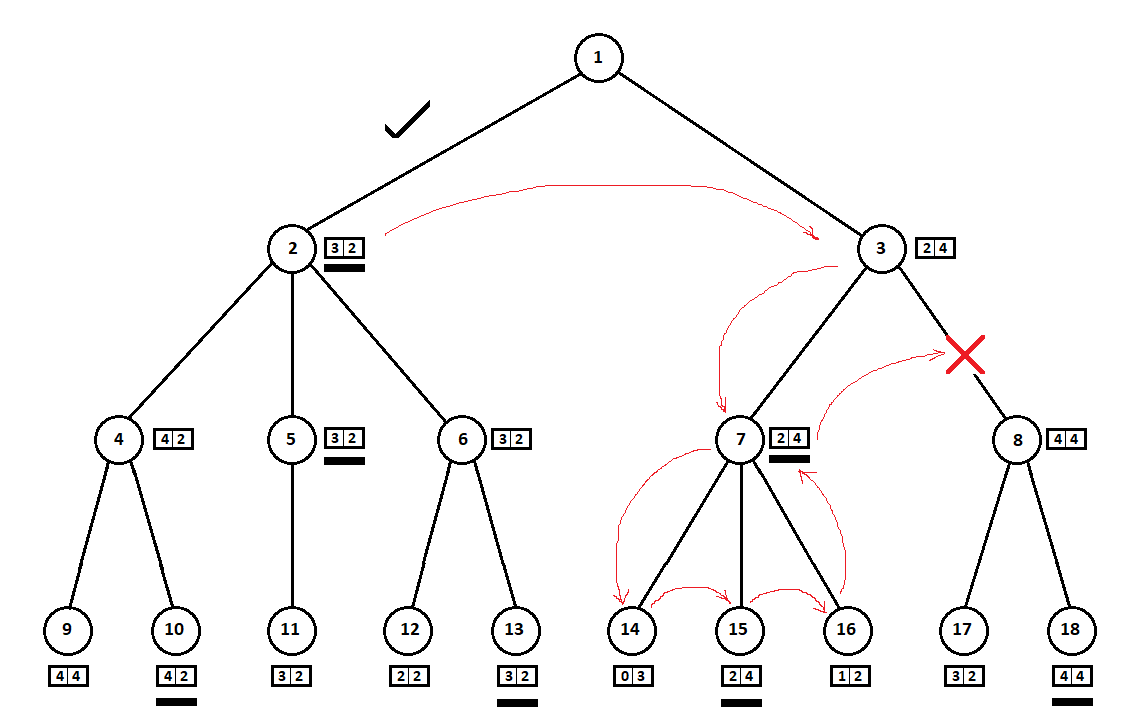
Обход дерева производим сверху-вниз, слева-направо. Обойдя поддерево, начинающееся с позиции 2, мы вывели лучшую для хода 1 -> 2 оценку: [3, 2]. Обойдя поддерево с корнем в позиции 7, мы определили текущую (лучшую для хода 3 -> 7) оценку: [2, 4]. С точки зрения компьютера (первого игрока) оценка [2, 4] хуже оценки [3, 2]. А так как противник компьютера выбирает ход из позиции 3, какой бы ни была оценка для позиции 8, итоговая оценка для позиции 3 будет априори хуже оценки, полученной для третьей позиции. Соответственно, поддерево с корнем в позиции 8 можно не строить и не оценивать.
Оптимизированная версия Минимакс алгоритма, позволяющая отсечь лишние поддеревья, называется алгоритмом альфа-бета отсечения. Для реализации этого алгоритма потребуются незначительные модификации исходного кода.
Особенности программной реализации
в метод CalcEstimate класса TurnMaker дополнительно передаются два целочисленных параметра — alpha, равный изначально int.MinValue и beta, равный int.MaxValue. Далее, после получения оценки текущего рассматриваемого хода, выполняется псевдокод вида:
e = вектор_оценок[0] // оценка текущей позиции для первого игрока
если (ход первого игрока)
если (e > alpha)
alpha = e
иначе
если (e < beta)
beta = e
если (beta <= alpha)
завершить перебор возможных ходов
Важная особенность программной реализации
метод альфа-бета отсечения по-определению приводит к тому же решению, что и “чистый” алгоритм Минимакс. Чтобы проверить, не изменилась ли логика принятия решения (а точнее, результаты — ходы), я написал юнит-тест, в котором робот совершал по 8 ходов для каждого из 2-х соперников (16 ходов всего) и сохранял полученную серию ходов — с отключенной опцией отсечения.
Затем, в том же тесте, процедура повторялась при включенной опции отсечения. После чего последовательности ходов сравнивались. Расхождение в ходах говорит об ошибке реализации алгоритма альфа-бета отсечения (тест провален).
Затем, в том же тесте, процедура повторялась при включенной опции отсечения. После чего последовательности ходов сравнивались. Расхождение в ходах говорит об ошибке реализации алгоритма альфа-бета отсечения (тест провален).
Небольшая оптимизация алгоритма альфа-бета отсечения
С включенной в настройках AI опцией отсечения количество вершин в дереве позиций сократилось в среднем в 3 раза. Этот результат можно несколько улучшить.
В приведенном выше примере:

так удачно “совпало”, что, перед поддеревом с вершиной в позиции 3 мы рассмотрели поддерево с вершиной в позиции 2. Если бы очередность была иной, мы могли начать с “худшего” поддерева и не прийти к выводу об отсутствии смысла в рассмотрении очередной позиции.
Как правило, более “экономным” оказывается отсечение на дереве, вершины-потомки которого на одном уровне (т.е., все возможные ходы из i-позиции) уже отсортированы по текущей (без заглядывания вглубь) оценке позиции. Иначе говоря, мы предполагаем, что от лучшего (с точки зрения эвристики) хода больше вероятность получить лучшую итоговую оценку. Таким образом, мы, с некоторой вероятностью, отсортируем дерево так, что “лучшее” поддерево будет рассмотрено прежде “худшего”, что позволит отсечь больше вариантов.
Выполнение оценки текущей позиции — процедура затратная. Если прежде нам было достаточно оценить только терминальные позиции (листья), то сейчас оценка производится для всех вершин дерева. Однако, как показали тесты, суммарное количество произведенных оценок все равно оказалось несколько меньше, чем в варианте без первоначальной сортировки возможных ходов.
Особенности программной реализации
Алгоритм альфа-бета отсечения возвращает тот же ход, что и исходный алгоритм Минимакс. Это проверяет написанный нами юнит-тест, сравнивающий две последовательности ходов (для алгоритма с отсечением и без). Альфа-бета отсечение с сортировкой, в общем случае, может указать на другой ход в качестве квазиоптимального.
Чтобы протестировать корректную работу модифицированного алгоритма, нужен новый тест. Несмотря на модификацию, алгоритм с сортировкой должен выдавать ровно тот же итоговый вектор оценки ([3, 2] в примере на рисунке), что и алгоритм без сортировки, что и исходный алгоритм Минимакс.
В тесте я создал серию пробных позиций и выбрал из каждой по “лучшему” ходу, включая и отключая опцию сортировки. После чего сравнил полученные двумя способами вектора оценки.
Чтобы протестировать корректную работу модифицированного алгоритма, нужен новый тест. Несмотря на модификацию, алгоритм с сортировкой должен выдавать ровно тот же итоговый вектор оценки ([3, 2] в примере на рисунке), что и алгоритм без сортировки, что и исходный алгоритм Минимакс.
В тесте я создал серию пробных позиций и выбрал из каждой по “лучшему” ходу, включая и отключая опцию сортировки. После чего сравнил полученные двумя способами вектора оценки.
Дополнительно, раз уж позиции для каждого из возможных в текущей вершине дерева ходов отсортированы по эвристической оценке, напрашивается мысль сразу отбросить несколько худших вариантов. К примеру, шахматист может рассмотреть ход, на котором он подставляет свою ладью под удар пешки. Однако, “раскручивая” ситуацию вглубь на 3, 4 … хода вперед, он сразу отметет варианты, когда, к примеру, противник подставит под удар слона своего ферзя.
В настройках AI я задаю вектор “отсечения худших вариантов”. К примеру, вектор вида [0, 0, 8, 8, 4] означает, что:
- заглядывая на один [0] и два [0] шага вперед, программа рассмотрит все возможные ходы, т.к. 0 означает отсутствие отсечения,
- заглядывая на три [8] и четыре [8] шага вперед, программа рассмотрит до 8 “лучших” ходов, ведущих из очередной позиции, включительно,
- заглядывая на пять и более шагов вперед [4], программа оценит не более 4 “лучших” ходов.
Со включенной сортировкой для алгоритма альфа-бета отсечения и похожим вектором в настройках отсечения программа стала затрачивать на выбор квазиоптимального хода порядка 300 миллисекунд, “углубляясь” на 8 шагов вперед.
Оптимизация эвристики
Несмотря на приличное количество перебираемых в дереве позиций вершин и “глубокое” заглядывание вперед в поисках квазиоптимального хода, у AI оказалось несколько слабых мест. Одно из них я определил как “заячью ловушку”.
Заячья ловушка
Клетка зайца вносит в игру элемент случайности. Как правило (в 8 — 10 случаях из 15), случайность оказывается неприятной для игрока. Поэтому я определил следующие “эффекты” для клетки зайца при оценке и построении дерева позиций (не непосредственно в игре!):
Однако идея со штрафом на практике не сработала. Приведу пример:
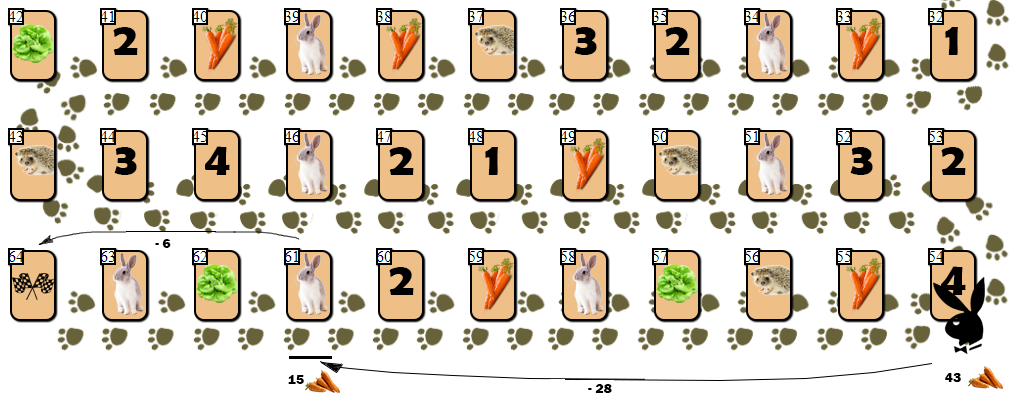
У игрока на клетке 54 недостаточно морковки (43), чтобы финишировать за один ход — ход на 10 клеток вперед потребовал бы 55 морковок. Но AI, невзирая на штрафы, делает ход на клетку зайца (61), затрачивая 28 моркови. С расчетом в дальнейшем совершить победный ход, потратив еще 6 морковок и сведя общее количество моркови на руках к 9 (допустимо финишировать с запасом не более 10 морковок).
Однако в игре, где конкретную карту зайца определяет случай (генератор БПСЧ), заяц с немалой вероятностью получит на руки дополнительную морковь, избавляясь от которой будет вынужден совершить еще 4 — 6 ходов. Как так получилось, что, невзирая на большой штраф в оценке позиции с клеткой зайца, AI совершил такой неоправданно рискованный ход?
Дело в том, что штраф определен для одного хода, для одной позиции. AI же смотрит на несколько ходов вперед. Штраф после первого хода на клетку зайца не участвует в финальной оценке, так как за ним следует ход, дающий максимально возможную оценку. В итоге я решил проблему “заячьей ловушки” следующим образом:
ход игрока на одну из финальных клеток с зайцем гарантированно приравнивает количество морковок на руках игрока к 65 — это один из “эффектов” клетки зайца, вероятно, худший из возможных в данной ситуации. После такого шага финишный ход сделать уже не получится, так как на руках имеется избыток моркови и требуется серия ходов назад, на ежа, с последующим ходом (ходами) вперед для завершения игры.
- ход на клетку зайца стабильно уменьшает количество морковок игрока на 7,
- при оценке позиции игрок, стоящий на клетке зайца, получает штраф. Штраф резко вырастает, если игрок, стоящий на клетке зайца, имеет возможность финишировать на следующем ходу.
Однако идея со штрафом на практике не сработала. Приведу пример:
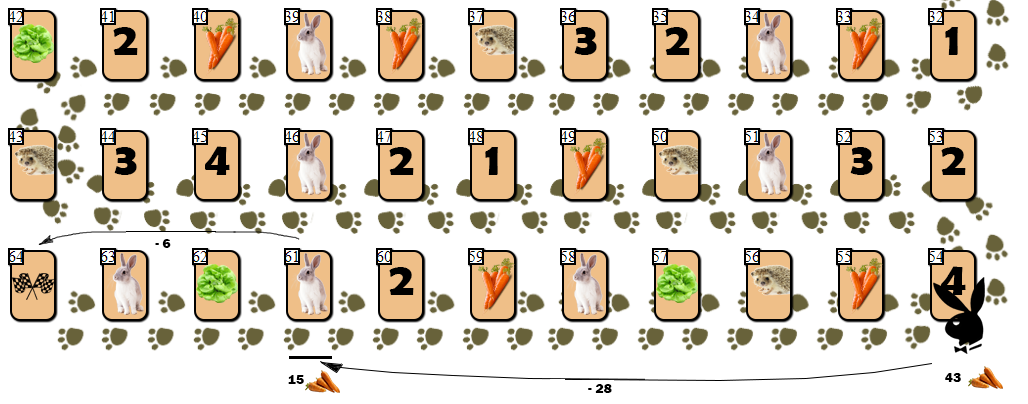
У игрока на клетке 54 недостаточно морковки (43), чтобы финишировать за один ход — ход на 10 клеток вперед потребовал бы 55 морковок. Но AI, невзирая на штрафы, делает ход на клетку зайца (61), затрачивая 28 моркови. С расчетом в дальнейшем совершить победный ход, потратив еще 6 морковок и сведя общее количество моркови на руках к 9 (допустимо финишировать с запасом не более 10 морковок).
Однако в игре, где конкретную карту зайца определяет случай (генератор БПСЧ), заяц с немалой вероятностью получит на руки дополнительную морковь, избавляясь от которой будет вынужден совершить еще 4 — 6 ходов. Как так получилось, что, невзирая на большой штраф в оценке позиции с клеткой зайца, AI совершил такой неоправданно рискованный ход?
Дело в том, что штраф определен для одного хода, для одной позиции. AI же смотрит на несколько ходов вперед. Штраф после первого хода на клетку зайца не участвует в финальной оценке, так как за ним следует ход, дающий максимально возможную оценку. В итоге я решил проблему “заячьей ловушки” следующим образом:
ход игрока на одну из финальных клеток с зайцем гарантированно приравнивает количество морковок на руках игрока к 65 — это один из “эффектов” клетки зайца, вероятно, худший из возможных в данной ситуации. После такого шага финишный ход сделать уже не получится, так как на руках имеется избыток моркови и требуется серия ходов назад, на ежа, с последующим ходом (ходами) вперед для завершения игры.
Поправочные коэффициенты
Ранее, приводя формулу эвристической оценки текущей позиции
E = Ks * S + Kc * C + Kp * P,
я упомянул, но не описал поправочные коэффициенты.
Дело в том, что, как сама формула, так и наборы функций
Как оценить “адекватность” оценки? Оценка — величина безразмерная, и сравнивать ее можно лишь с другой оценкой. Я смог придумать единственный один способ уточнения поправочных коэффициентов:
заложил в программу ряд “этюдов”, хранимых в CSV файле с данными вида
45;26;2;f;29;19;0;f;2
...
Эта строка означает буквально следующее:
- первый игрок находится на 45 клетке, на руках у него 26 карточек морковки и 2 карточки салата, игрок не пропускает ход (f = false). Право хода всегда за первым игроком.
- второй игрок на 29 клетке с 19 карточками морковки и без карточек салата, ход не пропускает.
- цифра два означает, что, “решая” этюд, я предположил, что второй игрок находится в выигрышной ситуации.
Заложив в программу 20 этюдов, я “загружал” их в игровом web-клиенте, а затем разбирал каждый этюд. Разбирая этюд, я поочередно совершал ходы за каждого из игроков, до тех пор, пока не определялся с “победителем”. Закончив оценку, я отправлял ее в специальной команде на сервер.
Оценив 20 этюдов (конечно, стоило бы разобрать их побольше), я произвел оценку каждого из этюдов программой. При оценке по очереди перебирались значения каждого из поправочных коэффициентов, от 0.5 до 2 с шагом 0.1 — итого
В итоге я выбрал те тройки, для которых процент “попаданий” был максимален (16 из 20). Вышло около 250 из 4096 векторов, из которых я отобрал “лучший”, опять же, “на глазок”, и установил его в настройках AI.
Итоги
Как результат, я получил рабочую программу, которая, как правило, обыгрывает меня в варианте один на один против компьютера. Серьезной статистики побед и поражений для актуальной версии программы пока не накопилось. Возможно, последующий легкий тюнинг AI сделает мои победы невозможными. Или практически невозможными, так как все еще остается фактор клетки зайца.
Например, в логике выбора оценки (абсолютный максимум или максимум относительно других игроков), я бы, определенно, попробовал промежуточный вариант. Как минимум, при равенстве абсолютной величины оценки i-го игрока, резонно выбрать ход, ведущий к позиции с большей относительной величиной оценки (гибрид благородного Лесли и коварного Фейта).
Программа вполне работоспособна для варианта с 3-я игроками. Однако есть подозрения, что “качество” ходов AI для игры с 3-я игроками ниже, чем для игры с двумя игроками. Впрочем, в ходе последнего теста я проиграл компьютеру — возможно, по неосторожности, небрежно оценивая количество моркови на руках и придя к финишу с избытком “топлива”.
Пока что дальнейшее развитие AI тормозит отсутствие человека — “тестировщика”, т.е., живого оппонента компьютерному “гению”. Сам я наигрался в Зайца и Ежа до тошноты и вынужден прерваться на текущем этапе.
→ Ссылка на репозиторий с исходниками