How to become an author
Search
Write a publication
Pull to refresh

Реализация алгоритма Левенберга-Марквардта для оптимизации нейронных сетей на TensorFlow

Reading time23 min
Views29K
Python*Mathematics*Machine learning*Artificial Intelligence
Tutorial

Это tutorial по библиотеке TensorFlow. Рассмотрим её немного глубже, чем в статьях про распознавание рукописных цифр. Это tutorial по методам оптимизации. Совсем без математики здесь не обойтись. Ничего страшного, если вы её совершенно забыли. Вспомним. Не будет никаких формальных доказательств и сложных выводов, только необходимый минимум для интуитивного понимания. Для начала небольшая предыстория о том, чем этот алгоритм может быть полезен при оптимизации нейронной сети.




Полгода назад друг попросил показать, как на Python сделать нейросеть. Его компания выпускает приборы для геофизических измерений. Несколько различных зондов в процессе бурения измеряют набор сигналов, связаных с параметрами окружающей скважину среды. В некоторых сложных случаях точно вычислить параметры среды по сигналам долго даже на мощном компьютере, а необходимо интерпретировать результаты измерений в полевых условиях. Возникла идея посчитать на кластере несколько сот тысяч случаев, и на них натренировать нейронную сеть. Так как нейросеть работает очень быстро, её можно использовать для определения параметров, согласующихся с измеренными сигналами, прямо в процессе бурения. Детали есть в статье:


Kushnir, D., Velker, N., Bondarenko, A., Dyatlov, G., & Dashevsky, Y. (2018, October 29). Real-Time Simulation of Deep Azimuthal Resistivity Tool in 2D Fault Model Using Neural Networks (Russian). Society of Petroleum Engineers. doi:10.2118/192573-RU


Одним вечером я показал, как keras реализовать простую нейронную сеть, и друг на работе запустил обучение на насчитанных данных. Через пару дней обсудили результат. С моей точки зрения он выглядел перспективно, но друг сказал, что нужны вычисления с точностью прибора. И если средняя квадратичная ошибка (mean squared error) получилась в районе 1, то нужна была 1е-3. На 3 порядка меньше. В тысячу раз.


Эксперименты с архитектурой нейронной сети, нормализацией данных, подходами к оптимизации не дали почти ничего. Через пару недель друг позвонил и сказал, что он установил MatLab и решил проблему методом Левенберга-Марквардта (далее будем называть LM). Оптимизировалось долго (несколько дней), не работало на GPU, но результат получился нужный. Это звучало как вызов.


Беглый поиск готового оптимизатора LM для keras или TensorFlow не дал результата. Наткнулся только на библиотеку pyrenn, но её функционал показался мне бедным. Решил реализовать самостоятельно. На первый взгляд выглядело всё просто, и двух вечеров должно было хватить. Провозился дольше. Проблемы оказалось две:


  1. TensorFlow. Куча статей, но практически все уровня «а давайте напишем hello world распознавалку рукописных цифр».
  2. Математика. Многое забыл, а авторы математических статей совершенно не заботятся о таких как я: сплошные формулы без объяснений, «очевидно!» и тд.

В итоге написал статью для забывших математику и желающих разобраться в TensorFlow чуть глубже, но без хардкора. В статье много текста и мало кода. Обратный вариант, когда мало текста и много кода, есть здесь Jupyter Notebook Levenberg-Marquardt.


Познакомимся с функцией Розенброка


Тренировочные данные будем генерировать функцией Розенброка, которую часто используют в качестве эталонного теста алгоритмов оптимизации:


$f(x, y) = (a-x)^2+b(y-x^2)^2$




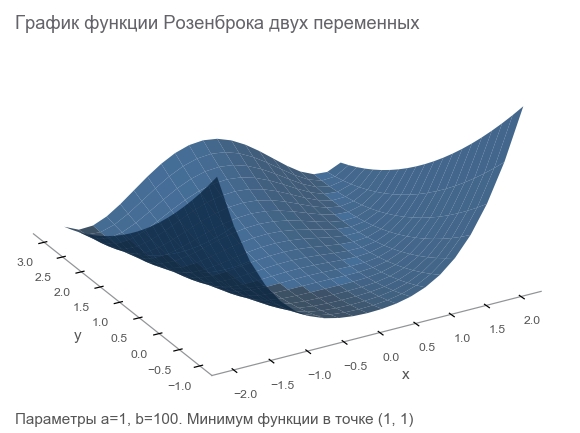
Чем же она хороша?


  • Красивый график. Называют долиной Розенброка и непереводимо Rosenbrock's banana function.
  • Глобальный минимум находится внутри длинной, узкой, параболической плоской долины. Найти долину тривиально, а глобальный минимум сложно.
  • Есть многомерный вариант. Придумать хорошую функцию многих переменных не так уж и просто.

С неё и начнём писать код подключив необходимые для дальнейшей работы библиотеки:


import numpy as np
import tensorflow as tf
import math

def rosenbrock(x, y, a, b):
    return (a - x)**2 + b*(y - x**2)**2

Сформулируем задачу


Раз уж мы говорили об измерительном приборе, давайте дальше использовать аналогию. Наш прибор в вымышленном мире умеет измерять координаты $(x, y)$ и высоту $z$. Физики изучили мир и заявили: "Да это же Розенброк! Зная координаты, можно точно вычислить высоту, вам не надо её измерять.". Иными словами, учёные дали нам модель $z = rosenbrock(x, y, a, b)$, которая зависит от параметров $(a, b)$. Эти параметры хоть и постоянны в вымышленном мире, но неизвестны. Их нужно найти.


Мы провели ряд экспериментов, которые дали $m$ точек $(x_1, y_1, z_1), (x_2, y_2, z_2),..., (x_m, y_m, z_m)$:


# (2.5, 2.5) - это реальные параметры, давайте забудем, что они нам известны
data_points = np.array([[x, y, rosenbrock(x, y, 2.5, 2.5)]
                       for x in np.arange(-2, 2.1, 2) 
                       for y in np.arange(-2, 2.1, 2)])
m = data_points.shape[0]

Первый способ оптимизации — попытаться угадать параметры. Воспользуемся библиотекой Numpy:


x, y = data_points[:, 0], data_points[:, 1]
z = data_points[:, 2]
# а вдруг а=5 и b=5?
a_guess, b_guess = 5., 5.
# Суффикс -hat используется для прогнозов, так проще ориентироваться,
# где реальные данные, а где то, что насчитала модель. В формулах
# соответствующие переменные будут иметь ^ треугольничек сверху -
# шляпку. Отсюда и суффикс hat.
z_hat = rosenbrock(x, y, a_guess, b_guess)

Как понять, насколько мы ошиблись? Посчитать невязки (residuals) — размеры ошибок. $m$ точек дают $m$ невязок — нужен интегральный показатель. Возведём каждую невязку в квадрат и посчитаем среднее:


$MSE(a, b) = \frac{1}{m}\sum_{i=1}^{m}(z_{i} - \widehat{z_{i}})^2$


Такая мера близости называется средняя квадратичная ошибка (mean squared error, далее будем называть mse):


# r - residuals (невязки)
r = z - z_hat
# mse
loss = np.mean(r**2)
print(loss)

[Out]: 3868.2291666666665

Минимизируя mse, мы решаем задачу о наименьших квадратах (nonlinear squares minimization):



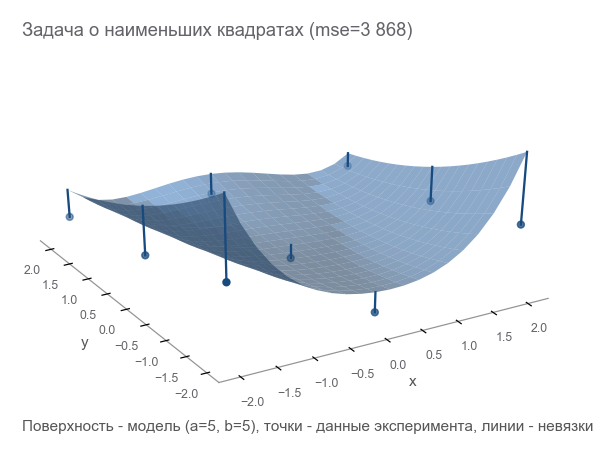
Видно, что параметры не угадали совершенно.


Сформулируем задачу на TensorFlow


Модель имеет вид $z = rosenbrock(x, y, a, b)$. Приведём её к виду $y = f(x, p)$ (обычно математики пишут $\beta$ вместо $p$, но программисты не используют бету). Теперь модель имеет вид $y = rosenbrock(x, p)$, где $y$ — высота, $x$ — вектор координат из двух элементов (компонент), а $p$ — вектор параметров.


Программисты часто думают о векторах, как об одномерных массивах. Это не совсем корректно. Массив чисел — это средство представления вектора. Представить вектор можно массивом размерностью $N$, двухмерным массивом $1\times N$, и даже массивом $N \times 1$ в тех случаях, когда важен факт, что вектор — это вектор-столбец (например, для умножения матрицы на него):


$ \begin{bmatrix} x_1\\\vdots \\ x_N \end{bmatrix} $


В TensorFlow используется понятие тензор. Тензор, как и массив, может быть одномерным (для представления вектора), двухмерным (для матрицы или вектора-столбца) и любой большей размерности.


# тензоры данных экспериментов ('placeholder' означает, что данные надо 
# передавать каждый раз при запуске вычислений)
x = tf.placeholder(tf.float64, shape=[m, 2])
y = tf.placeholder(tf.float64, shape=[m])
# тензор параметров ('variable' означает, что он хранит состояние)
# инициализируем его нашей догадкой (5, 5)
p = tf.Variable([5., 5.], dtype=tf.float64)
# модель
y_hat = rosenbrock(x[:, 0], x[:, 1], p[0], p[1])
# невязки
r = y - y_hat
# mse (mean squared error)
loss = tf.reduce_mean(r**2)

Код на TensorFlow по форме не отличается от кода на Numpy. По содержанию отличия огромные. Код на Numpy производит вычисление значения mse. Код на TensorFlow не производит никаких вычислений вообще, он формирует граф потока данных (dataflow graph), который может вычислить mse. Очень выносящий мозг момент — работа функции rosenbrock. Мы её используем в обоих случаях. Но когда передаём массивы Numpy, она производит вычисления по формуле и возвращает числа. А когда передаём тензоры TensorFlow, формирует подграф потока данных и возвращает его ребро (edge) в виде тензора. Чудеса полиморфизма, но не стоит ими злоупотреблять:



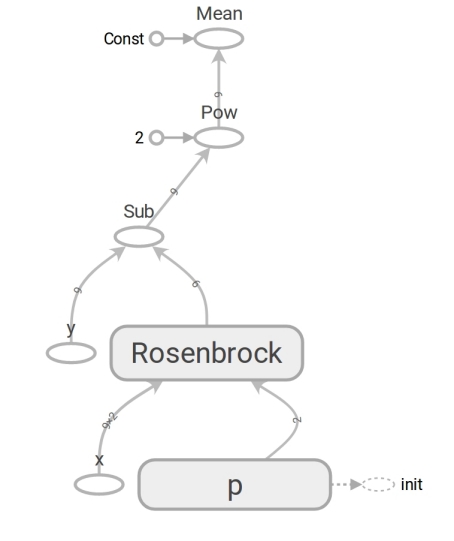
Благодаря наличию такого графа потока данных, TensorFlow в частности умеет вычислять производные автоматически (техникой reverse mode automatic differentiation).


Минутка математики. Блоки "для тех, кто забыл" буду прятать в спойлер.


Производная (число вошло - число вышло)

Скорее всего вы помните определение производной скалярной (возвращающей число) функции одной переменной: для $f:\mathbb{R}\rightarrow \mathbb{R}$, производная $f$ в точке $x\in \mathbb{R}$ определяется как:


${f}'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$


Производные — это способ измерения изменений. В скалярном случае производная показывает, насколько изменится функция $f$, если $x$ изменится на небольшое значение $\varepsilon $:


$f(x+\varepsilon)\approx f(x)+\varepsilon {f}'(x)$


Для удобства в дальнейшем обозначим $y=f(x)$, а производную $y$ по $x$ запишем как $\frac{\partial y}{\partial x}$. Такая запись подчёркивает, что $\frac{\partial y}{\partial x}$ — скорость изменения между переменными $x$ и $y$. Конкретнее, если $x$ изменится на $\varepsilon $, то $y$ изменится приблизительно на $\varepsilon \frac{\partial y}{\partial x}$. Ещё можно записать это так:


$x\rightarrow x+\Delta x\Rightarrow y\rightarrow \approx y+\frac{\partial y}{\partial x}\Delta x$


Читается как: "меняя $x$ на $x+\Delta x $ меняем $y$ на приблизительно $y + \Delta x \frac{\partial y}{\partial x}$". Такая запись наглядно подчёркивает связь между изменением $x$ и изменением $y$.


Мы построили граф потока данных, давайте запустим вычисление mse:


# при запуске вычислений нам надо передать данные 
# для подстановки в тензоры типа placeholder (координаты и высота)
feed_dict = {x: data_points[:,0:2], y: data_points[:,2]}
# в сессии запускаются операции и вычисления TensorFlow
session = tf.Session()
# инициализируем глобальные переменные графа
session.run(tf.global_variables_initializer())
# запускаем вычисление (оценку) тензора loss (mse)
current_loss = session.run(loss, feed_dict)
print(current_loss)

[Out]: 3868.2291666666665

Получился тот же результат, что и с Numpy. Значит не ошиблись.


Начнём оптимизировать


К сожалению угадать параметры не получилось. Но зато мы:


  1. Задали критерий оптимальности — минимальное значение mse.
  2. Определили варьирующие параметры: вектор $p$ с компонентами $a$, $b$ функции Розенброка.
  3. Пока не подумали про ограничения, но их нет.

На прошлом шаге мы сконструировали граф потока данных с конечным тензором loss (функция потерь). Цель оптимизации — найти значение вектора параметров $p$, при котором значение функции потерь минимальное. Нам повезло, график этой функции очень простой (вогнутый и без локальных минимумов):



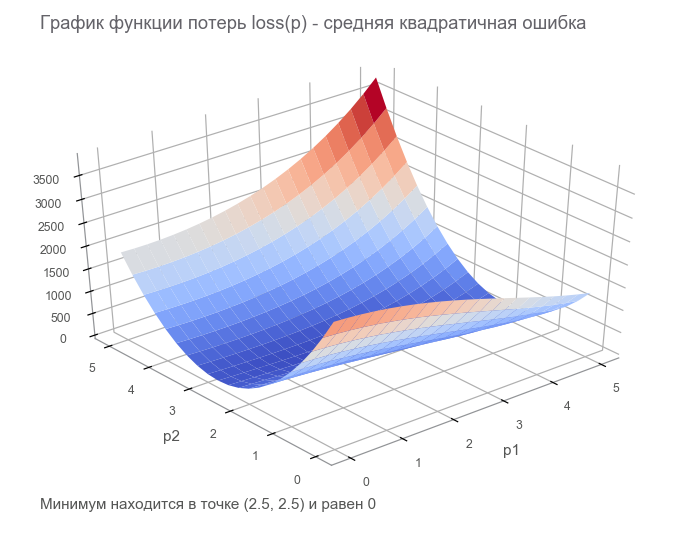
Приступаем к оптимизации. Для начала напишем обобщённый цикл:


# параметры: целевое значение mse, максимальное число шагов, тензор
# для вычисления mse, операция шага оптимизации и данные для тензоров placeholder
def train(target_loss, max_steps, loss_tensor, train_step_op, inputs):
    step = 0
    current_loss = session.run(loss_tensor, inputs)
    # оптимизируем пока не закончились шаги или не добились нужного результата
    while current_loss > target_loss and step < max_steps:
        step += 1
        # логируем прогресс на 1, 2, 4, 8, 16... шагах
        if math.log(step, 2).is_integer():
            print(f'step: {step}, current loss: {current_loss}')
        # делаем оптимизационный шаг
        session.run(train_step_op, inputs)
        current_loss = session.run(loss_tensor, inputs)
    print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}')

Оптимизируем методом наискорейшего градиентного спуска (SGD)


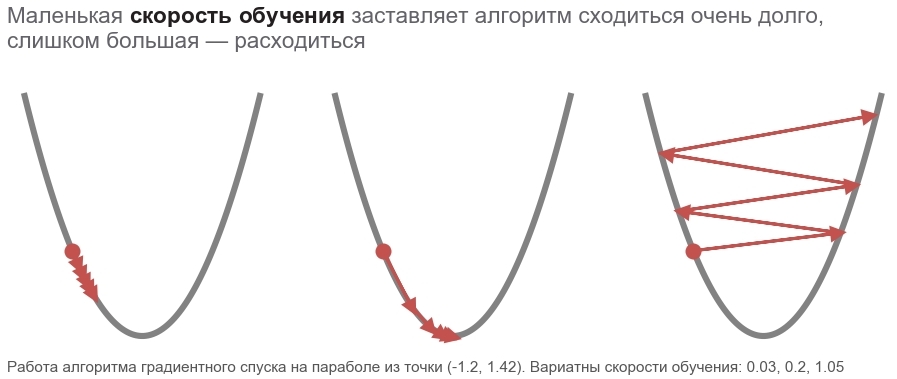
Действия этого метода можно сравнить с ездой дерзкого горнолыжника, который всегда ставит лыжи по линии падения склона (в самом крутом направлении вниз). При этом учитывает только уклон в точке нахождения. И если уклон сильный, то до следующего перестроения лыжник пролетает большое расстояние. При слабом же уклоне движется маленькими шагами. Может как улететь в дерево (алгоритм расходится), так и застрять в яме (локальном минимуме).



Записать можно так (меняем $\boldsymbol{p}$ на $\boldsymbol{p} - ...$):


$\boldsymbol{p} \rightarrow \boldsymbol{p}-\alpha [\nabla_{p} loss(\boldsymbol{p})]$


Жирное $\boldsymbol{p}$ подчёркивает, что это точка фактического нахождения — значение вектора параметров на текущем шаге. На первом шаге это наша догадка (5, 5). В формуле есть два интересных момента: $\alpha$ — скорость обучения (learning rate), $\nabla_{p} loss$ — градиент (gradient) функции потерь по вектору параметров.



Градиент (вектор вошёл - число вышло)

Рассмотрим функцию, которая принимает на вход вектор, а выдаёт скаляр: $f:\mathbb{R}^{N}\rightarrow \mathbb{R}$. Производная $f$ в точке $x\in \mathbb{R}^{N}$ теперь называется градиентом и является вектором $[\nabla_{x}f(x)]\in \mathbb{R}^{N}$ (читается как "на́бла"), составленным из частных производных (partial derivatives):


$\nabla_{x}y = (\frac{\partial y}{\partial x_{1}},\frac{\partial y}{\partial x_{2}},...,\frac{\partial y}{\partial x_{N}})$


Для этого случая запись зависимости изменения функции от изменения аргумента имеет такой вид:


$x\rightarrow x+\Delta x\Rightarrow y\rightarrow \approx y+\nabla_{x}y\cdot \Delta x$


Запись изменилась совсем немного, чтобы учесть, что $x$, $\Delta x$ и $\nabla_{x}y$ — векторы в $\mathbb{R}^{N}$, а $y$ — скаляр. При умножении векторов $\nabla_{x}y$ и $\Delta x$ используется скалярное произведение (сумма произведений компонент).


# вычисляем градиент функции потерь по вектору параметров
grad = tf.gradients(loss, p)[0]
# скорость обучения
learning_rate = 0.0005
# оптимизатор нам нужен, чтобы воспользоваться его методом apply_gradients -
# обновление вектора параметров на градиент со знаком минус
opt = tf.train.GradientDescentOptimizer(learning_rate=1)
# сдвигаем вектор параметров на значение градиента с учётом скорости обучения
sgd = opt.apply_gradients([(learning_rate*grad, p)])
# запускаем цикл оптимизации, сделаем не больше 40000 шагов
session.run(tf.global_variables_initializer())
train(1e-10, 40000, loss, sgd, feed_dict)
print('PARAMETERS:', session.run(p))

[Out]: step: 1, current loss: 3868.2291666666665
       step: 2, current loss: 1381.5379689135807
       [...]
       ENDED ON STEP: 582, FINAL LOSS: 9.698531012270816e-11
       PARAMETERS: [2.50000205 2.49999959]

Потребовалось 582 шага:



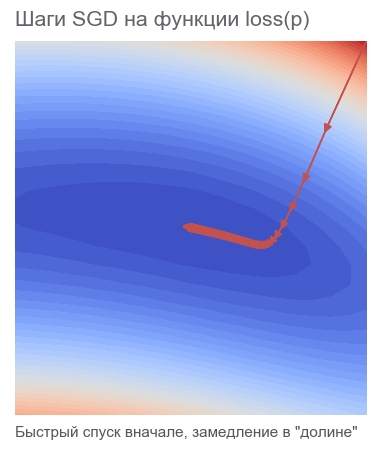
Движение в направлении антиградиента

Почему движемся в обратном градиенту направлении? Вспомним запись со скалярным произведением: $x\rightarrow x+\Delta x\Rightarrow y\rightarrow \approx y+\nabla_{x}y\cdot \Delta x$. Минимизируем $y$. Так как известно поведение функции только в малой окрестности через производную, надо двигаться мелкими, но оптимальными шагами, минимизиуя произведение $\nabla_{x}y\cdot \Delta x$. По школьному определению скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними: $a \cdot b = \left |a \right |\left |b \right |cos\angle (a,b)$. При фиксированной длине векторов это произведение достигает минимума при косинусе равном -1, т.е. при угле 180 градусов, когда вектора направлены в противоположные стороны. Соответственно минимум скалярного произведения $\nabla_{x}y\cdot \Delta x $ достигается при $\Delta x $ в направлении антиградиента.


Оптимизируем методом Adam


Не будем дальше углубляться в градиентные методы, но вариаций есть масса. Почитать про них можно в статье Методы оптимизации нейронных сетей. В TensorFlow многие оптимизаторы уже реализованы. Например, Adam:


# не будем сами вычислять и применять градиенты, 
# а сразу сконструируем шаг оптимизации
adm = tf.train.AdamOptimizer(15).minimize(loss)
# запускаем цикл оптимизации, сделаем не больше 40000 шагов
session.run(tf.global_variables_initializer())
train(1e-10, 40000, loss, adm, feed_dict)
print('PARAMETERS:', session.run(p))

[Out]: step: 1, current loss: 3868.2291666666665
       step: 2, current loss: 34205.72916492336
       [...]
       ENDED ON STEP: 317, FINAL LOSS: 2.424142714263483e-12
       PARAMETERS: [2.49999969 2.50000008]

Справились за 317 шагов. Гораздо быстрее.


Оптимизируем методом Ньютона


Действия методов второго порядка можно сравнить с ездой разумного сноубордиста-фрирайдера, который долго обдумывает следующую точку своего маршрута и учитывает не только уклон в точке нахождения, но и кривизну.



Фактически, и методы градиентного спуска, и методы второго порядка пытаются угадать (аппроксимировать) функцию по текущей точке. Градиентные методы ориентируются только на уклон (slope) графика функции в точке — первую производную. Методы же второго порядка кроме уклона учитывают и кривизну (curvature) — вторую производную: "если кривизна сохранится, то где будет минимум?". Вычисляем и направляемся туда:



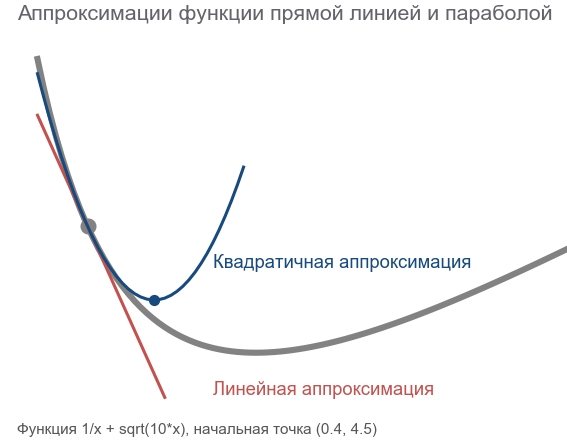
Построить такую аппроксимацию и вычислить предполагаемую точку минимума можно с помощью ряда Тейлора (Taylor series). Для одномерного случая аппроксимация полиномом второго порядка в точке $a$ выглядит так:


$f(x) \approx f(a) + \frac{f'(a)(x-a)}{1!} + \frac{f''(a)(x-a)^2}{2!}$


Минимум достигается при $x = a - \frac{f'(a)}{f''(a)}$. Многомерный случай выглядит более серьёзно:



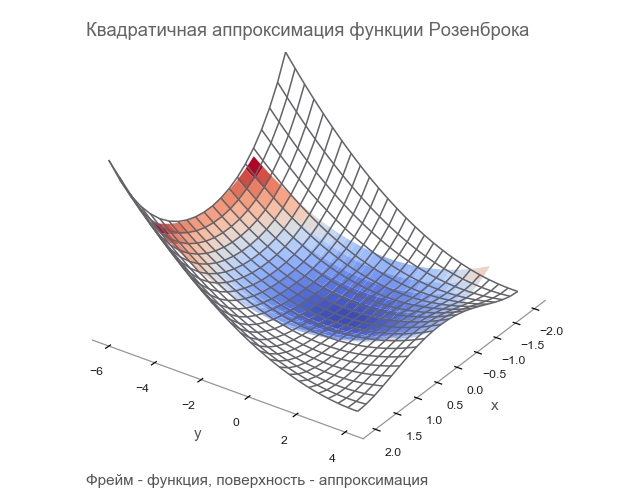
Матрица Гессе (вектор вошёл - число вышло)

Матрица Гессе (Hessian matrix) — это квадратная матрица, составленная из вторых производных:


$\boldsymbol{H}y_{x} = \begin{bmatrix} \frac{\partial^2y}{\partial x_1^2} & \frac{\partial^2y}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2y}{\partial x_1 \partial x_N} \\ \frac{\partial^2y}{\partial x_2 \partial x_1} & \frac{\partial^2y}{\partial x_2^2} & \cdots & \frac{\partial^2y}{\partial x_2 \partial x_N} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2y}{\partial x_N \partial x_1} & \frac{\partial^2y}{\partial x_N \partial x_2} & \cdots & \frac{\partial^2y}{\partial x_N^2} \end{bmatrix}$


Аппроксимация полиномом второго порядка для функции от вектора через градиент и матрицу Гессе в точке $a$ выглядит так:


$f(x) \approx f(a) + (x-a)^\intercal [\nabla_{x}f(a)] + \frac{1}{2!}(x-a)^\intercal [\boldsymbol{H}f_{x}(a)](x-a)$


Минимум достигается при $x =a - [\boldsymbol{H}f_{x}(a)]^{-1}[\nabla_{x}f(a)]$. Форма практически совпадает с одномерным случаем: заменили первую производную на градиент, вторую на матрицу Гессе и сделали поправку на работу с векторами. Делить вектор на матрицу нельзя, поэтому используется умножение на обратную (inverse) матрицу. Т означает транспонирование (transpose). В формуле подразумевается, что по умолчанию вектор — это столбец. Транспонирование превращает вектор-столбец в вектор-строку. При реализации на TensorFlow надо это учитывать, но в обратную сторону: по умолчанию вектор — это строка (одномерный тензор). На всякий случай: транспонирование — это не поворот на 90 градусов, это превращение строк в столбцы в том же порядке.


Итак, шаг метода Ньютона имеет следующий вид:


$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{H}loss_{p}(\boldsymbol{p})]^{-1}[\nabla_{p}loss(\boldsymbol{p})]$


В TensorFlow есть всё для реализации этого метода:


# матрица Гессе для функции потерь по параметрам 
hess = tf.hessians(loss, p)[0]
# градиент превращаем в вектор-столбец
grad_col = tf.expand_dims(grad, -1)
# вычислим, насколько надо изменить вектор параметров
dp = tf.matmul(tf.linalg.inv(hess), grad_col)
# конвертируем вектор-столбец в вектор-строку
dp = tf.squeeze(dp)
# сдвигаем p на dp со знаком минус
newton = opt.apply_gradients([(dp, p)])
# запускаем цикл оптимизации, сделаем не больше 40000 шагов
session.run(tf.global_variables_initializer())
train(1e-10, 40000, loss, newton, feed_dict)
print('PARAMETERS:', session.run(p))

[Out]: step: 1, current loss: 3868.2291666666665
       step: 2, current loss: 105.04357496954218
       step: 4, current loss: 9.96663526704236
       ENDED ON STEP: 6, FINAL LOSS: 5.882202372519996e-20
       PARAMETERS: [2.5 2.5]

Хватило 6 шагов:



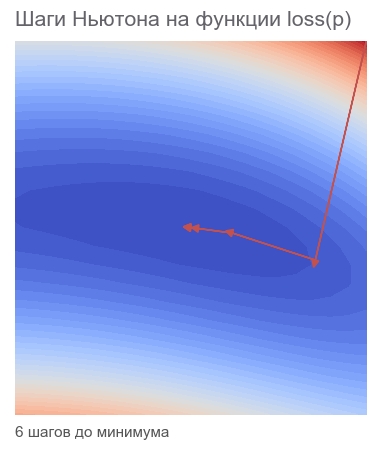
Оптимизируем алгоритмом Гаусса-Ньютона


В методе Ньютона есть один недостаток — матрица Гессе. Благодаря TensorFlow мы можем посчитать её в одну строку кода. Согласно wiki, первое упоминание о своём методе Иоганн Карл Фридрих Гаусс сделал в 1809 году. Вычисление матрицы Гессе для нескольких параметров для метода наименьших квадратов тогда могло занять кучу времени. Сейчас можно считать, что алгоритм Гаусса-Ньютона использует аппроксимацию матрицы Гессе через матрицу Якоби, чтобы упростить вычисления. Но с точки зрения истории это не так: Людвиг Отто Гессе (который разработал матрицу, названную в честь него) родился 1811 году — через 2 года после первого упоминания алгоритма. А Карлу Густаву Якоби было 5 лет.


Алгоритм Гаусса-Ньютона не работает с функцией потерь. Он работает с функцией невязок $r(p)$. Эта функция принимает на вход вектор параметров $p$ и возвращает вектор невязок (residuals). В нашем случае, вектор $p$ состоит из 2 компонент (параметры $a$ и $b$ функции Розенброка), а вектор невязок из $m$ компонент (по числу экспериментов). Получается векторная функция векторного аргумента. Её производная:


Матрица Якоби (вектор вошёл - вектор вышел)

Рассмотрим функцию, которая на вход принимает вектор и выдаёт тоже вектор: $f:\mathbb{R}^{N}\rightarrow \mathbb{R}^{M}$. Производная $f$ в точке $x$ теперь имеет размер $N\times M$, называется матрицей Якоби, и состоит из всех комбинаций частных производных:


$\boldsymbol{J}y_{x} = \begin{pmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{N}}\\ \vdots & \ddots & \vdots \\ \frac{\partial y_{M}}{\partial x_{1}} & \cdots & \frac{\partial y_{M}}{\partial x_{N}} \end{pmatrix}$


Можно заметить, что строками матрицы Якоби являются градиенты компонентов $y$. Элемент $(i, j)$ матрицы $\frac{\partial y}{\partial x}$ равен $\frac{\partial y_{i}}{\partial x_{j}}$ и говорит нам, насколько изменится $y_{i}$, при изменении $x_{j}$ на небольшое значение. Как и в предыдущих случаях можно записать:


$x\rightarrow x+\Delta x\Rightarrow y\rightarrow \approx y+\boldsymbol{J}y_{x}\Delta x$


Здесь $\boldsymbol{J}y_{x}$ матрица $N\times M$, а $\Delta x$ вектор размера $N$, таким образом произведение $\boldsymbol{J}y_{x}\Delta x$ — это произведение матрицы на вектор, в результате которого получается вектор размера $M$.


Чтобы не путаться в обилии символов, будем считать, что $\boldsymbol{J}_{r}$ — матрица Якоби функции невязок в текущей точке $\boldsymbol{p}$. Тогда алгоритм Гаусса-Ньютона можно записать так:


$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$


Запись по форме полностью совпадает с записью метода Ньютона. Только вместо матрицы Гессе используется $\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}$, а вместо градиента $\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$. Далее посмотрим, почему можно использовать такую аппроксимацию. Пока же приступим к реализации на TensorFlow:


# к сожалению, в TensorFlow нет реализации вычисления матрицы Якоби,
# но мы помним, что эта матрица состоит из градиентов компонентов 
# функции невязок. В итоге, матрица вычисляется так:
# 1) разбиваем функцию невязок на отдельные компоненты tf.unstack(r)
# 2) для каждого компонента вычисляем градиент tf.gradients(r_i, p)
# 3) объединяем все градиенты в одну матрицу tf.stack
# такой способ вычисления не очень эффективный, более того мы очень 
# сильно увеличиваем размер графа потока данных
j = tf.stack([tf.gradients(r_i, p)[0]
              for r_i in tf.unstack(r)])
jT = tf.transpose(j)
# вектор невязок переводим в вектор-столбец
r_col = tf.expand_dims(r, -1)
# аппроксимация матрицы Гессе и градиента
hess_approx = tf.matmul(jT, j)
grad_approx = tf.matmul(jT, r_col)
# вычислим, насколько надо изменить вектор параметров
dp = tf.matmul(tf.linalg.inv(hess_approx), grad_approx)
# конвертируем вектор-столбец в вектор-строку
dp = tf.squeeze(dp)
# сдвигаем p на dp со знаком минус
ng = opt.apply_gradients([(dp, p)])
# запускаем цикл оптимизации, сделаем не больше 40000 шагов
session.run(tf.global_variables_initializer())
train(1e-10, 40000, loss, ng, feed_dict)

[Out]: step: 1, current loss: 3868.2291666666665
       step: 2, current loss: 14.653025157673625
       step: 4, current loss: 4.3918079172783016e-07
       ENDED ON STEP: 4, FINAL LOSS: 3.374364957618591e-17
       PARAMETERS: [2.5 2.5]

Хватило 4х шагов. Меньше чем для метода Ньютона.



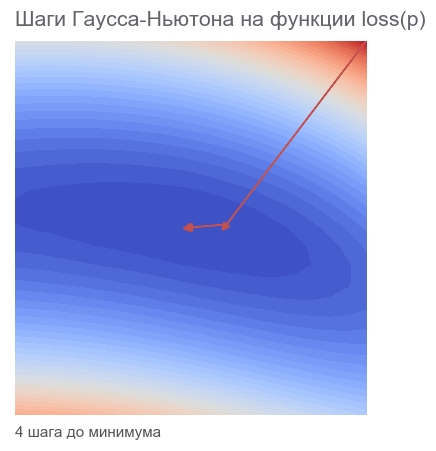
Как видно из кода, функция потерь не используется при оптимизации, только для критерия остановки и логирования. Как же оптимизационный алгоритм узнаёт, какую функцию минимизировать? Ответ удивителен: никак! Гаусс-Ньютон минимизирует только mean squared error.


Закрепим математическую часть статьи


Мы повторили всю необходимую нам математику. Давайте немного закрепим, чтобы дальше сконцентрироваться только на программировании и TensorFlow. Возможно вам понадобится карандаш, чтобы проследить последовательность математических действий.


Есть модель $y=f(x,p)$, где $x$ — вектор, $p$ — вектор параметров размерности $n$, а $y$ — скаляр. Из экспериментов получили $m$ точек $(x_{1}, y_{1}), ..., (x_{m}, y_{m})$ (data pairs). Векторная функция невязок зависит только от вектора параметров: $r(p) = (r_{1}(p), ... r_{m}(p))$, где $r_{k}(p) = y_{k} - \widehat{y_{k}} = y_{k} - f(x_{k}, p)$. Может возникнуть вопрос, почему функция невязок зависит только от $p$, ведь в формуле есть и $x_{k}, y_{k}$? Дело в том, что $x_{k}, y_{k}$ уже известны из экспериментов и зафиксированы, и только вектор параметров является переменным.


Надо найти такое значение вектора параметров $p$, чтобы сумма квадратов невязок (sum of squared error — sse или residual sum-of-squares — rss) была минимальная. Вместо привычной нам mse мы будем использовать sse, чтобы не таскать везде деление на $m$. Эти две функции достигают своего минимума на одном и том же векторе параметров. Наша функция потерь имеет вид:


$loss(p) = r_{1}^2(p) + \cdots + r_{m}^2(p) = \sum_{k=1}^{m} r_{k}^2(p)$


Далее для простоты нигде не будем писать $p$ в скобочках $(p)$.


Чтобы воспользоваться методом Ньютона, нам нужен градиент этой функции и матрица Гессе. Градиент — это вектор частных производных. Производная суммы — это сумма производных, а производная квадрата функции $r^2$ равна $2r \frac{\partial r}{\partial p}$. Таким образом получаем:


$\nabla_{p}loss = (\sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{1}}, \cdots, \sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{n}}) $


Матрица Гессе состоит из всех комбинаций вторых производных. Ячейка матрицы Гессе имеет такой вид:


$[\boldsymbol{H}loss_{p}]_{ij} = \frac{\partial^2 loss}{\partial p_{i} \partial p_{j}} = \sum_{k=1}^{m}(2\frac{\partial r_{k}}{\partial p_{i}}\frac{\partial r_{k}}{\partial p_{j}} + 2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}})$


Матрица эта диагонально симметричная. При её вычислении мы воспользовались теми же правилами, что и при вычислении градиента, плюс школьной формулой ${(uv)}'={u}'v+u{v}'$.
Отлично! Мы можем воспользоваться методом Ньютона.


Заметим, что в формуле для матрицы Гессе есть часть, которая уменьшается по мере приближения к минимуму, — слагаемое $2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$. Чем ближе к минимуму, тем меньше невязка, тем меньше $r_{k}$, а следовательно и всё произведение. И именно этот компонент доставляет больше всего вычислительных неприятностей — он содержит настоящую вторую производную. А что будет, если этот компонент откинуть? Мы получим алгоритм Гаусса-Ньютона.


Для него нужна матрица Якоби:


$\boldsymbol{J}_{r} = \begin{pmatrix} \frac{\partial r_{1}}{\partial p_{1}} & \cdots & \frac{\partial r_{1}}{\partial p_{n}}\\ \vdots & \ddots & \vdots \\ \frac{\partial r_{m}}{\partial p_{1}} & \cdots & \frac{\partial p_{m}}{\partial p_{n}} \end{pmatrix}$


Согласитесь, она выглядит гораздо проще, чем градиент и матрица Гессе. Заметим, что:


$2\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r} \approx \boldsymbol{H}loss_{p}$


Заметить это "глазами" не так уж и просто. Лучше взять карандаш и начать производить матричное умножение (строка умножается на столбец). Тогда будет лучше видно, что результат — это выражение для матрицы Гессе без компонента $2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$, который мы и хотели откинуть.
С градиентом ещё проще (надо умножить матрицу на вектор):


$2\boldsymbol{J}_{r}^\intercal r = \nabla_{p}loss$


Таким образом, у нас сошлось утверждение, что алгоритм Гаусса-Ньютона — это метод Ньютона с аппроксимацией матрицы Гессе через матрицу Якоби, который работает только с функцией потерь mse.


Переформулируем и усложним задачу


Вымышленный прибор измерял координаты и высоту. Мы решили упростить железо, измерять только координаты, а высоту вычислять. Провели $m$ экспериментов $(x_{1}, y_{1}), ..., (x_{m}, y_{m})$, физики дали модель $y = rosenbrock(x, p)$. Разными методами оптимизации мы успешно нашли значение вектора параметров $p$, при котором модель работает достаточно точно.


А теперь представьте, что учёные отказались давать модель: "Мы совершенно не представляем физику вашего вымышленного мира. Давайте как-нибудь сами!". В ситуациях, когда недостаточно знаний о природе вещей, или эта природа слишком сложная, можно попробовать решить задачу техникой машинного обучения (supervised learning). Например, с помощью нейронной сети. Такое решение имеет свою цену: данные (training set) — их надо много; сложность интерпретации — не всегда понятно почему модель (prediction model) работает или не работает; проблемы экстраполяции — модель стабильно работает только на данных из того же распределения, что и обучающая выборка.


В статье будем использовать многослойный перцептрон (multi-layer perceptron neural network или mlp). Есть аспекты, которые не будем учитывать в статье, но которые необходимо учитывать в реальной работе:


  • Начальные значения (starting values) весов. Будем инициализировать веса алгоритмом Xavier'a, но наверняка есть и более удачные варианты.
  • Переобучение (overfitting). Тема статьи — методы оптимизации. А их задача искать минимум, несмотря ни на что. А задача разработчика — не допустить переобучения.
  • Масштабирование входных данных (scaling of the input). Не будем делать, но это может значительно улучшить результат.

В прошлый раз хватило 9 экспериментов. В этот раз проведём 500:


# эксперименты будут случайными
def get_random_rosenbrock_data_points(m):
    result = np.zeros((m, 3))
    result[:, 0] = np.random.uniform(-2, 2, m)
    result[:, 1] = np.random.uniform(-2, 2, m)
    result[:, 2] = rosenbrock(result[:, 0], result[:, 1], 2.5, 2.5)
    return result

m = 500
data_points = get_random_rosenbrock_data_points(m)
# overfitting не тема статьи, но совсем без валидации нельзя
validation_data_points = get_random_rosenbrock_data_points(m)

Из экспериментов получили 500 точек. Наша задача — ничего не зная о функции Розенброка обучить модель (learner), которая будет прогнозировать высоту (outcome measurement) по координатам (features) для новых ещё неизвестных данных.


Реализуем однослойный перцептрон


Часто структуру перцептрона рисуют в виде кружочков со стрелочками (network diagram). Мне больше нравится такой вариант визуализации от MatLab:



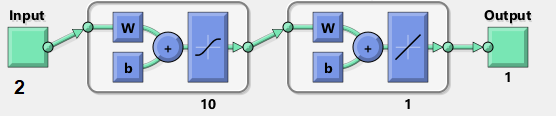
Вектор из двух компонент подаётся на вход (input). Он умножается на матрицу весов $W$ (weights) размера 2x10, к результату прибавляется вектор смещения $b$ (bias) размера 10, и результат передаётся нелинейной функции активации (activation). Так получается первый (единственный) скрытый уровень (hidden layer) из 10 нейронов. Во втором блоке к нему применяется другая матрица весов, другой вектор смещения, и уже без нелинейной функции получается скалярный результат (output).


Самая удобная запись, на мой взгляд, такая (будем использовать $tanh$):


$\begin{matrix} h_{1} = tanh(xW_{1} + b_{1})\\ \widehat{y} = h_{1}W_{2} + b_{2} \end{matrix} $


Или подробнее:


$h_1 = tanh(\begin{bmatrix} x_1 & x_2 \end{bmatrix}\begin{bmatrix} w^{(1)}_{1,1} & \cdots& w^{(1)}_{1,10} \\ w^{(1)}_{2,1} &\cdots& w^{(1)}_{2,10} \end{bmatrix} + \begin{bmatrix} b^{(1)}_1 & \cdots & b^{(1)}_{10} \end{bmatrix}) \\ \widehat{y} = \begin{bmatrix}h^{(1)}_1 & \cdots & h^{(1)}_{10}\end{bmatrix} \begin{bmatrix} w^{(2)}_{1,1} \\ \vdots \\ w^{(2)}_{1,10} \\ \end{bmatrix} + b_2 $


Здесь используются матричные операции. Размерность $W_{1}$ однозначно определяется размерностью входного вектора и желаемой "шириной" скрытого уровня $h_{1}$, а из неё однозначно определяется размерность вектора-столбца $W_{2}$. Получили 41 параметр. Регулируя количество скрытых слоёв и их ширину, можно изменять количество параметров.


Если входной вектор заменить на матрицу $m \times 2$, то за один проход можно вычислить прогнозы для всех точек. Результатом буде вектор-столбец $\widehat{y}$ из $m$ компонентов:


# хотим скрытый слой из 10 "нейронов"
n_hidden = 10
# начальную догадку будем конструировать алгоритмом Xavier'a
initializer = tf.contrib.layers.xavier_initializer()

# тензоры данных экспериментов
x = tf.placeholder(tf.float64, shape=[m, 2])
y = tf.placeholder(tf.float64, shape=[m, 1])

# тензоры весов и смещения для вычисления скрытого слоя
W1 = tf.Variable(initializer([2, n_hidden], dtype=tf.float64))
b1 = tf.Variable(initializer([1, n_hidden], dtype=tf.float64))
# вычисление скрытого слоя, используем tanh для активации
h1 = tf.nn.tanh(tf.matmul(x, W1) + b1)
# тензоры весов и смещения для вычисления прогноза
W2 = tf.Variable(initializer([n_hidden, 1], dtype=tf.float64))
b2 = tf.Variable(initializer([1], dtype=tf.float64))
# вычисление прогноза
y_hat = tf.matmul(h1, W2) + b2
# невязки
r = y - y_hat
# также используем mse в качестве функции потерь
loss = tf.reduce_mean(tf.square(r))

# данные для подстановки в тензоры placeholder
feed_dict = {x: data_points[:,0:2], 
             y: data_points[:,2:3]}
validation_feed_dict = {x: validation_data_points[:,0:2], 
                        y: validation_data_points[:,2:3]}

Обучим нейросеть методом Adam


Обучение нейронной сети оптимизатором Adam ничем не отличается от поиска параметров для модели $rosenbrock$. Добавим подсчёт mse для валидационной выборки в конце:


# сконструируем шаг оптимизации
adm = tf.train.AdamOptimizer(1e-2).minimize(loss)
session.run(tf.global_variables_initializer())
# запускаем цикл оптимизации, сделаем не больше 40000 шагов
train(1e-10, 40000, loss, adm, feed_dict)
print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict)))

[Out]: step: 1, current loss: 671.4242576535694
       [...]
       ENDED ON STEP: 40000, FINAL LOSS: 0.22862158574440725
       VALIDATION LOSS: 0.29000289644978866

У вас могут получиться совершенно другие числа. Они во многом зависят от удачи: случайная инициализация весов, тренировочных данных, данных для валидации.


Вычислим матрицу Якоби для нейронной сети


Для модели $rosenbrock$ матрица Якоби вычислялась в 2 строки кода. Теперь ситуация сильно усложнилась:


  • Данные. Раньше было 9 экспериментов, теперь 500. Старым методом граф потока данных будет конструироваться долго.
  • Параметры. Раньше был вектор-строка параметров $p$, теперь параметры распределены по разным тензорам всевозможной формы.

Соответственно реализация усложнилась тоже:


# вычисление матрицы Якоби векторной функции y по вектору x
def jacobian(y, x):
    loop_vars = [
        tf.constant(0, tf.int32),
        tf.TensorArray(tf.float64, size=m),
    ]
    # конструируем цикл-подграф потока данных
    # в результате получим массив градиентов
    _, jacobian = tf.while_loop(
        lambda i, _: i < m,
        # каждый раз после вычисления градиента нам надо преобразовать его в 
        # одномерный терзор (вектор-строку), так как x может быть любой формы
        lambda i, res: (i+1, res.write(i, tf.reshape(tf.gradients(y[i], x), (-1,)))),
        loop_vars)
    # объединяем все градиенты в матрицу Якоби
    return jacobian.stack()

# вектор невязок из столбца в строку
r_flat = tf.squeeze(r)
# для каждого тензора параметров вычисляем матрицу Якоби
# потом эти матрицы объединяем в одну 
parms = [W1, b1, W2, b2]
parms_sizes = [tf.size(p) for p in parms]
j = tf.concat([jacobian(r_flat, p) for p in parms], 1)
jT = tf.transpose(j)
# матрица Якоби нам нужна для аппроксимации матрицы Гессе и градиента
hess_approx = tf.matmul(jT, j)
grad_approx = tf.matmul(jT, r)

Надо вычислить $\boldsymbol{J}r_{p}$ матрицу Якоби функции невязок по вектору параметров. Но у нас нет единого вектора параметров, а есть 4 тензора $W_1, b_1, W_2, b_2$. Считаем 4 матрицы $\boldsymbol{J}r_{W_1}, \boldsymbol{J}r_{b_1}, \boldsymbol{J}r_{W_2}, \boldsymbol{J}r_{b_2}$ и объединяем в одну функцией tf.concat.


Матрица Якоби состоит из градиентов каждого компонента функции невязок. tf.while_loop организует подграф потока данных, который пробегает по каждому компоненту $r_i$, вычисляет градиент и складывает его в массив тензоров, который потом объединяется в матрицу методом stack.


Градиент компонента $r_i$ по тензору $W_1$ выглядит так: $\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} \\ \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$. Функцией tf.reshape с параметром (-1,) он разворачивается в строку $\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} & \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$.


Такое вычисление матрицы Якоби требует много дополнительных действий. Эффективней было бы сначала все параметры объединить в один длинный вектор-строку и считать матрицу по нему. Так сделать нельзя — TensorFlow для вычисления градиента требует маршрут в графе потока данных от параметра к функции. Другое решение — завести тензор-переменную в виде длинного вектора-строки и из него сконструировать $W_1, b_1, W_2, b_2$. Тогда функция невязок будет зависеть от этого вектора-строки. Решение можно посмотреть здесь Levenberg-Marquardt Jupyter Notebook и здесь rosenbrock_train.py. Но даже такая реализация не очень быстрая, и зачастую TensorFlow считает реальную матрицу Гессе быстрее её аппроксимации. Если кто-то знает, как вычислить матрицу Якоби значительно (в разы) быстрее, пожалуйста, подскажите.


Обучим нейросеть методом Гаусса-Ньютона


Имея hess_approx и grad_approx можно запустить обучение нейронной сети методом Гаусса-Ньютона. Единственное отличие от оптимизации модели $rosenbrock$ заключается в том, что у нас вместо одного вектора параметров есть несколько тензоров параметров разной формы и размера. Нужны дополнительные действия:


  1. Вычислим изменения всех параметров: $\Delta \boldsymbol{p} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} & \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} & \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} & \Delta b_2\end{bmatrix}$
  2. Разобьём на отдельные части по размеру тензоров параметров:
    $\Delta W_{1} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$, $\Delta b_{1} = \begin{bmatrix} \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} \end{bmatrix}$, $\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} \end{bmatrix}$, $\Delta b_{2} = \begin{bmatrix} \Delta b_2\end{bmatrix}$.
  3. Изменим их форму, чтобы она соответствовала форме тензоров параметров:
    $\Delta W_{1} = \begin{bmatrix} \Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{1,10} \\ \Delta w^{(1)}_{2,1} &\cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$, $\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} \\ \vdots \\ \Delta w^{(2)}_{1,10} \\ \end{bmatrix}$
  4. Применим изменения.

# 1. насколько надо изменить параметры
dp_flat = tf.matmul(tf.linalg.inv(hess_approx), grad_approx)
# 2. разобьём изменения по тензорам
dps = tf.split(dp_flat, parms_sizes, 0)
# 3. приведём к соответствующей форме
for i in range(len(dps)):
    dps[i] = tf.reshape(dps[i], parms[i].shape)
# 4. шаг оптимизации: применяем тензоры изменений к тензорам параметров
gn = opt.apply_gradients(zip(dps, parms))
# запускаем оптимизацию
session.run(tf.global_variables_initializer())
train(1e-10, 100, loss, gn, feed_dict)

[Out]: step: 1, current loss: 548.8468777701685
       step: 2, current loss: 49648941.340197295
       InvalidArgumentError: Input is not invertible.

Что-то пошло не так. Сначала значение функции потерь резко выросло, а потом вообще всё сломалось с исключением. Метод Гаусса-Ньютона работает плохо, когда параметры очень далеки от оптимальных.


На этом шаге нас постигла неудача, но мы всё сделанное пригодится в следующем разделе.


Обучим нейросеть методом Левенберга-Марквадта


Подошли непосредственно к теме статьи. Самое понятное и полное описание алгоритма находится на портале Matlab руководство по функции trainlm. Все остальные статьи пытаются запутать неподготовленного читателя. Будем придерживаться терминологии компании MathWorks.


Мы записывали алгоритм Гаусса-Ньютона так: $\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$. Метод Леверберга-Марквадта отличается одной маленькой деталью:


$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}+\mu \boldsymbol{I}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$


Скалярная переменная $\mu$ умножается на диагональную единичную матрицу $I$ размерности $n$ (общее число параметров). Если число $\mu$ равно нулю, то шаг полностью совпадает с шагом Гаусса-Ньютона. Если число большое, то получаем градиентный спуск. Можно сказать, что LM колеблется между градиентным спуском и алгоритмом Гаусса-Ньютона.


Код практически совпадает с кодом из предыдущей части:


mu = tf.placeholder(tf.float64, shape=[1])
n = tf.add_n(parms_sizes)
I = tf.eye(n, dtype=tf.float64)
# 1. насколько надо изменить параметры
dp_flat = tf.matmul(tf.linalg.inv(hess_approx + tf.multiply(mu, I)), grad_approx)
# 2. разобьём изменения по тензорам
dps = tf.split(dp_flat, parms_sizes, 0)
# 3. приведём к соответствующей форме
for i in range(len(dps)):
    dps[i] = tf.reshape(dps[i], parms[i].shape)
# 4. шаг оптимизации: применяем тензоры изменений к тензорам параметров
lm = opt.apply_gradients(zip(dps, parms))

Как же вычислить подходящее значение $\mu$? Алгоритм LM стремится перейти к методу Гаусса-Ньютона как можно быстрее. Если не получается, то переходит к градиентному спуску. Фактически, после каждого удачного шага оптимизации $\mu$ уменьшается, а после каждой неудачи увеличивается. Ещё одна особенность алгоритма — производятся только шаги, которые действительно уменьшают значение mse. С деталями алгоритма проще разобраться по коду, он довольно простой:


# переменные для хранения предыдущих значений параметров
store = [tf.Variable(tf.zeros(p.shape, dtype=tf.float64)) for p in parms]
# операции TensorFlow для сохранения и откатывания значений параметров
save_parms = [tf.assign(s, p) for s, p in zip(store, parms)]
restore_parms = [tf.assign(p, s) for s, p in zip(store, parms)]

# пусть значение mu вначале будет равно 3.
feed_dict[mu] = np.array([3.])
step = 0
session.run(tf.global_variables_initializer())
# считаем начальное значение mse
current_loss = session.run(loss, feed_dict)
# сделаем не больше 100 шагов оптимизации
while current_loss > 1e-10 and step < 100:
    step += 1
    # логируем 1, 2, 4... шаг оптимизации
    if math.log(step, 2).is_integer():
        print(f'step: {step}, mu: {feed_dict[mu][0]} current loss: {current_loss}')
    # сохраняем значения параметров
    session.run(save_parms)
    # выполняем, пока не добьёмся уменьшения mse
    while True:
        # делаем шаг оптимизации
        session.run(lm, feed_dict)
        new_loss = session.run(loss, feed_dict)
        if new_loss > current_loss:
            # неудача - увеличиваем mu в 10 раз и восстанавливаем параметры
            feed_dict[mu] *= 10
            session.run(restore_parms)
        else:
            # удача - уменьшаем mu в 10 раз и движемся дальше
            feed_dict[mu] /= 10
            current_loss = new_loss
            break

print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}')
print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict)))

[Out]: step: 1, mu: 3.0 current loss: 692.6211687622557
       [...]
       ENDED ON STEP: 100, FINAL LOSS: 0.012346989371823602
       VALIDATION LOSS: 0.01859463694102034

За 100 шагов LM получили mse более чем в 10 раз меньше, чем за 40К шагов Адама.


Магические константы в реализации можно сделать настраиваемыми. Также можно заметить, что при каждой неудаче происходит полный пересчёт матрицы Якоби. Это неэффективно, более эффективный вариант реализации можно посмотреть здесь rosenbrock_train.py.


Познакомимся с многомерным вариантом функции Розенброка


Мы работали с 2D вариантом функции Розенброка. Работающая нейронная сеть для таких случаев не очень впечатляет. Интереснее становится с возрастанием числа измерений. В многомерном случае мы не можем достаточно плотно заполнить пространство, и нас начинает преследовать "проклятие размерности" (curse of dimentionality, Bellman, 1961). Интересная статья про многомерность Теория счастья. Закон арбузной корки и нормальность ненормальности.


Многомерный вариант функции Розенброка выглядит так:


$f(\boldsymbol{x}) = \sum_{i=1}^{N-1}\left [ 100(x_{i+1} - x_{i}^2)^2 + (1-x_{i})^2 \right ], \boldsymbol{x}=[x_1 \cdots x_{N}]\in \mathbb{R}^N$


Реализация есть здесь rosenbrock_train.py в функции get_rand_rosenbrock_points.


Полноценно проверим алгоритм Левенберга-Марквадта


Всю статью мы делали как-то так: "Вау! Алгоритм справился за 4 шага, а градиентный спуск за 300!". На самом деле, число шагов (эпох) интересует только редких математиков-теоретиков. Нас, инженеров, интересует время. Шаг Левенберга-Марквадта дороже шага Адама. Намного дороже. Что выгоднее: сделать много дешёвых шагов или мало дорогих? Надо заметить, что мы решали очень простую задачу на малом объёме данных. Так себе тест. Реально сложную задачу решать на своём домашнем компьютере не хотелось, но тест средней серьёзности я всё-таки провёл:


  1. 10 000 точек 6D функции Розенброка.
  2. Многослойный перцепторн с 3 слоями шириной 12, 10, 8 (311 параметров).
  3. Масштабирование входных данных.
  4. 3.5 часа работы каждого алгоритма.

Оптимизаторы работали на одних и тех же тренировочных данных и начинали с одинаковых параметров. Градиентный спуск побеждал алгоритм Левенберга-Марквадта в течение 2 часов. Потом для интереса запустил вариант LM с настоящей матрицей Гессе и настоящим градиентом. Он победил градиентный спуск за 20 минут.



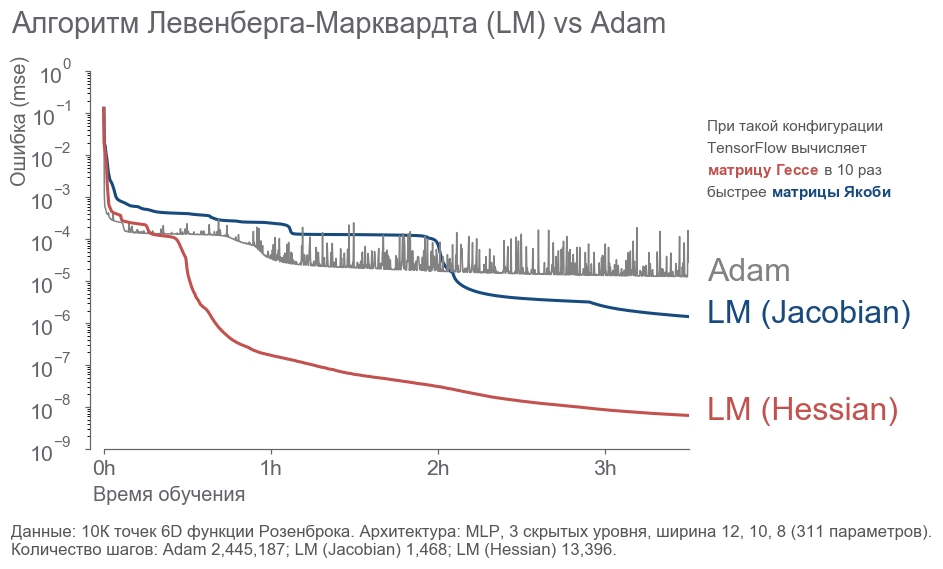
Код теста здесь rosenbrock_train.py. Это консольное приложение. Через параметры можно настраивать объём и размерность входных данных, структуру нейронной сети и свойства оптимизаторов.


Заключение


Как оказалось, я могу писать статьи только методом градиентного спуска. Сначала "набрасываю лопатой", потом сотни раз прочитываю, вношу небольшие дополнения и правки. Наверняка результат получился далёкий от оптимального, и осталось много неточностей и ошибок. Но я старался, а счётчик показывает 273 шага. Если что-то непонятно, то буду рад ответить на вопросы и помочь.


Хотелось бы реализовать, но не успел:


  1. Быстрое вычисление матрицы Якоби.
  2. Умножение больших матриц (Якоби саму на себя) методом Монте-Карло:
    [1] Petros Drineas, Ravi Kannan, and Michael W. Mahoney. 2006. Fast Monte Carlo Algorithms for Matrices I: Approximating Matrix Multiplication. SIAM J. Comput. 36, 1 (July 2006), 132-157. DOI=http://dx.doi.org/10.1137/S0097539704442684
    [2] Adelman, M., & Silberstein, M. (2018). Faster Neural Network Training with Approximate Tensor Operations. CoRR, abs/1805.08079.

Конечно, алгоритм Левенберга-Марквадта не подходит для всех ситуаций. Если количество параметров больше нескольких тысяч, то скорее всего он будет бесполезен. Но в некоторых ситуациях он "решает".

Tags:
Hubs:
+67
Comments15
29
Karma
0
Rating
Андрей Гаськов @AndreyGaskov

программист, аналитик данных

Send message

Articles

Show the best of all time
Unlock dark mode

Your account

Sections

Information

Services

Support
© 2006–2024, Habr