Одна из важных подзадач видеоаналитики — слежение за объектами на видео. Она не настолько примитивна, чтобы пришлось спускаться на попиксельный уровень, но и не настолько сложна, чтобы однозначно требовать для решения многослойную нейронную сеть. Трекинг может использоваться как самоцель, так и в составе других алгоритмов:
Даже не глядя в литературу, я могу с уверенностью сказать, что наилучший способ решить поставленную задачу — использовать нейронные сети. В общем-то, дальше можно было бы ничего и не писать, но не всегда в задачу можно кинуться парой GTX 1080Ti. Кому интересно, как отслеживают объекты на видео в таких случаях, прошу под кат. Я попробую не просто объяснить, как работают ASEF и MOSSE трекеры, а подвести вас к решению, чтобы формулы показались очевидными.
Для начала ответим на предварительный вопрос: зачем что-то изобретать, когда можно скормить tensorflow пачку видео и отойти от компьютера на пару недель? У нейросетевых подходов есть один серьёзный недостаток: даже на современных видеокартах сложно добиться от сетей хорошей скорострельности. Это не проблема, если мы анализируем записанное видео, но вставляет палку в колёса, если хочется работать в реальном времени. Допустим, мы хотим обрабатывать видео с пяти камер в 10 FPS. Даже с такими сравнительно мягкими условиями нейронная сеть должна иметь inference time меньше чем миллисекнуд (в условиях полной непараллельности). Для сравнения, YoloV3, сеть-классификатор со сравнительно простой архитектурой, может выплёвывать по картинке в
миллисекнуд (в условиях полной непараллельности). Для сравнения, YoloV3, сеть-классификатор со сравнительно простой архитектурой, может выплёвывать по картинке в  миллисекунд. Кроме того, решения на базе мощных видеокарт могут быть банально дороги.
миллисекунд. Кроме того, решения на базе мощных видеокарт могут быть банально дороги.
Эта статья предполагает, что вы уже имели дело с машинной обработкой изображений, знакомы с базовыми операциями линейной алгебры (свёртка, норма, обращение матриц) и в общих чертах понимаете преобразование Фурье.
Здесь и далее:
На первый взгляд задача отслеживать определённый предмет не кажется такой уж сложной.
Пусть у нас есть последовательных кадров видео
последовательных кадров видео  размера
размера  на
на  пикселей. На начальном кадре видео
пикселей. На начальном кадре видео  вокруг некоторого объекта обведён прямоугольник
вокруг некоторого объекта обведён прямоугольник 
 на
на  . Требуется найти местоположение этого тела на всех остальных кадрах
. Требуется найти местоположение этого тела на всех остальных кадрах  .
.
Уберём шум на изображениях, затем нормируем каждое из них в диапазон от -1 до 1, чтобы общие изменения яркости не влияли на детекции. Возьмём первый кадр видео без разметки . Если
. Если  и
и  — соседние кадры видео с хорошим FPS, то вряд ли искомый объект далеко удалился от исходного положения. Воспользуемся этим. Вырежем из
— соседние кадры видео с хорошим FPS, то вряд ли искомый объект далеко удалился от исходного положения. Воспользуемся этим. Вырежем из  прямоугольник
прямоугольник  с места, где раньше находилось искомое тело. «Протащим»
с места, где раньше находилось искомое тело. «Протащим»  сквозь
сквозь  и в каждой точке посчитаем квадрат суммы разностей
и в каждой точке посчитаем квадрат суммы разностей  нужно совместить центр
нужно совместить центр  с элементом
с элементом  в
в  , а отсутствующие значения занулить. После этого в матрице
, а отсутствующие значения занулить. После этого в матрице  ищется минимум; его местоположение минус координаты центра
ищется минимум; его местоположение минус координаты центра  и будет смещением искомого объекта на
и будет смещением искомого объекта на  .
.
Чтобы резкий переход в ноль не «звенел» при детекции, лучше изначально взять прямоугольник чуть больше, чем надо и плавно сводить к нулю значения ближе к границам и
и  . Для этого каждый из
. Для этого каждый из  нужно умножить на маску. В случае квадратных объектов подойдёт старая добрая экспонента
нужно умножить на маску. В случае квадратных объектов подойдёт старая добрая экспонента  (где
(где  — центр окна), но в общем случае лучше взять двумерное окно Хеннинга.
— центр окна), но в общем случае лучше взять двумерное окно Хеннинга.
Для окно
окно  берётся с позиции, предсказанной на кадре
берётся с позиции, предсказанной на кадре  , и так далее.
, и так далее.
Вместо нормы можно использовать
нормы можно использовать  (
( ) и минус кросс-корреляцию матриц (
) и минус кросс-корреляцию матриц (![$G_{nCC}(i, j) = -\sum_{kl}{F_{1,kl}(i,j)F_{0,kl}}, k \in [0, m], l \in [0, n] $](https://habrastorage.org/getpro/habr/formulas/62d/834/c1b/62d834c1b474ac75ebc5beb555d800d1.svg) ). И то и другое считается немного быстрее, чем
). И то и другое считается немного быстрее, чем  , но у них есть свои особенности.
, но у них есть свои особенности.  недифференцируема и менее чувствительна к большим отличиям в значениях пикселей. Кросс-корреляция может давать ложные срабатывания, если образец низкоконтрастный, и на изображении есть очень светлые или очень тёмные участки.
недифференцируема и менее чувствительна к большим отличиям в значениях пикселей. Кросс-корреляция может давать ложные срабатывания, если образец низкоконтрастный, и на изображении есть очень светлые или очень тёмные участки.
 -версия метрики не имеет такого недостатка:
-версия метрики не имеет такого недостатка:  , «энергия» выбранного участка на
, «энергия» выбранного участка на  выступает в качестве уравновешивающего фактора (
выступает в качестве уравновешивающего фактора ( , сумма квадратов значений пикселей образца, одинакова для всех положений окна и не имеет здесь практической значимости).
, сумма квадратов значений пикселей образца, одинакова для всех положений окна и не имеет здесь практической значимости).
Даже такой примитивный алгоритм довольно неплохо справляется в случае линейного движения объектов (например, камера, смотрящая сверху вниз на конвейер). Однако из-за простоты модели и исполнения у такого способа слежения есть несколько недостатков:
Закатаем рукава и попробуем решить вышеобозначенные проблемы.
Аугменитруем исходное изображение. Применим к нему несколько несильных аффинных трансформаций. Также можно добавить шум или изменить гамму. Таким образом вместо одного изображения получается микродатасет из картинок. Изображений стало много, а окно осталось одно. Значит теперь будем не просто вырезать прямоугольник с изображения, а искать некоторый фильтр
картинок. Изображений стало много, а окно осталось одно. Значит теперь будем не просто вырезать прямоугольник с изображения, а искать некоторый фильтр  , который будет давать давал хороший отклик для каждого
, который будет давать давал хороший отклик для каждого  . Преобразуем проблему в задачу минимизации:
. Преобразуем проблему в задачу минимизации:  — сумма квадратов попиксельных разностей между
— сумма квадратов попиксельных разностей между  и соответствующим ему участку точного местоположения объекта на
и соответствующим ему участку точного местоположения объекта на  -том синтетическом изображении, созданном из кадра, на котором есть истинная разметка.
-том синтетическом изображении, созданном из кадра, на котором есть истинная разметка.
Кроме этого можно насэмплировать прямоугольников вдалеке от местоположения отслеживаемого объекта и максимизировать на них разность, показанную выше.
С предложением, чтобы фильтр давал хороший отклик в точках рядом с точным местоположением объекта сложнее. Мы знаем что в применение фильтра с
применение фильтра с  -метрикой должно давать 0, рядом — больше, далеко — ещё больше. Причём, у нас нет какого-то предпочитаемого направления, отклик должен быть центрально симметричен относительно
-метрикой должно давать 0, рядом — больше, далеко — ещё больше. Причём, у нас нет какого-то предпочитаемого направления, отклик должен быть центрально симметричен относительно  . Выглядит так, будто мы можем математически выразить, как должен выглядеть отклик фильтра, применённого к опорным изображениям! Точный вид может разниться в зависимости от конкретной функции затухания отклика, но ведь все любят гауссианы? Значит, положим, что
. Выглядит так, будто мы можем математически выразить, как должен выглядеть отклик фильтра, применённого к опорным изображениям! Точный вид может разниться в зависимости от конкретной функции затухания отклика, но ведь все любят гауссианы? Значит, положим, что  , применённый к
, применённый к  в идеальном случае должен давать результат
в идеальном случае должен давать результат  . Следовательно, задача минимизации превращается в:
. Следовательно, задача минимизации превращается в:
Секундочку… У нас получилось уравнений с
уравнений с  переменными для минимизации. Кажется, мы перестарались. Вернёмся немного назад.
переменными для минимизации. Кажется, мы перестарались. Вернёмся немного назад.
Из всех проблем наибольшие затруднения вызывает сложность . Разве можно тут что-то придумать кроме хитрого разбиение одного окна поиска на несколько маленьких или поиска на картинке в маленьком разрешении и подстройки на высокоточной?
. Разве можно тут что-то придумать кроме хитрого разбиение одного окна поиска на несколько маленьких или поиска на картинке в маленьком разрешении и подстройки на высокоточной?
Оказывается, можно! Матанализ говорит нам, что свёртка функций в обычном пространстве — это перемножение их Фурье-образов. Применять быстрое преобразование Фурье к изображениям, умножать их частоты поэлементно, а затем превращать результат обратно в матрицу мы умеем за , что гораздо быстрее, чем сворачивать матрицы по-честному. Фурье! Кто бы мог подумать! В век tensorflow он всё ещё может помочь нам в компьютерном зрении.
, что гораздо быстрее, чем сворачивать матрицы по-честному. Фурье! Кто бы мог подумать! В век tensorflow он всё ещё может помочь нам в компьютерном зрении.
(Это, кстати, демонстрирует общий математический принцип: если не хочешь решать задачу в пространстве , перенеси её в пространство
, перенеси её в пространство  , реши там, и перенеси решение обратно. Обходной путь часто оказывается короче прямого.)
, реши там, и перенеси решение обратно. Обходной путь часто оказывается короче прямого.)
Как было показано выше, мы можем использовать для локализации образца на изображении кросс-корреляцию. Но кросс-корреляция — это свёртка с горизонтально и вертикально отражённым . Матанализ подсказывает, что в этом случае нужно будет умножить частоты
. Матанализ подсказывает, что в этом случае нужно будет умножить частоты  на комплексно-сопряжённую матрицу к матрице частот
на комплексно-сопряжённую матрицу к матрице частот  :
:
 — функция идеального отклика на опорном изображении. Обратите внимание, что
— функция идеального отклика на опорном изображении. Обратите внимание, что  -метрику мы минимизировали, а свёрточную — максимизируем, так что теперь, чем больше отклик, тем лучше.
-метрику мы минимизировали, а свёрточную — максимизируем, так что теперь, чем больше отклик, тем лучше.
Будь у нас одно изображение, то мы бы найти точную матрицу частот фильтра: изображений из исходного. Мы можем применить их и с Фурье-подходом. Нет фильтра с такими частотами, которые бы идеально удовлетворяли бы всем изображениям, но можно получить что-то достаточно хорошее. Есть два способа, которыми можно решить проблему:
изображений из исходного. Мы можем применить их и с Фурье-подходом. Нет фильтра с такими частотами, которые бы идеально удовлетворяли бы всем изображениям, но можно получить что-то достаточно хорошее. Есть два способа, которыми можно решить проблему:
Хм, как будто бы в формулах участвуют похожие элементы. При формулы для ASEF и MOSSE и вовсе совпадают.
формулы для ASEF и MOSSE и вовсе совпадают.  для одного изображения можно представить как
для одного изображения можно представить как
После того как мы получили , мы вычисляем отклик в частотной области
, мы вычисляем отклик в частотной области  , затем переводим его в пространственную область и ищем максимум в получившейся матрице
, затем переводим его в пространственную область и ищем максимум в получившейся матрице  . Где максимум — там и новое положение объекта.
. Где максимум — там и новое положение объекта.
Соберём всё вместе.
Общее состояние:
Матрица частот фильтра:
Вспомогательные матрицы для вычисления частот фильтра:
Матрица частот желаемого идеального отклика:
Скорость обучения во время трекинга:
Прямоугольник текущего положения объекта:
Количество трансформаций:
Порог отклика:
Вспомогательная функция: Тренировка. Вход: изображение , текущая скорость обучения
, текущая скорость обучения 
Инициализация. Вход: изображение , прямоугольник вокруг положения объекта
, прямоугольник вокруг положения объекта 
Трекинг: Вход: изображение
Подробности имплементации могут варьироваться. Например,
Для начала, несколько примеров двумерного Фурье-преобразования.
Теперь перейдём к реальному примеру работы:
Тот же пример с более узким желаемым откликом:
 для предыдущих трёх случаев
для предыдущих трёх случаев  при использовании для обучения 16 трансформаций входного изображения:
при использовании для обучения 16 трансформаций входного изображения:
Если вы хотите увидеть, как это выглядит вживую, скачайте отсюда мой тестовый репозиторий с имплементацией MOSSE с выводом отладочных картинок. На гитхабе можно найти больше вариантов MOSSE. Кроме того, он есть в OpenCV.
Спасибо за внимание, хабровчане. MOSSE и ASEF трекинг — не самые сложные алгоритмы на свете. Тем легче не только их эффективно применить, но и и понять, чем руководствовались их создатели. Я надеюсь, что моё объяснение помогло вам проникнуть в голову исследователей, проследить за ходом их мысли. Это может оказаться полезным: машинное обучение — не статическая область знаний, в ней есть место для творчество и собственных исследований. Попробуйте поковыряться в каком-нибудь устоявшемся алгоритме: поотпиливать ненужные конечности для ускорения или добавить парочку, чтобы он стал работать лучше в вашем частном случае. Вам понравится!
Статья написана при поддержке компании DSSL.
- Подсчёт уникальных людей, зашедших в определённую зону или перешедших через границу в кадре
- Определение типичных маршрутов машин на стоянке и людей в магазине
- Автоматический поворот камеры видеонаблюдения при смещении объекта
Даже не глядя в литературу, я могу с уверенностью сказать, что наилучший способ решить поставленную задачу — использовать нейронные сети. В общем-то, дальше можно было бы ничего и не писать, но не всегда в задачу можно кинуться парой GTX 1080Ti. Кому интересно, как отслеживают объекты на видео в таких случаях, прошу под кат. Я попробую не просто объяснить, как работают ASEF и MOSSE трекеры, а подвести вас к решению, чтобы формулы показались очевидными.
Для начала ответим на предварительный вопрос: зачем что-то изобретать, когда можно скормить tensorflow пачку видео и отойти от компьютера на пару недель? У нейросетевых подходов есть один серьёзный недостаток: даже на современных видеокартах сложно добиться от сетей хорошей скорострельности. Это не проблема, если мы анализируем записанное видео, но вставляет палку в колёса, если хочется работать в реальном времени. Допустим, мы хотим обрабатывать видео с пяти камер в 10 FPS. Даже с такими сравнительно мягкими условиями нейронная сеть должна иметь inference time меньше чем
Эта статья предполагает, что вы уже имели дело с машинной обработкой изображений, знакомы с базовыми операциями линейной алгебры (свёртка, норма, обращение матриц) и в общих чертах понимаете преобразование Фурье.
Здесь и далее:
обозначает поэлементное умножение матриц
и
обозначает свёртку матриц
и
обозначает что
— матрица частот быстрого преобразования Фурье, применённого к изображению
.
— обозначает сумму квадратов элементов матрицы
Тривиальное решение
На первый взгляд задача отслеживать определённый предмет не кажется такой уж сложной.
Пусть у нас есть
Уберём шум на изображениях, затем нормируем каждое из них в диапазон от -1 до 1, чтобы общие изменения яркости не влияли на детекции. Возьмём первый кадр видео без разметки
Чтобы резкий переход в ноль не «звенел» при детекции, лучше изначально взять прямоугольник чуть больше, чем надо и плавно сводить к нулю значения ближе к границам
Для
Пример

Вместо
Даже такой примитивный алгоритм довольно неплохо справляется в случае линейного движения объектов (например, камера, смотрящая сверху вниз на конвейер). Однако из-за простоты модели и исполнения у такого способа слежения есть несколько недостатков:
- Простое линейное движение объекта без изменений в природе встречается нечасто. Как правило тела в поле зрения камеры могут претерпевать некоторые классы изменений. В порядке увеличения сложности: увеличение/уменьшения размера, повороты, аффинные преобразования, проективные преобразования, нелинейные преобразования, изменения объекта. Даже если опустить изменения объекта и нелинейные преобразования, хотелось бы, чтобы алгоритм мог бы восстанавливаться после сравнительно простых поворотов и изменений размера. Очевидно, что вышеописанная процедура таким свойством не обладает. Вероятно,
всё равно даст заметный отклик на объекте, но будет сложно определить точное местоположение образца, и трек будет прерывистым.
Пример
- Мы показали алгоритму только один положительный образец, сложно сказать, какой отклик даст
, если в окно попадёт другой похожий объект. Хорошо, если искомый объект контрастный и имеет редко встречающуюся структуру, но что если мы хотим следить за машиной в потоке других машин? Трекер может непредсказуемо перепрыгивать с одного автомобиля на другой.
- На каждом кадре мы отбрасываем всю предысторию. Наверное, её тоже следует как-то использовать.
- Более того, мы обучаемся только на одной точке изображения. Будет лучше, если вблизи правильного местоположения объекта трекер тоже будет давать хороший отклик. Немного контринтуитивно, но подумайте: если фильтр в точном местоположении объекта на картинке
даёт наилучшее значение, а в
— какое-то случайное, значит, он слишком чувствителен к мелким деталям, которые могут легко измениться. И наоборот, если в
и в
примерно одинаковые хорошие значения, то фильтр «зацепился» за более крупные и, как мы надеемся, более постоянные признаки.
- При наивной реализации отслеживающей процедуры мы для каждого пикселя кадра умножаем всё окно с выбранным предметом на соответствующую часть этого кадра. Сложность этой операции —
. В таких случаях не очень приятно отслеживать даже объекты 50 на 50 пикселей. Эта проблема частично решается уменьшением размера видео, но при уменьшении картинки меньше 240 пикселей по ширине начинают теряться даже крупные значимые детали, что лишает алгоритм смысла.
ASEF, MOSSE
Тривиальный подход++?
Закатаем рукава и попробуем решить вышеобозначенные проблемы.
Аугменитруем исходное изображение. Применим к нему несколько несильных аффинных трансформаций. Также можно добавить шум или изменить гамму. Таким образом вместо одного изображения получается микродатасет из
Кроме этого можно насэмплировать прямоугольников вдалеке от местоположения отслеживаемого объекта и максимизировать на них разность, показанную выше.
С предложением, чтобы фильтр давал хороший отклик в точках рядом с точным местоположением объекта сложнее. Мы знаем что в
Секундочку… У нас получилось
Основной приём
Из всех проблем наибольшие затруднения вызывает сложность
Оказывается, можно! Матанализ говорит нам, что свёртка функций в обычном пространстве — это перемножение их Фурье-образов. Применять быстрое преобразование Фурье к изображениям, умножать их частоты поэлементно, а затем превращать результат обратно в матрицу мы умеем за
(Это, кстати, демонстрирует общий математический принцип: если не хочешь решать задачу в пространстве
Как было показано выше, мы можем использовать для локализации образца на изображении кросс-корреляцию. Но кросс-корреляция — это свёртка с горизонтально и вертикально отражённым
Будь у нас одно изображение, то мы бы найти точную матрицу частот фильтра:
- Можно найти набор идеальных фильтров, а потом усреднить их в один. Таким путём идут авторы работы Average of Synthetic Exact Filters (ASEF):
Здесь мы пользуемся свойством линейности Фурье-образов. Складывая частоты, как показано выше, мы как будто усредняем несколько весов фильтров. - Можно найти частоты фильтра, которые удовлетворяют всем картинкам в среднем, примерно как для
:
Чтобы найти минимум, нужно взять производную по элементам фильтра:
Честное взятие этой производной можно посмотреть в работе Visual Object Tracking using Adaptive Correlation Filters, которая предлагает фильтры Minimum Output Sum of Squared Error (MOSSE-фильтры). Результат получится такой:
Хм, как будто бы в формулах участвуют похожие элементы. При
После того как мы получили
Дополнительные моменты
- Члены суммы в знаменателях формул имеют интересный физический смысл.
— это энергетический спектр прямоугольника с
-того изображения.
- Обратите внимание на интересную симметрию. Нужно было умножить частоты фильтра на частоты изображения, чтобы получить отклик. Теперь нужно умножить частоты отклика на частоты изображения (и нормализовать), чтобы получились частоты фильтра.
- В реальной жизни при поэлементном делении может возникнуть деление на ноль, так что в знаменатель обычно добавляют регуляризующую константу
. Утверждается, что такая регуляризация заставляет фильтр больше обращать внимание на низкие частоты, что улучшает обобщающую способность.
- При обработке реального видео обычно хочется сохранять информацию об отслеживаемом объекте, полученную с предыдущих кадров. При переходе на следующий кадр можно не вычислять
с нуля, а обновить предыдущий. Формула обновления для ASEF:
Для MOSSE нужно накапливать числитель и знаменатель отдельно:
где— скорость обучения.
- Важно помнить, что преобразование Фурье — не совсем то же самое, что и вычисление
по-честному, как описано в начале статьи. При вычисление БПФ отсутствующие элементы не зануляются, а подставляются с обратной стороны, как если бы изображение зацикливалось справа-налево и снизу-вверх. Но в самом начале статьи мы уже решили затемнять края
, так что эта проблема не окажет заметного влияния.
- Как упомянуто выше, кросс-корреляция имеет неприятную особенность: в целом светлый фильтр может давать сильный отклик на белых областях изображения, даже если они не совпадают в контрастных участках. Этим проблемы не ограничиваются. Даже один совпадающий пиксель с сильноположительным или сильноотрицательным значением может внести помехи в работу фильтра, если образец в целом низкоконтрастный. Чтобы сгладить этот эффект, в препроцессинг нужно включить нелинейное преобразование пикселей изображения, которое «прижмёт» слишком светлые и слишком тёмные участки к среднему. Благодаря этому совпадение настоящих контрастных участков вносит более сильный вклад в метрику. В статьях ASEF и MOSSE используется логарифм:
где пикселиот 0 до 255. На мой взгляд, это слишком жёстко, и игнорирует проблему сильного отклика тёмного фильтра на чёрных участках. Лучше работает такая схема:
После чего идёт нормализация, и оказывается, что большинство элементов сосредоточены вокруг нуля.
- Как при таком алгоритме определить, что отслеживаемый объект пропал с кадра? Здесь поможет более детальный анализ отклика, полученного с очередного кадра. Создатели MOSSE предлагают показатель PSR — Peak to Sidelobe Ratio. Пусть
— максимальный элемент
, соответствующий новому положению объекта
. Исключим из рассмотрения квадрат
вокруг этого максимума. Посчитаем по остальным пикселям среднее и среднеквадратчное отклонение (
). Тогда
Если это значение выше определённого порога, то детекция считается удачной. Порог обычно берётся в районе между 3 и 10. Для уверенных детекций PSR обычно держится выше 20.
(заметьте, что здесь PSR означает совсем не то, что он обычно означает в теории обработки сигналов; так что не гуглите его применение, ничего хорошего не выйдет) - Алгоритм чрезвычайно прост. Выполнение процедуры трекинга на Core-i7 на картинках с 320x400 при использовании OpenCV-имплементации занимает от 0.5 до 2 миллисекунд в зависимости от размера отслеживаемого объекта.
Алгоритм MOSSE
Соберём всё вместе.
Общее состояние:
Матрица частот фильтра:
Вспомогательные матрицы для вычисления частот фильтра:
Матрица частот желаемого идеального отклика:
Скорость обучения во время трекинга:
Прямоугольник текущего положения объекта:
Количество трансформаций:
Порог отклика:
Вспомогательная функция: Тренировка. Вход: изображение
- Пока не набралось
трансформаций:
- Применить к изображению небольшую случайную аффинную трансформацию с центром в центре
- Вырезать из изображения с прямоугольник с объектом
- Применить к нему маску, чтобы плавно занулить края
- Перевести
в частотную область:
- Применить к изображению небольшую случайную аффинную трансформацию с центром в центре
- Если
, то заменить
и
на
и
. Иначе:
- Вычислить частоты фильтра:
Инициализация. Вход: изображение
- Приготовить желаемый отклик
. Обычно это полностью занулённая матрица с небольшой гауссианой в центре.
- Тренировка:
, 1.0
- Перевести
в частотную область:
Трекинг: Вход: изображение
- Вырезать прямоугольник
из
для имеющегося предыдущего положения объекта
- Применить к нему маску, чтобы плавно занулить края
- Перевести
в частотную область:
- Перевести
в пространственную область:
- Найти максимум в
:
- Посчитать силу отклика
- Если
, выйти с неудачей
- Обновить положение
. Подстроить R, если он вышел за пределы изображения, или было решено, что объект увеличился/уменьшился.
- Тренировка:
,
- Вернуть
Подробности имплементации могут варьироваться. Например,
- Препроцесситься может только
, а не всё изображение.
может пересоздаваться для каждой трансформации изображения с варьированием функции и ширины отклика.
- Можно одновременно обучать несколько различных фильтров на нескольких масштабах объекта, чтобы обнаруживать перемещения вдаль и вблизь.
Как это выглядит
Для начала, несколько примеров двумерного Фурье-преобразования.
Несколько простых примеров
Напомню, что результат преобразования комплекснозначный. На картинках ниже представлены группы «изображение — абсолютные значения частотной области в обычном масштабе — абсолютные значения частотной области в логарифмическом масштабе».
Вертикальные линии:



Картинка изменяется слева направо одинаково для любого положения по вертикали. Более того, изменение периодическое, с чётким периодом и явным паттерном. Поэтому на картинках частот вы видите только частоты вдоль оси .
.
Клетка:



Обратите внимание, что есть как ожидаемые серии частот вдоль осей и
и  , так и странные паразитные частоты. Они появились из-за того, что во-первых, картинка конечна, тогда как Фурье-образ разлагается в красивую сумму только для бесконечного периодического сигнала. Во-вторых, можно заметить, что изображение не образует точный период на краях.
, так и странные паразитные частоты. Они появились из-за того, что во-первых, картинка конечна, тогда как Фурье-образ разлагается в красивую сумму только для бесконечного периодического сигнала. Во-вторых, можно заметить, что изображение не образует точный период на краях.
Наклонные линии:



Снова видны как частоты, соответствующие основному направлению, так и паразитные частоты.
Наклонные линии плюс дисторсия:



На образе частот видно несколько характерных направлений, но интуитивно представить по ним картинку уже становится сложно.
Для изображений настоящего мира представить картинку в голове по её частотам ещё сложнее:



(частоты в центре закрыты, чтобы они не «засвечивали» остальной спектр)
Вертикальные линии:



Картинка изменяется слева направо одинаково для любого положения по вертикали. Более того, изменение периодическое, с чётким периодом и явным паттерном. Поэтому на картинках частот вы видите только частоты вдоль оси
Клетка:



Обратите внимание, что есть как ожидаемые серии частот вдоль осей
Наклонные линии:



Снова видны как частоты, соответствующие основному направлению, так и паразитные частоты.
Наклонные линии плюс дисторсия:



На образе частот видно несколько характерных направлений, но интуитивно представить по ним картинку уже становится сложно.
Для изображений настоящего мира представить картинку в голове по её частотам ещё сложнее:



(частоты в центре закрыты, чтобы они не «засвечивали» остальной спектр)
Теперь перейдём к реальному примеру работы:
Пачка картинок
Изображение с размеченным объектом:

Вырезанный и предобработанный объект, его спектр в обычном и логарифмическом масштабе ( ):
):



Желаемый отклик ( ):
):

Частоты фильтра в обычном и логарифмическом масштабе ( ):
):


Явно выраженные веса фильтра (без применения трансформаций ):
):

Обратите внимание, что они нигде не участвуют в алгоритме — их можно посчитать разве что ради интереса. Также обратите внимание, что фильтр выглядит как чёрте что. Можно было бы ожидать, что фильтром оказалось бы что-то похожее на изначальное изображение, но это отнюдь не всегда правда. Фильтр, похожий на само изображение вряд ли бы дал желаемую гауссиану откликом.
Отклик от следующего кадра:

Хоть он и не такой чистый, как желаемый отклик, на нём легко определить максимум.

Вырезанный и предобработанный объект, его спектр в обычном и логарифмическом масштабе (



Желаемый отклик (

Частоты фильтра в обычном и логарифмическом масштабе (


Явно выраженные веса фильтра (без применения трансформаций

Обратите внимание, что они нигде не участвуют в алгоритме — их можно посчитать разве что ради интереса. Также обратите внимание, что фильтр выглядит как чёрте что. Можно было бы ожидать, что фильтром оказалось бы что-то похожее на изначальное изображение, но это отнюдь не всегда правда. Фильтр, похожий на само изображение вряд ли бы дал желаемую гауссиану откликом.
Отклик от следующего кадра:

Хоть он и не такой чистый, как желаемый отклик, на нём легко определить максимум.
Тот же пример с более узким желаемым откликом:
Пачка картинок
Уже:

 :
:

Ещё уже:

 :
:
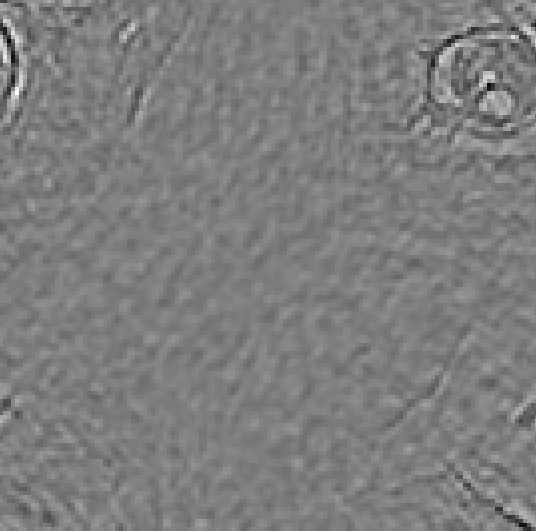
При очень узком максимуме на фильтре вместо чёрного пятна становится явно виден глаз.


Ещё уже:


При очень узком максимуме на фильтре вместо чёрного пятна становится явно виден глаз.
Ещё пачка картинок
Широкий максимум:

Средний максимум:
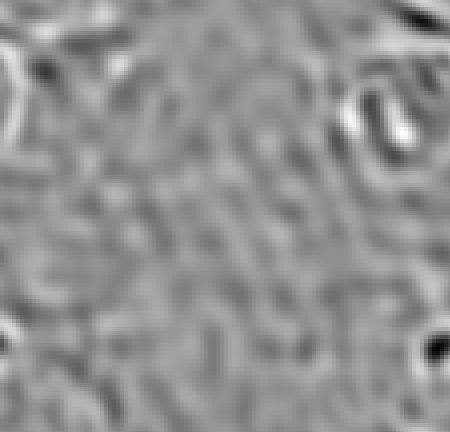
Узкий максимум:

Чем больше трансформаций, тем меньше фильтр цепляется за случайные элементы. Особенно хорошо видно, что пропали случайные чёрно-белые пятна из середины . С другой стороны, для узкой гауссианы обучение на нескольких картинках может сыграть в минус: посмотрите на «звон» образовавшийся в фильтре вокруг глаза.
. С другой стороны, для узкой гауссианы обучение на нескольких картинках может сыграть в минус: посмотрите на «звон» образовавшийся в фильтре вокруг глаза.

Средний максимум:

Узкий максимум:

Чем больше трансформаций, тем меньше фильтр цепляется за случайные элементы. Особенно хорошо видно, что пропали случайные чёрно-белые пятна из середины
Если вы хотите увидеть, как это выглядит вживую, скачайте отсюда мой тестовый репозиторий с имплементацией MOSSE с выводом отладочных картинок. На гитхабе можно найти больше вариантов MOSSE. Кроме того, он есть в OpenCV.
Заключение
Спасибо за внимание, хабровчане. MOSSE и ASEF трекинг — не самые сложные алгоритмы на свете. Тем легче не только их эффективно применить, но и и понять, чем руководствовались их создатели. Я надеюсь, что моё объяснение помогло вам проникнуть в голову исследователей, проследить за ходом их мысли. Это может оказаться полезным: машинное обучение — не статическая область знаний, в ней есть место для творчество и собственных исследований. Попробуйте поковыряться в каком-нибудь устоявшемся алгоритме: поотпиливать ненужные конечности для ускорения или добавить парочку, чтобы он стал работать лучше в вашем частном случае. Вам понравится!
Статья написана при поддержке компании DSSL.
