How to become an author
Search
Write a publication
Pull to refresh

Дротики, кости и монеты: алгоритмы выборки из дискретного распределения

Reading time45 min
Views9.1K
Algorithms*Mathematics*
Translation
Original author: Keith Schwarz

Однажды я задал на Stack Overflow вопрос о структуре данных для шулерских игральных костей. В частности, меня интересовал ответ на такой вопрос: «Если у нас есть n-гранная кость, у грани которой i есть вероятность выпадения pi. Какова наиболее эффективная структура данных для симуляции бросков такой кости?»

Такую структуру данных можно использовать для многих задач. Например, можно применять её для симуляции бросков честной шестигранной кости, присвоив вероятность $\frac{1}{6}$ каждой из сторон кости, или для симуляции честной монетки имитацией двусторонней кости, вероятность выпадения каждой из сторон которой равна $\frac{1}{2}$. Также можно использовать эту структуру данных для непосредственной симуляции суммы двух честных шестигранных костей, создав 11-гранную кость (с гранями 2, 3, 4, ..., 12), каждая грань которой имеет вес вероятности, соответствующий броскам двух честных костей. Однако можно также использовать эту структуру данных и для симуляции шулерских костей. Например, если вы играете в «крэпс» с костью, которая, как вы точно знаете, не идеально честная, то можно использовать эту структуру данных для симуляции множества бросков костей и анализа оптимальной стратегии. Также можно попробовать симулировать аналогичным образом неидеальное колесо рулетки.

Если выйти за пределы игр, то можно применить эту структуру данных в симуляции роботов, датчики которых имеют известные уровни отказа. Например, если датчик дальности имеет 95-процентную вероятность возврата правильного значения, 4-процентную вероятность слишком маленького значения, и 1-процентную вероятность слишком большого значения, то можно использовать эту структуру данных для симуляции считывания показаний датчика генерацией случайного результата и симуляцией считывания датчиком этого результата.

Полученный мной в Stack Overflow ответ впечатлил меня по двум причинам. Во-первых, в решении мне посоветовали использовать мощную технику под названием alias-метод, которая при определённых разумных предположениях о модели машины способна после простого этапа предварительной подготовки симулировать броски кости за время $O(1)$. Во-вторых, меня ещё больше удивило то, что этот алгоритм известен в течение десятков лет, но мне он ни разу не встречался! Учитывая то, сколько вычислительного времени тратится на симуляцию, можно было бы ожидать, что эта техника известна гораздо шире. Несколько запросов в Google дали мне множество информации об этой технике, но я не смог найти ни единого сайта, где бы соединились вместе интуитивное понимание и объяснение этой техники.

Эта статья является моей попыткой сделать краткий обзор различных подходов к симуляции шулерской кости, от простых и очень непрактичных техник, до очень оптимизированного и эффективного alias-метода. Я надеюсь, что мне удастся передать различные способы интуитивного понимания задачи и то, насколько каждый из них подчёркивает какой-то новый аспект симуляции шулерской кости. Моя цель для каждого подхода заключается в исследовании мотивирующей идеи, базового алгоритма, доказательства верности и анализа времени выполнения (с точки зрения требуемых времени, памяти и случайности).

Вступление


Прежде чем переходить к конкретным подробностям различных техник, давайте сначала стандартизируем терминологию и систему обозначений.

Во введении к статье я использовал термин «шулерская кость» для описания обобщённого сценария, в котором существует конечное множество результатов, с каждым из которых связана вероятность, Формально это называется дискретным распределением вероятностей, а задача симуляции шулерской кости называется выборкой из дискретного распределения.

Для описания нашего дискретного распределения вероятностей (шулерской кости) мы будем считать, что у нас есть множество из n вероятностей $p_0, p_1, ..., p_{n - 1}$, связанных с результатами $0, 1, ..., n - 1$. Хотя результаты могут быть любыми (орёл/решка, числа на костях, цвета и т.д.), для простоты я буду считать результат каким-то положительным вещественным числом, соответствующим заданному индексу.

Работа с вещественными числами на компьютере — это «серая область» вычислений. Существует множество быстрых алгоритмов, скорость которых обеспечивается исключительно способностью за постоянное время вычислять функцию floor произвольного вещественного числа, и численные неточности в представлении чисел с плавающей запятой могут полностью разрушить некоторые алгоритмы. Следовательно, прежде чем приступать к каким-либо обсуждениям алгоритмов, работающих с вероятностями, то есть вступать в тёмный мир вещественных чисел, я должен уточнить, что может и чего не может компьютер.

Здесь и далее я буду предполагать, что все указанные ниже операции могут выполняться за постоянное время:

  • Сложение. вычитание, умножение, деление и сравнение произвольных вещественных чисел. Нам необходимо будет это делать для манипуляций с вероятностями. Может показаться, что это слишком смелое предположение, но если считать, что точность любого вещественного числа ограничена неким многчленом размера слова машины (например, 64-битное double на 32-битной машине), но я не думаю, что это слишком неразумно.
  • Генерирование равномерного вещественного числа в интервале [0, 1). Для симуляции случайности нам нужен некий источник случайных значений. Я предполагаю, что мы можем за постоянное время генерировать вещественное число произвольной точности. Это намного превышает возможности реального компьютера, но мне кажется, что в целях этого обсуждения такое допустимо. Если мы согласимся пожертвовать долей точности, сказав, что произвольное IEEE-754 double находится в интервале [0, 1], то мы и в самом деле потеряем точность, но результат, вероятно, будет достаточно точным для большинства применений.
  • Вычисление целочисленного floor (округления в меньшую сторону) вещественного числа. Это допустимо, если мы предположим, что работаем с IEEE-754 double, но в общем случае такое требование к компьютеру невыполнимо.

Стоит задаться вопросом — разумно ли считать, что мы можем выполнять все эти операции эффективно. На практике мы редко используем вероятности, указываемые до такого уровня точности, при котором свойственная IEEE-754 double ошибка округления может вызвать серьёзные проблемы, поэтому выполнить все представленные выше требования мы можем, просто работая исключительно с IEEE double. Однако если мы находимся в среде, где вероятности указываются точно как рациональные числа высокой точности, то подобные ограничения могут оказаться неразумными.

Симуляция честной кости


Прежде чем мы перейдём к более общему случаю бросания произвольной шулерской кости, давайте начнём с более простого алгоритма, который послужит строительным блоком для последующих алгоритмов: с симуляции честной n-гранной кости. Например, нам могут пригодиться броски честной 6-гранной кости при игре в Monopoly или Risk, или бросание честной монетки (двусторонней кости) и т.д.

Для этого конкретного случая есть простой, элегантный и эффективный алгоритм симуляции результата. В основе алгоритма лежит следующая идея: предположим, что мы можем генерировать действительно случайные, равномерно распределённые вещественные числа в интервале $[0, 1)$. Проиллюстрировать этот интервал можно следующим образом:


Теперь если мы хотим бросить $n$-гранную кость, то один из способов заключается в разделении интервала $[0, 1)$ на $n$ областей равного размера, каждая из которых имеет длину $\frac{1}{n}$. Это выглядит следующим образом:


Далее мы генерируем случайно выбираемое вещественное число в интервале $[0, 1)$, которое точно попадает в одну из этих маленьких областей. Из этого мы можем считать результат броска кости, посмотрев на область, в которую попало число. Например, если наше случайно выбранное значение попало в это место:


то мы можем сказать, что на кости выпало 2 (если считать, что грани кости проиндексованы с нуля).

Графически легко увидеть, в какую из областей попало случайное значение, но как нам закодировать это в алгоритме? И здесь мы воспользуемся тем фактом, что это честная кость. Поскольку все интервалы имеют равный размер, а именно $\frac{1}{n}$, то мы можем увидеть, какое наибольшее значение $i$ является таким, что $\frac{i}{n}$ не больше случайно сгенерированного значения (назовём это значение x). Можно заметить, что если мы хотим найти максимальное значение, такое, что $\frac{i}{n} \le x$, то это аналогично нахождению максимального значения $n$, такого, что $i \le xn$. Но это по определению означает, что $i = \lfloor xn \rfloor$, наибольшее натуральное число не больше xn. Следовательно, это приводит нас к такому (очень простому) алгоритму симуляции честной n-гранной кости:

Алгоритм: симуляция честной кости


  1. Генерируем равномерно распределённое случайное значение $x$ в интервале $[0, 1)$.
  2. Возвращаем $\lfloor xn \rfloor$.

Учитывая наши сделанные выше допущения о вычислениях, этот алгоритм выполняется за время $O(1)$.

Из этого раздела можно сделать два вывода. Во-первых, мы можем разделить интервал $[0, 1)$ на части так, что равномерно распределённое случайное вещественное число в этом интервале естественным образом сводится к одному из множества доступных нам дискретных вариантов. В оставшейся части статьи мы активно будем эксплуатировать эту технику. Во-вторых, может быть сложно определить, к какому конкретно интервалу относится случайное значение, но если мы знаем что-то о частях (в этом случае — что они все одинакового размера), то можно математически просто определить, к какой именно части относится конкретная точка.

Симуляция шулерской кости при помощи честной кости


Имея алгоритм симуляции честной кости, можем ли мы адаптировать его для симуляции шулерской кости? Интересно, что ответ положительный, но решение потребует больше пространства.

Из предыдущего раздела интуитивно понятно, что для симуляции броска шулерской кости нам достаточно разделить интервал $[0, 1)$ на части, а затем определить, в какую часть мы попали. Однако в общем случае это может оказаться гораздо сложнее, чем кажется. Допустим, у нас есть четырёхгранная кость с вероятностями граней $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{12}$ и $\frac{1}{12}$ (мы можем убедиться, что это правильное распределение вероятностей, ведь $\frac{1}{2} + \frac{1}{3} + \frac{1}{12} + \frac{1}{12} = \frac{6}{12} + \frac{4}{12} + \frac{1}{12} + \frac{1}{12} = \frac{12}{12}$). Если мы разделим интервал $[0, 1)$ на четыре части этих размеров, то получим следующее:


К сожалению, на этом шаге мы застрянем. Даже если бы мы знали случайное число в интервале $[0, 1)$, то не существует простых математических трюков, позволяющих автоматически определить, в какую часть попало это число. Я не хочу сказать, что это невозможно — как вы увидите, мы можем использовать множество отличных трюков — но ни один из них не имеет математической простоты алгоритма броска честной кости.

Однако мы можем адаптировать технику, используемую для честной кости, чтобы она работала и в этом случае. Давайте возьмём для примера рассмотренную выше кость. Вероятность выпадения граней равна $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{12}$ и $\frac{1}{12}$. Если мы перепишем это так, чтобы у всех членов был общий делитель, то получим значения $\frac{6}{12}$, $\frac{4}{12}$, $\frac{1}{12}$ и $\frac{1}{12}$. Поэтому мы можем воспринимать эту задачу следующим образом: вместо бросков четырёхгранной кости с взвешенными вероятностями почему бы нам не бросать 12-гранную честную кость, на гранях которой есть повторяющиеся значения? Поскольку мы знаем, как симулировать честную кость, это будет аналогом разделения интервала $[0, 1)$ на части таким образом:


Тогда мы назначим их различным результатам следующим образом:


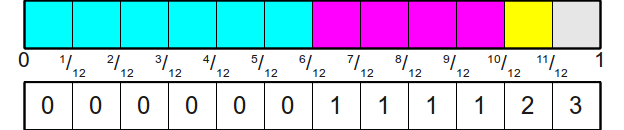
Теперь симулировать бросок кости будет очень просто — мы просто бросаем эту новую честную кость, а затем смотрим, какая грань выпала и считываем её значение. Этот первый шаг можно выполнить представленным выше алгоритмом, что даст нам целое числов в интервале $0, 1, ..., 11$. Чтобы привязать это целое число к одной из граней исходной шулерской кости, мы будем хранить вспомогательный массив из двенадцати элементов, связывающих каждое из этих чисел с исходным результатом. Графически это можно изобразить так:


Чтобы формализировать это в виде алгоритма, мы опишем и этап инициализации (получение таблицы), и этап генерации (симуляцию броска случайной кости). Оба эти этапа важно учитывать в этом и последующих алгоритмах, потому что время подготовки должно быть отличным.

На этапе инициализации мы начинаем с поиска наименьшего общего кратного всех вероятностей, заданных для граней кости (в нашем примере НОК равно 12). НОК полезно здесь, потому что оно соответствует наименьшему общему делителю, который мы можем использовать для всех дробей, а значит, и количеству граней новой честной кости, которую мы будем бросать. Получив это НОК (обозначим его L), мы должны определить, сколько граней новой кости будет распределено на каждую из граней исходной шулерской кости. В нашем примере грань с вероятностью $\frac{1}{2}$ получает шесть сторон новой кости, поскольку $\frac{1}{2} \times 12 = 6$. Аналогичным образом, сторона с вероятностью $\frac{1}{3}$ получает 4 грани, поскольку $\frac{1}{3} \times 12 = 4$. В более обобщённом виде, если L является НОК вероятностей, а $p_i$ является вероятностью выпадения грани $i$ кости, то мы выделим грани $i$ исходной шулерской кости $L \cdot p_i$ граней честной кости.

Вот псевдокод представленного выше алгоритма:

Алгоритм: симуляция шулерской кости при помощи честной кости


  • Инициализация:
    1. Находим НОК знаменателей вероятностей $p_0, p_1, ..., p_{n-1}$; обозначаем его $L$
    2. Выделяем массив $A$ размера $L$ для сопоставления результатов бросков честной кости с бросками исходной кости.
    3. Для каждой грани $i$ исходной кости выполняем в любом порядке следующее:
      1. Присваиваем следующим $L \cdot p_i$ элементам $A$ значение $i$.
  • Генерирование:
    1. Генерируем бросок честной кости для $L$-гранной кости; называем грань $S$.
    2. Возвращаем $A[S]$.

Возможно, этот алгоритм и прост, но насколько он эффективен? Само генерирование бросков кости достаточно быстрое — каждый бросок кости требует $O(1)$ времени работы для генерирования случайного броска кости с помощью предыдущего алгоритма, плюс ещё $O(1)$ времени работы на поиск по таблице. Это даёт нам общее время работы $O(1)$.

Однако этап инициализации может быть чрезвычайно затратным. Чтобы этот алгоритм заработал, нам нужно выделить пространство под массив размером с НОК знаменателей всех входных дробей. В нашем примере ($\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{12}$, $\frac{1}{12}$), он равен 12, для при других входных значениях значения могут быть патологически плохими. Например, давайте рассмотрим дроби $\frac{999999}{1000000}$ и $\frac{1}{1000000}$. НОК знаменателей равен миллиону, поэтому в нашей таблице должен быть один миллион элементов!

К сожалению, всё может быть ещё хуже. В предыдущем примере мы по крайней мере можем «ожидать», чтоб алгоритм займёт много памяти, поскольку оба знаменателя дробей равны одному миллиону. Однако у нас может появиться множество вероятностей, для которых НОК значительно больше, чем каждый отдельный знаменатель. Для примера давайте рассмотрим вероятности $\frac{1}{15}$, $\frac{1}{10}$, $\frac{5}{6}$. Здесь НОК знаменателей равно 30, что больше, чем любой из знаменателей. Конструкция здесь работает, потому что $15 = 3 \times 5$, $10 = 2 \times 5$, а $6 = 2 \times 3$; другими словами, каждый знаменатель является произведением двух простых чисел, выбранного из пула трёх значений. Поэтому их НОК является произведением всех этих простых чисел, поскольку каждый знаменатель должен являться делителем НОК. Если мы обобщим эту конструкцию и рассмотрим любое множество из $k$ простых чисел и возьмём одну дробь для каждого из попарных произведений этих простых чисел, то НОК будет гораздо больше, чем каждый отдельный знаменатель. На самом деле, одним из наилучших верхних границ, которые мы можем получить для НОК, будет $O(\prod_{i = 0}^n{d_i})$, где $d_i$ — это знаменатель $i$-той вероятности. Это не позволяет использовать такой алгоритм в реальных условиях, когда вероятности неизвестны заранее, поскольку память, необходимая для хранения таблицы размера $O(\prod_{i = 0}^n{d_i})$, может запросто оказаться больше объёма, способного поместиться в ОЗУ.

Иными словами, во многих случаях этот алгоритм ведёт себя хорошо. Если все вероятности одинаковы, то все получаемые на входе вероятности равны $\frac{1}{n}$ для какого-то $n$. Тогда НОК знаменателей равно $n$, то есть в результате бросаемая честная кость будет иметь $n$ граней, и каждая грань исходной кости будет соответствовать одной грани честной кости. Следовательно, время инициализации равно $O(n)$. Графически это можно изобразить так:


Это даёт нам следующую информацию об алгоритме:

Алгоритм Время инициализации Время генерации Занимаемая память
Наилучшее Наихудшее Наилучшее Наихудшее Наилучшая Наихудшая
Шулерская кость из честной кости $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$ $\Theta(1)$ $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$

Ещё одна важная подробность об этом алгоритме: он предполагает, что мы будем получать удобные вероятности в виде дробей с хорошими знаменателями. Если вероятности задаются как IEEE-754 double, то такой подход скорее всего ждёт катастрофа из-а небольших ошибок округления; представьте, что у нас есть вероятности 0,25 и 0,250000000001! Поэтому такой подход, вероятно, лучше не использовать, за исключением особых случаев, когда вероятности ведут себя хорошо и указаны в формате, соответствующем операциям с рациональными числами.

Симуляция несимметричной монеты


Наше объяснение простого случайного примитива (честной кости) привело к простому, но потенциально ужасно неэффективному алгоритму симуляции шулерской кости. Возможно, изучение других простых случайных примитивов прольёт немного света на другие подходы к решению этой задачи.

Простая, но на удивление полезная задача заключается в симуляции с помощью генератора случайных чисел несимметричной монеты. Если у нас есть монета с вероятностью выпадения орла $p_{heads}$, то как мы можем симулировать бросок такой несимметричной монеты?

Ранее мы выработали один интуитивно понятный подход: разбиение интервала $[0, 1)$ на последовательность таких областей, что при выборе случайного значения в интервале оно оказывается в какой-то области с вероятностью, равной размеру области. Для симуляции несимметричной монеты с помощью равномерно распределённого случайного значения в интервале $[0, 1)$ мы должны разбить интервал $[0, 1)$ следующим образом:


А потом сгенерировать равномерно распределённое случайное значение в интервале $[0, 1)$, чтобы посмотреть, в какой области оно содержится. К счастью, точка разбиения у нас только одна, поэтому очень легко определить, в какой области находится точка; если значение меньше $p_{heads}$, то на монете выпал орёл, в противном случае — решка. Псевдокод:

Алгоритм: симуляция несимметричной монеты


  1. Генерируем равномерно распределённое случайное значение в интервале $[0, 1)$.
  2. Если $x < p_{heads}$, возвращаем «орёл».
  3. Если $x \ge p_{heads}$, возвращаем «решка».

Поскольку мы можем сгенерировать равномерно распределённое случайное значение в интервале $[0, 1)$ за время $O(1)$, а также можем выполнить сравнение вещественных чисел тоже за $O(1)$, то этот алгоритм выполняется за время $O(1)$.

Симуляция честной кости с помощью несимметричных монет


Из предыдущего обсуждения мы знаем, что можно симулировать шулерскую кость с помощью честной кости, если предположить, что мы готовы потратить лишнее место в памяти. Поскольку мы можем воспринимать несимметричную монету как шулерскую двустороннюю кость, то это значит, что мы можем симулировать несимметричную монету с помощью честной кости. Интересно, что можно сделать и обратное — симулировать честную кость с помощью несимметричной монеты. Конструкция получается простой, элегантной и её можно легко обобщить для симуляции шулерской кости с помощью множества несимметричных монет.

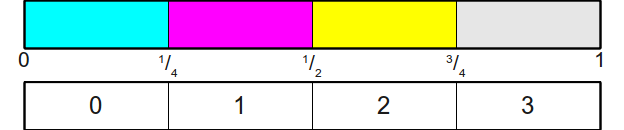
Конструкция для симуляции несимметричной монеты разбивает интервал $[0, 1)$ на две области — область «орлов» и область «решек» на основании вероятности выпадения на кости орлов. Мы уже видели подобный трюк, использованный для симуляции честной $n$-гранной кости: интервал $[0, 1)$ делился на $n$ равных областей. Например, при броске четырёхгранной кости у нас получалось следующее разделение:


Теперь предположим, что нас интересует симуляция броска этой честной кости с помощью набора несимметричных монет. Один из способов решения заключается в следующем: представьте, что мы обходим эти области слева направо, каждый раз спрашивая, хотим ли мы останавливаться в текущей области, или будем двигаться дальше. Например, давайте предположим, что мы хотим выбрать случайным образом одну из этих областей. Начиная с самой левой области, мы будем подбрасывать несимметричную монету, которая сообщает нам, должны ли мы остановиться в этой области, или продолжить движение дальше. Поскольку нам нужно выбирать из всех этих областей равномерно с вероятностью $\frac{1}{4}$, то мы можем сделать это, подбрасывая несимметричную монету, орлы на которой выпадают с вероятностью $\frac{1}{4}$. Если выпадает орёл, то мы останавливаемся в текущей области. В противном случае мы двигаемся в следующую область.

Если монеты падают решкой вверх, то мы оказывается во второй области и снова спрашиваем, должны ли мы снова выбрать эту область или продолжать движение. Вы можете подумать, что для этого мы должны бросить ещё одну монету с вероятностью выпадения орла $\frac{1}{4}$, но на самом деле это неверно! Чтобы увидеть недостаток в этом рассуждении, мы должны дойти до крайней ситуации — если в каждой области мы бросаем монету, на которой выпадает орёл с вероятностью $\frac{1}{4}$, то есть небольшая вероятность, что в каждой области монета выпадет решкой, то есть нам придётся отказаться от всех областей. При движении по областям нам каким-то образом нужно продолжать увеличивать вероятность выпадения на монете орла. В крайней ситуации, если мы окажемся в последней области, то на монете должен быть орёл с вероятностью $1$, поскольку если мы отклонили все предыдущие области, то правильным решением будет остановиться в последней области.

Чтобы определить вероятность, с которой наша несимметричная монета должна выбрасывать орла после пропуска первой области, нам нужно заметить, что после пропуска первой области их осталось всего три. Поскольку мы бросаем честную кость, нам нужно, чтобы каждая из этих трёх областей была выбрана с вероятностью $\frac{1}{3}$. Следовательно, интуитивно кажется, что у нас должна быть вторая кость, на которой выпадает орёл с вероятностью $\frac{1}{3}$. Используя аналогичные рассуждения, можно понять, что при выпадании во второй области решки в третьей области монета должна выпадать орлом с вероятностью $\frac{1}{2}$, а в последней области — с вероятностью $1$.

Такое интуитивное понимание приводит нас к следующему алгоритму. Заметьте, что мы не обсуждали правильность или ошибочность этого алгоритма; вскоре мы этим займёмся.

Алгоритм: симуляция честной кости с помощью несимметричных монет


  1. For $i = 0$ to $n - 1$:
    1. Бросаем несимметричную монету с вероятностью выбрасывания орла $\frac{1}{n - i}$.
    2. Если выпадает орёл, то возвращаем $i$.

Этот алгоритм прост и в наихудшем случае выполняется за время $O(n)$. Но как нам проверить, правилен ли он? Чтобы узнать это, нам потребуется следующая теорема:

Теорема: приведённый выше алгоритм возвращает сторону $i$ с вероятностью $\frac{1}{n}$ для любого выбранного $i$.

Доказательство: рассмотрим любое постоянное $n \ge 0$. Мы доказываем с помощью сильной индукции, что каждая из $n$ граней имеет вероятность выбора $\frac{1}{n}$.

Для нашего примера мы показываем, что грань $0$ кости имеет вероятность выбора $\frac{1}{n}$. Но это непосредственно следует из самого алгоритма — мы выбираем грань 0, если на несимметричной монете с вероятностью выпадения орла $\frac{1}{n}$ выпадает орёл, то есть мы выбрали её с вероятностью $\frac{1}{n}$.

Для этапа индукции предположим для граней $0, 1, 2, ..., k - 1$, что эти грани выбираются с вероятностью $\frac{1}{n}$ и рассмотрим вероятность выбора грани $k$. Грань $k$ будет выбрана тогда и только тогда, когда не выбраны первые $k$ граней, а на монете с вероятностью выпадения орла $\frac{1}{n - k}$ выпал орёл. Поскольку каждая из первых $k$ граней имеет вероятность выбора $\frac{1}{n}$, и поскольку выбирается только одна грань, то вероятность выбора одной из первых граней $k$ задаётся как $\frac{k}{n}$. Это значит, что вероятность того, что алгоритм не выберет одну из первых $k$ граней равен $1 - \frac{k}{n} = \frac{n}{n} - \frac{k}{n} = \frac{n - k}{n}$. То есть вероятность выбора грани $k$ задаётся как $\frac{n - k}{n} \frac{1}{n - k} = \frac{1}{n}$, что и требуется показать. Таким образом, каждая грань кости выбирается равномерно и случайно.

Разумеется, алгоритм довольно неэффективен — с помощью первой техники мы можем симулировать бросок честной кости за время $O(1)$! Но этот алгоритм можно использовать как ступеньку к достаточно эффективному алгоритму симуляции шулерской кости с помощью несимметричных монет.

Симуляция шулерской кости с помощью несимметричных монет


Представленный выше алгоритм интересен тем, что даёт нам простой каркас для симуляции кости с помощью набора монет. Мы начинаем с броска монеты для определения того, нужно ли выбрать первую грань кости или двигаться к оставшимся. При этом процессе нам нужно внимательно обращаться с изменением масштаба оставшихся вероятностей.

Давайте посмотрим, как можно использовать эту технику для симуляции броска шулерской кости. Воспользуемся нашим примером с вероятностями $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{12}$, $\frac{1}{12}$. Он, если вы не помните, делит интервал $[0, 1)$ следующим образом:


Теперь давайте подумаем о том, как можно симулировать такую шулерскую кость с помощью несимметричных монет. Мы можем начать с броска монеты с вероятностью выпадения орла $\frac{1}{2}$ для определения того, должны ли мы возвращать грань 0. Если на этой монете выпадает орёл, то отлично! Мы закончили. В противном случае нам нужно бросить ещё одну монету, чтобы решить, нужно ли выбирать следующую грань. Как и ранее, несмотря на то, что следующая грань имеет вероятность выбора $\frac{1}{3}$, мы не хотим бросать монету, на которой орёл выпадает с вероятностью $\frac{1}{3}$, потому что половина «массы» вероятностей была отброшена, когда мы не выбрали грань с $\frac{1}{2}$. На самом деле, поскольку половина массы вероятностей исчезла, то если мы заново нормализуем оставшиеся вероятности, то получим обновлённые вероятности: $\frac{2}{3}$, $\frac{1}{6}$, $\frac{1}{6}$. Следовательно, вторую монету надо кидать с вероятностью $\frac{2}{3}$. Если эта монета тоже выпадет решкой, то нам придётся выбирать между двумя сторонами $\frac{1}{12}$. Поскольку на этом этапе мы избавимся от $\frac{5}{6}$ массы вероятностей, то можем заново нормализировать вероятности сторон $\frac{1}{12}$ так, чтобы каждая имела вероятность $\frac{1}{2}$ выпадения орла, то есть у третьей монеты будет вероятность $\frac{1}{2}$. Последняя монета, если до неё когда-нибудь дойдёт дело, должна выбрасывать орла с вероятностью $1$, поскольку это самая последняя область.

Подведём итог — вероятности монет будут следующими:

  1. Первый бросок: $\frac{1}{2}$
  2. Второй бросок: $\frac{2}{3}$
  3. Третий бросок: $\frac{1}{2}$
  4. Четвёртый бросок: $1$

Может быть интуитивно понятно, откуда берутся эти числа, но чтобы превратить подбор в алгоритм, нам придётся создать формальную конструкцию выбора вероятностей. Идея будет следующей — на каждом этапе мы запоминаем оставшуюся часть массы вероятностей. В начале, до броска первой монеты, она равна $1$. После броска первой монеты $1 - p_0$. После броска второй монеты $1 - p_0 - p_1$. В более общем виде после броска $k$ остаток массы вероятности равен $1 - \sum_{i = 0}^{k - 1}{p_i}$. Каждый раз, когда мы бросаем монету, чтобы определить, выбирать или нет область $k$, мы в результате бросаем монету, вероятность выпадения орла на которой равна доле оставшейся вероятности, занятой вероятностью $p_k$, что задаётся как $\frac{p_k}{1 - \sum_{i = 0}^{k - 1}{p_i}}$. Это даёт нам следующий алгоритм симуляции шулерской кости набором несимметричных монет (мы докажем его правильность и время выполнения чуть ниже):

Алгоритм: шулерская кость из несимметричных монет


  • Инициализация:
    1. Сохраняем вероятности $p_i$ для дальнейшего использования.
  • Генерирование:
    Задаём $mass = 1$
    For $i = 0$ to $n - 1$:
    1. Бросаем несимметричную монету с вероятностью выпадения орла $\frac{p_i}{mass}$.
    2. Если выпал орёл, то возвращаем $i$.
    3. В противном случае задаём $mass = mass - p_i$

С интуитивной точки зрения это логично, но верно ли это математически? К счастью, ответ положительный благодаря обобщению вышеприведённого доказательства:

Теорема: показанный выше алгоритм возвращает грань $i$ с вероятностью $p_i$ при любом выбранном $i$.

Доказательство: рассмотрим любое постоянное $n \ge 0$. С помощью сильной индукции мы доказываем, что каждая из $n$ граней имеет вероятность выбора $p_i$.

В качестве базового случая докажем, что грань $0$ кости имеет вероятность выбора $p_0$. Мы выбираем грань $0$, если при броске самой первой монеты получаем орла, что происходит с вероятностью $\frac{p_0}{mass}$. Поскольку $mass$ изначально равна $1$, то эта вероятность равна $\frac{p_0}{1} = p_0$, то есть грань 0 выбирается с вероятностью $p_0$, как и требуется.

Для этапа индукции предположим, чтоб грани $0, 1, ..., k - 1$ выбираются с вероятностью $p_0, p_1, ..., p_{k-1}$ и рассмотрим вероятность выбора ребра $k$. Грань $k$ будет выбрана тогда и только тогда, когда не выбраны первые $k$ граней, после чего на монете с вероятностью выпадения орла $\frac{p_k}{mass}$ выпадает орёл. Поскольку каждая из первых $k$ граней была выбрана с правильной вероятностью, а выбирается всегда только одна грань, то вероятность выбора одной из первых $k$ задаётся как $\sum_{i = 0}^{k - 1}{p_i}$. Это означает, что вероятность не выбора алгоритмом одной из первых $k$ граней задаётся как $1 - \sum_{i = 0}^{k - 1}{p_i}$. Вероятность того, что монета для грани $k$ выпадет орлом, задаётся как $\frac{p_k}{mass}$ и после $k$ итераций мы можем при помощи быстрой индукции увидеть, что $mass = 1 - \sum_{i = 0}^{k - 1}{p_i}$. Это означает, что общая вероятность выбора грани $k$ задаётся как $(1 - \sum_{i = 0}^{k - 1}{p_i})\frac{p_k}{1 - \sum_{i = 0}^{k - 1}{p_i}} = p_k$, как и требовалось.

Теперь давайте оценим временную сложность этого алгоритма. Мы знаем, что время инициализации может быть $\Theta(1)$, если мы сохраняем поверхностную копию входного массива вероятностей, но может быть и $\Theta(n)$, чтобы мы могли сохранить собственную версию массива (на случай, если вызывающая функция захочет изменить его в дальнейшем). Сама генерация результата броска кости может потребовать в худшем случае $\Theta(n)$ бросков, и всего один бросок в лучшем случае.

Однако после размышлений становится понятно, что на количество необходимых бросков монет сильно влияет входящее распределение. В самом наилучшем случае у нас будет распределение вероятностей, при котором вся масса вероятностей сосредоточена на первой грани кости, а все остальные вероятности равны нулю. В таком случае нам достаточно одного броска монеты. В самом наихудшем случае вся масса вероятностей сосредоточена в самой последней грани кости, а на всех остальных гранях равна нулю. В таком случае нам для получения результата придётся бросать $n$ монет.

Мы можем чётким и математическим образом характеризовать ожидаемое количество бросков монеты в этом алгоритме. Давайте представим случайную переменную $X$, обозначающую количество бросков монет при любом выполнении этого алгоритма для некого конкретного распределения. То есть $\mathbb{P}[X = 1]$ является вероятностью того, что для завершения алгоритму достаточно бросить одну монету, $\mathbb{P}[X = 2]$ — вероятность того, что алгоритм бросит две монеты, и т.д. В таком случае ожидаемое количество бросков монет для нашего алгоритма определяется математическим ожиданием $X$, обозначаемым как $\mathbb{E}[X]$. По определению мы получаем, что

$\mathbb{E}[X] = \sum_{i = 1}^n{i \cdot \mathbb{P}[X = i]}$


Каково же значение $\mathbb{P}[X = i]$? Алгоритм завершает работу после выбора какой-то грани кости. Если он выбирает грань $0$, то бросит одну монету. Если он выберет грань $1$, то будет бросать две монеты — одну чтобы понять, что не хочет выбирать грань $0$, другую чтобы понять, что хочет выбрать грань $1$. Если более обобщённо, то если алгоритм выбирает грань $i$, то он бросит $i + 1$ монет: $i$ монет, чтобы решить, что он не хочет выбирать предыдущие $i - 1$ граней, и одну, чтобы решить, что выбирает грань $i$. В сочетании с тем фактом, что мы знаем о выборе грани $i$ с вероятностью $p_i$, это значит, что

$\mathbb{E}[X] = \sum_{i = 1}^n{i \cdot \mathbb{P}[X = i]} = \sum_{i = 1}^n{i \cdot p_{i - 1}} = \sum_{i = 1}^n{((i - 1) p_{i - 1} + p_{i - 1})} = \sum_{i = 1}^n{((i - 1) p_{i - 1})} + \sum_{i = 1}^n{p_{i - 1}}$


Заметьте, что в последнем упрощении первый член эквивалентен $\sum_{i = 0}^{n-1}{i \cdot p_i}$, что эквивалентно $\mathbb{E}[p]$, ожидаемому результату броска кости! Более того, второй член равен $1$, поскольку это сумма всех вероятностей. Это значит, что $\mathbb{E}[X] = \mathbb{E}[p] + 1$. То есть ожидаемое количество бросков монет равно единице плюс математическое ожидание броска кости!

Алгоритм Время инициализации Время генерации Занятая память
Наилучшее Наихудшее Наилучшее Наихудшее Наилучшая Наихудшая
Шулерская кость из честной кости $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$ $\Theta(1)$ $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$
Шулерская кость из несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ $\Theta(n)$

Обобщение несимметричных монет: симуляция шулерской кости


В показанном выше примере мы смогли эффективно симулировать несимметричную монету, поскольку нам необходимо было учитывать только одну точку разбиения. Как нам эффективно обобщить эту идею до шулерской кости, в которой количество граней может быть произвольным?

Как можно заметить, несимметричная монета — это шулерская кость, только с двумя гранями. Следовательно, мы можем воспринимать несимметричную монету просто как особый случай более общей задачи, которую хотим решить. При решении задачи несимметричной монеты мы разделяем интервал $[0, 1)$ на две области — одна для орла, вторая для решки — а затем для нахождения области используем тот факт, что присутствует только одна точка разбиения. Если у нас n-гранная кость, то областей будет больше, а значит и несколько разделительных точек. Предположим, например, что у нас есть семигранная кость с вероятностями $\frac{1}{4}$, $\frac{1}{5}$, $\frac{1}{8}$, $\frac{1}{8}$, $\frac{1}{10}$, $\frac{1}{10}$, $\frac{1}{10}$. Если мы хотим разделить интервал $[0, 1)$ на семь частей, то сделаем это следующим образом:


Заметьте, где расположены эти области. Первая область начинается с $0$ и заканчивается $\frac{1}{4}$. Вторая область начинается с $\frac{1}{4}$ и заканчивается в $\frac{1}{4} + \frac{1}{5} = \frac{9}{20}$. В более общем виде, если вероятности равны $p_0, p_1, ..., p_{n - 1}$, то области будут являться интервалами $[0, p_0)$, $[p_0, p_0 + p_1)$, $[p_0 + p_1, p_0 + p_1 + p_2)$ и т.д. То есть область $i$ ограничена интервалом

$[\sum_{j = 0}^{i - 1}{p_j}, \sum_{j = 0}^{i}{p_j})$


Заметьте, что разность между этими двумя значениями равна $p_i$, то есть общая площадь области равна $p_i$, как и требуется.

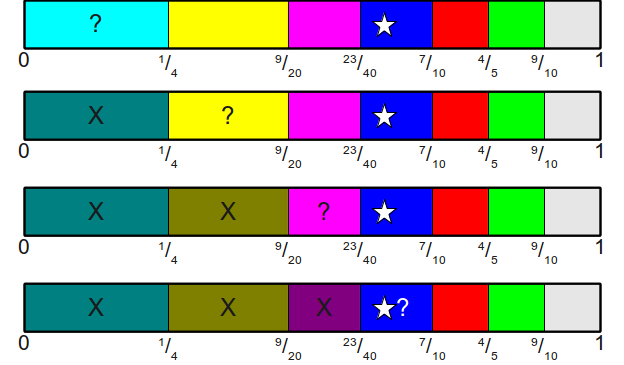
Теперь мы знаем, где находятся области. Если мы хотим выбрать равномерно распределённое случайное значение $x$ в интервале $[0, 1)$, то как нам определить, в какой интервал оно попадает? Если воспользоваться в качестве начальной точки нашим алгоритмом несимметричной монеты, то идея будет заключаться в следующем: начиная с конечной точки первой области, постоянно двигаться вверх по всем областям, пока мы не найдём конечную точку, значение которой больше значения $x$. Если мы так сделаем, то найдём первую область, содержащую точку $x$, а значит и наше значение. Например, если мы выбрали случайное значение $x = \frac{27}{40}$, то выполним следующий поиск:


Из чего мы можем заключить, что на кости с индексацией с нуля выпала грань 3.

Такой алгоритм линейного сканирования даст нам алгоритм времени $O(n)$ для нахождения выброшенной грани кости. Однако мы можем значительно улучшить время его выполнения, воспользовавшись следующим наблюдением: ряд конечных точек областей образует возрастающую последовательность (поскольку мы всегда прибавляем всё больше и больше вероятностей, ни одна из которых не может быть меньше нуля). Следовательно, мы хотим ответить на следующий вопрос: имея возрастающую последовательность значений и некую проверочную точку, нужно найти первое значение в интервале, строго большее проверочной точки. Это идеальный момент для использования двоичного поиска! Например, вот выполнение двоичного поиска по приведённому выше массиву для нахождения области, к которой принадлежит $x = \frac{39}{40}$:


Это даёт нам алгоритм со временем $\Theta(\log n)$ для привязки равномерно распределённого случайного значения в интервале $[0, 1)$ к грани брошенной кости. Более того, для построения таблицы конечных точек достаточно времени предварительной обработки $\Theta(n)$; мы просто вычисляем частичные суммы вероятностей при движении вверх.

Этот алгоритм иногда называют алгоритмом выбора колесом рулетки, потому что он выбирает случайную область с помощью техники, похожей на колесо рулетки — броском шарика в интервал и наблюдением за тем, где он остановится. В псевдокоде алгоритм выглядит так:

Алгоритм: выбор колесом рулетки


  • Инициализация:
    1. Выделяем массив $A$ размера $n$
    2. Задаём $A[0] = p_0$.
    3. Для каждой вероятности $i$ от $1$ до $n - 1$:
      1. Задаём $A[i] = A[i - 1] + p_i$

  • Генерация:
    1. Генерируем равномерно распределённое случайное значение $x$ в интервале $[0, 1)$
    2. С помощью двоичного поиска находим индекс $i$ наименьшего элемента $A$, который меньше $x$.
    3. Возвращаем $i$.

Сравнение между этим алгоритмом и приведённым ранее выглядит довольно впечатляюще:

Алгоритм Время инициализации Время генерации Занятая память
Наилучшее Наихудшее Наилучшее Наихудшее Наилучшая Наихудшая
Шулерская кость из честной кости $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$ $\Theta(1)$ $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$
Шулерская кость из несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ $\Theta(n)$
Выбор колесом рулетки $\Theta(n)$ $\Theta(\log n)$ $\Theta(n)$

Очевидно, что теперь у нас есть гораздо лучший алгоритм, чем изначальный. Дискретизация вероятностей только поначалу казалась многообещающей, но этот новый подход, основанный на непрерывном значении и двоичном поиске, выглядит гораздо лучше. Однако всё ещё возможно улучшить эти показатели с помощью умного использования набора гибридных техник, которые мы рассмотрим чуть ниже.

Интересная деталь этого алгоритма заключается в том, что хотя использование двоичного поиска гарантирует время наихудшего времени генерации случайных чисел $O(\log n)$, он также не позволяет осуществлять более быстрый поиск; то есть время генерации тоже будет равно $\Omega(\log n)$. Можно ли его улучшить? Оказывается, что можно.

Допустим мы перейдём от двоичного поиска по списку накапливаемых вероятностей к использованию двоичного дерева поиска. Например, имея приведённое выше множество вероятностей, мы можем построить для их накапливаемого распределения следующее двоичное дерево поиска:


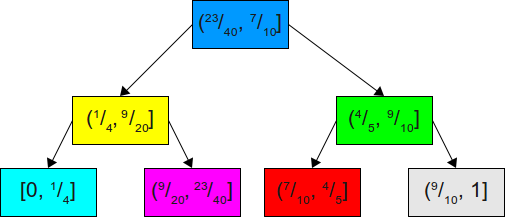
Теперь, если мы захотим симулировать бросок кости, то сможем сгенерировать равномерно распределённое число в интервале $[0, 1)$, а затем посмотреть, в каком интервале оно лежит в этом двоичном дереве поиска (BST). Поскольку это сбалансированное двоичное дерево поиска, наилучшее время поиска равно $O(1)$, а наихудшее — $O(\log n)$.

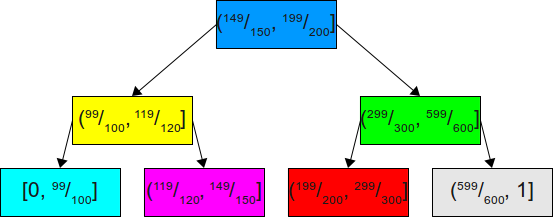
Однако если предположить, что мы знаем больше о распределении вероятностей, то можно сделать гораздо лучше. Например, предположим, что наши вероятности равны $\frac{99}{100}$, $\frac{1}{600}$, $\frac{1}{600}$, $\frac{1}{600}$, $\frac{1}{600}$, $\frac{1}{600}$, $\frac{1}{600}$. То есть распределение вероятностей чрезвычайно перекошено, а почти вся масса вероятностей сконцентрирована на одной грани. Мы можем построить для этих вероятностей сбалансированное BST:


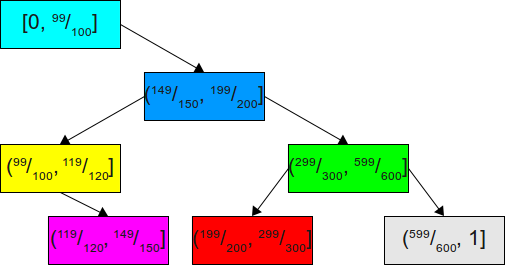
Хотя это двоичное дерево поиска идеально сбалансировано, для наших задач оно не очень подходит. Поскольку мы знаем, что в 99 из 100 случаев случайное значение будет находиться в интервале $[0, \frac{99}{100})$, то нет никакого смысла хранить узел для этого интервала там, где он расположен сейчас. На самом деле это будет означать, что почти всё время мы будем выполнять два ненужных сравнения с синей и жёлтой областью. Поскольку с очень высокой вероятностью нам первым стоит проверять самый большой интервал, то логично будет разбалансировать дерево так, чтобы сделать средний случай значительно лучше за счёт оставшихся. Это показано здесь:


Теперь мы скорее всего будем завершать поиск, сразу же найдя нужную область после первой попытки. В очень маловероятном случае, когда нужная область находится в оставшихся $(\frac{99}{100}, 1]$ мы спокойно спустимся до конца дерева, которое на самом деле хорошо сбалансировано.

В обобщённом виде мы хотим решить следующую задачу:

При заданном множестве вероятностей найти двоичное дерево поиска этих вероятностей, минимизирующее ожидаемое время поиска.

К счастью, эта задача очень хорошо изучена и называется задачей оптимального двоичного дерева поиска. Существует множество алгоритмов для решения этой задачи; известно, что точное решение можно найти за время $O(n^2)$ с помощью динамического программирования, и что существуют хорошие алгоритмы линейного времени, способные находить приблизительные решения. Кроме того, для получения постоянного множителя оптимального решения можно использовать структуру данных splay tree (расширяющееся дерево) (самобалансирующееся двоичное дерево поиска).

Интересно что наилучший случай поведения таких оптимизированных двоичных деревьев поиска возникает, когда распределения вероятностей чрезвычайно перекошены, поскольку мы просто можем переместить в корень дерева узлы, содержащие подавляющую часть массы вероятностей, а наихудший случай — это когда распределение сбалансировано, потому что тогда дерево должно быть широким и неглубоким. Это противоположно поведению предыдущего алгоритма, в котором для симуляции шулерской кости использовалась честная!

В наилучшем случае у нас есть шулерская кость, в которой всегда выпадает одна грань (то есть она имеет вероятность 1, а все остальные грани имеют вероятность 0). Это чрезвычайное преувеличение нашего предыдущего примера, но в таком случае поиск будет всегда завершаться после первой попытки. В наихудшем случае все вероятности равны, и у нас получается стандартный поиск по BST. Мы приходим к следующему:

Алгоритм Время инициализации Время генерации Занятая память
Наилучшее Наихудшее Наилучшее Наихудшее Наилучшая Наихудшая
Шулерская кость из честной кости $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$ $\Theta(1)$ $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$
Шулерская кость из несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ $\Theta(n)$
Выбор колесом рулетки $\Theta(n)$ $\Theta(\log n)$ $\Theta(n)$
Оптимальный выбор колесом рулетки $O(n^2)$ $\Theta(1)$ $O(\log n)$ $\Theta(n)$

Бросание дротиков


Пока мы рассматривали два примитива, которые помогли нам построить алгоритмы для симуляции шулерской кости: честную кость и несимметричную монету. При использовании только честной кости мы приходим к (увы, непрактичному) алгоритму симуляции шулерской кости, а начав с несимметричными монетами, смогли изобрести быстрый алгоритм симуляции шулерской кости. Можно ли скомбинировать эти два подхода, чтобы создать алгоритм на основе и честных костей, и несимметричных монет? Оказывается, что да, и на самом деле получающийся алгоритм лучше обоих этих подходов.

До этого момента мы визуализировали интервал $[0, 1)$ и вероятности граней костей как одномерный интервал. Оба эти алгоритма выбирают какую-то точку в интервале $[0, 1)$ и накладывают её на отрезок прямой, длина которого соответствует какой-то вероятности. Чем длиннее отрезки мы создаём, тем больше вероятность выбора этого отрезка. Но что, если попробовать думать не в одном, а в двух измерениях? Что, если мы будем считать вероятность $p_i$ не длиной отрезка прямой, а площадью прямоугольника?

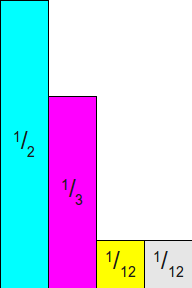
Давайте начнём с возврата к нашему предыдущему примеру с вероятностями $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{12}$, $\frac{1}{12}$. Изобразим эти вероятности в виде прямоугольников шириной $w$ (с каким-то произвольным $w > 0$) и высотой $p_i$ (таким образом, площадь прямоугольника будет равна $w \cdot p_i$):


Заметьте, что общая площадь этих прямоугольников равна $w$, поскольку площадь

$\sum_{i = 0}^{n - 1}{w p_i} = w \sum_{i = 0}^{n - 1}{p_i} = w$


Теперь предположим, что мы нарисуем вокруг этих прямоугольников ограничивающий прямоугольник, ширина которого равна $4w$ (поскольку четырёхугольников четыре), а высота равна $\frac{1}{2}$ (так как самый высокий прямоугольник имеет высоту $\frac{1}{2}$):


Мы можем представить, что этот прямоугольник разделён на пять областей — четыре области соответствуют различным вероятностям, а одной областью обозначено неиспользуемое пространство. Взяв это разбиение, мы можем подумать об алгоритме симуляции случайных бросков кости как об игре в дартс. Предположим, что мы бросаем в эту цель (идеально равномерно распределённый) дротик. Если он попадает в неиспользуемое пространство, то мы достаём дротик и бросаем его снова, повторяя процесс, пока не попадём в один из прямоугольников. Поскольку чем больше вероятность, тем больше прямоугольник, то чем больше вероятность выбрасывания грани кости, тем выше вероятность попадания в её прямоугольник. На самом деле если мы поставим условие, что уже попали в какой-то прямоугольник, то у нас получится следующее:

$\mathbb{P}[\mbox{hit rectangle for side i} | \mbox{hit some rectangle}] = \frac{\mbox{area of rectangle for i}}{\mbox{total rectangle area}} = \frac{w p_i}{w} = p_i$


Другими словами, когда мы наконец попадаем в какой-то прямоугольник своим равномерно распределённым дротиком, мы выбираем прямоугольник грани $i$ шулерской кости с вероятностью $p_i$, то есть именно с той вероятностью, которая нам нужна! То есть если мы сможем найти какой-то эффективный способ симуляции бросков случайных дротиков в этот прямоугольник, то у нас будет эффективный способ симуляции броска случайной кости.

Один из способов имитации бросков дротика в этот прямоугольник заключается в выборе двух равномерно распределённых значений в интервале $[0, 1)$, масштабировании их под соответствующую ширину и высоту с последующей проверкой области под дротиком. Однако при этом возникает та же проблема, которая у нас была, когда мы пытались определить одномерную область, в которой находится случайное значение. Однако существует поистине прекрасная серия наблюдений, благодаря которой определение места попадания может стать простой, если не тривиальной, задачей.

Первое наблюдение: мы показали, что ширину этих прямоугольников можно выбирать произвольно, потому что все они имеют равную ширину. Высоты, разумеется, зависят от вероятностей граней костей. Однако если мы равномерно отмасштабируем все высоты на какое-то положительное вещественное число $h$, то относительные области всех прямоугольников будут такими же. На самом деле для любого положительного вещественного числа $h$ общая площадь всех прямоугольников после масштабирования их высот на $h$ вычисляется как

$\sum_{i = 0}^{n - 1}{w h p_i} = w h \sum_{i = 0}^{n - 1}{p_i} = w h$


Теперь рассмотрим вероятность выбора любого отдельного прямоугольника, ограничившись условием, что мы точно попали в какой-то прямоугольник. Используя те же расчёты, мы получаем следующее:

$\mathbb{P}[\mbox{hit rectangle for side i} | \mbox{hit some rectangle}] = \frac{\mbox{area of rectangle for i}}{\mbox{total rectangle area}} = \frac{w h p_i}{w h} = p_i$


То есть на самом деле вероятность выбора любого отдельного прямоугольника не изменяется, если мы масштабируем их линейно и равномерно.

Поскольку мы можем выбрать любой подходящий коэффициент масштабирования, то почему бы нам не отмасштабировать эти прямоугольники так, чтобы высота ограничивающего прямоугольника всегда равнялась 1? Так как высота ограничивающего прямоугольника определяется максимальным значением $p_i$ входных вероятностей, то мы можем начать с масштабирования каждого из прямоугольников на коэффициент $\frac{1}{p_{max}}$, где $p_{max}$ — это максимальная вероятность всех входных вероятностей. Благодаря этому мы получаем высоту прямоугольника 1. Аналогичным образом, поскольку мы можем выбирать для прямоугольников любую произвольную ширину, давайте возьмём ширину 1. Это значит, что при $n$ вероятностях общая ширина ограничивающего прямоугольника равна $n$, а общая высота — 1. Это показано на рисунке:


Теперь мы готовы подумать о том, как мы можем бросить случайный дротик в прямоугольник и определить, во что он попал. Самое важное заключается в том, что мы можем разбить прямоугольник так, чтобы он не состоял из нескольких более мелких прямоугольников и пустого пространства странной формы. Вместо этого область разрезается на набор из $2n$ прямоугольников, по два на каждую из $n$ входных вероятностей. Это показано здесь:


Заметьте, как образуется этот прямоугольник. Для каждой грани шулерской кости у нас есть один столбец шириной 1 и высотой 1, разделённая на два пространства — полупространство «да», соответствующее прямоугольнику этого размера, и полупространство «нет», соответствующее оставшейся части столбца.

Теперь давайте подумаем, как мы можем бросать дротик. Идеально равномерный дротик, брошенный в этот прямоугольник, будет иметь компоненты $x$ и $y$. Здесь компонент $x$, который должен находиться в интервале $[0, 1)$, соответствует тому, в какой столбец попадёт дротик. Компонент $y$, который должен находиться в интервале $[0, 1)$, соответствует тому, насколько высоко мы находимся в столбце. Выбор компонента $x$ влияет на то, какую грань шулерской кости мы рассматриваем, а выбор компонента $y$ соответствует тому, выбрали мы эту грань или нет. Но постойте — нам уже известны эти две идеи! Выбор координаты $x$, соответствующей столбцу, аналогично броску честной кости для решения о выборе столбца. Выбор координаты $y$ соответствует броску несимметричной монеты для определения того, нужно ли выбирать грань, или бросать снова! Это наблюдение так важно, что нам сделать его абсолютно понятным:

Выбор случайной точки в этом интервале аналогичен бросанию честной кости и броску несимметричной монеты.

На самом деле этот результат можно воспринимать как гораздо более мощную возможность. Для симуляции шулерской кости мы строим набор несимметричных монет, по одной для каждой грани кости, а затем бросаем честную кость для определения того, какую монету нам бросать. На основании броска кости, если на соответствующей монете выпал орёл, то мы выбираем соответствующую грань, а если выпала решка, то бросаем кость снова и повторяем процесс.

Давайте повторим эти важные моменты. Во-первых, эти прямоугольники имеют следующие размеры — для каждой грани высота прямоугольника «да» задаётся как $\frac{p_i}{p_{max}}$, а высота прямоугольника «нет» задаётся как $\frac{p_{max} - p_i}{p_{max}}$. Так мы выполняем нормализацию, чтобы общие высоты прямоугольников были равны 1. Во-вторых, каждый прямоугольник имеет ширину $1$, однако на самом деле это значение не важно. Наконец, алгоритм имеет следующий вид: пока мы не выбрали какой-то результат, бросаем честную кость для определения того, в каком столбце мы находимся (другими словами, какую несимметричную монету нам нужно бросать). Далее бросаем соответствующую монету. Если выпадает орёл, то выбираем результат, соответствующий выбранному столбцу. В противном случае повторяем этот процесс.

Алгоритм: шулерская кость из честных костей/несимметричных монет


  • Инициализация:
    1. Находим максимальное значение $p_i$; называем его $p_{max}$.
    2. Выделяем массив $Coins$ длиной $n$, соответствующий высотам прямоугольников «да» в каждой строке.
    3. Для каждой вероятности $i$ от $0$ до $n - 1$:
      1. Задаём $Coins[i] = \frac{p_i}{p_{max}}$

  • Генерация:
    1. Пока не найдено значение:
      1. Бросаем честную n-гранную кость и получаем индекс $i$ в интервале $[0, n)$.
      2. Бросаем несимметричную монету, на которой выпадает орёл с вероятностью $Coins[i]$.
      3. Если на монете выпадает орёл, то возвращаем $i$.

Давайте проанализируем сложность этого алгоритма. На этапе инициализации поиск максимальной вероятности занимает время $O(n)$, а затем ещё нужно дополнительное время $O(n)$ на выделение и заполнение массива $Coins$, то есть общее время инициализации равно $O(n)$. На этапе генерации в наилучшем случае мы выбросим орла на самой первой монете, закончив за $O(1)$. Но сколько итераций требуется для ожидания? Чтобы найти это значение, давайте вычислим вероятность того, что мы выберем какую-то грань после первой итерации. Поскольку у монет вероятность выбрасывания орла неодинакова, то это будет зависеть от выбранной монеты. К счастью, поскольку мы выбираем каждую монету с равной вероятностью (а именно $\frac{1}{n}$), вычисления становятся намного проще. Более того, поскольку в результате мы бросаем только одну монету, то события выбора каждой монеты и выбрасывания орла исключают друг друга, то есть общая вероятность того, что какая-то монета будет выбрана, брошена и даст нам орла вычисляется как сумма вероятностей выбора каждой отдельной монеты и выбрасывания орла на каждой этой монете. Поскольку мы знаем, что вероятность выбора грани $i$ задаётся как $\frac{p_i}{p_{max}}$, то общая вероятность выбора какой-то стороны задаётся как

$\sum_{i = 0}^{n - 1}{(\frac{1}{n} \frac{p_i}{p_{max}})} = \frac{1}{n}\sum_{i = 0}^{n - 1}{\frac{p_i}{p_{max}}} = \frac{1}{n \cdot p_{max}}\sum_{i = 0}^{n - 1}{p_i} = \frac{1}{n \cdot p_{max}}$


Если это вероятность выбора какой-то монеты в любой одной итерации, то ожидаемое количество итераций, которое может произойти, задаётся величиной, обратной этой дроби, то есть $n \cdot p_{max}$. Но что же это значит? Она очень сильно зависит от выбора $p_{max}$. В одном предельном случае $p_{max}$ может быть равна $1$ (то есть кость всегда выпадает одной гранью). В этом случае ожидаемое количество итераций равно $n$, то есть для получения ожидаемого мы должны бросить честную кость $n$ раз. Это логично, потому что единственный способ выбора грани заключается в том, что мы берём несимметричную монету для одной грани, которая всегда падает орлом вверх, поскольку у каждой другой стороны монета никогда не выпадает орлом. С другой стороны, в противоположном предельном случае минимальное значение $p_{max}$ равно $\frac{1}{n}$, поскольку если бы она была хотя бы немного меньше этого значения, то общая вероятность всех сторон оказалась меньше единицы. Если $p_{max} = \frac{1}{n}$, то ожидаемое количество бросков монеты равно 1. Это тоже логично. Если $p_{max} = \frac{1}{n}$, тогда каждая сторона имеет одинаковую вероятность быть выбранной (а именно $\frac{1}{n}$), поэтому когда мы нормализуем вероятности каждой грани до 1, то каждая грань будет иметь вероятность быть выбранной, равную 1. Поэтому бросок кости для выбора монеты по сути будет определять результат, поскольку монета всегда выпадает орлом, и нам никогда не придётся повторяться.

Интересно, что ожидаемое количество бросков монеты зависит исключительно от значения $p_{max}$, а не от других задействованных вероятностей, но если мы вернёмся к нашему графическому представлению, то это имеет смысл. Общая площадь прямоугольника, в который мы стреляем дротиками, всегда равна $n$, потому что мы нормализовали высоты, сделав их равными 1. Более того, общая площадь, занимаемая прямоугольниками «да» задаётся как $\frac{1}{p_{max}}$, поскольку каждый прямоугольник имеет ширину 1, а высота нормализована умножением на $\frac{1}{p_{max}}$. Это значит, что соотношение общей площади прямоугольников «да» к общей площади всего прямоугольника равна $\frac{1}{n \cdot p_{max}}$. Другими словами, пространство, занимаемое прямоугольниками «нет», зависит только от значения $p_{max}$. Его можно переносить или распределять как угодно, но в результате площадь всегда остаётся одинаковой, и шансы на попадание в неё дротика независимы от положения.

Сравнение этого алгоритма с другими даёт нам следующую информацию:

Алгоритм Время инициализации Время генерации Занятая память
Наилучшее Наихудшее Наилучшее Наихудшее Наилучшая Наихудшая
Шулерская кость из честной кости $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$ $\Theta(1)$ $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$
Шулерская кость из несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ $\Theta(n)$
Выбор колесом рулетки $\Theta(n)$ $\Theta(\log n)$ $\Theta(n)$
Оптимальный выбор колесом рулетки $O(n^2)$ $\Theta(1)$ $O(\log n)$ $\Theta(n)$
Шулерская кость из честных костей/несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ (ожидаемое) $\Theta(n)$

В наилучшем случае этот алгоритм лучше показанного выше алгоритма двоичного поиска, потому что требует всего одного броска монеты. Однако наихудший случай экспоненциально хуже. Можно ли устранить этот наихудший случай?

Alias-метод


Предыдущая техника отлично показывает себя в наилучшем случае, генерируя случайный бросок кости с помощью всего лишь одной честной кости и одной монеты. Но ожидаемое наихудшее поведение намного хуже, и потенциально требует линейного количества бросков кости и монеты. Причина заключается в том, что в отличие от предыдущих техник, алгоритм может «промахиваться» и вынужден повторно выполнять итерации, пока не выберет решение. Графически это можно представить так, что мы бросаем дротики в цель, в которой есть большое количество пустого пространства, не привязанного ни к какому результату. Если бы был какой-то способ устранить всё это пустое пространство таким образом, чтобы каждая часть цели была покрыта прямоугольником, соответствующим какой-то грани шулерской кости, то мы бы просто бросили единственный дротик и считали бы результат.

Хитрый ход мы можем сделать, подстроив высоту прямоугольника таким образом, чтобы она соответствовала не наибольшей вероятности, а средней. Давайте вернёмся к нашему примеру. Вероятности равны $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{12}$, $\frac{1}{12}$. Поскольку у нас четыре вероятности, средняя вероятность должна быть равна $\frac{1}{4}$. Что произойдёт, если мы попытаемся нормализировать высоту прямоугольника по средней вероятности $\frac{1}{4}$, а не максимальной $\frac{1}{2}$? Давайте посмотрим, что получится. Мы начинаем с прямоугольников шириной $1$, высоты которых равны изначальны вероятностям:


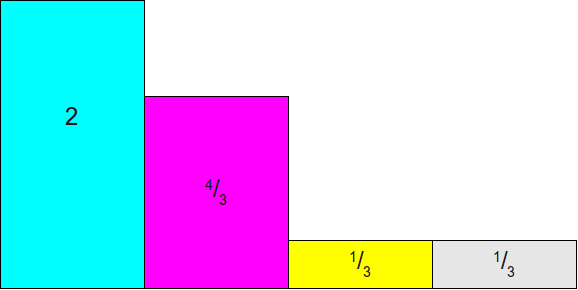
Теперь мы отмасштабируем все эти прямоугольники так, чтобы вероятность $\frac{1}{4}$ имела высоту 1. Этого можно добиться, умножив каждую вероятность на четыре, что даст нам следующую схему:


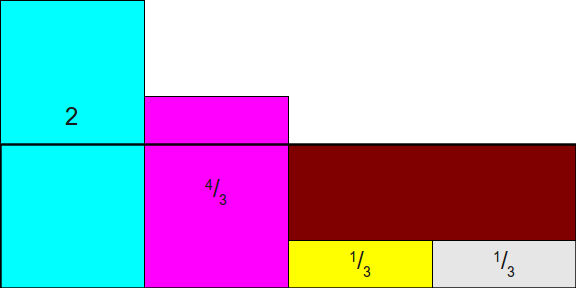
На этом этапе давайте нарисуем поверх этого изображения прямоугольник $1 \times 4$. Он будет обозначать цель, в которую мы стреляем:


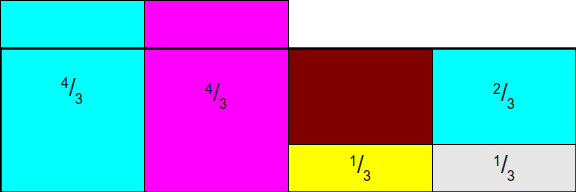
Как видите, это не совсем правильно, потому что прямоугольники для $\frac{1}{2}$ и $\frac{1}{3}$ не помещаются идеально в ограничивающий прямоугольник. Но что если мы разрешим себе разрезать прямоугольники на меньшие куски? То есть что будет, если мы отрежем часть пространства прямоугольника $\frac{1}{2}$ и переместим его в пустое пространство над пространством одного из прямоугольников $\frac{1}{12}$? Мы получим следующую схему, в которой по-прежнему есть нависающие сверху вертикальные полосы, но теперь их уже не так много:


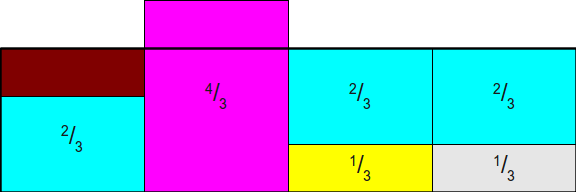
Итак, у нас остались лишние полосы, но их уже не очень много. Мы могли бы полностью устранить лишнее, переместив выделяющиеся части из полос $\frac{1}{2}$ и $\frac{1}{3}$ в пустое пространство, но на самом есть решение получше. Начнём с перемещения $\frac{1}{2}$ полосы из первого столбца в третий, чтобы полностью заполнить оставшийся пробел. У нас появится небольшой пробел в первом столбце, но мы закроем другой пробел:


Наконец, мы перетащим лишнее из второго столбца в первый, получив готовый прямоугольник:


Получившаяся схема обладает замечательными свойствами. Во-первых, общие площади прямоугольников. обозначающих каждую грань шулерской кости, не изменились по сравнению с исходной схемой; мы просто разрезали эти прямоугольники на части и переместили их. Это означает, что пока площади исходных прямоугольников пропорционально распределены согласно исходному распределению вероятностей, то общая площадь каждой грани кости остаётся той же. Во-вторых, заметьте, что в этом новом прямоугольнике нет свободного места, то есть при любом броске дротика мы гарантировано куда-нибудь попадём и получим окончательный ответ, а не пустое пространство, требующее ещё одного броска. Это значит, что единственного броска дротика будет достаточно для генерирования нашего случайного значения. Последнее и самое важное — заметьте, что в каждом столбце содержится не более двух разных прямоугольников. Это значит, что можно воспользоваться предыдущим изобретением — мы бросаем кость, чтобы выбрать несимметричную монету, а затем бросаем монету. Отличие на этот раз заключается в том, что означает бросок монеты. Выпавший орёл означает, что мы выбираем одну грань кости, а выпавшая решка теперь означает, что мы должны выбрать какую-то другую грань кости (а не бросать кость заново).

На высоком уровне alias-метод работает следующим образом. Во-первых, мы создаём прямоугольники, обозначающие каждую из разных вероятностей граней кости. Далее мы разрезаем эти прямоугольники на части и перераспределяем их таким образом, чтобы они полностью заполняли прямоугольную цель, чтобы при этом каждый столбец имел постоянную ширину и содержал прямоугольники максимум двух разных сторон шулерской кости. Наконец, мы симулируем броски кости, случайным образом метая дротик в цель, что можно реализовать сочетанием честной кости и несимметричных монет.

Но как нам узнать, возможно ли вообще разрезать исходные прямоугольники таким образом, чтобы каждый столбец содержал не более двух разных вероятностей? Это не кажется очевидным, но удивительно, что этого действительно можно добиться всегда. Более того, мы не только можем разрезать прямоугольники на части таким образом, что каждый столбец содержит не более двух разных прямоугольников, но и сделать так, чтобы один из прямоугольников в каждом столбце был прямоугольником, изначально расположенным в этом столбце. Можно заметить, что в показанной выше схеме прямоугольников мы всегда вырезали часть прямоугольника и перемещали его в другой столбец и никогда не убирали прямоугольник их исходного столбца полностью. Это означает, что каждый столбец в готовой схеме будет состоять из какого-то прямоугольника, соответствующего вероятности, изначально назначенной этому столбцу, плюс (не обязательно) из второго прямоугольника, перетащенного из какого-то другого столбца. Такой второй прямоугольник часто называют псевдонимом (alias) столбца, потому что оставшаяся вероятность столбца используется в качестве «псевдонима» какой-то другой вероятности. Из-за использования термина «alias» этот метод получил название «alias-метод».

Прежде чем мы перейдём к доказательству того, что можно всегда распределить вероятности таким образом, давайте вкратце опишем суть работы алгоритма. Поскольку каждый столбец готовой схемы всегда содержит какую-то часть исходного прямоугольника из этого столбца (потенциально с нулевой высотой!), то для хранения (потенциально) двух различных прямоугольников, занимающих столбец, реализации alias-метода обычно хранят две разные таблицы: таблицу вероятностей $Prob$ и таблицу alias $Alias$. Обе эти таблицы имеют размер $n$. В таблице вероятностей для каждого столбца хранится вероятность выбора внутри этого столбца исходного прямоугольника, а в таблице alias хранится идентификатор второго прямоугольника, содержащегося в этом столбце (если он есть). Таким образом, генерацию случайного броска кости можно реализовать следующим образом. Во-первых мы с помощью честной кости равномерно случайно выбираем какой-то столбец $i$. Далее бросаем случайную монету с вероятностью выпадения орла $Prob[i]$. Если на монете выпал орёл, то мы возвращаем, что на кости выпала грань $i$, в противном случае возвращаем, что на кости выпала грань $Alias[i]$. Вот пример таблиц вероятностей и alias для использованной выше конфигурации:


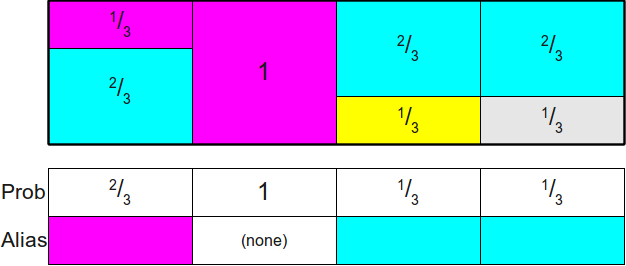
Доказательство существования таблиц Alias


Теперь нам нужно формально доказать, что возможность создания таблиц $Alias$ и $Prob$ существует всегда. Чтобы доказать, что это возможно всегда, нам нужно показать что всегда возможно сделать следующее:

  • Создать прямоугольники $(n \cdot p_i) \times 1$ для каждой из вероятностей $p_i$,
  • разрезать их горизонтально на меньшие части и
  • распределить их на $n$ столбцов
    • так, что высота каждого столбца равна $1$,
    • ни в одном столбце нет больше двух прямоугольников и
    • прямоугольник, соответствующий грани $i$, расположен в столбце $i$.

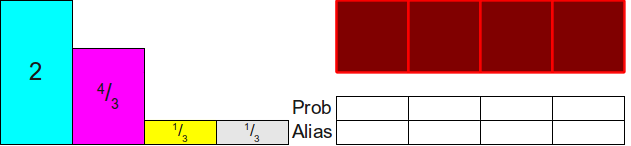
Прежде чем переходить к доказательствам того, что это возможно всегда, давайте рассмотрим пример. Допустим, у нас есть четыре вероятности $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{12}$, $\frac{1}{12}$. Это набор из четырёх вероятностей ($k = n = 4$), сумма которых равна $1 = \frac{4}{4}$. Хотя выше мы экспериментально показали, как заполнить таблицу alias, теперь давайте рассмотрим её создание подробнее и начнём с совершенно пустой таблицы, а затем начнём её заполнять. Мы начинаем с того, что масштабируем все эти вероятности на коэффициент 4, что даёт нам такие вероятности и такую пустую таблицу:


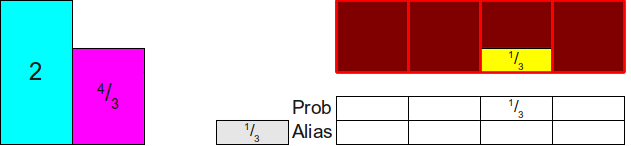
Заметьте, что два из четырёх прямоугольников, которые нам нужно распределить ($\frac{1}{3}$, $\frac{1}{3}$) меньше 1. Это значит, что они не смогут полностью заполнить столбец и для заполнения остатка нам нужна какая-то другая вероятность. Давайте возьмём одну из двух (допустим жёлтую) и поместим её в соответствующий столбец:


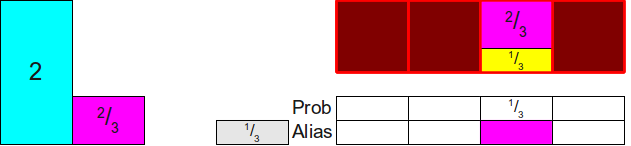
Теперь нам нужно каким-то образом покрыть разность в верхней части столбца. Для этого мы заметим, что два прямоугольника, которые пока не распределены, имеют высоту больше 1 (а именно $2$ и $\frac{4}{3}$). Давайте выберем один из них произвольным образом; пусть это будет $\frac{4}{3}$. Затем мы распределим достаточную часть от $\frac{4}{3}$ в столбец, чтобы полностью заполнить его; в результате мы задействуем $\frac{2}{3}$ из $\frac{4}{3}$, как показан ниже:


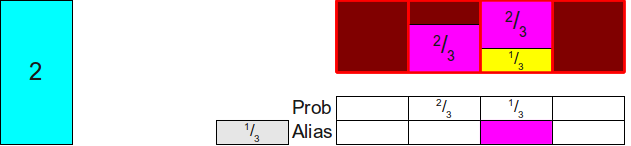
Теперь посмотрим, на что похожа наша схема. У нас есть три прямоугольника, общая площадь которых равна $3$, и три свободных столбца, то есть похоже, что можно распределить эти прямоугольники по этим трём столбцам. Для этого мы воспользуемся тем же трюком, что и ранее. Заметьте, что есть по крайней мере один прямоугольник, высота которого меньше $1$, поэтому мы выберем один из произвольным образом (допустим, прямоугольник $\frac{2}{3}$) и поместим его в свой столбец:


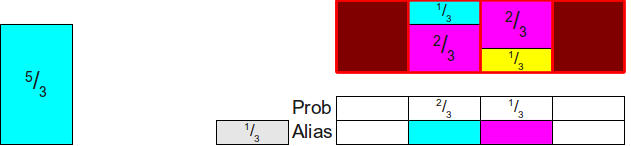
Теперь нам нужно заполнить столбец до конца, поэтому мы возьмём какую-нибудь вероятность, которая не меньше 1, и используем её для дополнения оставшейся части столбца. Здесь у нас есть только один вариант (использовать $2$), поэтому мы забираем $\frac{1}{3}$ из $2$ и помещаем в верхнюю часть столбца:


Теперь всё свелось к двум прямоугольникам, общая площадь которых равна двум. Мы повторяем этот процесс, найдя какой-нибудь прямоугольник, высота которого не больше 1 (здесь это $\frac{1}{3}$), и помещая его в этот столбец:


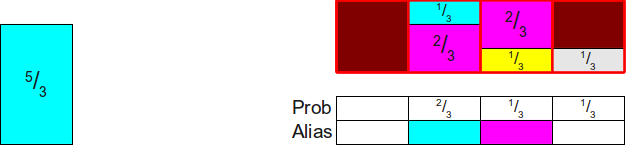
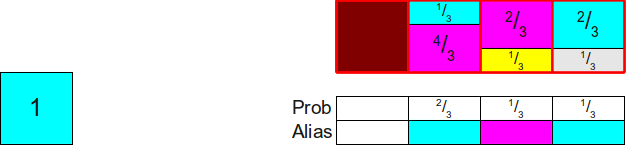
Теперь мы найдём какой-нибудь прямоугольник высотой не менее $1$, чтобы дополнить столбец. Единственный вариант для нас — это $\frac{5}{3}$:


Теперь у нас остался только один прямоугольник, и его площадь равна 1. Поэтому мы можем просто завершить создание, поместив этот прямоугольник в его собственный столбец:


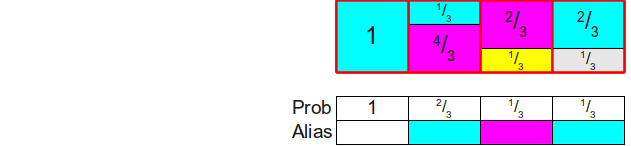
И вуаля! Мы заполнили таблицу.

Заметим, что в основе конструирования этой таблицы лежит общий паттерн:

  • Находим какой-то прямоугольник, высота которого не больше 1, и помещаем его в его собственный столбец, задавая в таблице $Prob$ высоту этого прямоугольника.
  • Находим какой-то прямоугольник, высота которого не меньше 1, используем его для заполнения столбца, задавая в таблице $Alias$ соответствие грани кости, которую представляет этот прямоугольник.

Можно ли доказать, что такое построение в общем случае всегда возможно? То есть что мы не «застрянем», распределяя вероятности таким образом? К счастью, доказательство есть. Можно объяснить это так: мы отмасштабировали все вероятности так, чтобы среднее значение новых вероятностей равнялось 1 (поскольку изначально оно было равно $\frac{1}{n}$, а мы умножили всё на $n$). Мы знаем, что минимум всех отмасштабированных вероятностей должен быть не больше среднего, и что максимум всех отмасштабированных вероятностей должен быть не меньше среднего, поэтому когда мы в первый раз начинаем отсюда, у нас всегда должен быть хотя бы один элемент не больше 1 (а именно наименьшая из всех отмасштабированных вероятностей) и один элемент не меньше 1 (а именно наибольшая из отмасштабированных вероятностей). Следовательно, мы можем соединить эти элементы в пару. Но что произойдёт, если мы уберём их оба? Когда мы это сделаем, то в результате удалим одну вероятность из общей и уменьшим общую сумму отмасштабированных вероятностей на единицу. Это значит, что новое среднее значение не изменилось, потому что средняя отмасштабированная вероятность равна. Мы можем повторять эту процедуру снова и снова, пока в конце концов не соединим в пары все элементы.

Мы можем формализировать это рассуждение в следующей теореме:

Теорема: при наличии $k$ прямоугольников единичной ширины с высотами $h_0$, $h_1$, ..., $h_{k-1}$, такие, что $\sum_{i=0}^{k-1}{h_i} = k$, всегда есть способ разделения прямоугольников и распределения их в $k$ столбцов, каждый из которых имеет высоту 1, таким образом, что каждый столбец будет содержать не более двух разных прямоугольников, и в $i$-том столбце будет содержаться хотя бы одна часть $i$-того прямоугольника.

Доказательство: по индукции. В базовом случае, если $k = 1$, то у нас есть только один прямоугольник и его высота должна быть равна 1. Поэтому мы можем занести его в $0$-ой столбец. Следовательно, каждый столбец имеет высоту 1, содержит не более двух прямоугольников, а в $0$-том столбце содержится не менее одной части $0$-того прямоугольника.

Для этапа индукции предположим, что для какого-то натурального числа $k$ теорема справедлива и рассмотрим любые $k + 1$ прямоугольников шириной $1$ и высотами $h_0$, $h_1$, ..., $h_{k}$, такие, что $\sum_{i = 0}^{k}{h_i} = k + 1$. Сначала мы утверждаем, что существует некая высота $h_l$, такая, что $h_l \le 1$, и какая-то другая высота $h_g$ (такая, что $l \ne g$), такая, что $h_g \ge 1$. Чтобы убедиться в этом, пойдём от обратного и допустим, что нет такой $h_l$ с $h_l \le 1$; это будет значит, что $h_i > 1$ для всех натуральных чисел $i$ в интервале $0 \le i \le k$. Но тогда у нас получится, что $k + 1 = \sum_{i = 0}^k{h_i} > \sum_{i=0}^k{1} = k + 1$, что очевидно невозможно. Следовательно, существует какой-то индекс $l$, такой, что $h_l \le 1$. Теперь снова пойдём от обратного и допустим, что нет никакой другой высоты $h_g$ (с $l \ne g$), такой, что $h_g \ge 1$. Тогда у нас получится, что каждая другая $h_g < 1$, то есть (по аналогичной логике) $\sum_{i=0}^{k}{h_i} < k + 1$ и мы пришли к противоречию. Следовательно, $h_l \le 1$ и $h_g \ge 1$.

Теперь рассмотрим следующую конструкцию. Поместим $h_l$ в столбец $l$ и заполним оставшееся пространство $1 - h_l$ в $l$-том столбце частью прямоугольника $h_g$ (такое пространство должно существовать, поскольку $0 \le 1 - h_l \le 1$ и $h_g \ge 1$). Так мы полностью заполним столбец. Теперь у нас остался набор из $k$ разных частей прямоугольников, чья общая сумма равна $k$, поскольку мы убрали из прямоугольников общую площадь $1$, а изначальная общая сумма была равна $k + 1$. Более того, мы полностью заполнили столбец $l$, то есть нам больше не понадобится размещать там другие части прямоугольников. Следовательно, по индуктивной гипотезе, мы можем распределить оставшиеся $k$ в $k$ столбцов так, чтобы это удовлетворяло приведённым выше условиям. В сочетании с тем фактом, что мы теперь заполнили столбец $l$, это означает, что у нас есть способ заполнения всех столбцов, чтобы это удовлетворяло ограничениям. На этом индукция завершена.

Это доказательство возможности построения, гласящее, что мы не только всегда можем построить таблицу alias, но и то, что приведённый выше алгоритм поиска высоты не больше единицы и соединение её в пару с прямоугольником высотой не меньше единицы всегда оказывается успешным. Из этого мы можем начать выводить всё более и более сложные алгоритмы вычисления таблиц alias.

Генерирование таблиц Alias


Используя сказанное выше, мы можем получить достаточно хороший алгоритм для симуляции бросков шулерской кости с помощью alias-метода. Инициализация заключается в повторяющемся сканировании входящих вероятностей для нахождения значения не больше 1 и значения не меньше 1, с последующим объединением их в пару для заполнения столбца:

Алгоритм: наивный Alias-метод


  • Инициализация:
    1. Умножаем каждую вероятность $p_i$ на $n$.
    2. Создаём массивы $Alias$ и $Prob$, каждый из которых имеет размер $n$.
    3. For $j = 1 \mbox{ to } n - 1$:
      1. Находим вероятность $p_l$, удовлетворяющую условию $p_l \le 1$.
      2. Находим вероятность $p_g$ (с $l \ne g$), удовлетворяющую условию $p_g \ge 1$
      3. Задаём $Prob[l] = p_l$.
      4. Задаём $Alias[l] = g$.
      5. Удаляем $p_l$ из списка изначальных вероятностей.
      6. Задаём $p_g := p_g - (1 - p_l)$.

    4. Пусть $i$ будет последней оставшейся вероятностью, которая должна иметь высоту 1.
    5. Задаём $Prob[i] = 1$.

  • Генерация:
    1. Генерируем бросок честной кости из $n$-гранной кости; называем грань $i$.
    2. Бросаем несимметричную монету, выпадающую орлом с вероятностью $Prob[i]$.
    3. Если на монете выпадает орёл, возвращаем $i$.
    4. В противном случае возвращаем $Alias[i]$.

Этап генерации этого алгоритма точной такой же, как описанный выше метод, и выполняется за время $\Theta(1)$. Этап инициализации требует описанных выше множественных итераций. Во-первых, нам нужно потратить время $\Theta(n)$ на масштабирование каждой вероятности на коэффициент $n$, и потратить время $O(n)$ на выделение двух массивов. Внутренний цикл выполняется $\Theta(n)$ раз, и при каждой итерации выполняет работу $O(n)$ по сканированию массива, удалению одного из элементов массива и обновлению вероятностей. Это даёт нам время $O(n^2)$ общей инициализации. Если мы рассмотрим этот алгоритм в контексте, то у нас получится следующее:

Алгоритм Время инициализации Время генерации Занятая память
Наилучшее Наихудшее Наилучшее Наихудшее Наилучшая Наихудшая
Шулерская кость из честной кости $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$ $\Theta(1)$ $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$
Шулерская кость из несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ $\Theta(n)$
Выбор колесом рулетки $\Theta(n)$ $\Theta(\log n)$ $\Theta(n)$
Оптимальный выбор колесом рулетки $O(n^2)$ $\Theta(1)$ $O(\log n)$ $\Theta(n)$
Шулерская кость из честных костей/несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ (ожидаемое) $\Theta(n)$
Наивный Alias-метод $O(n^2)$ $\Theta(1)$ $\Theta(n)$

По сравнению с другими эффективными методами симуляции этот наивный alias-метод имеет высокие затраты на инициализацию, но затем может чрезвычайно эффективно симулировать броски кости. Если бы мы могли каким-то образом снизить затраты на инициализацию (допустим, до $O(n)$), то этот метод был бы совершенно точно лучше всех используемых здесь техник.

Один простой способ снижения затрат на инициализацию заключается в использовании более подходящей структуры данных для сохранения высот в процессе выполнения. В наивной версии мы используем для хранения всех вероятностей неотсортированный массив, то есть для нахождения двух нужных вероятностей требуется время $O(n)$. Более подходящей альтернативой для хранения значений будет сбалансированное двоичное дерево поиска. В этом случае мы сможем находить значения $p_g$ и $p_l$ за время $O(\log n)$, выполняя поиск максимального и минимального значений дерева. Удаление $p_l$ можно выполнять за время $O(\log n)$, а обновление вероятности $p_g$ тоже может выполняться за $O(\log n)$ благодаря простому удалению её из дерева с последующей повторной вставкой. Это даёт нам следующий алгоритм:

Алгоритм: Alias-метод


  • Инициализация:
    1. Создаём массивы $Alias$ и $Prob$, каждый размером $n$.
    2. Создаём сбалансированное двоичное дерево поиска $T$.
    3. Вставляем $n \cdot p_i$ в $T$ для каждой вероятности $i$.
    4. For $j = 1 \mbox{ to } n - 1$:
      1. Находим и удаляем наименьшее значение в $T$; назовём его $p_l$.
      2. Находим и удаляем наибольшее значение в $T$; назовём его $p_g$.
      3. Задаём $Prob[l] = p_l$.
      4. Задаём $Alias[l] = g$.
      5. Задаём $p_g := p_g - (1 - p_l)$.
      6. Добавляем $p_g$ к $T$.

    5. Пусть $i$ будет последней оставшейся вероятностью, которая должна иметь вес 1.
    6. Задаём $Prob[i] = 1$.

  • Генерация:
    1. Генерируем бросок честной кости из $n$-гранной кости; называем грань $i$.
    2. Бросаем несимметричную монету, на которой выпадает орёл с вероятностью $Prob[i]$.
    3. Если на монете выпадает орёл, возвращаем $i$.
    4. В противном случае возвращаем $Alias[i]$.

Теперь инициализация нашего алгоритма происходит гораздо быстрее. Создание $Alias$ и $Prob$ по-прежнему занимает время $O(n)$ на каждую таблицу, а добавление вероятностей в BST $T$ занимает время $\Theta(n \log n)$. Далее мы выполняем $\Theta(n)$ итераций по заполнению таблицы, каждая из которых занимает время $O(\log n)$. Это даём нам общее время инициализации $O(n \log n)$:

Алгоритм Время инициализации Время генерации Занятая память
Наилучшее Наихудшее Наилучшее Наихудшее Наилучшая Наихудшая
Шулерская кость из честной кости $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$ $\Theta(1)$ $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$
Шулерская кость из несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ $\Theta(n)$
Выбор колесом рулетки $\Theta(n)$ $\Theta(\log n)$ $\Theta(n)$
Оптимальный выбор колесом рулетки $O(n^2)$ $\Theta(1)$ $O(\log n)$ $\Theta(n)$
Шулерская кость из честных костей/несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ (ожидаемое) $\Theta(n)$
Наивный Alias-метод $O(n^2)$ $\Theta(1)$ $\Theta(n)$
Alias-метод $O(n \log n)$ $\Theta(1)$ $\Theta(n)$

Однако существует алгоритм, работающий ещё быстрее. Он на удивление прост, и, вероятно, является наиболее чистым из алгоритмов реализации alias-метода. Этот алгоритм впервые описан в статье «A Linear Algorithm For Generating Random Numbers With a Given Distribution» Майкла Воуза, и стал стандартным алгоритмом реализации alias-метода.

В основе алгоритма Воуза лежит использование двух рабочих списков: один содержит элементы с высотой меньше 1, другой содержит элементы с высотой не меньше 1. Алгоритм постоянно соединяет парами первые элементы каждого рабочего списка. На каждой итерации мы потребляем элемент из списка «малых» значений, и потенциально перемещаем остаток элемента из списка «больших» значений в список «малых». В этом алгоритме используется несколько инвариантов:

  • Все элементы «малого» рабочего списка меньше 1.
  • Все элементы «большого» рабочего списка не меньше 1.
  • Сумма элементов в рабочих списка всегда равна общему количеству элементов.

Для упрощения каждый список хранит не саму вероятность, а некий указатель на список исходных вероятностей, сообщающий, на какую грань шулерской кости выполняется ссылка. Имея эти инварианты, мы получаем следующий алгоритм:

Алгоритм: (нестабильный) Alias-метод Воуза


Предупреждение: этот алгоритм подвержен численным неточностям. Более численно стабильный алгоритм представлен ниже.


  • Инициализация:
    1. Создаём массивы $Alias$ и $Prob$, каждый размером $n$.
    2. Создаём два рабочих списка, $Small$ и $Large$.
    3. Умножаем каждую вероятность на $n$.
    4. Для каждой отмасштабированной вероятности $p_i$:
      1. Если $p_i < 1$, добавляем $i$ к $Small$.
      2. В противном случае ($p_i \ge 1$) добавляем $i$ к $Large$.

    5. Пока список $Small$ не пуст:
      1. Удаляем первый элемент из $Small$; называем его $l$.
      2. Удаляем первый элемент из $Large$; называем его $g$.
      3. Задаём $Prob[l] = p_l$.
      4. Задаём $Alias[l] = g$.
      5. Задаём $p_g := p_g - (1 - p_l)$.
      6. Если $p_g < 1$, добавляем $g$ в $Small$.
      7. В противном случае ($p_g \ge 1$) добавляем $g$ в $Large$.

    6. Пока список $Large$ не пуст:
      1. Удаляем первый элемент из $Large$; называем его $g$.
      2. Задаём $Prob[g] = 1$.


  • Генерация:
    1. Генерируем бросок честной кости из $n$-гранной кости; называем грань $i$.
    2. Бросаем несимметричную монету, на которой выпадает орёл с вероятностью $Prob[i]$.
    3. Если на монете выпадает орёл, возвращаем $i$.
    4. В противном случае возвращаем $Alias[i]$.

С учётом трёх представленных выше инвариантов первая часть алгоритма (всё, за исключением последнего цикла) должна быть достаточно понятна: мы постоянно соединяем в пары какой-то малый элемент из $Small$ с большим элементом из $Large$, а затем добавляем остаток большого элемента в соответствующий рабочий список. Последний цикл алгоритма требует объяснений. После исчерпания всех элементов в списке $Small$ в списке $Large$ останется не менее одного элемента (поскольку если каждый элемент находился $Small$, то сумма элементов должна была стать меньше количества оставшихся элементов, что нарушает условия последнего инварианта). Поскольку каждый элменрт $Large$ не меньше 1, а сумма $k$ элементов в $Large$ должна быть равна $k$, то каждый элемент в $Large$ должен быть равен 1, потому что в противном случае общая сумма будет слишком большой. Поэтому этот последний цикл присваивает вероятности каждого большого элемента значение 1, чтобы все столбцы, содержащие большой элемент, были равны 1.

В этом алгоритме тип рабочего списка не важен. В первоначальной статье Воуза в качестве рабочего списка используются стеки, потому что их можно эффективно реализовать с помощью массивов, но если мы захотим, то можем использовать очередь. Однако для простоты мы воспользуемся стеком.

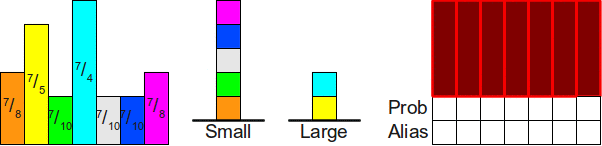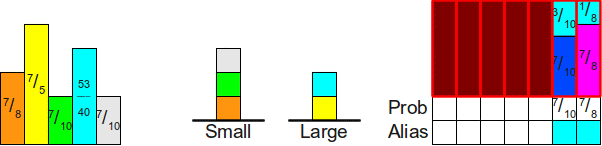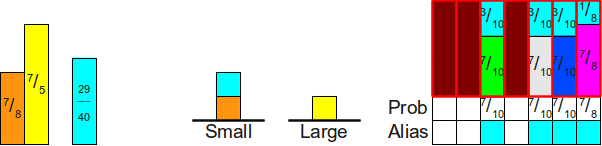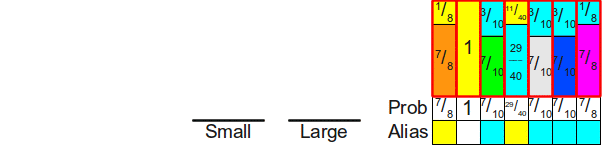
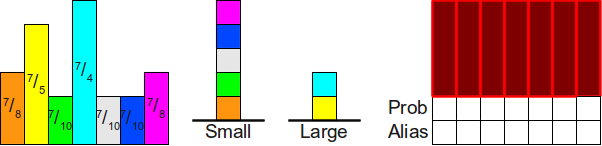
Прежде чем переходить к анализу алгоритма, давайте разберём его работу на примере. Рассмотрим пример с использованием семи вероятностей $\frac{1}{4}$, $\frac{1}{5}$, $\frac{1}{8}$, $\frac{1}{8}$, $\frac{1}{10}$, $\frac{1}{10}$, $\frac{1}{10}$. Чтобы подчеркнуть тот факт, что алгоритм не сортирует вероятности и не требует их сортировки, давайте расположим их в произвольном порядке $\frac{1}{8}$, $\frac{1}{5}$, $\frac{1}{10}$, $\frac{1}{4}$, $\frac{1}{10}$, $\frac{1}{10}$, $\frac{1}{8}$. Алгоритм начинается с добавления этих элементов в два рабочих стека:


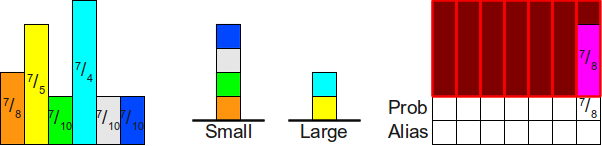
Теперь мы разместим вершину стека $Small$ в его позиции, переместив сиреневый прямоугольник в его конечную позицию:


Теперь мы используем вершину стека $Large$ (бирюзовый прямоугольник) для заполнения оставшейся части столбца. Поскольку $\frac{7}{4} - \frac{1}{8} = \frac{13}{8} \ge 1$, мы оставляем бирюзовый блок на вершине стека $Large$:


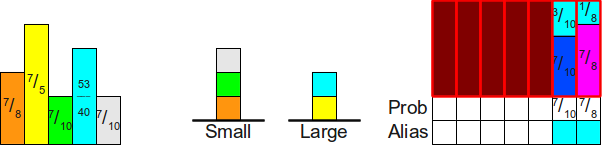
Затем мы повторяем этот процесс. Перемещаем прямоугольник из вершины стека $Small$ в его столбец, а затем дополняем недостающее вершиной стека $Large$:


И ещё раз:


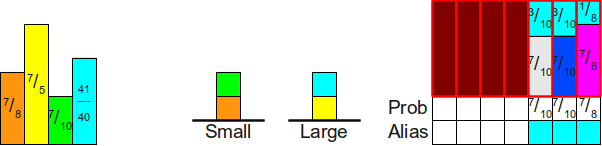
Когда мы повторим этот процесс в следующий раз, то обнаружим, что хотя мы и можем использовать бирюзовый блок для заполнения пустого пространства в таблице, но в результате этого высота бирюзового блока станет меньше единицы. Следовательно, нам нужно будет переместить бирюзовый блок на вершину стека малых значений:


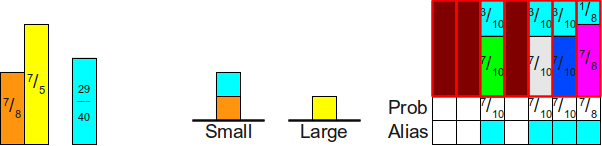
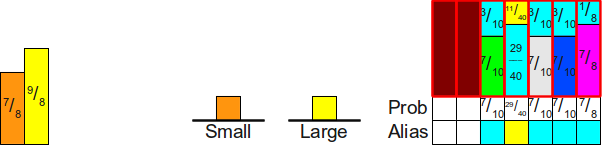
Теперь при обработке списка $Small$ мы помещаем бирюзовый блок на его место, а затем используем жёлтый блок для заполнения стека:


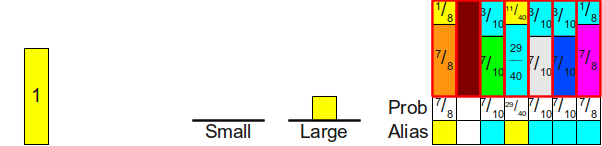
Затем мы обрабатываем стек $Small$, чтобы переместить оранжевый блок в его позицию, заполняя остатки жёлтым блоком:


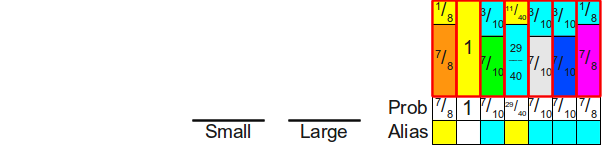
И наконец, поскольку стек $Small$ пуст, мы помещаем жёлтый блок в его столбец и на этом заканчиваем.


И у нас получилась хорошо сформированная таблица alias для этих вероятностей.

Практичная версия алгоритма Воуза


К сожалению, приведённый выше алгоритм в таком виде численно нестабилен. Он вполне точен на идеализированной машине, способной выполнять вычисления с вещественными числами произвольной точности, но если попробовать выполнить его с помощью IEEE-754 double, то он в результате может оказаться совершенно ошибочным. Вот два источника неточностей, с которыми нам нужно разобраться, прежде чем двигаться дальше:

  1. Вычисление того, принадлежит ли вероятность к рабочему списку $Small$ или к $Large$, может быть неточным. В частности, может возникнуть ситуация, в которой масштабирование вероятностей на коэффициент $n$ приводит к том, что вероятности, равные $\frac{1}{n}$, в результате оказываются немного меньше $1$ (то есть попадают в список $Small$, а не в $Large$).
  2. Вычисление, вычитающее соответствующую массу вероятностей из большей вероятности, численно нестабильно и может вносить значительные ошибки округления. Это может приводить к том, что вероятность, которая должна быть в списке $Large$, оказывается в списке $Small$.

Сочетание этих двух факторов означает, что в результате алгоритм может случайно поместить все вероятности в список $Small$ вместо списка $Large$. Поэтому работа алгоритма может завершиться сбоем, ведь он ожидает, что когда список $Small$ не пуст, тогда и список $Large$ не пуст.

К счастью, исправить это оказывается не так сложно. Мы изменим внутренний цикл алгоритма так, чтобы он завершался, когда любой из списков оказывается пустым, чтобы нам случайно не пришлось искать несуществующие элементы в списке $Large$. Во-вторых, когда один список пуст, мы присвоим оставшимся вероятностям элементов другого списка значение $1$, потому что с математической точки зрения это может происходить только тогда, когда все оставшиеся вероятности в точности равны $1$. Наконец, мы заменим обновляющее большие вероятности вычисление на немного более стабильное вычисление. Тогда получим следующее:

Алгоритм: Alias-метод Воуза


  • Инициализация:
    1. Создаём массивы $Alias$ и $Prob$, каждый размером $n$.
    2. Создаём два рабочих списка, $Small$ и $Large$.
    3. Умножаем каждую вероятность на $n$.
    4. Для каждой отмасштабированной вероятности $p_i$:
      1. Если $p_i < 1$, добавляем $i$ в $Small$.
      2. В противном случае ($p_i \ge 1$) добавляем $i$ в $Large$.

    5. Пока $Small$ и $Large$ не пусты: ($Large$ может быть сначала опустошён)
      1. Удаляем первый элемент из $Small$; называем его $l$.
      2. Удаляем первый элемент из $Large$; называем его $g$.
      3. Задаём $Prob[l] = p_l$.
      4. Задаём $Alias[l] = g$.
      5. Задаём $p_g := (p_g + p_l) - 1$. (Это более численно стабильный вариант.)
      6. Если $p_g < 1$, добавляем $g$ в $Small$.
      7. В противном случае ($p_g \ge 1$) добавляем $g$ в $Large$.

    6. Пока $Large$ не пуст:
      1. Удаляем первый элемент из $Large$; называем его $g$.
      2. Задаём $Prob[g] = 1$.

    7. Пока $Small$ не пуст: Это возможно только из-за численной нестабильности.
      1. Удаляем первый элемент из $Small$; называем его $l$.
      2. Задаём $Prob[l] = 1$.


  • Генерация:
    1. Генерируем бросок честной кости из $n$-гранной кости; называем грань $i$.
    2. Бросаем несимметричную монету, на которой выпадает орёл с вероятностью $Prob[i]$.
    3. Если на монете выпадает орёл, возвращаем $i$.
    4. В противном случае возвращаем $Alias[i]$.

Единственное, что нам осталось — проанализировать сложность алгоритма. Создание рабочих списков в общем занимает время $\Theta(n)$, поскольку мы добавляем каждый элемент ровно в один из списков. Внутренний цикл выполняется за время $\Theta(1)$, поскольку ему требуется удалить два элемента из рабочего списка, обновить два массива и добавить один элемент обратно в список. Он не может выполняться больше $O(n)$ раз, поскольку каждая итерация уменьшает количество элементов (суммарное) в списках на единицу, устраняя малую вероятность. Каждый из двух последних циклов могут выполняться не более чем за $O(n)$, поскольку в списках $Large$ и $Small$ содержится не более $O(n)$ элементов. Это даёт нам общее время выполнения $\Theta(n)$, что (как видно) является наилучшим результатом:
Алгоритм Время инициализации Время генерации Занятая память
Наилучшее Наихудшее Наилучшее Наихудшее Наилучшая Наихудшая
Шулерская кость из честной кости $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$ $\Theta(1)$ $\Theta(n)$ $O(\prod_{i = 0}^n{d_i})$
Шулерская кость из несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ $\Theta(n)$
Выбор колесом рулетки $\Theta(n)$ $\Theta(\log n)$ $\Theta(n)$
Оптимальный выбор колесом рулетки $O(n^2)$ $\Theta(1)$ $O(\log n)$ $\Theta(n)$
Шулерская кость из честных костей/несимметричных монет $\Theta(n)$ $\Theta(1)$ $\Theta(n)$ (ожидаемое) $\Theta(n)$
Наивный Alias-метод $O(n^2)$ $\Theta(1)$ $\Theta(n)$
Alias-метод $O(n \log n)$ $\Theta(1)$ $\Theta(n)$
Alias-метод Воуза $\Theta(n)$ $\Theta(1)$ $\Theta(n)$

Мысли в заключение


Ого! Мы проделали большую работу! Исследовали различные методы симуляции шулерской кости, начиная с самого простого набора техник и заканчивая чрезвычайно быстрыми и эффективными алгоритмами. Каждый метод демонстрирует собственный набор техник, и я считаю окончательную версию (alias-метод Воуза) одним из самых интересных и элегантных алгоритмов, с которыми мне когда-либо приходилось встречаться.

Если вам интересно посмотреть код alias-метод Воуза, в том числе краткое описание сложностей, возникающих на практике из-за численной неточности, то у меня есть реализация alias-метода на Java, выложенная в архиве интересного кода.

Надеюсь, статья была вам полезна!
Tags:
Hubs:
If this publication inspired you and you want to support the author, do not hesitate to click on the button
+37
Comments16
1748
Karma
4
Rating
@PatientZero

Переводчик-фрилансер

Send message

Articles

Show the best of all time
Change theme settings

Your account

Sections

Information

Services

Support
© 2006–2024, Habr