Недавно я натолкнулся на вопрос на Stackoverflow, как восстанавливать исходные слова из сокращений: например, из wtrbtl получать water bottle, а из bsktball — basketball. В вопросе было дополнительное усложнение: полного словаря всех возможных исходных слов нет, т.е. алгоритм должен быть в состоянии придумывать новые слова.
Вопрос меня заинтриговал, и я полез разбираться, какие алгоритмы и математика лежат в основе современных опечаточников (spell-checkers). Оказалось, что хороший опечаточник можно собрать из n-граммной языковой модели, модели вероятности искажений слов, и жадного алгоритма поиска по лучу (beam search). Вся конструкция вместе называется модель зашумлённого канала (noisy channel).
Вооружившись этими знаниями и Питоном, я за вечер создал с нуля модельку, способную, обучившись на тексте "Властелина колец" (!), распознавать сокращения вполне современных спортивных терминов.
Опечаточники используются много где: от клавиатуры вашего телефона до поисковых систем и голосовых помощников. Сделать хороший опечаточник не так просто, ибо он должен быть одновременно быстрым и готовым ко всему (в том числе исправить ошибки в словах, которые до этого никогда не видел). Именно поэтому в опечаточниках используется столько науки. Цель статьи — дать представление об этой науке и просто развлечься.
Математика внутри опечаточника
Модель зашумлённого канала рассматривает каждую аббревиатуру как результат случайного искажения исходной фразы.
Чтобы восстановить оригинальное словосочетание, надо ответить на два вопроса: какие исходные слова вероятны, и какие искажения фраз вероятны?
По теореме Байеса,
где — это любое такое изменение исходной
, которое делает из неё наблюдаемую
. Символ
обозначает прямую пропорциональность.
И вероятность всевозможнных фраз, и вероятность трансформаций могут быть оценены с помощью статистических моделей. Я буду использовать простейший вид моделей — буквенные n-граммы. Можно было бы применять и более сложные модели (например, рекуррентные нейросети), принципиально это ничего не меняет.
Имея такие модели, можно подобрать наиболее правдоподобную исходную фразу буква за буквой, используя алгоритм жадного направленного поиска, beam search.
N-граммная языковая модель
n-граммная модель по предыдущим n-1 буквам фразы определяет вероятность следующей, n-той буквы (и игнорирует все буквы, которые были перед ними). Например, вероятность буквы "g" после последовательности "bowlin" будет вычислена 4-граммной моделью как , т.к. все буквы, предшествующие этим четырём, модель для простоты игнорирует. Такие условные вероятности определяются ("выучиваются") по обучающему корпусу текстов. Продолжая пример,
где — это количество сочетаний "ling" в обучающем корпусе, а
— количество всех 4-грамм в тексте, начинающихся на "lin".
Чтобы оценивать вероятности даже редких n-грамм более адекватно, я применил две уловки. Во-первых, к каждому счётчику я прибавляю число — это гарантирует, что я не буду делить на ноль. Во-вторых, для подсчёта я использую не только n-граммы (которых может быть мало в тексте), но и (n-1)-граммы (они встречаются чаще), и так далее, вплоть до самой простой модели, которая вообще не смотрит на контекст. Но счётчики меньших порядков используются с весами, убывающими в геометрической прогрессии с темпом
. Поэтому на самом деле вероятность
я вычисляю как
Впрочем, довольно теории! Посмотрим лучше, как выглядит код модели на языке Python
from collections import defaultdict, Counter
import numpy as np
import pandas as pd
class LanguageNgramModel:
""" Модель запоминает и предсказывает, за какими буквами следуют какие.
Параметры конструктора:
order - порядок (сколько предыдущих букв помнит модель), или n-1
smoothing - величина, добавляемая к каждому счётчику букв для устойчивости
recursive - вес, с которым используется модель на один порядок меньше
Обучаемые параметры:
counter_ - хранилище частот n-грам, в виде словаря счётчиков.
vocabulary_ - множество всех символов, учитываемых моделью
"""
def __init__(self, order=1, smoothing=1.0, recursive=0.001):
self.order = order
self.smoothing = smoothing
self.recursive = recursive
def fit(self, corpus):
""" Оценка числа всех буквосочетаний по тексту
Параметры:
corpus - текстовая строка.
"""
self.counter_ = defaultdict(lambda: Counter())
self.vocabulary_ = set()
for i, token in enumerate(corpus[self.order:]):
context = corpus[i:(i+self.order)]
self.counter_[context][token] += 1
self.vocabulary_.add(token)
self.vocabulary_ = sorted(list(self.vocabulary_))
if self.recursive > 0 and self.order > 0:
self.child_ = LanguageNgramModel(self.order-1, self.smoothing, self.recursive)
self.child_.fit(corpus)
def get_counts(self, context):
""" Оценка частоты всех символов, которые могут следовать за контекстом
Параметры:
context - текстовая строка (учиываются только последние self.order символов)
Возвращает:
freq - вектор условных частот букв, в форме pandas.Series
"""
if self.order:
local = context[-self.order:]
else:
local = ''
freq_dict = self.counter_[local]
freq = pd.Series(index=self.vocabulary_)
for i, token in enumerate(self.vocabulary_):
freq[token] = freq_dict[token] + self.smoothing
if self.recursive > 0 and self.order > 0:
child_freq = self.child_.get_counts(context) * self.recursive
freq += child_freq
return freq
def predict_proba(self, context):
""" Сглаженная оценка вероятности всех символов, которые могут следовать за контекстом
Параметры:
context - текстовая строка (учиываются только последние self.order символов)
Возвращает:
freq - вектор условных вероятностей букв, в форме pandas.Series """
counts = self.get_counts(context)
return counts / counts.sum()
def single_log_proba(self, context, continuation):
""" Оценка логарифма вероятности конкретного продолжения данной фразы.
Параметры:
context - текстовая строка, известное начало фразы
continuation - текстовая строка, гипотетическое продолжение фразы
"""
result = 0.0
for token in continuation:
result += np.log(self.predict_proba(context)[token])
context += token
return result
def single_proba(self, context, continuation):
""" Оценка вероятности конкретного продолжения данной фразы.
Параметры:
context - текстовая строка, известное начало фразы
continuation - текстовая строка, гипотетическое продолжение фразы
"""
return np.exp(self.single_log_proba(context, continuation))Модель "опечаток"
Языковая модель была нужна, чтобы понять, какими обычно бывают исходные фразы. Модель искажений нужна, чтобы понять, как обычно исходные фразы искажаются.
Я буду предполагать, что единственное возможное искажение — это вычёркивание из фразы некоторых символов. При желании, модель можно модифицировать, чтобы она учитывала и другие искажения, например, замены и перестановки букв.
У меня нет большой выборки, на которой можно обучать сложную модель. Поэтому для оценки вероятности искажений я буду использовать 1-граммы. То есть моя модель будет просто запоминать для каждого символа, с какой вероятностью он вычёркивается из сокращения. Впрочем, закодирую я её на всякий случай в общем виде, как n-граммную модель.
class MissingLetterModel:
""" Модель запоминает и предсказывает, какие буквы обычно исключаются из сокращений
Параметры:
order - порядок, или n+1
smoothing_missed - число, прибавляемое к счётчику пропущенных символов
smoothing_total - число, прибавляемое к счётчику всех символов
"""
def __init__(self, order=0, smoothing_missed=0.3, smoothing_total=1.0):
self.order = order
self.smoothing_missed = smoothing_missed
self.smoothing_total = smoothing_total
def fit(self, sentence_pairs):
""" Оценка частоты сокращения символов на основе обучающих примеров
Параметры:
sentence_pairs - список пар (исходная фраза, сокращение)
В сокращении все пропущенные символы заменены на дефисы.
"""
self.missed_counter_ = defaultdict(lambda: Counter())
self.total_counter_ = defaultdict(lambda: Counter())
for (original, observed) in sentence_pairs:
for i, (original_letter, observed_letter) in enumerate(zip(original[self.order:], observed[self.order:])):
context = original[i:(i+self.order)]
if observed_letter == '-':
self.missed_counter_[context][original_letter] += 1
self.total_counter_[context][original_letter] += 1
def predict_proba(self, context, last_letter):
""" Оценка вероятности того, что символ last_letter пропущен после символов context"""
if self.order:
local = context[-self.order:]
else:
local = ''
missed_freq = self.missed_counter_[local][last_letter] + self.smoothing_missed
total_freq = self.total_counter_[local][last_letter] + self.smoothing_total
return missed_freq / total_freq
def single_log_proba(self, context, continuation, actual=None):
""" Оценка логарифма вероятности того, после фразы context фраза continuation трансформируется в actual
Если actual не указана, предполагается, что continuation не изменяется.
"""
if not actual:
actual = continuation
result = 0.0
for orig_token, act_token in zip(continuation, actual):
pp = self.predict_proba(context, orig_token)
if act_token != '-':
pp = 1 - pp
result += np.log(pp)
context += orig_token
return result
def single_proba(self, context, continuation, actual=None):
""" Оценка вероятности того, после фразы context фраза continuation трансформируется в actual
Если actual не указана, предполагается, что continuation не изменяется.
"""
return np.exp(self.single_log_proba(context, continuation, actual))Пример работы моделей
Чтобы понять, как работают модели языка и сокращений, посмотрим на простой пример. Языковая модель обучим на одном слове и посмотрим, как она предсказывает продолжение слова "bra". С её точки зрения, "b" — самое правдоподобное продолжение (потому что эта буква чаще всего идёт после "a").
lang_model = LanguageNgramModel(1)
lang_model.fit(' abracadabra ')
print(lang_model.predict_proba(' bra')) 0.181777
a 0.091297
b 0.272529
c 0.181686
d 0.181686
r 0.091025
dtype: float64Модель сокращений обучим тоже на одном примере (слово, сокращение). В этом примере мы сокращали только букву "а", поэтому для неё вероятность сокращения модель оценивает высоко, а для буквы "b" — ниже. Вероятность пропуска буквы "c" модель оценила выше, чем "b", потому что "с" она реже встречала в обучающих примерах.
missed_model = MissingLetterModel(0)
missed_model.fit([('abracadabra', 'abr-c-d-br-')])
print({letter: missed_model.predict_proba('abr', letter) for letter in 'abc'}){'a': 0.7166666666666667, 'b': 0.09999999999999999, 'c': 0.15}А вот так модель сокращений оценивает вероятность того, что "abra" будет сокращена как "abr-"
print(missed_model.single_proba('', 'abra', 'abr-'))0.164475Жадный поиск наиболее правдоподобной фразы
Имея модели языка и искажений, теоретически можно оценить вероятность любой исходной фразы. Для этого нужно всего лишь перебрать все возможные пары (исходная фраза, трансформация) и оценить правдоподобие каждой. Но их слишком много: например, в алфавите из 27 символов возможны фраз из 10 букв; перебрать их все — нереально. Нужен более хитрый алгоритм.
Мы воспользуемся тем, что обе модели — однобуквенные, и будем подбирать буквы исходной фразы одну за другой. Для этого мы заведём кучу неполных фраз-кандидатов, и для каждой оценим, насколько она соответствует аббревиатуре. Наилучшего кандидата мы дополним всеми разнообразными буквами-продолжениями и гипотезами о том, были ли они пропущены, и добавим в кучу. Чтобы не создавать слишком много вариантов, будем брать только "достаточно хорошие" продолжения. Тех кандидатов, которые уже могут быть полноценными исходными фразами, мы отложим в сторону, и в конце выдадим в качестве ответа. Процедуру будем повторять, пока не закончится куча либо максимальное число итераций.
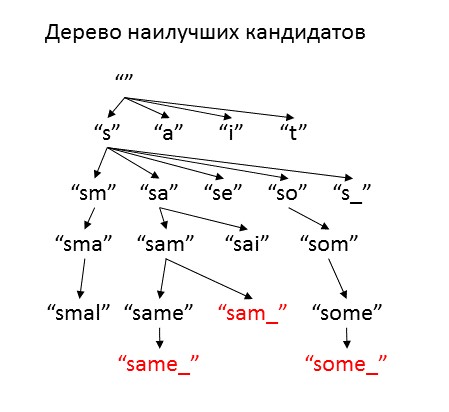
Как меру качества кандидатов мы будем использовать оценку логарифма вероятности имеющейся аббревиатуры при условии того, что исходная фраза начинается, как этот кандидат, а заканчивается, как сама аббревиатура. Для управления поиском введём два параметра — optimism и freedom. Optimism оценивает, насколько улучшится расшифровка, когда мы дойдём до конца аббревиатуры. Этот коэффициент имеет смысл выбирать между 0 и 1, и чем ближе он к 1, тем быстрее алгоритм будет пытаться добавить новые символы в расшифровку. Freedom — это то, насколько качество кандидатов может быть хуже наилучшего текущего варианта, и при увеличении этого параметра алгоритм рассматривает больше различных вариантов. Если установить очень высокое значение freedom, алгоритм будет перебирать все варианты (коих бесконечность), и работать очень долго, но при маленьких значениях freedom куча может закончиться до того, как будет найден хоть один адекватный вариант.
from heapq import heappush, heappop
def generate_options(prefix_proba, prefix, suffix, lang_model, missed_model, optimism=0.5, cache=None):
""" Генерация вариантов расшифровки аббревиатуры (вспомогательная функция)
Параметры:
prefix_proba - правдоподобие расшифрованной части аббревиатуры
prefix - расшифрованная часть аббревиатуры
suffix - не расшифрованная часть аббревиатуры
lang_model - модель языка
missed_model - модель вероятности сокращений
optimism - коэффициент, с которым учитывается не объясненный конец слова
cache - хранилище оценок качества концов слова
Возвращает: список опций в форме (оценка качества, расшифрованная часть,
не расшифрованная часть, новая буква, оценка качества не расшифрованной части)
"""
options = []
for letter in lang_model.vocabulary_ + ['']:
if letter: # тут мы считаем, что буква была пропущена
next_letter = letter
new_suffix = suffix
new_prefix = prefix + next_letter
proba_missing_state = - np.log(missed_model.predict_proba(prefix, letter))
else: # тут мы считаем, что пропущенной буквы не было
next_letter = suffix[0]
new_suffix = suffix[1:]
new_prefix = prefix + next_letter
proba_missing_state = - np.log((1 - missed_model.predict_proba(prefix, next_letter)))
proba_next_letter = - np.log(lang_model.single_proba(prefix, next_letter))
if cache:
proba_suffix = cache[len(new_suffix)] * optimism
else:
proba_suffix = - np.log(lang_model.single_proba(new_prefix, new_suffix)) * optimism
proba = prefix_proba + proba_next_letter + proba_missing_state + proba_suffix
options.append((proba, new_prefix, new_suffix, letter, proba_suffix))
return optionsЕсли внимательно почитать мой код, можно заметить, что я сделал ещё одно упрощение — вместо того, чтобы суммировать вероятности всех искажений исходного слова, я рассматриваю только одно искажение. Это не всегда верно: например, "ball" можно сократить до "bl", вычеркнув как первую ("b--l"), так и вторую ("b-l-") букву "l". Но если таких повторений нет, то адекватный вариант сокращения почти всегда единственный.
def noisy_channel(word, lang_model, missed_model, freedom=3.0, max_attempts=10000, optimism=0.9, verbose=False):
""" Подбор фраз, аббревиатурой которых может быть word
Параметры:
word - аббревиатура
lang_model - модель языка
missed_model - модель вероятности сокращений
freedom - возможный зазор по оценке логарифма правдоподобия кандидатов
max_attempts - число итераций
optimism - коэффициент, с которым учитывается не объясненный конец слова
verbose - печатать ли наилучших текущих кандидатов в ходе исполнения функции
Возвращает: словарик с ключами - расшифровками
и значениями - минус логарифмом правдоподобия расшифровок.
Чем меньше значение, тем правдоподобнее расшифровка.
"""
query = word + ' '
prefix = ' '
prefix_proba = 0.0
suffix = query
full_origin_logprob = -lang_model.single_log_proba(prefix, query)
no_missing_logprob = -missed_model.single_log_proba(prefix, query)
best_logprob = full_origin_logprob + no_missing_logprob
# добавляем в кучу пустое начало
heap = [(best_logprob * optimism, prefix, suffix, '', best_logprob * optimism)]
# добавляем в кандидаты расшифровку по умолчанию - без пропущенных букв
candidates = [(best_logprob, prefix + query, '', None, 0.0)]
if verbose:
print('baseline score is', best_logprob)
# готовим хранилище вероятностей конфов слов
cache = {}
for i in range(len(query)+1):
future_suffix = query[:i]
cache[len(future_suffix)] = -lang_model.single_log_proba('', future_suffix) # rough approximation
cache[len(future_suffix)] += -missed_model.single_log_proba('', future_suffix) # at least add missingness
for i in range(max_attempts):
if not heap:
break
next_best = heappop(heap)
if verbose:
print(next_best)
if next_best[2] == '': # слово расшифровано до конца
# если оно достаточно хорошее, добавим его в кандидаты
if next_best[0] <= best_logprob + freedom:
candidates.append(next_best)
# обновим наилучшую оценку правдоподобия
if next_best[0] < best_logprob:
best_logprob = next_best[0]
else: # it is not a leaf - generate more options
prefix_proba = next_best[0] - next_best[4] # all proba estimate minus suffix
prefix = next_best[1]
suffix = next_best[2]
new_options = generate_options(prefix_proba, prefix, suffix, lang_model, missed_model, optimism, cache)
# add only the solution potentioally no worse than the best + freedom
for new_option in new_options:
if new_option[0] < best_logprob + freedom:
heappush(heap, new_option)
if verbose:
print('heap size is', len(heap), 'after', i, 'iterations')
result = {}
for candidate in candidates:
if candidate[0] <= best_logprob + freedom:
result[candidate[1][1:-1]] = candidate[0]
return resultПрименим наш алгоритм для поиска возможных расшифровок аббревиатуры "brc".
result = noisy_channel('brc', lang_model, missed_model, verbose=True, freedom=1)
print(result)baseline score is 7.68318306228
(6.9148647560475442, ' ', 'brc ', '', 6.9148647560475442)
(6.755450684372974, ' b', 'rc ', '', 4.7044649199466617)
(5.8249119494605051, ' br', 'c ', '', 2.6863637325526679)
(7.088440394887126, ' brc', ' ', '', 1.7075575253192956)
(7.1392598304831516, ' bra', 'c ', 'a', 2.6863637325526679)
(7.6831830622750497, ' brc ', '', '', -0.0)
(8.0284469273601662, ' brac', ' ', '', 1.7075575253192956)
(8.3621576081202385, ' a', 'brc ', 'a', 6.776535093383159)
(7.6954572168460142, ' ab', 'rc ', '', 4.7044649199466617)
(6.7649184819335453, ' abr', 'c ', '', 2.6863637325526679)
(8.0284469273601662, ' abrc', ' ', '', 1.7075575253192956)
(8.0792663629561936, ' abra', 'c ', 'a', 2.6863637325526679)
(8.6231895947480908, ' abrc ', '', '', -0.0)
(8.6231895947480908, ' brac ', '', '', -0.0)
(8.6740629096242063, ' brca', ' ', 'a', 1.7075575253192956)
heap size is 0 after 15 iterations
{'brc': 7.6831830622750497, 'abrc': 8.6231895947480908, 'brac': 8.6231895947480908}Тестирование на хоббитах
По-настоящему протестировать написанные алгоритмы можно только с хорошей языковой моделью. Мне было интересно, как качественно модель сможет расшифровывать аббревиатуры, обучившись на заведомо ограниченном корпусе — одной книге, да ещё и специфической тематики. Первая книга, которая попалась мне под руку — это "The Lord Of The Rings: The Fellowship of the Ring". Что ж, посмотрим, как язык хоббитов может помочь расшифровать современные спортивные термины.
Для начала — код для обучения модели
import re
# считываем текст
with open('Fellowship_of_the_Ring.txt', encoding = 'utf-8') as f:
text = f.read()
# оставляем только буквы и пробелы в тексте
text2 = re.sub(r'[^a-z ]+', '', text.lower().replace('\n', ' '))
all_letters = ''.join(list(sorted(list(set(text2)))))
print(repr(all_letters)) # ' abcdefghijklmnopqrstuvwxyz'
# готовим обучающую выборку для модели опечаток:
missing_set = (
[(all_letters, '-' * len(all_letters))] * 3 # тут считаем все буквы пропущенными
+ [(all_letters, all_letters)] * 10 # тут считаем все буквы НЕ пропущенными
+ [('aeiouy', '------')] * 30 # тут считаем пропущенными только гласные
)
# обучаем обе модели
big_lang_m = LanguageNgramModel(order=4, smoothing=0.001, recursive=0.01)
big_lang_m.fit(text2)
big_err_m = MissingLetterModel(order=0, smoothing_missed=0.1)
big_err_m.fit(missing_set)' abcdefghijklmnopqrstuvwxyz'Четырёхграммную модель языка я выбрал, сравнив правдоподобие разных моделей на "тестовой выборке" — самом конце книги. Оказалось, что качество предсказания вероятности букв растёт с ростом порядка модели до 4. Ещё больший порядок я не стал использовать, ибо с ростом порядка сильно падает скорость работы модели.
for i in range(5):
tmp = LanguageNgramModel(i, 0.001, 0.01)
tmp.fit(text2[0:-5000])
print(i, tmp.single_log_proba(' ', text2[-5000:]))0 -13858.8600648
1 -11608.8867664
2 -9235.21749986
3 -7461.78935696
4 -6597.9544372Применим наш алгоритм к разным сокращениям. Загаданного мной Сэма, например, модель распознала без труда, да ещё и добавила других опций (впрочем, с более высоким скором, а значит, менее правдоподобных).
noisy_channel('sm', big_lang_m, big_err_m){'sam': 7.3438449620080997,
'same': 9.5091694602417469,
'some': 7.6890573935288824}Фродо тоже распознаётся без проблем
noisy_channel('frd', big_lang_m, big_err_m){'frodo': 6.8904938902680888}Кольцо угадывается однозначно.
noisy_channel('rng', big_lang_m, big_err_m)
{'ring': 7.6317120419343913}Прежде чем запускать "wtrbtl", проверим расшифровку по частям. С водой всё отлично.
noisy_channel('wtr', big_lang_m, big_err_m){'water': 8.6405279255413898}Бутылку модель распознаёт уже не так уверенно. Всё-таки битвы во "Властелине колец" упоминаются чаще бутылок.
noisy_channel('btl', big_lang_m, big_err_m){'battle': 12.620490427990008,
'bottle': 13.3327872548629,
'but all': 14.66815480120338,
'but ill': 15.387630853411283}Например, в таких вот словосочетаниях:
noisy_channel('batlhrse', big_lang_m, big_err_m){'battle horse': 25.194823785457018, 'battle horses': 27.40528952535044}Для бутылки с водой вылезло много альтернатив:
noisy_channel('wtrbtl', big_lang_m, big_err_m){'water battle': 23.76999162985074,
'water bottle': 23.962598992336815,
'water but all': 24.445047133561353,
'water but ill': 25.164523185769259,
'water but lay': 25.601336188357113,
'water but lie': 26.668305553728047}Зато баскетбол (никогда не виденный) модель распознала почти правильно, благо слово "basket" в обучающем тексте встречалось. Но чтобы это сделать, пришлось вручную увеличить ширину "луча", из которого модель выбирает варианты.
print(noisy_channel('bsktball', big_lang_m, big_err_m, freedom=5)){'bsktball': 33.193085889457429, 'basket ball': 33.985227947093364}Зато слово "ball" в обучающем тексте не встретилось ни разу, и самостоятельно модель его не восстановила (зато заподозрила в "bl" имя Бильбо). Слово "bowling" во "Властелине колец" тоже ни разу не встречалось, но исходя из какого-то общего представления о языке модель его всё-таки предложила.
print(noisy_channel('bwlingbl', big_lang_m, big_err_m, freedom=5)){'bwling blue': 31.318936077746862, 'bwling bilbo': 30.695249686758611, 'bwling ble': 34.490254059547475, 'bwling black': 31.980325659562851, 'bwling blow': 33.15061216480305, 'bewilling blue': 30.937989778499748, 'bewilling bilbo': 30.314303387511497, 'bewilling ble': 34.109307760300361, 'bewilling black': 31.599379360315737, 'bewilling blin': 34.685939493896406, 'bewilling blow': 32.769665865555929, 'bewilling bill': 32.156071732628014, 'bewilling below': 32.195518180732158, 'bwling bill': 32.537018031875135, 'bewilling belia': 32.550377929021479, 'bwling below': 32.576464479979279, 'bwling belia': 32.931324228268608, 'bwling belt': 33.203704016765826, 'bwling bling': 33.393527121566656, 'bwling bell': 34.180762531759534, 'bowling blue': 30.676613106535022, 'bowling bilbo': 30.052926715546771, 'bowling ble': 33.847931088335635, 'bowling black': 31.338002688351011, 'bowling blin': 34.42456282193168, 'bowling blow': 32.508289193591203, 'bowling bill': 31.894695060663285, 'bowling below': 31.934141508767446, 'bowling bl': 34.983414721126472, 'bowling blad': 34.992926061009179, 'bowling belia': 32.289001257056761, 'bwling blind': 35.000922570770712}Генерация упоротых текстов
Под конец, чтобы немного развеселить вас, я попробовал превратить в сокращения уже сам кусок текста "Властелина колец". Получилось странно.
part = text[10502:11149]
result = ''
for i, letter in enumerate(part):
if np.random.rand() * 0.5 < big_err_m.single_proba(part[0:i], letter):
result += letter
print(result)This bok s largly cncernd wth Hbbts, nd frm its pges readr ma dscver much f thir charctr nd littl f thir hstr. Furthr nfrmaton will als b fond n the selction from the Red Bok f Wstmarch that hs already ben publishd, ndr th ttle of The Hobbit. Tht stor was dervd from the arlir chpters of the Red Bok, cmpsed by Blbo hmslf, th first Hobbit t bcome famos n the world at large, nd clld b him There and Bck Again, sinc thy tld f his journey into th East and his return: n dvntr whch latr nvolved all the Hobbits n th grat vnts of that Ag that re hr rlatd.Языковую модель можно использовать, чтобы сгенерировать текст "в стиле Толкина", правда, без всякого смысла.
np.random.seed(20)
text = "Frodo"
for i in range(300):
proba = big_lang_m.predict_proba(text)
text += np.random.choice(proba.index, size=1, p=proba)[0]
print(text+'.')Frodo would me but them but his slipped in he see said pippin silent the names for follow as days are or the hobbits rever any forward spoke ened with and many when idle off they hand we cried plunged they lit a simply attack struggled itself it for in a what it was barrow the will the ears what all grow.Генерировать "с нуля" связные тексты наука о данных пока так и не научилась. Ибо для этого нужен самый настоящий искусственный интеллект, обладающий пониманием сюжета, разворачивавшегося когда-то в Средиземье.
Заключение
Обработка естественного языка — вообще-то очень сложная смесь науки, технологии, и магии. Даже учёные-лингвисты не до конца понимают законов, в соответствии с которыми устроена речь. И до тех времён, когда машины смогут в полном смысле слова понимать тексты, ещё очень не скоро.
Обработка естественного языка — это ещё и весело. Вооружившись парой статистических моделек, оказывается, можно и распознавать, и порождать неочевидные аббревиатуры. Для тех, кто хочет продолжить мои развлечения, вот полный код эксперимента.
А вот если заменить n-граммную модель на рекуррентную нейросетку, можно генерировать тексты более высокой степени связности (и даже почти компилируемый код). В ближайшем будущем я попробую сгенерить нейронкой типичную статью в стиле Хабра (который я уже распарсил), поэтому подписывайтесь и ждите :)