До:
После:
Заинтригованы? Но обо всем по порядку.
t-SNE — это очень популярный алгоритм, который позволяет снижать размерность ваших данных, чтобы их было проще визуализировать. Этот алгоритм может свернуть сотни измерений к всего двум, сохраняя при этом важные отношения между данными: чем ближе объекты располагаются в исходном пространстве, тем меньше расстояние между этими объектами в пространстве сокращенной размерности. t-SNE неплохо работает на маленьких и средних реальных наборах данных и не требует большого количества настроек гиперпараметров. Другими словами, если взять 100 000 точек и пропустить их через эту волшебный черный ящик, на выходе мы получим красивый график рассеяния.
Вот классический пример из области компьютерного зрения. Существует известный набор данных под названием MNIST, созданный Яном Лекуном (одним из создателей алгоритма обучения нейронных сетей методом обратного распространения ошибки — основы современного глубокого обучения) и другими. Его часто используют как универсальный набор данных для оценки идей, связанных с нейронными сетями, а также в научных исследованиях. MNIST — это 70 000 черно-белых изображений размера 28х28. Каждое из них — скан рукописной цифры из отрезка [0, 9]. Существует способ получения “бесконечного” набора MNIST, но не буду отклоняться от темы.
Таким образом, образец MNIST содержит
признака и может быть представлен в виде 784-мерного вектора. Векторы линейны, и в такой интерпретации мы теряем отношение расположения между отдельными пикселями, но все же в этом есть польза. Если попытаться представить, как выглядит наш набор данных в 784D, можно сойти с ума, если вы не специально обученный математик. Обычные люди могут потреблять информацию только размерности 3D, 2D или 1D. Неявно можно добавить еще одно измерение — время, но вряд ли кто-то скажет, что дисплей компьютера 3D только потому, что он обновляет картинку с частотой 100 Гц. Поэтому было бы здорово знать способ отобразить 784 измерения в два. Звучит невозможно? В общем случае так и есть. Вступает в игру принцип Дирихле: какое отображение мы не выберем, коллизий не избежать.
Иллюзия 3D -> 2D проекции в Shadowmatic
К счастью, можно выдвинуть следующие предположения:
Возникает вопрос: какая лучшая аппроксимирующая задача в пункте 2? К сожалению, “лучшей” нет. Качество снижения размерности субъективно и зависит от вашей конечной цели, как и при выборе метода кластеризации.
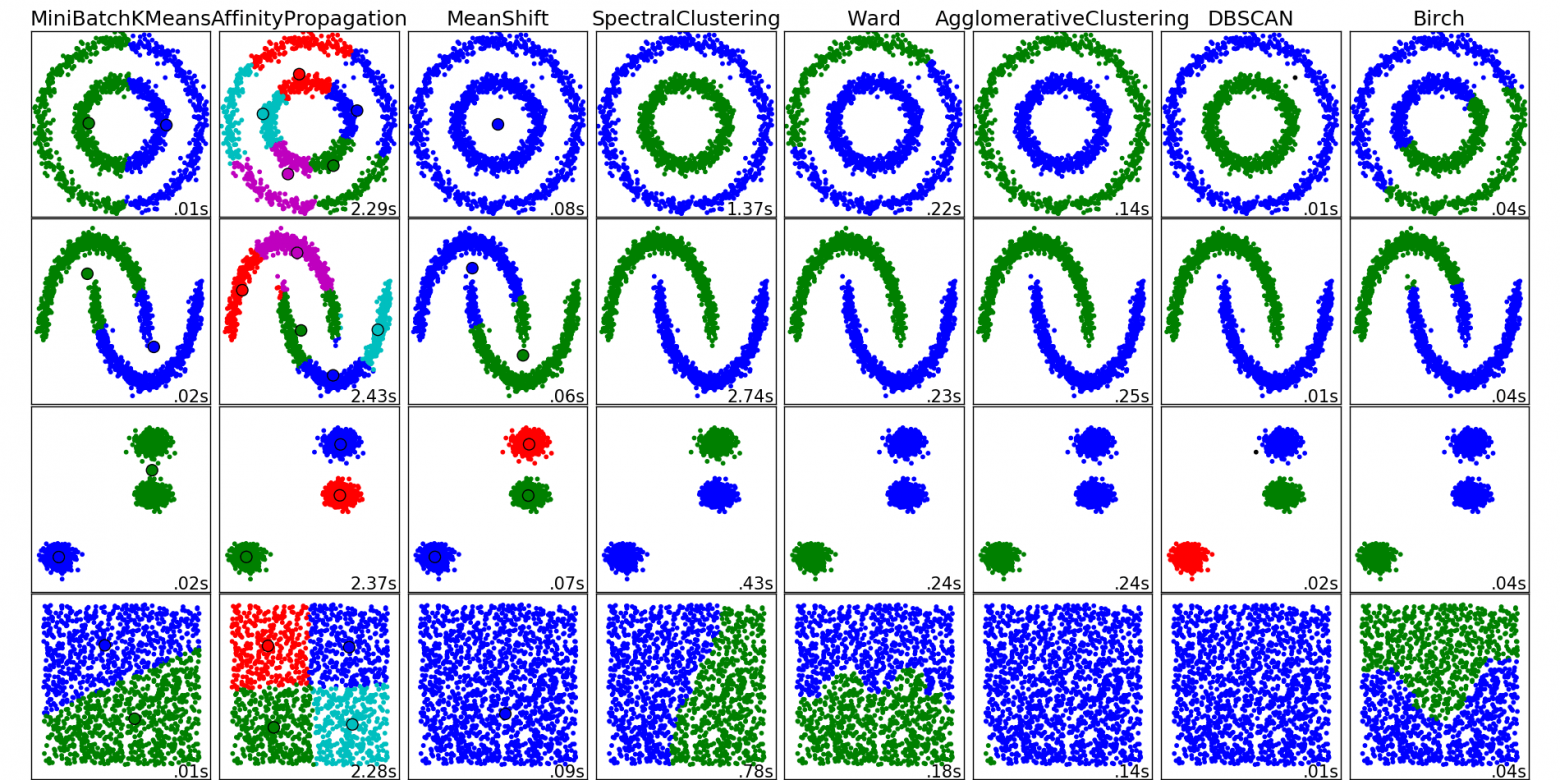
Разные алгоритмы кластеризации от sklearn
t-SNE — один из возможных алгоритмов сокращения размерности, которые называются алгоритмами укладки графа на плоскости (embedded algorithms). Ключевая идея — сохранять отношения “похожести”. Попробуйте сами.
Все это искусственные примеры, они хороши, но их недостаточно. Большинство реальных наборов данных напоминают облако с кональными кластерами. Например, MNIST выглядит так.
MNIST после применения t-SNE
Теперь давайте резко свернем в сторону и ознакомимся с понятием линейного программирования (linear programming, LP). Извините, но это не новый шаблон проектирования, Javascript фреймворк или стартап. Это математика:
Мы минимизируем скалярное произведение
и 
с учетов системы линейных неравенств, зависящих от , и требования, что все его координаты неотрицательны. LP — хорошо изученная тема в теории выпуклой оптимизации; как известно, эта задача решается за слабо полиномиальное время — обычно за 
, где n — количество переменных (размерность задачи). Но существуют и аппроксимирующие алгоритмы, выполняющиеся за линейное время. Эти алгоритмы используют умножение матриц и могут быть эффективно распараллеленны. Рай для программиста!
К LP могут быть сведены на удивление много задач. Возьмем, например, транспортную задачу.
Транспортная задача: пункты отправления (S) и пункты потребления (D)
Есть некоторое количество пунктов отправления и пунктов потребления, которые могут быть неравны. Каждый пункт потребления нуждается в определенном количестве товара. Каждый пункт отправления имеет ограниченные ресурсы и связан с некоторыми пунктами потребления. Основная задача состоит в следующем: каждое ребро
имеет свою стоимость 
, поэтому необходимо найти распределение поставок с минимальными затратами.
Строго говоря,
Последнее условие означает, что либо в пунктах отправления закончится товар, или спрос на товар иссякнет. Если
, выражение 8 можно нормализовать и упростить следующим образом:
Если заменить “отправление” и “потребление” на “землю”, то
приведет нас к задаче землекопа (Earth Mover’s Distance, EMD): минимизировать работу, необходимую для перетаскивания земли из одного набора куч в другие. Теперь вы знаете, что делать, если придется рыть ямы в земле.
Earth Mover’s Distance
Если же заменить “отправление” и “потребление” “гистограммами”, мы получим самый распространенный способ сравнения изображений эпохи “до глубокого обучения” (пример статьи). Этот метод лучше, чем наивный L2, так как он учитывает не только различия по абсолютной величине, но и разницу в расположении.
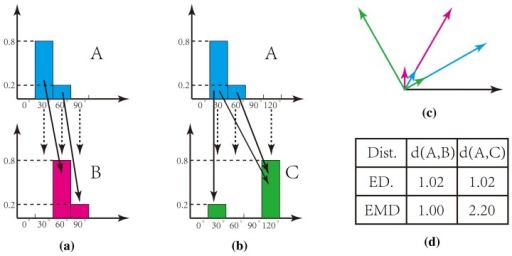
EMD лучше в сравнении гистограмм, чем Евклидово расстояние
Если заменить “отправление” и “потребление” словами, что мы придем к Word Mover’s Distance, эффективному способу сравнить значения двух предложений, используя word2vec для получения векторных представлений слов.
Word Mover’s Distance.
Если мы расслабим условия 5-8, выбросив 8, приняв
и превратив неравенства 6 и 7 в уравнения, добавив симметричные им неравенства, то получим задачу о назначениях (Linear Assignment Problem, LAP):
В отличие от транспортной задачи, можно доказать, что
— решение всегда двоично. Иными словами, или весь товар из пунктов отправления переходит в пункты потребления, или ничто никуда не переходит.
Как мы поняли из первого раздела, t-SNE, как и все алгоритмы укладки на плоскости, выдает на выходе диаграмму рассеяния. Хотя это идеально подходит для задач исследования наборов данных, иногда возникает потребность уложить исходную диаграмму на правильной сетке. Например, такая укладка необходима source{d}… скоро узнаем, зачем.
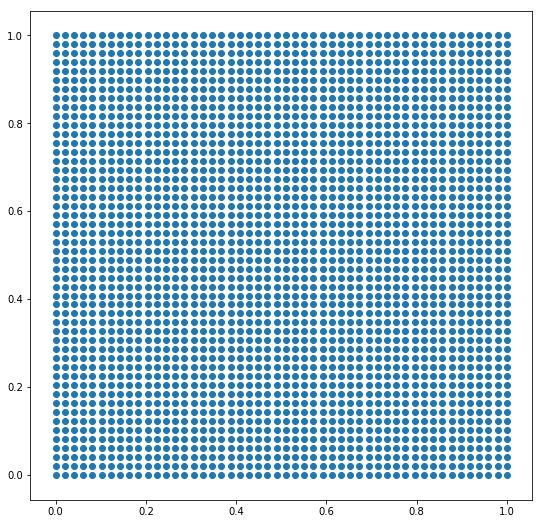
Правильная сетка
После применения t-SNE изобразим вместо точек цифры MNIST; вот как это выглядит:
Цифры MNIST после t-SNE
Не слишком понятно. Вот здесь возникает LAP: можно определить матрицу стоимости как парное евклидово расстояние между образцами t-SNE и узлами сетки, установим площадь сетки равной размеру набора данных
, и в результате решим проблему. Но как? Мы пока не рассказали ни об одном алгоритме.
Оказывается, существует огромное количество алгоритмов линейной оптимизации общего назначения, начиная с симплекс-метода и заканчивая крайне сложными инструментами. Алгоритмы, разработанные специально под определенную задачу, обычно сходятся значительно быстрее, хотя и обладают некоторыми ограничениями.
Венгерский алгоритм — один из специализированных методов, разработанный в 1950-х. Его сложность —. Он довольно просто для понимания и реализации, и поэтому популярен во многих проектах. Например, недавно он стал частью sсipy. К сожалению, он работает не быстро на больших объемах данных, а вариант scipy — особенно медленный. Я прождал час, чтобы обработать 2500 образцов MNIST, а Python все еще переваривал жертву.
Алгоритм Джонкера-Волгенанта (Jonker-Volgenant, JV) — улучшенный подход, разработанный в 1987. В его основе также прохождение кратчайшей аугментальной цепи, а его сложность также кубическая, но в нем с помощью некоторых хитрых приемов, разительно сокращается вычислительная нагрузка. Производительность многих алгоритмов укладки графов, включая JV, была подробно исследована в статье 2000 года Discrete Applied Mathematics. Заключение было следующим:
Тем не менее, у JV есть и недостаток. Он очень толерантен к различиям между парами элементов в матрице стоимостей. Например, если мы ищем кратчайший путь в графе с помощью алгоритма Дейкстры, и на этом графе появляются две очень близкие стоимости, алгоритм рискует уйти в бесконечный цикл. Если мы внимательно рассмотрим алгоритм Дейкстры, то обнаружим, что при достижении предела точности значений с плавающей точкой, могут произойти ужасные вещи. Обычный выход из ситуации — умножить матрицу стоимостей на некое большое число.
И все-таки самое заманчивое в JV для такого ленивого инженера, как я, — это пакет на Python 2, который представляет собой обертку древней реализации алгоритма на C: pyLAPJV. Этот код на C был написан Роем Джонкером в 1996 года для компании MagicLogic Optimization, президентом которой он является. Кроме того, что pyLAPJV больше не поддерживается, в ней есть незначительная проблема с выводом данных, которую я исправил в пулл-реквесте #2. Код на C надежен, но в нем не используется многопоточность или SIMD-инструкции. Мы, конечно, понимаем, что JV по своей природе однопоточен, и его не так просто распараллелить, тем не менее, мне удалось ускорить его почти вдвое, оптимизировав наиболее затратный этап — сокращеие аугментальной цепи — с помощью AVX2. В результате получился пакет src-d/lapjv на Python 3, доступный под лицензией MIT.
Сокращение аугментальной цепи в своей основе сводится к нахождению минимального и второго минимального элементов в массиве. Звучит просто, как и есть на самом деле, неоптимизированный код на C занимает 20 строк. Версия в AVX в 4 раза больше: мы посылаем минимальные значения на каждый процессорный элемент SIMD, выполняем blending, а затем применяем некоторые другие заклинания черной магии SIMD, которым я научился, пока работал над libSoundFeatureExtraction в Samsung.
Нахождение двух последовательных минимальных значений, C++
Нахождение двух последовательных минимальных значений, оптимизированный код с инструкциями AVX2
На моем ноутбуке lapjv укладывает 2500 образцов MNIST за 5 секунд, и вот он — драгоценный результат:
Решение задачи о назначениях для MNIST после t-SNE
Для подготовки этого поста я использовал Jupiter Notebook (исходник здесь).
Существует эффективный способ укладки образцов, обработанных t-SNE, на правильную сетку. Он основан на решении проблемы назначения (LAP) с помощью алгоритма Джонкера-Волгенанта, реализованного в src-d/lapjv. Этот алгоритм может быть масштабирован на 10 000 образцов.
После:
Заинтригованы? Но обо всем по порядку.
t-SNE
t-SNE — это очень популярный алгоритм, который позволяет снижать размерность ваших данных, чтобы их было проще визуализировать. Этот алгоритм может свернуть сотни измерений к всего двум, сохраняя при этом важные отношения между данными: чем ближе объекты располагаются в исходном пространстве, тем меньше расстояние между этими объектами в пространстве сокращенной размерности. t-SNE неплохо работает на маленьких и средних реальных наборах данных и не требует большого количества настроек гиперпараметров. Другими словами, если взять 100 000 точек и пропустить их через эту волшебный черный ящик, на выходе мы получим красивый график рассеяния.
Вот классический пример из области компьютерного зрения. Существует известный набор данных под названием MNIST, созданный Яном Лекуном (одним из создателей алгоритма обучения нейронных сетей методом обратного распространения ошибки — основы современного глубокого обучения) и другими. Его часто используют как универсальный набор данных для оценки идей, связанных с нейронными сетями, а также в научных исследованиях. MNIST — это 70 000 черно-белых изображений размера 28х28. Каждое из них — скан рукописной цифры из отрезка [0, 9]. Существует способ получения “бесконечного” набора MNIST, но не буду отклоняться от темы.
Таким образом, образец MNIST содержит
признака и может быть представлен в виде 784-мерного вектора. Векторы линейны, и в такой интерпретации мы теряем отношение расположения между отдельными пикселями, но все же в этом есть польза. Если попытаться представить, как выглядит наш набор данных в 784D, можно сойти с ума, если вы не специально обученный математик. Обычные люди могут потреблять информацию только размерности 3D, 2D или 1D. Неявно можно добавить еще одно измерение — время, но вряд ли кто-то скажет, что дисплей компьютера 3D только потому, что он обновляет картинку с частотой 100 Гц. Поэтому было бы здорово знать способ отобразить 784 измерения в два. Звучит невозможно? В общем случае так и есть. Вступает в игру принцип Дирихле: какое отображение мы не выберем, коллизий не избежать.
Иллюзия 3D -> 2D проекции в Shadowmatic
К счастью, можно выдвинуть следующие предположения:
- Исходное многомерное пространство разреженно, то есть вряд ли оно заполнено образцами однородно.
- Нам не нужно находить точное отображение, особенно зная, что его не существует. Вместо этого можно решить другую задачу, которая имеет гарантированное точное решение и аппроксимирует ожидаемый результат. Это напоминает принцип работы сжатия JPEG: результат никогда не бывает в точности идентичным, но изображение выглядит очень похожим на исходное.
Возникает вопрос: какая лучшая аппроксимирующая задача в пункте 2? К сожалению, “лучшей” нет. Качество снижения размерности субъективно и зависит от вашей конечной цели, как и при выборе метода кластеризации.
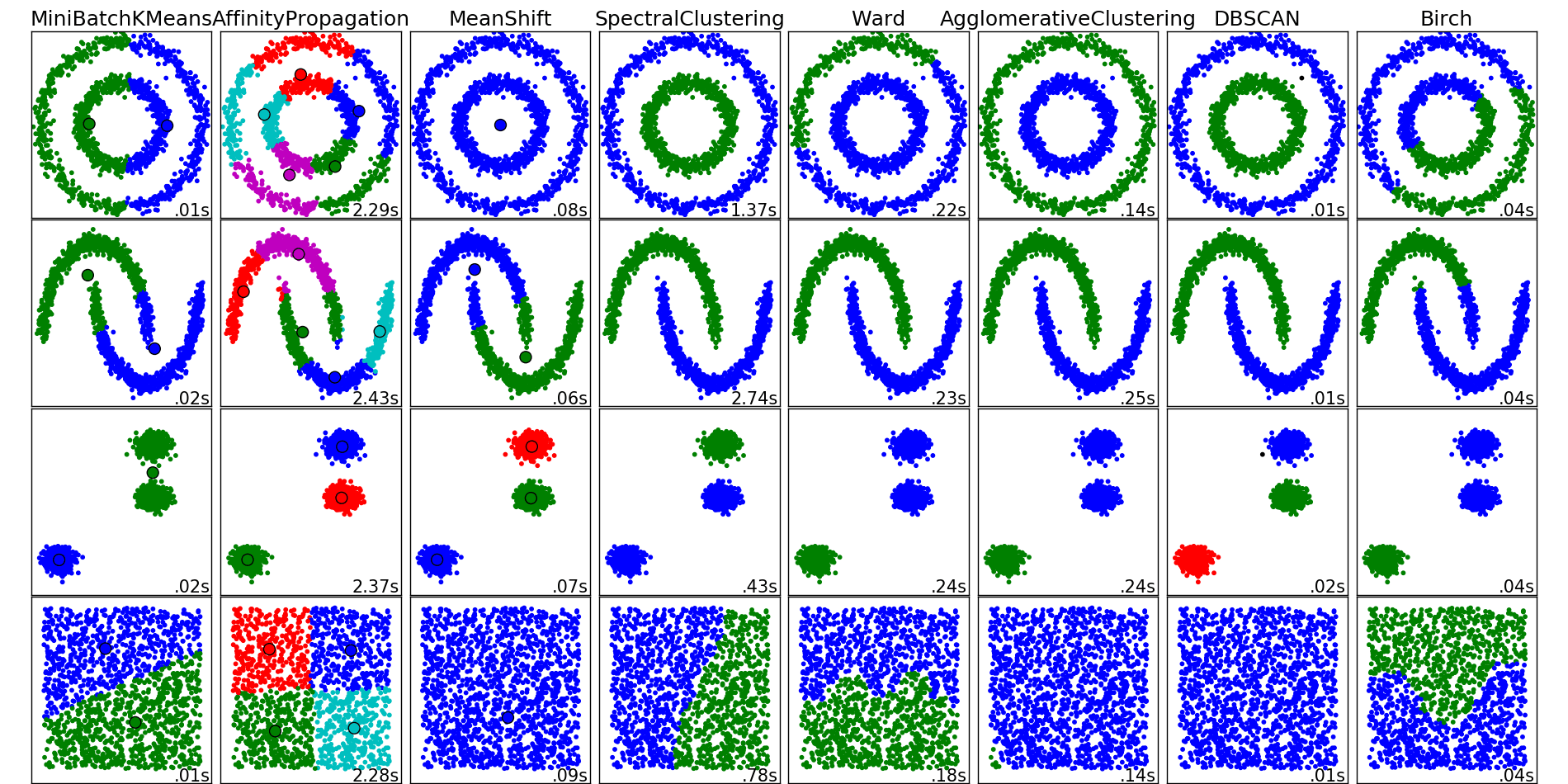
Разные алгоритмы кластеризации от sklearn
t-SNE — один из возможных алгоритмов сокращения размерности, которые называются алгоритмами укладки графа на плоскости (embedded algorithms). Ключевая идея — сохранять отношения “похожести”. Попробуйте сами.
Все это искусственные примеры, они хороши, но их недостаточно. Большинство реальных наборов данных напоминают облако с кональными кластерами. Например, MNIST выглядит так.
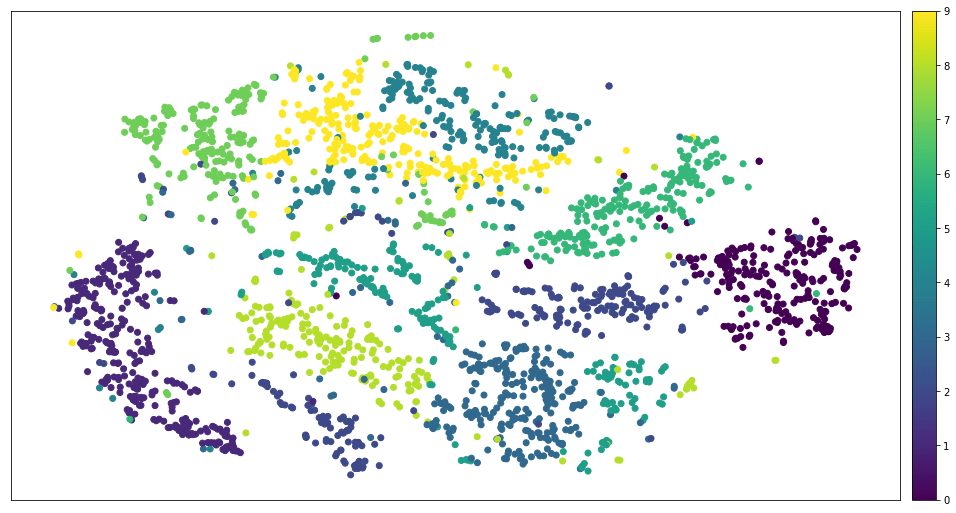
MNIST после применения t-SNE
Линейное программирование
Теперь давайте резко свернем в сторону и ознакомимся с понятием линейного программирования (linear programming, LP). Извините, но это не новый шаблон проектирования, Javascript фреймворк или стартап. Это математика:
Мы минимизируем скалярное произведение
и с учетов системы линейных неравенств, зависящих от , и требования, что все его координаты неотрицательны. LP — хорошо изученная тема в теории выпуклой оптимизации; как известно, эта задача решается за слабо полиномиальное время — обычно за , где n — количество переменных (размерность задачи). Но существуют и аппроксимирующие алгоритмы, выполняющиеся за линейное время. Эти алгоритмы используют умножение матриц и могут быть эффективно распараллеленны. Рай для программиста!К LP могут быть сведены на удивление много задач. Возьмем, например, транспортную задачу.
Транспортная задача: пункты отправления (S) и пункты потребления (D)
Есть некоторое количество пунктов отправления и пунктов потребления, которые могут быть неравны. Каждый пункт потребления нуждается в определенном количестве товара. Каждый пункт отправления имеет ограниченные ресурсы и связан с некоторыми пунктами потребления. Основная задача состоит в следующем: каждое ребро
имеет свою стоимость , поэтому необходимо найти распределение поставок с минимальными затратами.Строго говоря,
Последнее условие означает, что либо в пунктах отправления закончится товар, или спрос на товар иссякнет. Если
, выражение 8 можно нормализовать и упростить следующим образом:
Если заменить “отправление” и “потребление” на “землю”, то
приведет нас к задаче землекопа (Earth Mover’s Distance, EMD): минимизировать работу, необходимую для перетаскивания земли из одного набора куч в другие. Теперь вы знаете, что делать, если придется рыть ямы в земле.
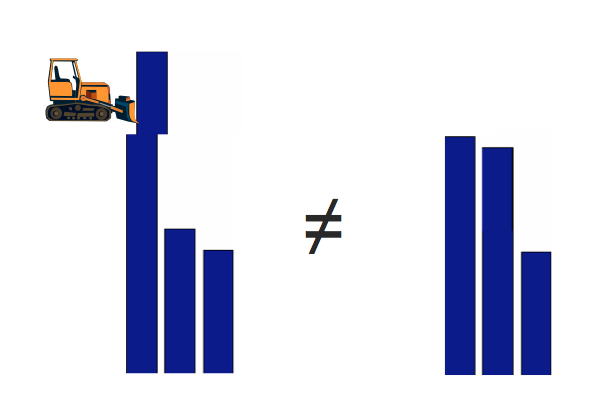
Earth Mover’s Distance
Если же заменить “отправление” и “потребление” “гистограммами”, мы получим самый распространенный способ сравнения изображений эпохи “до глубокого обучения” (пример статьи). Этот метод лучше, чем наивный L2, так как он учитывает не только различия по абсолютной величине, но и разницу в расположении.
EMD лучше в сравнении гистограмм, чем Евклидово расстояние
Если заменить “отправление” и “потребление” словами, что мы придем к Word Mover’s Distance, эффективному способу сравнить значения двух предложений, используя word2vec для получения векторных представлений слов.
Word Mover’s Distance.
Если мы расслабим условия 5-8, выбросив 8, приняв
и превратив неравенства 6 и 7 в уравнения, добавив симметричные им неравенства, то получим задачу о назначениях (Linear Assignment Problem, LAP):
В отличие от транспортной задачи, можно доказать, что
— решение всегда двоично. Иными словами, или весь товар из пунктов отправления переходит в пункты потребления, или ничто никуда не переходит.t-SNE LAP
Как мы поняли из первого раздела, t-SNE, как и все алгоритмы укладки на плоскости, выдает на выходе диаграмму рассеяния. Хотя это идеально подходит для задач исследования наборов данных, иногда возникает потребность уложить исходную диаграмму на правильной сетке. Например, такая укладка необходима source{d}… скоро узнаем, зачем.
Правильная сетка
После применения t-SNE изобразим вместо точек цифры MNIST; вот как это выглядит:
Цифры MNIST после t-SNE
Не слишком понятно. Вот здесь возникает LAP: можно определить матрицу стоимости как парное евклидово расстояние между образцами t-SNE и узлами сетки, установим площадь сетки равной размеру набора данных
, и в результате решим проблему. Но как? Мы пока не рассказали ни об одном алгоритме.Алгоритм Джонкера-Волгенанта
Оказывается, существует огромное количество алгоритмов линейной оптимизации общего назначения, начиная с симплекс-метода и заканчивая крайне сложными инструментами. Алгоритмы, разработанные специально под определенную задачу, обычно сходятся значительно быстрее, хотя и обладают некоторыми ограничениями.
Венгерский алгоритм — один из специализированных методов, разработанный в 1950-х. Его сложность —
. Он довольно просто для понимания и реализации, и поэтому популярен во многих проектах. Например, недавно он стал частью sсipy. К сожалению, он работает не быстро на больших объемах данных, а вариант scipy — особенно медленный. Я прождал час, чтобы обработать 2500 образцов MNIST, а Python все еще переваривал жертву.Алгоритм Джонкера-Волгенанта (Jonker-Volgenant, JV) — улучшенный подход, разработанный в 1987. В его основе также прохождение кратчайшей аугментальной цепи, а его сложность также кубическая, но в нем с помощью некоторых хитрых приемов, разительно сокращается вычислительная нагрузка. Производительность многих алгоритмов укладки графов, включая JV, была подробно исследована в статье 2000 года Discrete Applied Mathematics. Заключение было следующим:
“У JV хорошая и стабильная средняя производительность на всех классах (задач — прим. автора), и это лучший алгоритм как для случайных, так и для специфических задач”.
Тем не менее, у JV есть и недостаток. Он очень толерантен к различиям между парами элементов в матрице стоимостей. Например, если мы ищем кратчайший путь в графе с помощью алгоритма Дейкстры, и на этом графе появляются две очень близкие стоимости, алгоритм рискует уйти в бесконечный цикл. Если мы внимательно рассмотрим алгоритм Дейкстры, то обнаружим, что при достижении предела точности значений с плавающей точкой, могут произойти ужасные вещи. Обычный выход из ситуации — умножить матрицу стоимостей на некое большое число.
И все-таки самое заманчивое в JV для такого ленивого инженера, как я, — это пакет на Python 2, который представляет собой обертку древней реализации алгоритма на C: pyLAPJV. Этот код на C был написан Роем Джонкером в 1996 года для компании MagicLogic Optimization, президентом которой он является. Кроме того, что pyLAPJV больше не поддерживается, в ней есть незначительная проблема с выводом данных, которую я исправил в пулл-реквесте #2. Код на C надежен, но в нем не используется многопоточность или SIMD-инструкции. Мы, конечно, понимаем, что JV по своей природе однопоточен, и его не так просто распараллелить, тем не менее, мне удалось ускорить его почти вдвое, оптимизировав наиболее затратный этап — сокращеие аугментальной цепи — с помощью AVX2. В результате получился пакет src-d/lapjv на Python 3, доступный под лицензией MIT.
Сокращение аугментальной цепи в своей основе сводится к нахождению минимального и второго минимального элементов в массиве. Звучит просто, как и есть на самом деле, неоптимизированный код на C занимает 20 строк. Версия в AVX в 4 раза больше: мы посылаем минимальные значения на каждый процессорный элемент SIMD, выполняем blending, а затем применяем некоторые другие заклинания черной магии SIMD, которым я научился, пока работал над libSoundFeatureExtraction в Samsung.
template <typename idx, typename cost>
__attribute__((always_inline)) inline
std::tuple<cost, cost, idx, idx> find_umins(
idx dim, idx i, const cost *assigncost, const cost *v) {
cost umin = assigncost[i * dim] - v[0];
idx j1 = 0;
idx j2 = -1;
cost usubmin = std::numeric_limits<cost>::max();
for (idx j = 1; j < dim; j++) {
cost h = assigncost[i * dim + j] - v[j];
if (h < usubmin) {
if (h >= umin) {
usubmin = h;
j2 = j;
} else {
usubmin = umin;
umin = h;
j2 = j1;
j1 = j;
}
}
}
return std::make_tuple(umin, usubmin, j1, j2);
}Нахождение двух последовательных минимальных значений, C++
Показать код
template <typename idx>
__attribute__((always_inline)) inline
std::tuple<float, float, idx, idx> find_umins(
idx dim, idx i, const float *assigncost, const float *v) {
__m256i idxvec = _mm256_setr_epi32(0, 1, 2, 3, 4, 5, 6, 7);
__m256i j1vec = _mm256_set1_epi32(-1), j2vec = _mm256_set1_epi32(-1);
__m256 uminvec = _mm256_set1_ps(std::numeric_limits<float>::max()),
usubminvec = _mm256_set1_ps(std::numeric_limits<float>::max());
for (idx j = 0; j < dim - 7; j += 8) {
__m256 acvec = _mm256_loadu_ps(assigncost + i * dim + j);
__m256 vvec = _mm256_loadu_ps(v + j);
__m256 h = _mm256_sub_ps(acvec, vvec);
__m256 cmp = _mm256_cmp_ps(h, uminvec, _CMP_LE_OQ);
usubminvec = _mm256_blendv_ps(usubminvec, uminvec, cmp);
j2vec = _mm256_blendv_epi8(
j2vec, j1vec, reinterpret_cast<__m256i>(cmp));
uminvec = _mm256_blendv_ps(uminvec, h, cmp);
j1vec = _mm256_blendv_epi8(
j1vec, idxvec, reinterpret_cast<__m256i>(cmp));
cmp = _mm256_andnot_ps(cmp, _mm256_cmp_ps(h, usubminvec, _CMP_LT_OQ));
usubminvec = _mm256_blendv_ps(usubminvec, h, cmp);
j2vec = _mm256_blendv_epi8(
j2vec, idxvec, reinterpret_cast<__m256i>(cmp));
idxvec = _mm256_add_epi32(idxvec, _mm256_set1_epi32(8));
}
float uminmem[8], usubminmem[8];
int32_t j1mem[8], j2mem[8];
_mm256_storeu_ps(uminmem, uminvec);
_mm256_storeu_ps(usubminmem, usubminvec);
_mm256_storeu_si256(reinterpret_cast<__m256i*>(j1mem), j1vec);
_mm256_storeu_si256(reinterpret_cast<__m256i*>(j2mem), j2vec);
idx j1 = -1, j2 = -1;
float umin = std::numeric_limits<float>::max(),
usubmin = std::numeric_limits<float>::max();
for (int vi = 0; vi < 8; vi++) {
float h = uminmem[vi];
if (h < usubmin) {
idx jnew = j1mem[vi];
if (h >= umin) {
usubmin = h;
j2 = jnew;
} else {
usubmin = umin;
umin = h;
j2 = j1;
j1 = jnew;
}
}
}
for (int vi = 0; vi < 8; vi++) {
float h = usubminmem[vi];
if (h < usubmin) {
usubmin = h;
j2 = j2mem[vi];
}
}
for (idx j = dim & 0xFFFFFFF8u; j < dim; j++) {
float h = assigncost[i * dim + j] - v[j];
if (h < usubmin) {
if (h >= umin) {
usubmin = h;
j2 = j;
} else {
usubmin = umin;
umin = h;
j2 = j1;
j1 = j;
}
}
}
return std::make_tuple(umin, usubmin, j1, j2);
}Нахождение двух последовательных минимальных значений, оптимизированный код с инструкциями AVX2
На моем ноутбуке lapjv укладывает 2500 образцов MNIST за 5 секунд, и вот он — драгоценный результат:
Решение задачи о назначениях для MNIST после t-SNE
Notebook
Для подготовки этого поста я использовал Jupiter Notebook (исходник здесь).
Заключение
Существует эффективный способ укладки образцов, обработанных t-SNE, на правильную сетку. Он основан на решении проблемы назначения (LAP) с помощью алгоритма Джонкера-Волгенанта, реализованного в src-d/lapjv. Этот алгоритм может быть масштабирован на 10 000 образцов.
О, а приходите к нам работать? :)wunderfund.io — молодой фонд, который занимается высокочастотной алготорговлей. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Присоединяйтесь к нашей команде: wunderfund.io