Недавно kuznetsovin опубликовал пост об использовании Питона для анализа временных рядов в экономике. В качестве модели была выбрана «рабочая лошадка» эконометрики — ARIMA, пожалуй, одна из наиболее распространенных моделей для временных данных. В то же время, главный недостаток АRIMA-подобных моделей в том, что они не приспособлены для работы с нестационарными рядами. Например, если в данных присутствует тренд или сезонность, то математическое ожидание будет иметь разное значение в разных участках серии —  , что не есть хорошо. Для избежания этого, АRIMA предполагает работать не с исходными данными, а с их разностью (так называемое дифференцирование — от «taking a difference»). Все бы хорошо, но тут возникают две проблемы — (а) мы возможно теряем значимую информацию беря разницу ряда, и (б) упускается возможность разложить ряд данных на составляющие компоненты — тренд, цикл, и т.п. Поэтому, в данной статье я хотел бы привести альтернативный метод анализа — State Space Modeling (SSM), в русском переводе — Модель Пространства Состояний.
, что не есть хорошо. Для избежания этого, АRIMA предполагает работать не с исходными данными, а с их разностью (так называемое дифференцирование — от «taking a difference»). Все бы хорошо, но тут возникают две проблемы — (а) мы возможно теряем значимую информацию беря разницу ряда, и (б) упускается возможность разложить ряд данных на составляющие компоненты — тренд, цикл, и т.п. Поэтому, в данной статье я хотел бы привести альтернативный метод анализа — State Space Modeling (SSM), в русском переводе — Модель Пространства Состояний.
Итак, приступим.
Эта часть является одной из самых важных частей процесса, ибо если сделать ошибку сейчас, то вся остальная работа может быть просто потерей времени. Открываем данные по отгрузке товара на одном из складских комплексов Подмосковья, которые использовались в предыдущей статье. Построим график:
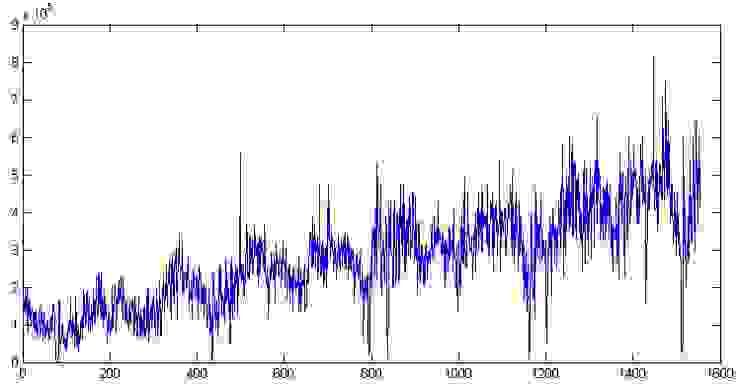
Во-первых, здесь явно присутствуют тренд и цикл с порядком около 300 дней. Теперь закроем график. Сходим покурим. Придем, откроем снова и посмотрим уже на сами цифры. Дата отгрузки указана в формате 01.09.2009, поэтому открываем в Экселе и если переведем данные в формат [$-F800]dddd, mmmm dd, yyyy], так чтобы показывался день недели, то заметим, что обычно в субботу значения по отгрузке намного меньше чем в остальные дни недели. Для примера две недели приведены на Графике 1. В общем, грузчик дядя Вася в субботу уходит домой пораньше смотреть футбол, а нам из-за этого придется дополнительно учитывать присутствие микроцикла с сезонностью в 7 дней. Кстати, мы не будем переводить данные в недельный интервал как в предыдущей статье, а продолжим работать с дневными данными.
Здесь я попытаюсь привести минимум теории, детальнее почему и откуда берутся все формулы можно прочитать в книге или я отвечу в комментариях.
Допустим, имеется некий временной ряд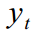 , в нашем случае — данные по отгрузке товара. Как правильно указал kuznetsovin в предыдущей статье, данные явно являются нестационарным рядом с порядком интегрирования равном 1, и процедура ARIMA требовала бы дифференцирования рядов. Но так как мы этого делать не хотим, то следуя Harvey [1993], допустим что данный ряд может быть представлен как модель с ненаблюдаемыми компонентами (Unobservable Сomponent model):
, в нашем случае — данные по отгрузке товара. Как правильно указал kuznetsovin в предыдущей статье, данные явно являются нестационарным рядом с порядком интегрирования равном 1, и процедура ARIMA требовала бы дифференцирования рядов. Но так как мы этого делать не хотим, то следуя Harvey [1993], допустим что данный ряд может быть представлен как модель с ненаблюдаемыми компонентами (Unobservable Сomponent model):

где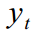 — наблюдаемый ряд в момент времени t, который состоит из ненаблюдаемых компонент: тренда
— наблюдаемый ряд в момент времени t, который состоит из ненаблюдаемых компонент: тренда 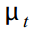 , цикла
, цикла  , сезонной переменной
, сезонной переменной  (в нашем случае равной одной неделе), и ошибки
(в нашем случае равной одной неделе), и ошибки  , которая нормально распределена как белый шум
, которая нормально распределена как белый шум  .
.
Тренд можно разнообразить, построив его в виде модели локального линейного тренда:
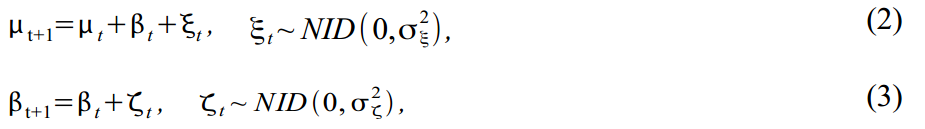
где (2) — собственно тренд и (3) — наклон тренда, каждый со своими ошибками. Такая модель дает множество вариантов моделирования тренда, от random walk with drift до integrated random walk model. Многие эконометристы часто убирают ошибку в (2) чтобы получитьчоткий гладкий тренд, а все случайные ошибки присвоить наклону тренда.
Стохастический цикл моделируется в виде суммы тригонометрических функций и их производных:

где обозначает частоту цикла, которая измеряется в радианах
обозначает частоту цикла, которая измеряется в радианах 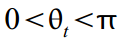 с периодом цикла соответственно
с периодом цикла соответственно 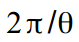 . Если есть настроение и лишнее время, можно допустить что частота изменяется со временем:
. Если есть настроение и лишнее время, можно допустить что частота изменяется со временем:  , но мы закроем глаза и допустим что цикл у нас вполне стационарен. Коэффициент затухания отвечает за то, чтобы наш цикл не вылетел за разумные пределы:
, но мы закроем глаза и допустим что цикл у нас вполне стационарен. Коэффициент затухания отвечает за то, чтобы наш цикл не вылетел за разумные пределы: 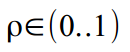 .
.
Ну и напоследок, недельный микроцикл с периодом s=7 также построим на основе суммы тригонометрических функций:

Теперь осталось все вышеприведенные формулы организовать в так называемый структурный формат подходящий для фильтра Калмана:
Уравнение измерения (measurement equation) описывает данные которые мы наблюдаем:

и уравнение перехода (transition equation) — описывает динамику переменных, которые составляют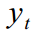 , но мы их не видим (так называемые unobserved или латентные переменные):
, но мы их не видим (так называемые unobserved или латентные переменные):

В нашем случае, имеется 10 латентных переменных которые были определены в уравнениях (2)-(6):

Теперь переведем все вышеприведенные формулы в матричный формат.
Матрица перехода в (7):

Неслабая такая матрица динамики латентных переменных в (8):

Вектор всех ошибок всех состояний (2)-(6):

оторый встраивается в уравнения динамики (8) с помощью матрицы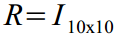 .
.
И, наконец, матрица вариаций всех ошибок и пертурбаций в (8):

Ок, теперь мы готовы курить Калман. Об алгоритме фильтра уже неоднократно писали, разве что у нас немного измененыимена и фамилии обозначения переменных. Поэтому особо останавливаться на теории не будем, кратенько только так, минут на сорок. Итак, есть видимая переменная 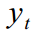 , и набор невидимых
, и набор невидимых 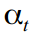 , для которых мы придумали динамику и структуру в (8)-(14), и которые мы и стараемся просчитать
, для которых мы придумали динамику и структуру в (8)-(14), и которые мы и стараемся просчитать в попугаях с помощью фильтра Калмана. Так как латентные состояния невидимы, модель может быть не особо верна, да и обязательно пристутствуют разные ошибки измерения, то саму 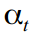 мы вряд ли встретим, а только ее математическое ожидание в момент времени t на основе наблюдаемых данных 1,..,t-1:
мы вряд ли встретим, а только ее математическое ожидание в момент времени t на основе наблюдаемых данных 1,..,t-1:  , которое обладает дисперсией
, которое обладает дисперсией  .
.
Предположим, что начальные значения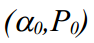 известны (в практической части реализации алгоритма мы просто зададим значения с потолка), фильтр Калмана состоит из набора итераций:
известны (в практической части реализации алгоритма мы просто зададим значения с потолка), фильтр Калмана состоит из набора итераций:

где – ошибка одноразового прогноза с вариацией
– ошибка одноразового прогноза с вариацией  ,
,  — калмановский коэффициент усиления (Kalman gain), ну и так далее. В общем, теория и в Африке одна и та же — что в физике, что в геолокации. Только обозначения переменных меняются по желанию автора.
— калмановский коэффициент усиления (Kalman gain), ну и так далее. В общем, теория и в Африке одна и та же — что в физике, что в геолокации. Только обозначения переменных меняются по желанию автора.
В дополнение к просчитыванию вектора состояний, нам еще интересно найти отдельные параметры модели, такие, например, как вариация ошибок, частота цикла, и параметр затухания цикла. Обзовем вектор искомых параметров как . Тогда если
. Тогда если  и
и  распределены по Гауссу, то логарифмическая функция правдоподобия (Log-likelihood function) параметров для наших данных будет:
распределены по Гауссу, то логарифмическая функция правдоподобия (Log-likelihood function) параметров для наших данных будет:
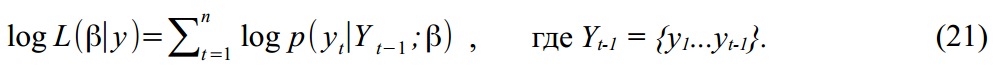
Так как и
и 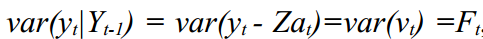 то результат из фильтра Калмана может быть использован чтобы вычислить функцию правдоподобия на основе ошибок фильтра:
то результат из фильтра Калмана может быть использован чтобы вычислить функцию правдоподобия на основе ошибок фильтра:
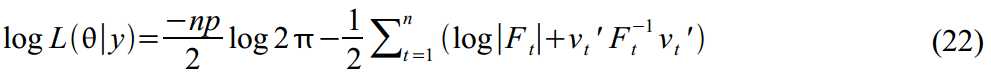
Максимизируя данную функцию, мы можем найти оценки требуемых параметров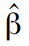 . На практике всегда проще минимизировать функции, поэтому в (22) мы добавили знаки минуса, и будем ее минимизировать.
. На практике всегда проще минимизировать функции, поэтому в (22) мы добавили знаки минуса, и будем ее минимизировать.
Теперь пару слов о еще одной wunderwaffe — Калмановском Сглаживании (Kalman smoother), [Durbin, J., and Koopman, 2003], которая вроде на Хабре еще не упоминалось. В общем, идея похожа, только фильтр Калмана просчитывает каждое следуещее значение в момент времени t на основе предыдущих данных 1..t-1:
в момент времени t на основе предыдущих данных 1..t-1:  . А Kalman Smoother немного читит, и, предполагая что у нас уже есть все данные, дает возможность уточнить
. А Kalman Smoother немного читит, и, предполагая что у нас уже есть все данные, дает возможность уточнить  смотря на весь временной ряд
смотря на весь временной ряд 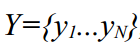 , то-есть, говоря простыми словами, он вычисляет
, то-есть, говоря простыми словами, он вычисляет 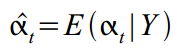 . Это хорошо работает когда у нас уже есть все наблюдения, и интересуют не будущие оценки, а более
. Это хорошо работает когда у нас уже есть все наблюдения, и интересуют не будущие оценки, а более лучше одеваться точные значения латентных переменных из которых складывается динамика ряда.
Сглаживание Калмана представляет собой обратную рекурсию:

где вектор сглаженных значений состояний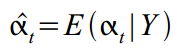 будет иметь наименьшую дисперсию
будет иметь наименьшую дисперсию  . Рекурсия сглаживания начинается в момент времени t=N, и запускается задом наперед задавая нулевые значения вектору
. Рекурсия сглаживания начинается в момент времени t=N, и запускается задом наперед задавая нулевые значения вектору 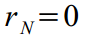 и его дисперсии
и его дисперсии  . Значения ошибки прогноза
. Значения ошибки прогноза  , ее дисперсия
, ее дисперсия  и Kalman gain
и Kalman gain  берутся из фильтра, который прогоняется в первый заход.
берутся из фильтра, который прогоняется в первый заход.
В общем, можно еще долго писать о теории, но уже руки чешутся потестировать. Итак, перейдем к эмпирическому материализму.
На оптимальность и скорость следующих программ в Матлабе я не претендую, я не настоящий сварщик, весь код писался для себя. Неэстетично, зато дешево, надежно и практично. Также код для фильтра и сглаживателя несколько избыточен, так как написан для разных вариантов инициализации и тп. Попытка выкинуть часть кода неизбежно приводила к вылетам Матлаба заплутавшего в матрицах и циклах, и поэтому я решил оставить все как есть.
Все работает все примерно так:
Собственно, код:
(p-values найденных оценок указаны в скобках)
Для удобства восприятия, показаны графики только для первых 600 дней, для всего ряда спрятаны под спойлеры.
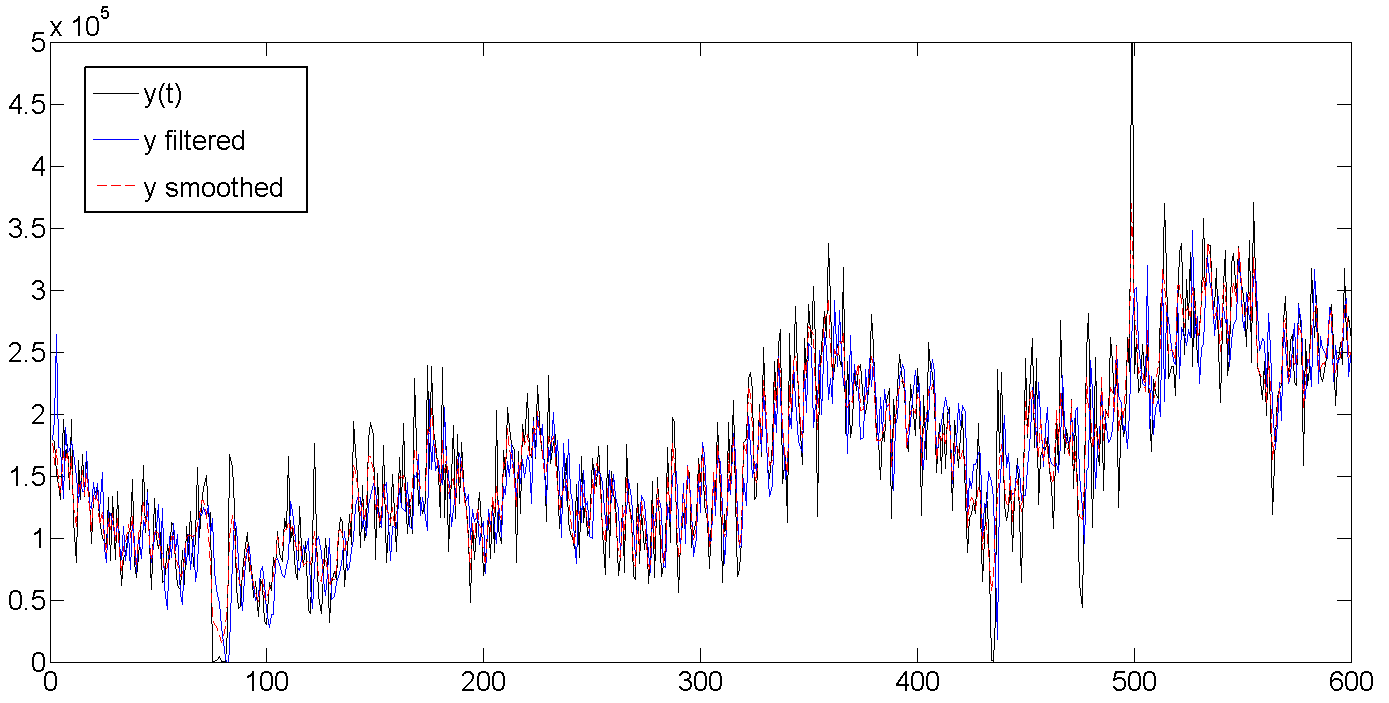
a. Исходные, отфильтрованные и сглаженные данные
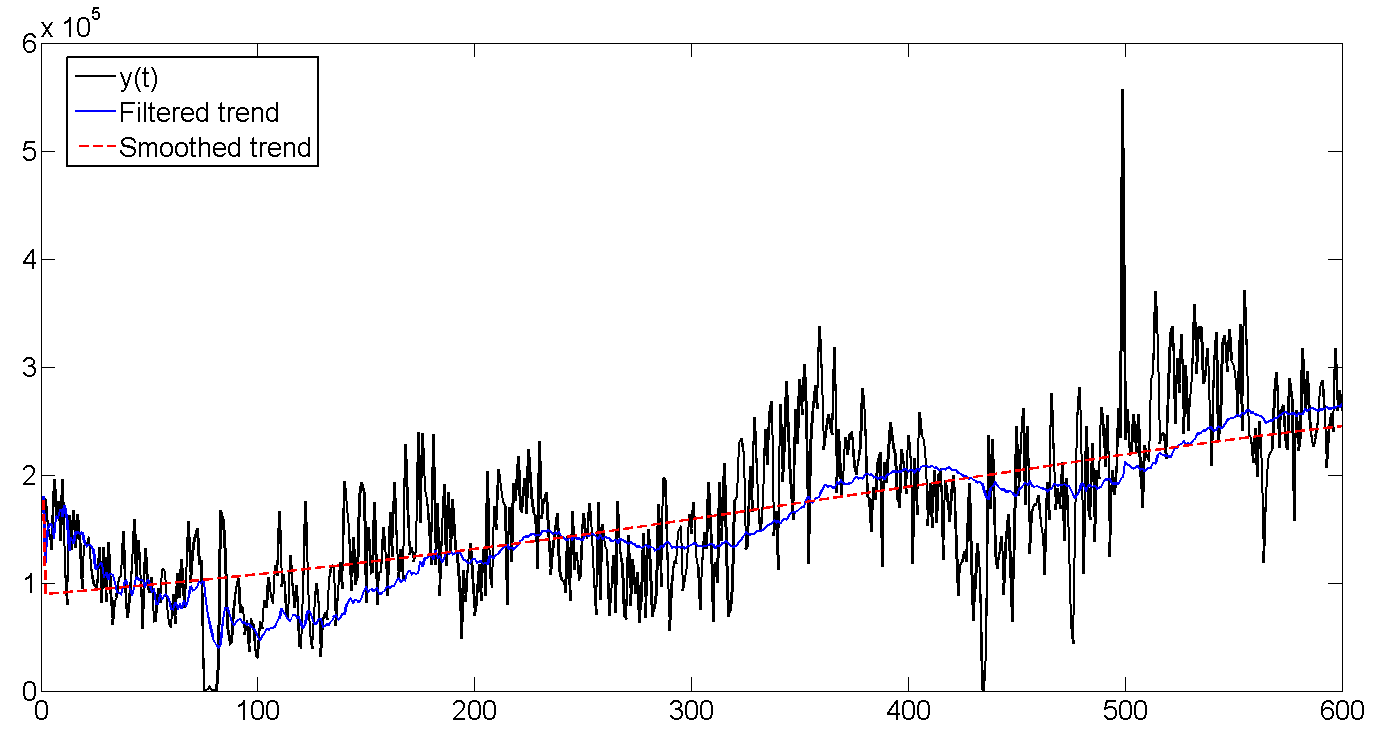
b. Исходные данные, отфильтрованный тренд, сглаженный тренд
Как видно, фильтр Калмана пытается угадать тренд на основе предыдущих значений, и поэтому колеблется вместе с линией партии, но немного запаздывая, пытаясь угадать куда дальше направятся наши данные. Сглаживатель Калмана же «видит» весь ряд, и поэтому тренд выглядит намного ровнее и спокойнее:
c. Отфильтрованный и сглаженный цикл
Как видно из таблицы с результатами, средняя длина цикла составляет порядка 362 дня, или практически один год (кто бы удивлялся). Также видно как в самом начале фильтр начинает калиброваться и совершенно не попадает в данные, ведь мы задали начальные значения латентных переменных равными нулю и очень большой дисперсией порядка 1e+10. Но обычно достаточно несколько (2-5) первых попыток чтобы фильтру попасть в ритм. Кстати, в этой работе использовалась точная инициализация фильтра (exact initialization), которая помогает отфильтрованным значениям быстрее сбежаться с данными.

d. Отфильтрованный и сглаженный недельный сезонный фактор
Постепенно растет количество отгрузок, увеличивается и дневная волатильность:

На основе полученных параметров и используя последние значения отфильтрованных состояних, строим прогноз на 70 дней (10 недель) и сравниваем с существующими данными. В целом прогноз выглядит неплохо, вот что фильтр животворящий делает. Особенно радует угаданная волатильность по дням недели. Если присмотреться ко всей длине построенного прогноза и включить воображение, то видно еще и как прогноз прогибается под годовой цикла отгрузки. Единственный момент где прогноз не сработал — с 26 по 32 день. Но там явно случилось почти недельное падение отгрузки, так же как и резкий скачок сразу за ней, которые вряд-ли возможно было предвидеть, так как подобный случай встречался только единожды в самом начале серий. В общем, а что упал, так то от помутненья.
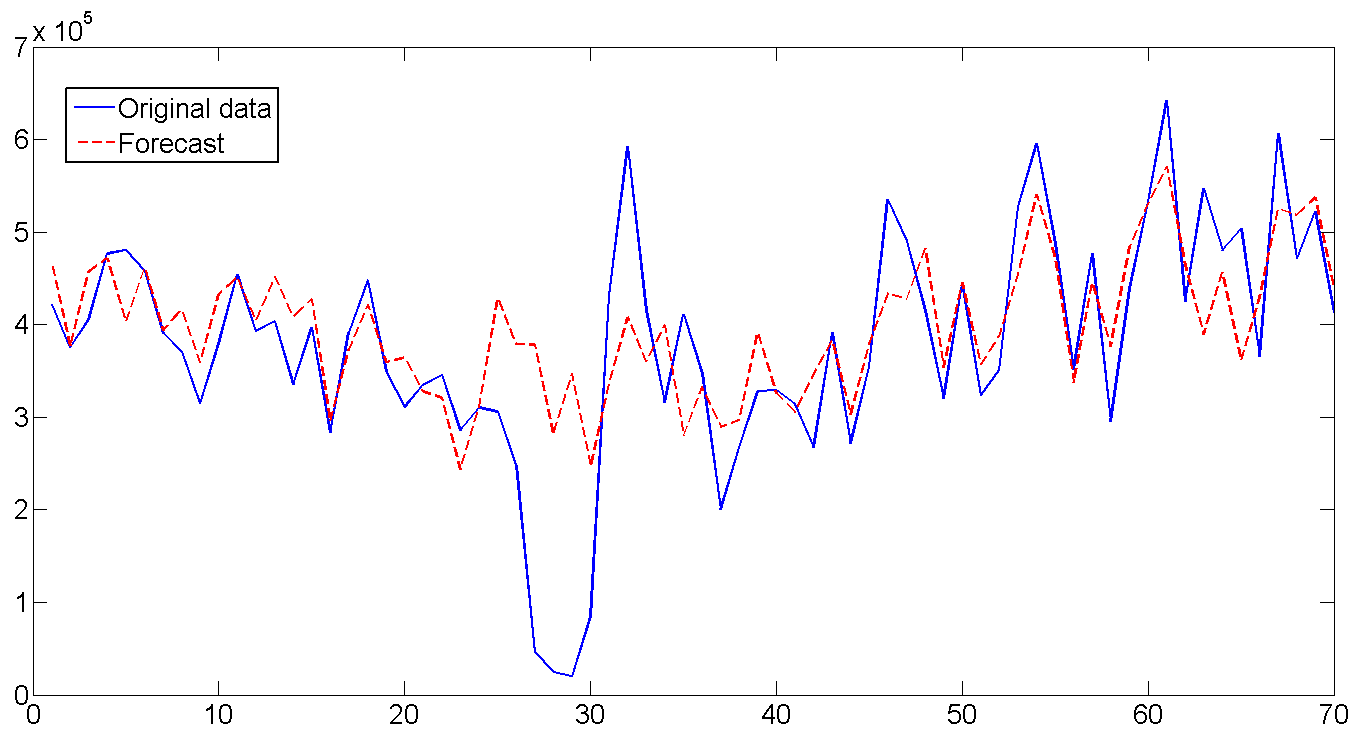
RMSE прогноза — 1.112e+005, на случай если мы захотим сравнить модель.
Ну вот и все.
Примечание
Для многих англоязычных названий в этой сфере перевод либо отсутствует, либо разнится у разных переводчиков, либо же коряв до полной невозможности использовать его в приличном обществе. Поэтому, многие имена и названия будут приведены в английском варианте. Для интересующихся — одна из лучших книг по моделированию SSM. Также оказалось, что в русскоязычном переводе хороших книг по теме практически нет. Как вариант — работа Александра Цыплакова, которая хоть и опубликована как отдельная статья, но является фактически копией книги в предельно сокращенном варианте.
Итак, приступим.
1. Начальный анализ данных
Эта часть является одной из самых важных частей процесса, ибо если сделать ошибку сейчас, то вся остальная работа может быть просто потерей времени. Открываем данные по отгрузке товара на одном из складских комплексов Подмосковья, которые использовались в предыдущей статье. Построим график:
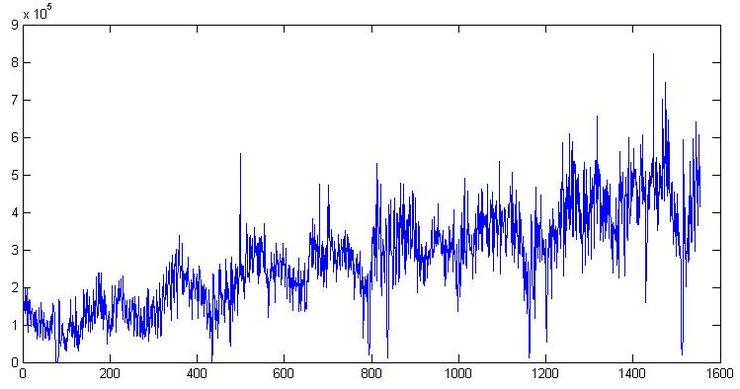
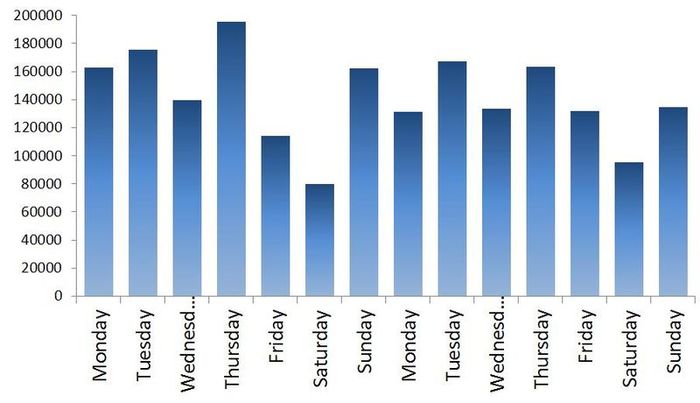
Во-первых, здесь явно присутствуют тренд и цикл с порядком около 300 дней. Теперь закроем график. Сходим покурим. Придем, откроем снова и посмотрим уже на сами цифры. Дата отгрузки указана в формате 01.09.2009, поэтому открываем в Экселе и если переведем данные в формат [$-F800]dddd, mmmm dd, yyyy], так чтобы показывался день недели, то заметим, что обычно в субботу значения по отгрузке намного меньше чем в остальные дни недели. Для примера две недели приведены на Графике 1. В общем, грузчик дядя Вася в субботу уходит домой пораньше смотреть футбол, а нам из-за этого придется дополнительно учитывать присутствие микроцикла с сезонностью в 7 дней. Кстати, мы не будем переводить данные в недельный интервал как в предыдущей статье, а продолжим работать с дневными данными.
График 1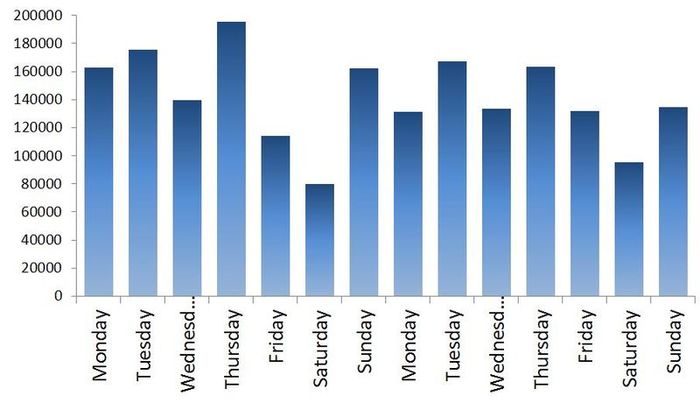
2. State Space Modes
Здесь я попытаюсь привести минимум теории, детальнее почему и откуда берутся все формулы можно прочитать в книге или я отвечу в комментариях.
Допустим, имеется некий временной ряд

где
Тренд можно разнообразить, построив его в виде модели локального линейного тренда:
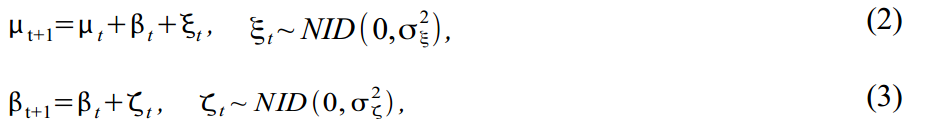
где (2) — собственно тренд и (3) — наклон тренда, каждый со своими ошибками. Такая модель дает множество вариантов моделирования тренда, от random walk with drift до integrated random walk model. Многие эконометристы часто убирают ошибку в (2) чтобы получить
Стохастический цикл моделируется в виде суммы тригонометрических функций и их производных:
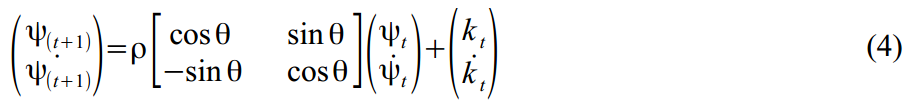
где
Ну и напоследок, недельный микроцикл с периодом s=7 также построим на основе суммы тригонометрических функций:

Теперь осталось все вышеприведенные формулы организовать в так называемый структурный формат подходящий для фильтра Калмана:
Уравнение измерения (measurement equation) описывает данные которые мы наблюдаем:

и уравнение перехода (transition equation) — описывает динамику переменных, которые составляют

В нашем случае, имеется 10 латентных переменных которые были определены в уравнениях (2)-(6):
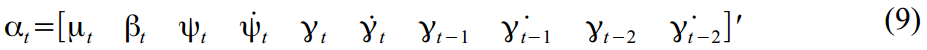
Теперь переведем все вышеприведенные формулы в матричный формат.
Матрица перехода в (7):
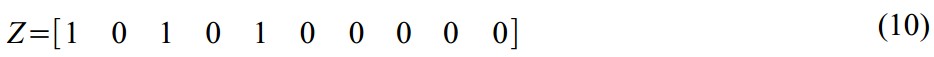
Неслабая такая матрица динамики латентных переменных в (8):
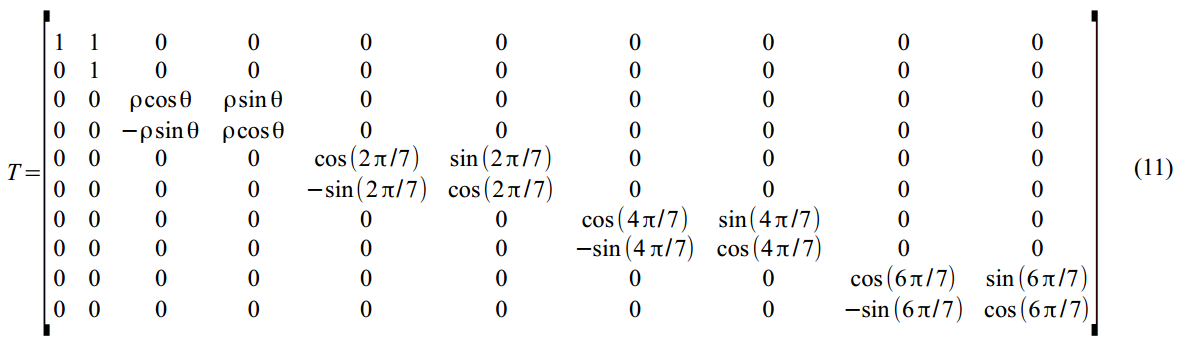
Вектор всех ошибок всех состояний (2)-(6):

оторый встраивается в уравнения динамики (8) с помощью матрицы
И, наконец, матрица вариаций всех ошибок и пертурбаций в (8):

3. Фильтр и Сглаживатель Калмана
Ок, теперь мы готовы курить Калман. Об алгоритме фильтра уже неоднократно писали, разве что у нас немного изменены
Предположим, что начальные значения

где
В дополнение к просчитыванию вектора состояний, нам еще интересно найти отдельные параметры модели, такие, например, как вариация ошибок, частота цикла, и параметр затухания цикла. Обзовем вектор искомых параметров как
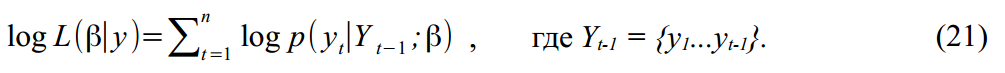
Так как
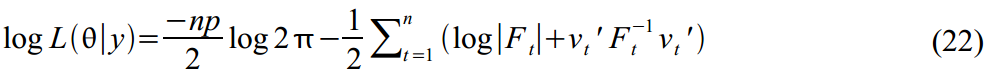
Максимизируя данную функцию, мы можем найти оценки требуемых параметров
Теперь пару слов о еще одной wunderwaffe — Калмановском Сглаживании (Kalman smoother), [Durbin, J., and Koopman, 2003], которая вроде на Хабре еще не упоминалось. В общем, идея похожа, только фильтр Калмана просчитывает каждое следуещее значение
Сглаживание Калмана представляет собой обратную рекурсию:

где вектор сглаженных значений состояний
В общем, можно еще долго писать о теории, но уже руки чешутся потестировать. Итак, перейдем к эмпирическому материализму.
4. Регрессия
На оптимальность и скорость следующих программ в Матлабе я не претендую, я не настоящий сварщик, весь код писался для себя. Неэстетично, зато дешево, надежно и практично. Также код для фильтра и сглаживателя несколько избыточен, так как написан для разных вариантов инициализации и тп. Попытка выкинуть часть кода неизбежно приводила к вылетам Матлаба заплутавшего в матрицах и циклах, и поэтому я решил оставить все как есть.
Все работает все примерно так:
- Главная программа otgr_ssm.m загружает данные, подготавливает структуру ssmopt, в которой записаны много ценных замечаний и важных переменных которые будут передаваться в разные места кода. Последние 70 значений по отгрузке (10 недель) отложим в сторону для сравнения с прогнозом, который обязательно построим в конце.
- Данные выгружаются в подпрограмму максимизации Log-likelihood function. Последняя процедура часто используется в эконометрике, поэтому была быстро на коленке написана в общем виде отдельной функцией mle_my.m чтобы не замусоривать основной код.
- так как искомые параметры включают дисперсии состояний, они должны быть строго положительны, что не всегда получается в ходе числовой оптимизации. Поэтому, сменим пешки на рюмашки и все входные значения дисперсий будут трансформированы как
 , а значение коэффициента затухания нормировано в диапазоне
, а значение коэффициента затухания нормировано в диапазоне 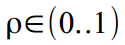 как
как  . Ну и на выходе, сооствественно трансформированы обратно, чтобы получить правильные значения —
. Ну и на выходе, сооствественно трансформированы обратно, чтобы получить правильные значения —  для вариаций и
для вариаций и  для коэффициента затухания. Значение ssmopt.trans указывает, надо ли трансформировать (1) или нет (0), и в какую сторону — 'in', или 'out'. Все это происходит с помощью отдельной функции transform.m
для коэффициента затухания. Значение ssmopt.trans указывает, надо ли трансформировать (1) или нет (0), и в какую сторону — 'in', или 'out'. Все это происходит с помощью отдельной функции transform.m - mle_my.m вызывает обьектную функцию f_obj.m, которая прогоняет фильтр Калмана (15)-(22) с помощью kfmy2.m, вычисляет значение Log-likelihood function (22), и, чтобы два раза не вставать, просчитывает Сглаживатель Калмана (23)-(27) используя ksmy2.m. Это все отправляется назад в mle_my.m, которая проверяет, достигли мы максимума функции (22) или нет. Если да, то все на выход, в пункт 5. Если нет, то повторяем шаги 2-4.
Самый первый запуск фильтра начинается с предположения что . Тут можно поиграться, так как переменных много, и мы ведем поиск глобального максимума шестимерной функции, поэтому возможны многие локальные экстремумы. По-хорошему, можно было бы построить графики возможных значений лог-функции и посмотреть на возможные экстремумы.
. Тут можно поиграться, так как переменных много, и мы ведем поиск глобального максимума шестимерной функции, поэтому возможны многие локальные экстремумы. По-хорошему, можно было бы построить графики возможных значений лог-функции и посмотреть на возможные экстремумы. - Выводим результаты — найденные параметры и графики. Заодно посчитаем предсказание для 70 дней и сравним его с реальными данными используя frcst.m
Собственно, код:
otgr_ssm.m
clear all;
clc;
close all;
format long;
%------------------- 1. Load and prepare data ------------------------------
load otgruzka.mat;
% Structure ssmopt contains several important records used throughout the code
ssmopt.frcst=70; % forecast length
yend=y(end-ssmopt.frcst+1:end); % saved last observation for the forecast comparison
y=y(1:end-ssmopt.frcst);
ssmopt.N=length(y);
ssmopt.trans=1; % transform estimated parameters to preserve positiveness of variances
ssmopt.sv=[5e+8;500;5e+8;5e+8;0.05;0.9]; % starting values
ssmopt.mle='f_obj'; % name of the objective function for the maximization
ssmopt.sv=transform(ssmopt.sv,'in',ssmopt);
ssmopt.filter='kfmy2'; % name of the function computing Kalman Filter
ssmopt.smooth='ksmy2'; % name of the function computing Kalman Smoother
%------------------- 2. Estimate the model ------------------------------
result=mle_my(y,ssmopt); % call Maximum Likelihood maximization function
b=transform(result.b,'out',ssmopt); % transform parameters back
% recompute data based on the correct non-transformed parameters
ssmopt.trans=0;
ssmopt.sv=b;
[LH,KF_out,Ksm_out] = feval(ssmopt.mle,b,y, ssmopt);
% Recover filtered states series - trend, cycle, and seasonal
a_trend=KF_out.Afilt(1,:);
a_cycle=KF_out.Afilt(3,:);
a_seas=KF_out.Afilt(5,:)+KF_out.Afilt(7,:)+KF_out.Afilt(9,:);
y_filt=a_trend+a_cycle+a_seas; % build the estimated filtered series Y
% Recover smoothed states series - trend, cycle, and seasonal
a_trendsm=Ksm_out.Asm(1,:);
a_cyclesm=Ksm_out.Asm(3,:);
a_seassm=Ksm_out.Asm(5,:)+Ksm_out.Asm(7,:)+Ksm_out.Asm(9,:);
y_smooth=a_trendsm+a_cyclesm+a_seassm; % build the estimated smoothed series Y
result=mle_my(y,ssmopt); % find correct Hessian for non-transformed parameters
%------------------- 3. Compute estimation statistics ------------------------------
%Find standard errors, and p-values
se=sqrt(abs(diag(inv(result.hessian)/ssmopt.N))); % s.e.(b)
tstat=b./se; % t-statistics
pval=2*(1-tcdf(abs(tstat),ssmopt.N-length(ssmopt.sv))); % p-value
% Display output
fprintf('Estimated parameters and p-values:\n');
out=[b pval]
period=2*pi/b(end-1)
% Compute R-squared
resid=y-y_filt; % estimation errors
SSE=resid*resid'; % Sum of Squared Errors
SST=(y-mean(y))*(y-mean(y))'; % Sum of Squares Total
R2=1-SSE/SST % R-squared'
%------------------- 4. Make Forecast ------------------------------
af0=KF_out.Afilt(:,end-ssmopt.frcst);
[yf,af]=frcst(b,y,ssmopt, af0);
%------------------- 5. Plot results ------------------------------
%p=ssmopt.N;
p=600;
t=[1:1:p];
figure(1)
plot(t,y(1:p),'k',t,y_filt(1:p),'b',t,y_smooth(1:p),'r--')
title('Original, Filtered, and Smoothed data')
legend('y(t)','y filtered','y smoothed');
figure(2)
plot(t,y(1:p),'k',t,a_trend(1:p),'b',t,a_trendsm(1:p),'r--')
title('Original data, Filtered and Smoothed trend')
legend('y(t)','Filtered trend','Smoothed trend');
figure(3)
plot(t,a_cycle(1:p),'b',t,a_cyclesm(1:p),'r--')
title('Filtered and Smoothed cycle')
legend('Filtered cycle','Smoothed cycle');
figure(4) % Filtered + smoothed seasonal
plot(t,a_seas(1:p),'b',t,a_seassm(1:p),'r--')
title('Filtered and Smoothed weekly seasonal')
legend('Filtered seasonal','Smoothed seasonal');
t=[1:1:ssmopt.frcst];
figure(5)
plot(t,yend,'b',t,yf,'r--')
title('Original data and Forecast')
legend('Original data','Forecast');
RMSE=sqrt(sum((yend - yf).^2)/ssmopt.frcst) % Root Mean Squared Error
mle_my.m
function result_mle=mle_my(y,mleopt);
warning off;
%---------------- 1. Set-up minimization options ----------------
options=optimset('fminunc');
options=optimset('LargeScale', 'off' , ...
'HessUpdate', 'bfgs' , ...
'LineSearchType', 'quadcubic' , ...
'GradObj' , 'off' , ...
'Display','off' , ...
'MaxIter' , 1000 , ...
'TolX', 1e-12 , ...
'TolFun' , 1e-12, ...
'DerivativeCheck' , 'off' , ...
'Diagnostics' , 'off' , ...
'MaxFunEvals', 1000);
%---------------- 2. Run minimization ----------------
[b,fval,exitflag,output,grad,hessian]=fminunc(mleopt.mle,mleopt.sv,options,y,mleopt);
warning on;
result_mle.b=b;
result_mle.fval=fval;
result_mle.output=output;
result_mle.hessian=hessian;
f_obj.m
function [obj,KF_out,Ksm_out]=f_obj_tr(b,y,ssmopt);
%---------------- 1. Recover parameters ------------------------------------
b=transform(b,'out',ssmopt);
s2_irr=b(1);
s2_tr=b(2);
s2_cyc=b(3);
s2_seas=b(4);
freq=b(5);
rho=b(6);
%---------------- 2. Build the model ------------------------------------
ssmopt.ssmodel.states=10;
ssmopt.ssmodel.Z=[1 0 1 0 1 0 1 0 1 0];
T1 = [1 1 0 0; 0 1 0 0; 0 0 rho*cos(freq) rho*sin(freq); 0 0 -rho*sin(freq) rho*cos(freq)];
T2=[cos(2*pi/7) sin(2*pi/7) 0 0 0 0;...
-sin(2*pi/7) cos(2*pi/7) 0 0 0 0;...
0 0 cos(4*pi/7) sin(4*pi/7) 0 0;...
0 0 -sin(4*pi/7) cos(4*pi/7) 0 0;...
0 0 0 0 cos(6*pi/7) sin(6*pi/7);...
0 0 0 0 -sin(6*pi/7) cos(6*pi/7)];
ssmopt.ssmodel.T = [T1 zeros(rows(T1),cols(T2));zeros(rows(T2),cols(T1)) T2];
ssmopt.ssmodel.R=eye(10); ssmopt.ssmodel.R(1,1)=0;
H=s2_irr;
Q=zeros(10,10);
Q(2,2)=s2_tr; Q(3,3)=s2_cyc; Q(4,4)=s2_cyc;
Q(5,5)=s2_seas; Q(6,6)=s2_seas; Q(7,7)=s2_seas; Q(8,8)=s2_seas;
Q(9,9)=s2_seas; Q(10,10)=s2_seas;
%---------------- 3. Suggest starting conditions for the states ------------------------
a0=[y(1);0;0;0;0;0;0;0;0;0];
P0=eye(ssmopt.ssmodel.states)*1e+10;
%---------------- 4. Run Kalman filter ------------------------
KF_out = feval(ssmopt.filter,y, ssmopt, Q, H, a0, P0);
obj=KF_out.LH;
%---------------- 5. Run Kalman smoother ------------------------
if nargout>2
ssmopt.ssmodel.num_etas=3; % number of the state variances (required for Kalman smoother)
Ksm_out = feval(ssmopt.smooth,KF_out, ssmopt);
end
kfmy2.m
% Kalman filter
% y[t] = Z*alpha[t] + eps, eps ~ N(0,H).
% alpha[t] = T*alpha[t-1] + R*eta, eta ~ N(0,Q).
% v[t]=y[t]-E(y[t]) = y[t]-Z*a[t]
% F[t]=var(v[t])
function KF_out = kfmy_koop(y, ssmopt, Q, H, a, P);
N=ssmopt.N;
m=ssmopt.ssmodel.states;
%---------------- 1. Recover parameters and prepare matrices ----------------
T=ssmopt.ssmodel.T;
Z=ssmopt.ssmodel.Z;
R=ssmopt.ssmodel.R;
KF_out.Vmat=zeros(1,N); KF_out.Fmat=zeros(1,N);
KF_out.Afilt=zeros(m,N); KF_out.Pfilt=zeros(m,m,N);
KF_out.Kmat=zeros(m,N); KF_out.Lmat=zeros(m,m,N);
LHmat=zeros(1,N);
if ~isfield(ssmopt,'exactcheck');
ssmopt.exactcheck=1; % set exact filter initialization by default
end;
%---------------- 2. Set default starting values for a and P , if none provided ----------------
Pinf=eye(m);
if nargin < 6
if ssmopt.exactcheck==1
P=zeros(m,m);
else
P=eye(m)*1000000000;
end
end
if nargin < 5
a=[y(1); zeros(m-1,1)];
end
KF_out.Afilt(:,1)= a;
KF_out.Pfilt(:,:,1) = P;
d=0;
%---------------- 3. Exact Filtering ----------------
if ssmopt.exactcheck==1
evals=10; % number of time steps to evaluate until Pinf converges to zero
KF_out.exact.F1=zeros(1,evals);
KF_out.exact.F2=zeros(1,evals);
KF_out.exact.L1=zeros(m,m,evals);
KF_out.exact.Pinf=zeros(m,m,evals); KF_out.exact.Pinf(:,:,1)=Pinf;
for i=1:evals
if sum(sum(Pinf))<1e-20;
d=i-1; % time point after which Pinf-->0, and after which we may start regular Kalman filter
break;
else
if sum(Pinf*Z')>0 % Pinf is not singular
F1=inv(Z*Pinf*Z'); F2=-F1*(Z*P*Z'+H)*F1;
K=T*Pinf*Z'*F1; K1=T*(P*Z'*F1+Pinf*Z'*F2);
L=T-K*Z; L1=-K1*Z;
P=T*Pinf*L1' + T*P*L' + R*Q*R';
Pinf=T*Pinf*L';
else
F1=Z*P*Z'+H; F2=F1;
K=T*P*Z'/F1;
L=T-K*Z; L1=L;
P=T*P*L' + R*Q*R';
Pinf=T*Pinf*T';
end
v=y(i) - Z*a;
a=T*a+K*v;
%save filtered estimates
KF_out.Afilt(:,i+1)=a; KF_out.Pfilt(:,:,i+1)=P;
KF_out.Vmat(i)=v; KF_out.Fmat(i)=F1;
KF_out.Kmat(:,i)=K; KF_out.Lmat(:,:,i)=L;
LHmat(i) = -0.5*(log(2*pi*F1) + v^2/F1);
%save exact values for smoother
KF_out.exact.F1(i)=F1;
KF_out.exact.F2(i)=F2;
KF_out.exact.L1(:,:,i)=L1;
KF_out.exact.Pinf(:,:,i+1)=Pinf;
end
end
end
%---------------- 4. Regular Filtering ----------------
for i=d+1:N
v=y(i) - Z*a;
f=Z*P*Z' + H;
K=T*P*Z'/f;
L=T-K*Z;
a=T*a+K*v;
P=T*P*L'+R*Q*R';
if i<N
KF_out.Afilt(:,i+1)=a; KF_out.Pfilt(:,:,i+1)=P;
end
KF_out.Vmat(i)=v; KF_out.Fmat(i)=f;
KF_out.Kmat(:,i)=K; KF_out.Lmat(:,:,i)=L;
LHmat(i) = -0.5*(log(2*pi*f) + v^2/f);
end
%---------------- 5. Prepare output ----------------
KF_out.LH=-sum(LHmat);
KF_out.Q=Q;
KF_out.H=H;
KF_out.exact.d=d;
end
ksmy2.m
function [Ksm_out, Kdism_out] = ksmy2(KF_out, ssmopt);
[m,N]=size(KF_out.Afilt);
meta=ssmopt.ssmodel.num_etas;
%---------------- 1. Recover filtered matrices ----------------
Fmat=KF_out.Fmat;
Vmat=KF_out.Vmat;
Pfilt=KF_out.Pfilt;
Afilt=KF_out.Afilt;
Q=KF_out.Q;
H=KF_out.H;
%---------------- 2. Recover Model structure ----------------
Z=ssmopt.ssmodel.Z;
T=ssmopt.ssmodel.T;
R=ssmopt.ssmodel.R;
Asm=zeros(m,N);
Psm=zeros(m,m,N);
rmat=zeros(m,N);
Nmat=zeros(m,m,N);
Eps=zeros(1,N);
Eta=zeros(meta,N);
Kmat=KF_out.Kmat;
Lmat=KF_out.Lmat;
if ~isfield(KF_out,'exact');
KF_out.exact.d=0;
end
d=KF_out.exact.d;
if KF_out.exact.d>0
L1=KF_out.exact.L1;
F1=KF_out.exact.F1;
F2=KF_out.exact.F2;
Pinf=KF_out.exact.Pinf;
end
%---------------- 3. Regular Smoothing for t=N..d+1 observations ----------------
for i=N:-1:d+1
r=Z'/Fmat(i)*Vmat(i) + Lmat(:,:,i)'*rmat(:,i);
N=Z'/Fmat(i)*Z + Lmat(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i);
Asm(:,i)=Afilt(:,i) + Pfilt(:,:,i)*r;
Psm(:,:,i)=Pfilt(:,:,i)-Pfilt(:,:,i)*N*Pfilt(:,:,i);
if i>1
rmat(:,i-1)=r;
Nmat(:,:,i-1)=N;
end
if nargout>1
Eps(i)=H*(1/(Fmat(i))*Vmat(i)-Kmat(:,i)'*rmat(:,i));
Eta(:,i)=Q*R'*rmat(:,i);
end
end
%---------------- 4. Exact Smoothing for t=d..1 observations ----------------
if KF_out.exact.d>0
r1=zeros(m,1); N1=zeros(m,m); N2=zeros(m,m);
for i=d:-1:1
if sum(Pinf(:,:,i)*Z')>0 %cond(Pinf)<1e+12 % Pinf is not singular
r1=Z'*F1(i)*Vmat(i) + Lmat(:,:,i)'*r1 + L1(:,:,i)'*rmat(:,i);
N2=Z'*F2(i)*Z + Lmat(:,:,i)'*N2*Lmat(:,:,i) + Lmat(:,:,i)'*N1*L1(:,:,i) + L1(:,:,i)'*N1*Lmat(:,:,i) + L1(:,:,i)'*Nmat(:,:,i)*L1(:,:,i);
N1=Z'*F1(i)*Z + Lmat(:,:,i)'*N1*Lmat(:,:,i) + L1(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i);
r=Lmat(:,:,i)'*r1;
N=Lmat(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i);
if nargout>1
Eps(i)=-H*Kmat(:,i)'*rmat(:,i);
Eta(:,i)=Q*R'*rmat(:,i);
end
else % Pinf is singular
r1=T'*rmat(:,i);
N2=T'*N2*T;
N1=T'*N1*Lmat(:,:,i);
r=Z'/(Fmat(i))*Vmat(i) + Lmat(:,:,i)'*rmat(:,i);
N=Z'/(Fmat(i))*Z + Lmat(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i);
if nargout>1
Eps(i)=H*(1/Fmat(i)*Vmat(i) - Kmat(:,i)'*rmat(:,i));
Eta(:,i)=Q*R'*rmat(:,i);
end
end
if i>1
rmat(:,i-1)=r;
Nmat(:,:,i-1)=N;
end
Asm(:,i)=Afilt(:,i) + Pfilt(:,:,i)*r + Pinf(:,:,i)*r1;
Psm(:,:,i)=Pfilt(:,:,i)-Pfilt(:,:,i)*N*Pfilt(:,:,i) - (Pinf(:,:,i)*N1*Pfilt(:,:,i))' - Pinf(:,:,i)*N1*Pfilt(:,:,i) - Pinf(:,:,i)*N2*Pinf(:,:,i);
end
end
%---------------- 5. Prepare output ----------------
Ksm_out.Asm=Asm;
Ksm_out.Psm=Psm;
Ksm_out.Kmat=Kmat;
Ksm_out.Lmat=Lmat;
Ksm_out.Nmat=Nmat;
Ksm_out.rmat=rmat;
Kdism_out.Eps=Eps;
Kdism_out.Eta=Eta;
transform.m
function b=transform(b,howto,ssmopt);
k=length(b);
if strcmp(howto,'in') % in-transformation
if ssmopt.trans==0 % no transformation
b=b;
end;
if ssmopt.trans==1 % transformation to preserve the positiveness of variances
b(1:k-1,:)=log(b(1:k-1,:));
b(k)=log(1/b(k)-1);
end;
else % out-transformation
if ssmopt.trans==0 % no transformation
b=b;
end;
if ssmopt.trans==1
b(1:k-1,:)=exp(b(1:k-1,:));
b(k)=1/(1+exp(b(k)));
end;
end
5. Результаты
(p-values найденных оценок указаны в скобках)
| Дисперсия ошибки наблюдаемого ряда |
1.77E+009 (0.00) |
| Дисперсия ошибки тренда |
348.73 (0.00) |
| Дисперсия цикла |
6.07E+008 (0.00) |
| Дисперсия ошибки сезонной компоненты |
3.91E+006 (0.00) |
| Частота цикла |
3.91E+006 (0.00) |
| Период цикла (в днях) | 362.6 (0.00) |
| Коэффициент затухания цикла |
0.891 (0.00) |
| R-квадрат регрессии | 0.78 |
6. Графики
Для удобства восприятия, показаны графики только для первых 600 дней, для всего ряда спрятаны под спойлеры.
a. Исходные, отфильтрованные и сглаженные данные
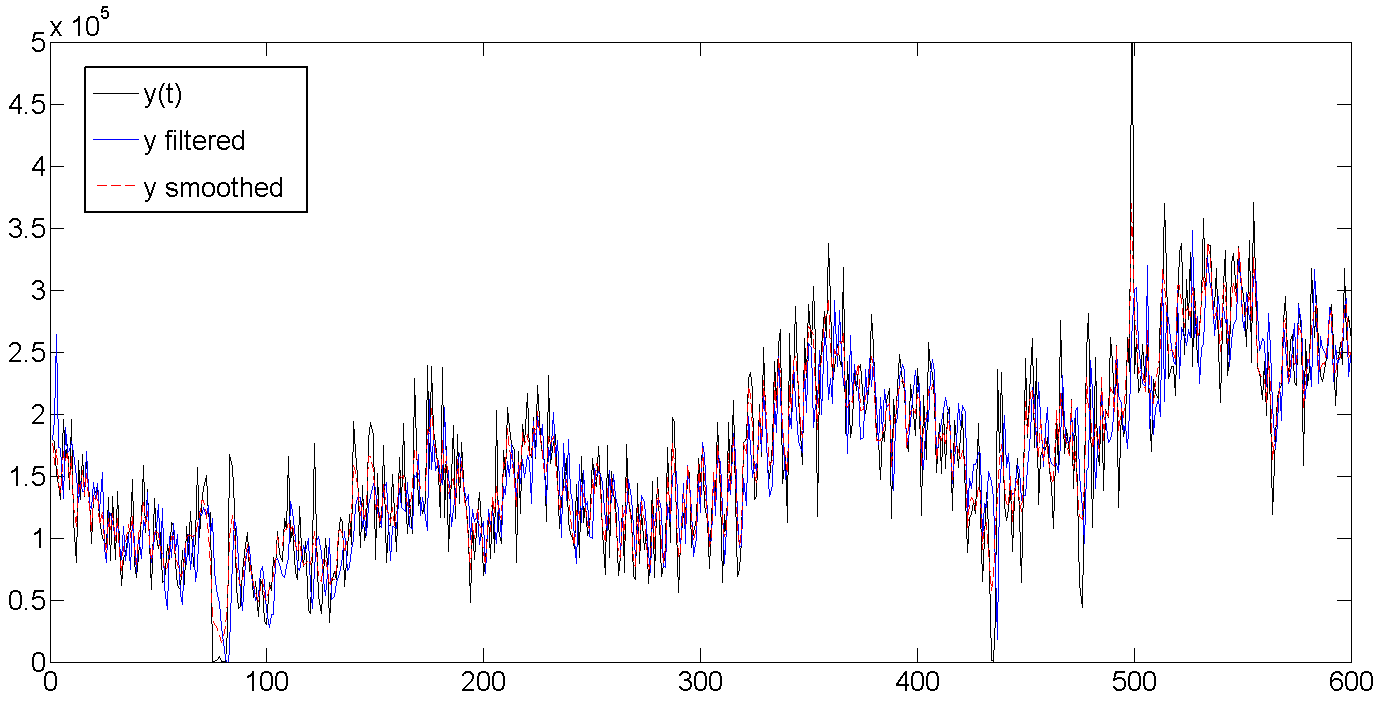
Весь ряд
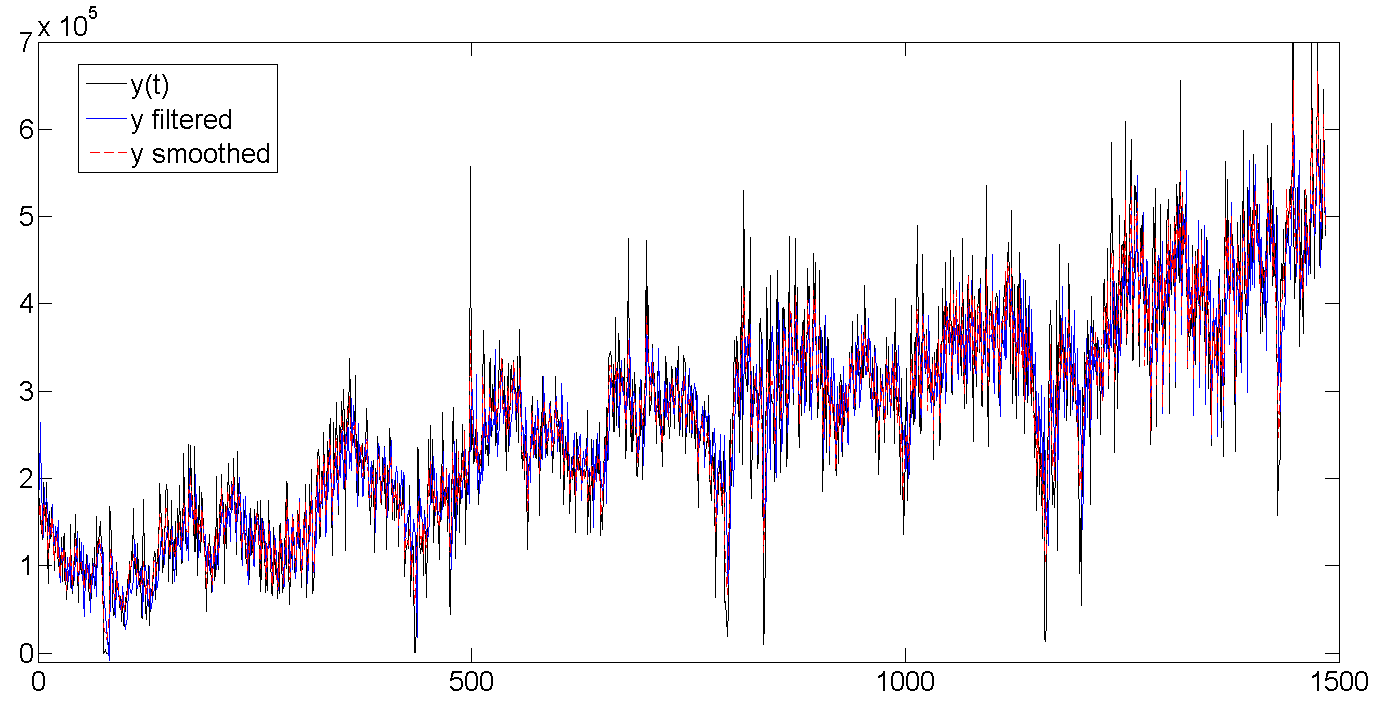
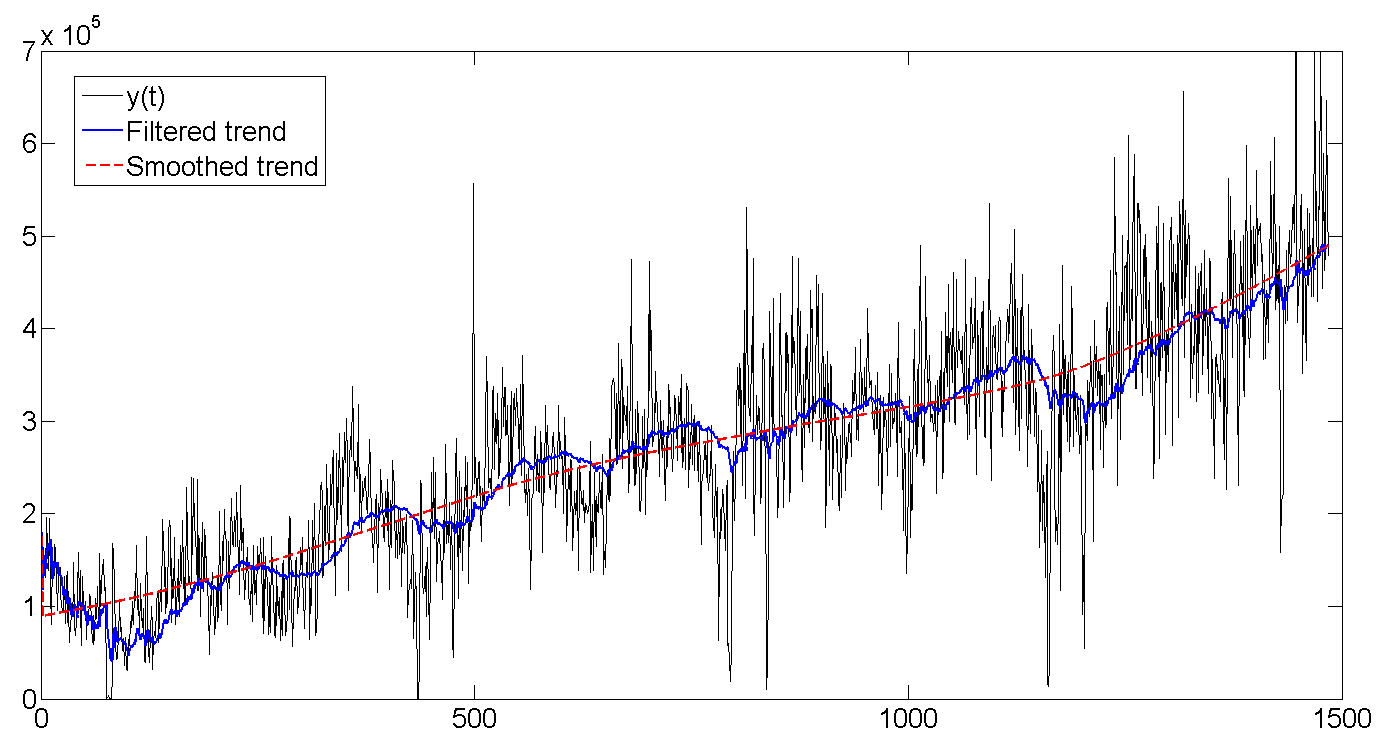
b. Исходные данные, отфильтрованный тренд, сглаженный тренд
Как видно, фильтр Калмана пытается угадать тренд на основе предыдущих значений, и поэтому колеблется вместе с линией партии, но немного запаздывая, пытаясь угадать куда дальше направятся наши данные. Сглаживатель Калмана же «видит» весь ряд, и поэтому тренд выглядит намного ровнее и спокойнее:

Весь ряд
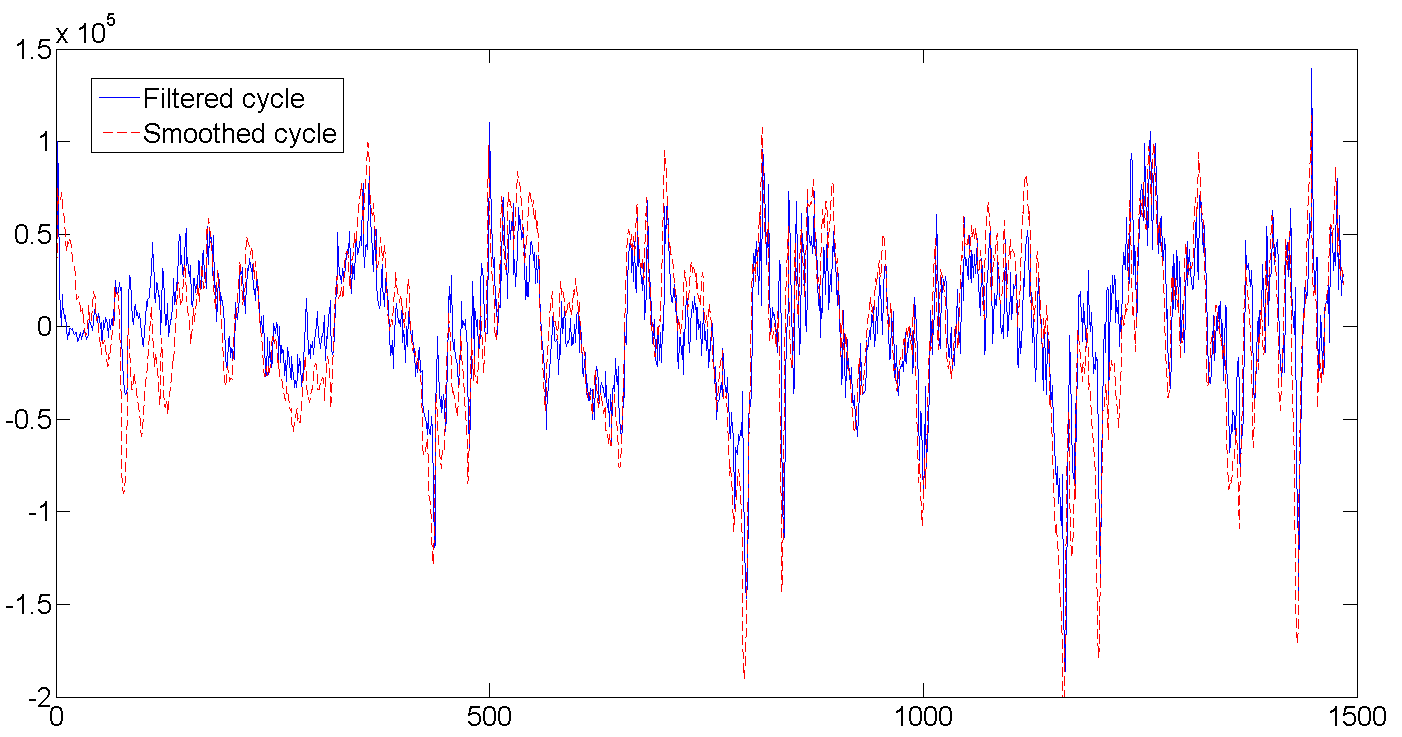
c. Отфильтрованный и сглаженный цикл
Как видно из таблицы с результатами, средняя длина цикла составляет порядка 362 дня, или практически один год (кто бы удивлялся). Также видно как в самом начале фильтр начинает калиброваться и совершенно не попадает в данные, ведь мы задали начальные значения латентных переменных равными нулю и очень большой дисперсией порядка 1e+10. Но обычно достаточно несколько (2-5) первых попыток чтобы фильтру попасть в ритм. Кстати, в этой работе использовалась точная инициализация фильтра (exact initialization), которая помогает отфильтрованным значениям быстрее сбежаться с данными.

Весь ряд
d. Отфильтрованный и сглаженный недельный сезонный фактор
Постепенно растет количество отгрузок, увеличивается и дневная волатильность:
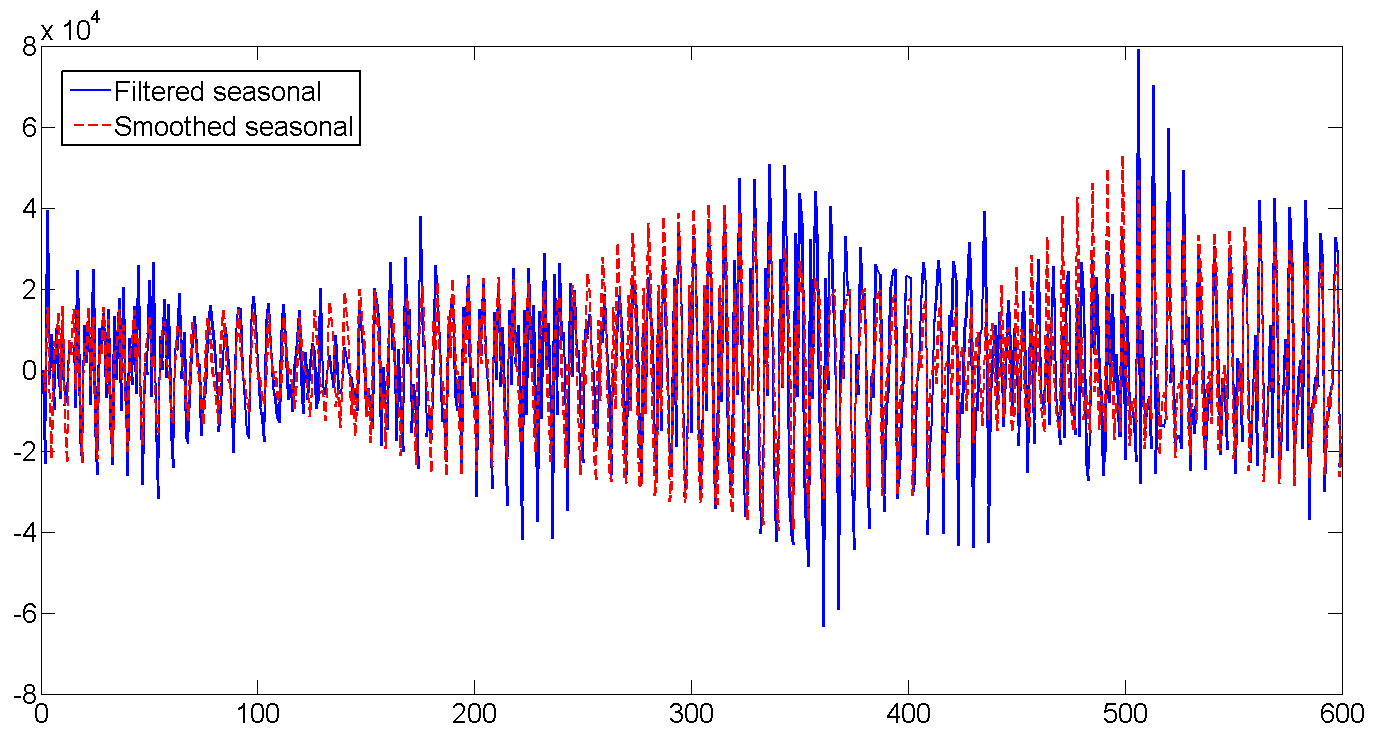
Весь ряд
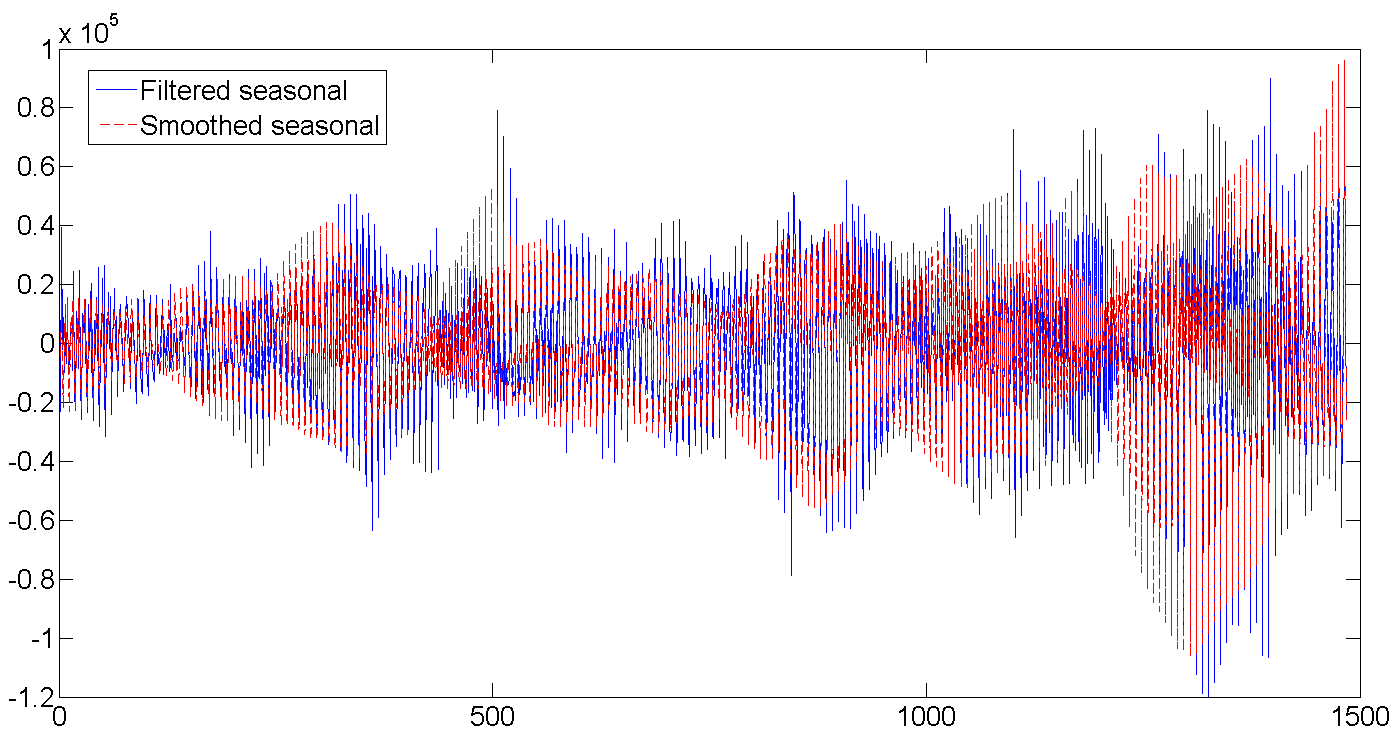
6. Прогноз
На основе полученных параметров и используя последние значения отфильтрованных состояних, строим прогноз на 70 дней (10 недель) и сравниваем с существующими данными. В целом прогноз выглядит неплохо, вот что фильтр животворящий делает. Особенно радует угаданная волатильность по дням недели. Если присмотреться ко всей длине построенного прогноза и включить воображение, то видно еще и как прогноз прогибается под годовой цикла отгрузки. Единственный момент где прогноз не сработал — с 26 по 32 день. Но там явно случилось почти недельное падение отгрузки, так же как и резкий скачок сразу за ней, которые вряд-ли возможно было предвидеть, так как подобный случай встречался только единожды в самом начале серий. В общем, а что упал, так то от помутненья.
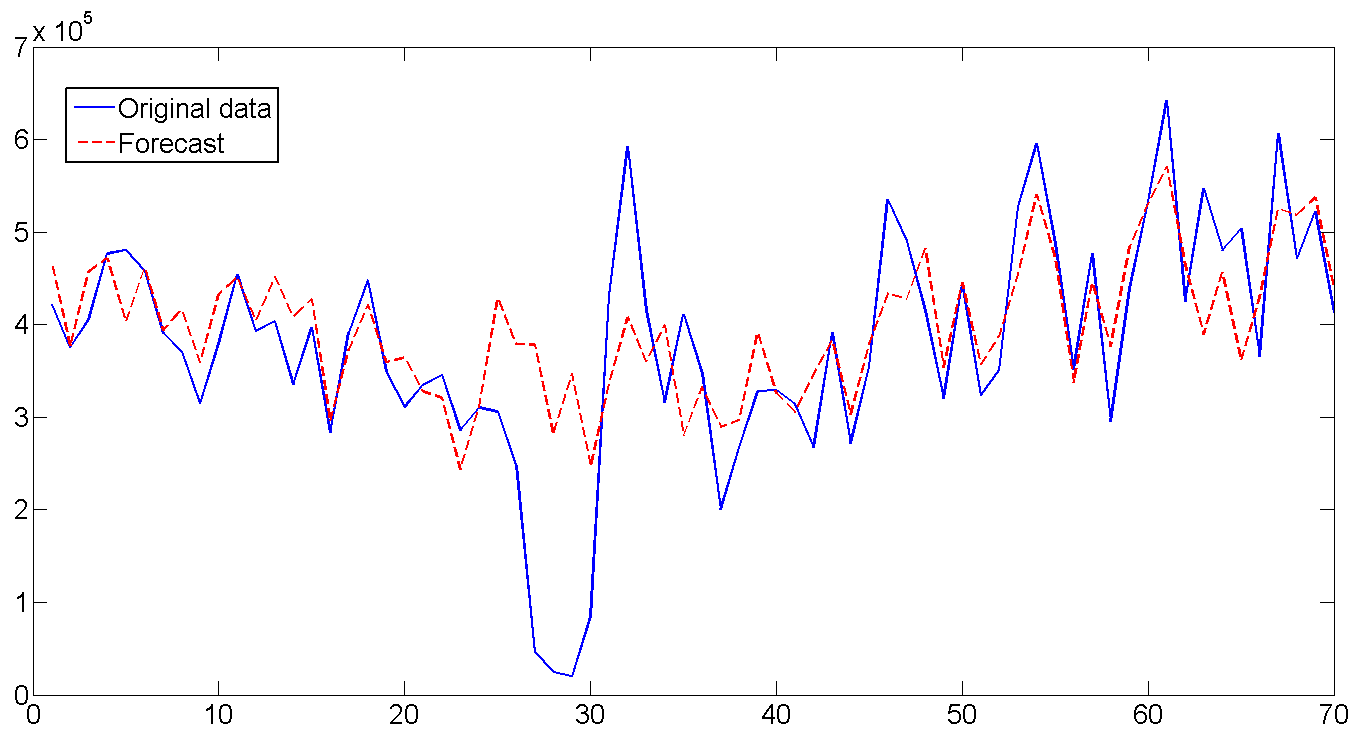
RMSE прогноза — 1.112e+005, на случай если мы захотим сравнить модель.
Ну вот и все.
Примечание
Не следует воспринимать State Space Models как что-то стоящее осторонь в эконометрике. Наоборот, они представляют собой обобщенный вариант для многих более специфических моделей. Например, MA(1) процесс

легко представить в форме SSM:
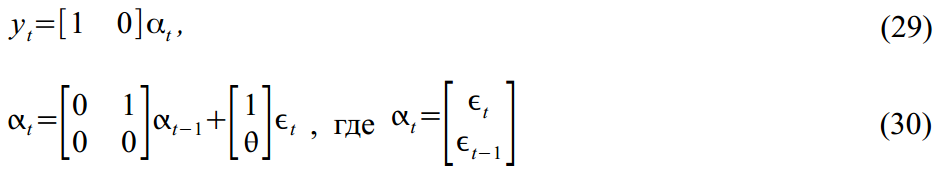
Или же ARMA(2,1) процесс:

Упакованный в формат SSM:


легко представить в форме SSM:
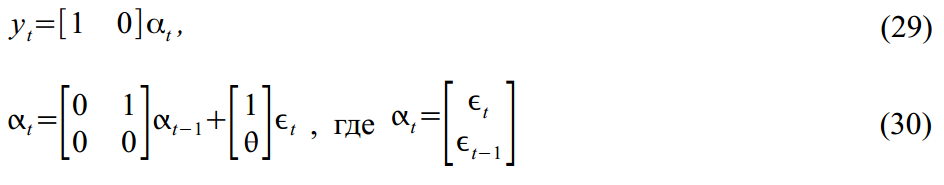
Или же ARMA(2,1) процесс:
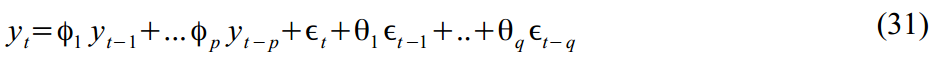
Упакованный в формат SSM:
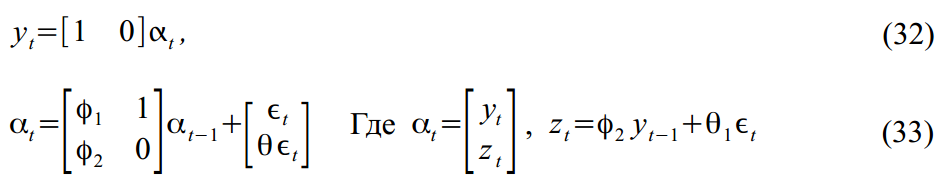
Литература по теме
- Durbin, J., and Koopman, S.J. «Time Series Analysis by State Space Methods». Oxford: Oxford University Press, 2001.
- Durbin, J., and Koopman, S.J. «A simple and efficient simulation smoother for state space time series analysis» Biometrika vol. 89, issue 3, 2002.
- Harvey, A.C., and Jaeger, A. “Detrending, stylised facts and the business cycle.” Journal of Applied Econometrics (8), 1993.
- Harvey, A.C. «Forecasting, Structural Time Series Models and the Kalman Filter». Cambridge: Cambridge University Press, 1989.