Сразу хочу извиниться, про робастные эстиматоры я узнал из англоязычной литературы, поэтому некоторые термины являются прямой калькой с английских, вполне может быть, что в русскоязычной литературе тема о робастных оценках имеет какие то свои устойчивые обороты.
Во время учебы в университете курс статистики, который нам читали (а это было больше, чем 15 лет назад), был самый что ни на есть типичный: введение через теорию вероятностей и часто встречающиеся распределения. Больше в голове с тех пор про этот семестровый курс ничего не осталось. Мне кажется, что в курсе статистической физики многое дается много лучше. Уже значительно позже жизнь столкнула меня с медицинской физикой, где статистические методы являются одним из основных инструментов анализа данных, полученных, например, с помощью ЯМР томографии. Тут то я первый раз и встретил термин robust statistics и robust estimators. Сразу оговорюсь, я покажу только простые примеры применения робастных эстиматоров и дам ссылки на литературу, интересующиеся легко смогут углубить и расширить свои знания использую список литературы в конце этой заметки. Давайте разберем самый простой пример наиболее часто встречающийся, чтобы продемонстрировать надежную оценку в какой либо выборке. Предположим, что студент Вася сидит на физическом практикуме и записывает показания некоего прибора:
4.5
4.1
5.2
5.5
3.9
4.3
5.7
6.0
45
47
Прибор работает не так чтобы очень точно плюс к этому Вася отвлекается на разговоры с соседкой по практикуму Леной. Как результат в последних двух записях Василий не ставит десятичную точку и, вуаля, – мы имеет проблему.
Шаг первый, мы упорядочиваем нашу выборку по возрастанию и вычисляем среднее значение
mean = 13.12
Сразу видно, что среднее значение далеко от реального среднего благодаря двум последним выбросам (outliers), попавшим в выборку. Самый простой способ оценить среднее неучитывая влияние выбросов – это медиана
median = 5.35
Таким образом, самый простой робастный эстиматор – это медиана, действительно, мы можем видеть, что до 50% данных можно “загрязнить” разного рода выбросами, но оценка медианы не изменится. На этом простом примере можно ввести сразу несколько понятий: что такое робастность в статистике (устойчивость оценок по отношению к выбросам в данных), насколько используемый эстиматор является робастным (как сильно можно “загрязнить” данные без существенного изменения полученных оценок) [1]. Можно ли улучшить медианную оценку? Безусловно можно ввести еще более надежный эстиматор известный как абсолютное отклонение от медианы (median absolute deviation or MAD)
MAD = median(|xi-median[xj]|)
в случае нормального распределения вводят численный фактор перед MAD, позволяющий сохранить оценку без изменений. Как несложно заметить устойчивость MAD так же является 50%.
Огромное практическое применение робастные эстиматоры нашли в линейных регрессиях. В случае линейной зависимости (x,y) часто надо получить хорошо обусловленные оценки такой зависимости (часто в случае мультивариативной регрессии)
y = Bx +E ,
где B уже может представлять собой матрицу коэффициентов, Е некий шум, портящий наши измерения, и x набор параметров (вектор), который мы собственно и хотим оценить, используя измерянные значения y (вектор). Самый простой и всем известный способ это сделать – это метод наименьших квадратов (МНК) [2]. В принципе, очень легко убедиться, что МНК робастным эстиматором не является и его робастная надежность равна 0%, т.к. даже один выброс может существенно изменить оценку. Один из самых математических красивых трюков, позволяющий улучшить оценку, называется least trimmed squares или метод “урезанных” квадратов (МУК). Его идея заключается в тривиальной модификации оригинального МНК, в которой урезают число используемых оценок, т.е.:
оригинальный МНК
МУК
где r_i это уже упорядоченные ошибки оценок (y – O(x)), т.е. r_1<r_2<...<r_N. Опять же можно легко убедиться, что минимальный урезающий фактор, который позволяет проводить надежную оценку h = N/2+p (p число независимых переменных плюс один), т.е. надежность робастной оценки опять может быть почти 50%. Собственно, с МУК все довольно просто, исключая один нетривиальный вопрос связанный с выбором h. Первый пристрелочный способ выбора можно характеризовать, как “на глазок”. Если выборка, где мы проводим регрессию не очень большая, то число выбросов можно прикинуть и урезающий фактор выбрать попробовав несколько близких значений, тем более если с уменьшеним/увеличением оценка не меняется. Однако, существуют и более строгие критерии выбора [3,4], которые, к сожалению, ведут к заметному увеличение времени счета даже в случае линейных регрессий.
Кратно перечислим другие известные эстиматоры, которые часто используются в литературе [1]:
1) least median squares (метод медианных квадратов)
2) M-, R-, S-, Q- estimators, эстиматоры основанные на некоторой оценочной функции (к примеру, МНК тоже может быть назван М-эстиматором), и
различных вариациях оценки ошибок (моменты, срезающие гиперплоскости и тд).
3) Эстиматоры для нелинейных регрессий [5]
Пункт два в этом списке является несколько неточным, потому что в одну кучу для удобства собраны многие довольно разные по своей природе эстиматоры.
В качестве простого, но очень интересного приложения робастных оценок приведем робастную оценку диффузионного тензора в ЯМР томографии [6]. В ЯМР томографии одним из интересных приложений являются диффузионные измерения на молекулах воды, которые подвержены броуновскому движению в головном мозгу. Однако, благодаря различным ограничениям (движение вдоль нейроволокон, в дендридах, внутри и вне клеток и тд) имеют разные параметры диффузии. Производя измерения в шести различных направлениях (диффузионный тензор является положительно определенным, т.е. нам нужно узнать только 6 его элементов), мы можем востановить сам тензор, через известную модель спада сигнала. Пространственные направления кодируются градиентными катушками в импульсной последовательности. Мы можем представить диффузионный тензор, как эллипсоид, получить изображение нейронных нитей в мозгу (см. например diffusion MRI в wiki

). Нити представляют собой упорядоченные тензоры, которые аппроксимируются некой кривой (через всем известный метод Рунге-Кутта). Даный подход носит название streamline [7].
Однако измерения подобного рода являются наиболее богатыми на различного рода артефакты (по сравнению с другими видами изображений) из-за биения сердца, распираторного движения грудной клетки, движения головы во время измерений, разных тиков, дрожанию стола из-за часто переключающихся магнитных градиентов и тд. Таким образом, востановленный диффузионный тензор может иметь заметные отклонения от настоящих значений и, как следствие, неверное направление в случае его ярко выраженной анизотропии. Это не позволяет использовать полученные треки нервных волокон, как надежный источник информации об устройстве нервных связей или планировать хирургические операции. В действительности, подход основанный на диффузионном тензоре не используется для востановления изображения нервных волокон, поэтому большинству пациентов можно пока не волноваться.
Математическая теория робастных эстиматоров является довольно интересной, т.к. во многих случаях основывается на уже известных подходах (это означает, что большинство строгой и сухой теории уже известно), но имеет дополнительные свойства позволяющие значительно дополнить и улучшить оценочные результаты. Если вернуться к уже упомянотому МНК, то введение весовых множителей позволяет получить робастные оценки в случае линейной регрессии. Следующий шаг изменение весовых множителей введением итераций в оценках, в итоге мы получим известный iteratively reweighted least squares approach [2].
Надеюсь читатели, незнакомые с робастной статистикой, получили некоторое представление о робастных эстиматорах, а знакомые – увидели интересные приложения своим знаниям.
Литература
1. Rousseeuw PJ, Leroy AM, Robust regression and outlier detection. Wiley, 2003.
2. Bjoerck A, Numerical methods for least squares problems. SIAM, 1996.
3. Agullo, J. New algorithm for computing the least trimmed squares regression estimator. Computational statistics & data analysis 36 (2001) 425-439.
4. Hofmann M, Gatu C, Kontoghiorghes EJ. An exact least trimmed squares algorithm for a range of coverage values. Journal of computational and graphical statistics 19 (2010) 191-204.
5. Motulsky HJ, Brown RE. Detecting outliers when fitting data with nonlinear regression – a new method based on robust nonlinear regression and the false discovery rate. BMC Bioinfromatics 7 (2006) 123.
6. Change LC, Jones DK, Pierpaoli C. RESTORE: Robust estimation of tensors by oulier rejection. Magnetic Resonance in Medicine 53 (2005) 1088-1085.
7. Jones DK, Diffusion MRI: Theory, Methods and Applications. Oxford University Press, 2010.
Во время учебы в университете курс статистики, который нам читали (а это было больше, чем 15 лет назад), был самый что ни на есть типичный: введение через теорию вероятностей и часто встречающиеся распределения. Больше в голове с тех пор про этот семестровый курс ничего не осталось. Мне кажется, что в курсе статистической физики многое дается много лучше. Уже значительно позже жизнь столкнула меня с медицинской физикой, где статистические методы являются одним из основных инструментов анализа данных, полученных, например, с помощью ЯМР томографии. Тут то я первый раз и встретил термин robust statistics и robust estimators. Сразу оговорюсь, я покажу только простые примеры применения робастных эстиматоров и дам ссылки на литературу, интересующиеся легко смогут углубить и расширить свои знания использую список литературы в конце этой заметки. Давайте разберем самый простой пример наиболее часто встречающийся, чтобы продемонстрировать надежную оценку в какой либо выборке. Предположим, что студент Вася сидит на физическом практикуме и записывает показания некоего прибора:
4.5
4.1
5.2
5.5
3.9
4.3
5.7
6.0
45
47
Прибор работает не так чтобы очень точно плюс к этому Вася отвлекается на разговоры с соседкой по практикуму Леной. Как результат в последних двух записях Василий не ставит десятичную точку и, вуаля, – мы имеет проблему.
Шаг первый, мы упорядочиваем нашу выборку по возрастанию и вычисляем среднее значение
mean = 13.12
Сразу видно, что среднее значение далеко от реального среднего благодаря двум последним выбросам (outliers), попавшим в выборку. Самый простой способ оценить среднее неучитывая влияние выбросов – это медиана
median = 5.35
Таким образом, самый простой робастный эстиматор – это медиана, действительно, мы можем видеть, что до 50% данных можно “загрязнить” разного рода выбросами, но оценка медианы не изменится. На этом простом примере можно ввести сразу несколько понятий: что такое робастность в статистике (устойчивость оценок по отношению к выбросам в данных), насколько используемый эстиматор является робастным (как сильно можно “загрязнить” данные без существенного изменения полученных оценок) [1]. Можно ли улучшить медианную оценку? Безусловно можно ввести еще более надежный эстиматор известный как абсолютное отклонение от медианы (median absolute deviation or MAD)
MAD = median(|xi-median[xj]|)
в случае нормального распределения вводят численный фактор перед MAD, позволяющий сохранить оценку без изменений. Как несложно заметить устойчивость MAD так же является 50%.
Огромное практическое применение робастные эстиматоры нашли в линейных регрессиях. В случае линейной зависимости (x,y) часто надо получить хорошо обусловленные оценки такой зависимости (часто в случае мультивариативной регрессии)
y = Bx +E ,
где B уже может представлять собой матрицу коэффициентов, Е некий шум, портящий наши измерения, и x набор параметров (вектор), который мы собственно и хотим оценить, используя измерянные значения y (вектор). Самый простой и всем известный способ это сделать – это метод наименьших квадратов (МНК) [2]. В принципе, очень легко убедиться, что МНК робастным эстиматором не является и его робастная надежность равна 0%, т.к. даже один выброс может существенно изменить оценку. Один из самых математических красивых трюков, позволяющий улучшить оценку, называется least trimmed squares или метод “урезанных” квадратов (МУК). Его идея заключается в тривиальной модификации оригинального МНК, в которой урезают число используемых оценок, т.е.:
оригинальный МНК
min \sum_{i=1}^N r_i^2, МУК
min \sum_{i=1}^h {r_i^2}_{1:N}, где r_i это уже упорядоченные ошибки оценок (y – O(x)), т.е. r_1<r_2<...<r_N. Опять же можно легко убедиться, что минимальный урезающий фактор, который позволяет проводить надежную оценку h = N/2+p (p число независимых переменных плюс один), т.е. надежность робастной оценки опять может быть почти 50%. Собственно, с МУК все довольно просто, исключая один нетривиальный вопрос связанный с выбором h. Первый пристрелочный способ выбора можно характеризовать, как “на глазок”. Если выборка, где мы проводим регрессию не очень большая, то число выбросов можно прикинуть и урезающий фактор выбрать попробовав несколько близких значений, тем более если с уменьшеним/увеличением оценка не меняется. Однако, существуют и более строгие критерии выбора [3,4], которые, к сожалению, ведут к заметному увеличение времени счета даже в случае линейных регрессий.
Кратно перечислим другие известные эстиматоры, которые часто используются в литературе [1]:
1) least median squares (метод медианных квадратов)
min median r_i^2 2) M-, R-, S-, Q- estimators, эстиматоры основанные на некоторой оценочной функции (к примеру, МНК тоже может быть назван М-эстиматором), и
различных вариациях оценки ошибок (моменты, срезающие гиперплоскости и тд).
3) Эстиматоры для нелинейных регрессий [5]
Пункт два в этом списке является несколько неточным, потому что в одну кучу для удобства собраны многие довольно разные по своей природе эстиматоры.
В качестве простого, но очень интересного приложения робастных оценок приведем робастную оценку диффузионного тензора в ЯМР томографии [6]. В ЯМР томографии одним из интересных приложений являются диффузионные измерения на молекулах воды, которые подвержены броуновскому движению в головном мозгу. Однако, благодаря различным ограничениям (движение вдоль нейроволокон, в дендридах, внутри и вне клеток и тд) имеют разные параметры диффузии. Производя измерения в шести различных направлениях (диффузионный тензор является положительно определенным, т.е. нам нужно узнать только 6 его элементов), мы можем востановить сам тензор, через известную модель спада сигнала. Пространственные направления кодируются градиентными катушками в импульсной последовательности. Мы можем представить диффузионный тензор, как эллипсоид, получить изображение нейронных нитей в мозгу (см. например diffusion MRI в wiki
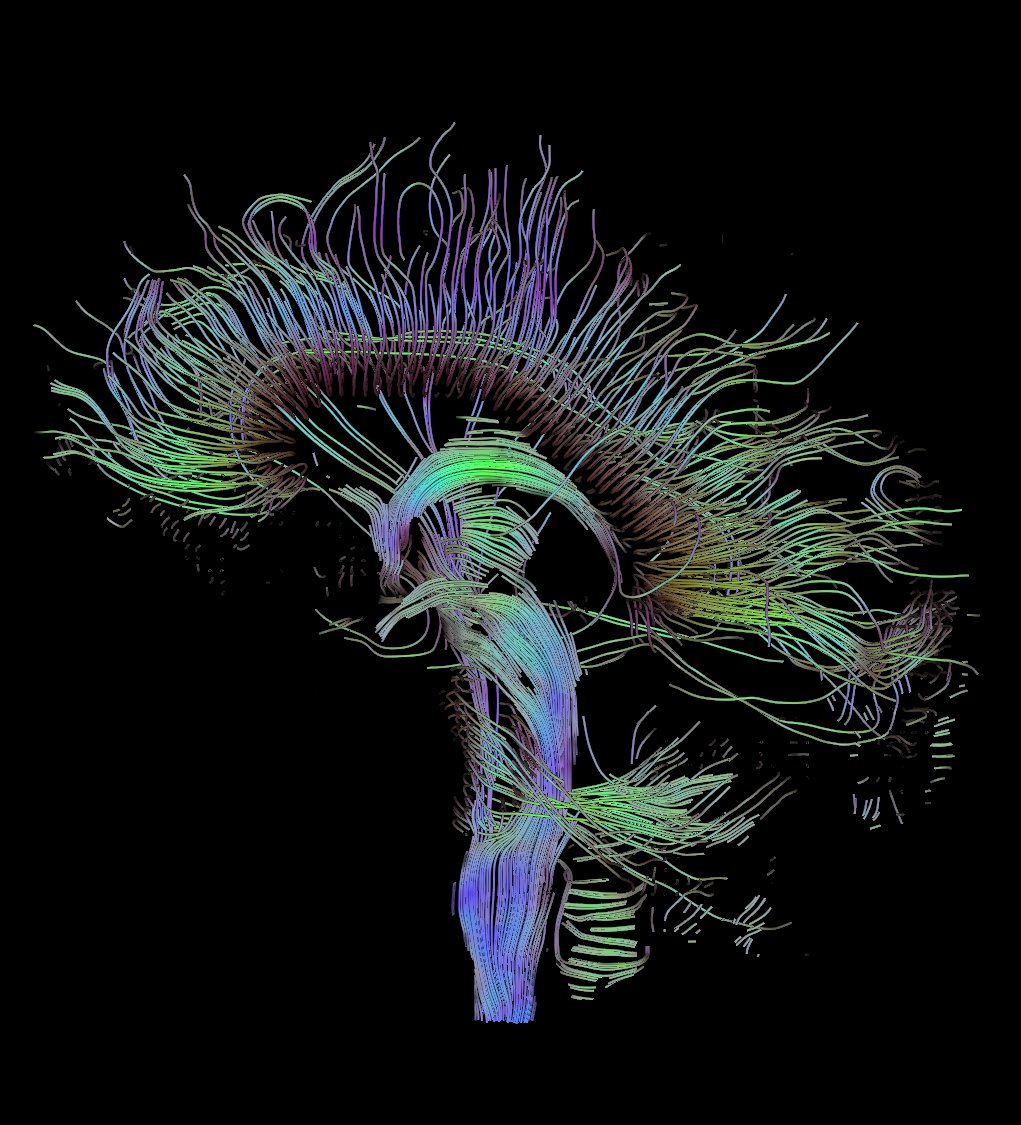
). Нити представляют собой упорядоченные тензоры, которые аппроксимируются некой кривой (через всем известный метод Рунге-Кутта). Даный подход носит название streamline [7].
Однако измерения подобного рода являются наиболее богатыми на различного рода артефакты (по сравнению с другими видами изображений) из-за биения сердца, распираторного движения грудной клетки, движения головы во время измерений, разных тиков, дрожанию стола из-за часто переключающихся магнитных градиентов и тд. Таким образом, востановленный диффузионный тензор может иметь заметные отклонения от настоящих значений и, как следствие, неверное направление в случае его ярко выраженной анизотропии. Это не позволяет использовать полученные треки нервных волокон, как надежный источник информации об устройстве нервных связей или планировать хирургические операции. В действительности, подход основанный на диффузионном тензоре не используется для востановления изображения нервных волокон, поэтому большинству пациентов можно пока не волноваться.
Математическая теория робастных эстиматоров является довольно интересной, т.к. во многих случаях основывается на уже известных подходах (это означает, что большинство строгой и сухой теории уже известно), но имеет дополнительные свойства позволяющие значительно дополнить и улучшить оценочные результаты. Если вернуться к уже упомянотому МНК, то введение весовых множителей позволяет получить робастные оценки в случае линейной регрессии. Следующий шаг изменение весовых множителей введением итераций в оценках, в итоге мы получим известный iteratively reweighted least squares approach [2].
Надеюсь читатели, незнакомые с робастной статистикой, получили некоторое представление о робастных эстиматорах, а знакомые – увидели интересные приложения своим знаниям.
Литература
1. Rousseeuw PJ, Leroy AM, Robust regression and outlier detection. Wiley, 2003.
2. Bjoerck A, Numerical methods for least squares problems. SIAM, 1996.
3. Agullo, J. New algorithm for computing the least trimmed squares regression estimator. Computational statistics & data analysis 36 (2001) 425-439.
4. Hofmann M, Gatu C, Kontoghiorghes EJ. An exact least trimmed squares algorithm for a range of coverage values. Journal of computational and graphical statistics 19 (2010) 191-204.
5. Motulsky HJ, Brown RE. Detecting outliers when fitting data with nonlinear regression – a new method based on robust nonlinear regression and the false discovery rate. BMC Bioinfromatics 7 (2006) 123.
6. Change LC, Jones DK, Pierpaoli C. RESTORE: Robust estimation of tensors by oulier rejection. Magnetic Resonance in Medicine 53 (2005) 1088-1085.
7. Jones DK, Diffusion MRI: Theory, Methods and Applications. Oxford University Press, 2010.