
Хайп прошёл, а что осталось?
Как обычно, в поиске, но hr-девицы, не читая резюме, пытаются переспросить.
Чтобы бороться с этом решил автоматизировать общение с ними, выводя их на общение с ботом.
Граф О'ман

Хайп прошёл, а что осталось?
Как обычно, в поиске, но hr-девицы, не читая резюме, пытаются переспросить.
Чтобы бороться с этом решил автоматизировать общение с ними, выводя их на общение с ботом.

Алгориитм Шора — квантовый алгоритм факторизации (разложения числа на простые множители), позволяющий разложить число M за время O((logM)^3) используя O(log M) логических кубитов.
Алгоритм Шора был разработан Питером Шором в 1994 году. Семь лет спустя, в 2001 году, его работоспособность была продемонстрирована группой специалистов IBM. Число 15 было разложено на множители 3 и 5 при помощи квантового компьютера с 7 кубитами.
Алгоритм Шора состоит из 2-х частей - квантовых и классических вычислений.
Квантовая часть алгоритма отвечает за определение периода функции с помощью квантовых вычислений.
Классические вычисления решают задачу как по найденному периоду степенной функции найти разложение на сомножители.
Практически, схема этого алгоритма полностью повторяет схему алгоритма Саймона, с отличием в последнем шаге - вместо применения оператора Адамара перед измерением входного регистра, используется оператор преобразования Фурье.
А какие есть ещё варианты определить период функции используя квантовые вычисления?
Когда-то ранее я писал статьи про способы сравнения (поиска фрагмента) изображений, поиска частоты сердечных сокращений с использованием операции вычисления скалярного произведения, которую я делал с помощью свёртки на основе БФП.
• Фурье-вычисления для сравнения изображений
а так же начал повторять эту технологию при квантовых вычислениях
• Изучаем Q#. Алгоритм Гровера. Не будите спящего Цезаря
Так почему бы не повторить успешный успех и, заодно, обобщить теорию вопроса?

Как и бит, кубит допускает два собственных состояния, обозначаемых |0> и |1> (обозначения Дирака), но при этом может находиться и в их суперпозиции.
В общем случае его волновая функция имеет вид A|0>+B|1>, где A и B называются амплитудами вероятностей и являются комплексными числами, удовлетворяющими условию |A|^2+|B|^2=1 (но это не обязательно соблюдать при записи - всегда подразумевается, что происходит нормирование величин).
При измерении состояния кубита можно получить лишь одно из его собственных состояний.
Вероятности получить каждое из них равны соответственно |A|^2 и |B|^2.
Как правило, при измерении состояние кубита необратимо разрушается, чего не происходит при измерении классического бита.
В квантовых вычислениях, мы имеем факт, что применение трансформации Адамара H к кубиту в состоянии |0> даёт нам его в равновероятном состоянии для исходов |0> и |1>, то есть в состоянии |0>+|1>
Но как нам задать нужное состояние кубита, то есть с заранее заданными значениями A и B ?
Вернее, как задать нужное состояние кубита, используя только минимальный набор базовых операций? Ведь любой QDK должен включать в себя методы инициализации кубита (и желательно в требуемом состоянии).
Ну а мы ограничимся в данном примере операциями H и Controlled X.

Базовым элементом построения нейросетей, как мы знаем, является модель нейрона, а, соответственно, простейшей моделью нейрона, является перцептрон.
С математической точки зрения, перцептрон решает задачу разделения пространства признаков гиперплоскостью, на две части. То есть является простейшим линейным классификатором.
Обобщенная схема нейрона представляет собой функцию f(SUM Wi*xi - W0)
Здесь:
• x1,...,xn – компоненты вектора признаков x=(x1,x2,...,xn);
• SUM – сумматор;
• W1,W2,...,Wn – синоптические веса;
• f – функция активации; f(v)= { 0 при v < 0 и 1 при v>0 }
• W0 – порог.
Таким образом, нейрон представляет собой линейный классификатор с дискриминантной функцией g(X)=f(SUM Wi*Xi - W0).
И задача построения линейного классификатора для заданного множества прецедентов (Xk,Yk) сводится к задаче обучения нейрона, т.е. подбора соответствующих весов W1,W2,...,Wn и порога W0.
Классический подход обучения перцептрона хорошо известен
• Инициализируем W0,W1,W2,...Wn (обычно случайными значениями)
• Для обучающей выборки (Xk,Yk) пока для всех значений не будет выполняться f(SUM Wi*Xki - W0)==Yi повторяем последовательно для всех элементов
• W = W + r(Yk - f(SUM Wi*Xki - W0)) * Xk*, где 0 < r < 1 - коэффициент обучения
Для доказательства сходимости алгоритма применяется теорема Новикова, которая говорит, что если существует разделяющая гиперплоскость, то она может быть найдена указанным алгоритмом.
Что же нам может предложить модель квантовых вычислений для решения задачи обучения перцептрона - то есть для нахождения синоптических весов по заданной обучающей выборке?
Ответ - мы можем сразу опробовать все возможные значения весов и выбрать из них тот - который удовлетворяет нашим требованиям - то есть правильно разделяет обучающую выборку.
Для понимания данного туториала вам потребуются базовые знания по
• нейросетям
• квантовым вычислениям (кубиты и трансформации)
• программированию на Q-sharp

Почему так бывает, что люди, считающие себя учёными и проводящие днём слепое исследование, придя вечером домой читают гороскоп?
Если ты смотришь на мир через призму науки - то почему бы и на себя не взглянуть?
Сказано - сделано: построим графики своей активности на хабре.

Добро пожаловать в новый мир новых технологий вычислений!
В быту, когда мы смотрим на разные предметы, мы пытаемся понять - похожи ли они или нет, и на сколько они похожи.
Так и в математике - когда мы смотрим на последовательностей чисел, мы пытаемся понять - похожи ли они или нет, и насколько они похожи.
Одним из таких критериев "похожести" является совпадение частотных характеристик этих последовательностей.
Рассмотрим вопрос, как реализовать такую проверку с использованием квантовых вычислений и напишем программку-тест на Q-sharp для проверки этих рассуждений.
Для понимания данного туториала вам потребуются базовые знания по
теории вероятности
алгебре
булевым функциям
свёртке, корреляции, скалярному произведению
квантовым вычислениям (кубиты и трансформации)
программированию на Q-sharp
Криптохомячкам посвящается ...
Алгоритм Гровера представляет собой обобщённый, независящей от конкретной задачи поиск, функция которого представляет "чёрный ящик" f: {0,1}^n to {0,1}^n, для которой известно, что EXISTS!w:f(w)=a, где a — заданное значение.
Считаем, что для f и заданного a можно построить оракул Uf: { |w> to |1>, |x> to |0> if |x> != |w> }

Применим этот алгоритм для решения задачи нахождения ключа шифра Цезаря ...

Биномиальное распределение с параметрами n и p в теории вероятностей — распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна p.
Рассмотрим случай, когда p=0.5 - это делается только для упрощения примера.
В этом случае, согласно теории, вероятность выпадения исхода k на вероятностном пространстве из целых чисел равно P(k)=C(k,n)/2**n, где C(k,n) = n!/(k!(n-k)!) - коэффициент бинома Ньютона.
Поставим перед собой цель - сформировать в массиве кубитов, который мы будем рассматривать как регистр из нескольких кубитов, состояние SUM SQRT(C(k,n))|k>

Алгоритм Дойча — алгоритм, разработанный Дойчем в 1985 году, и ставший одним из первых квантовых алгоритмов. В нём рассматривается функция булевая f(x) от одной переменной и требуется определить является ли она постоянной или сбалансированной.
Что нам говорит Википедия?
Алгоритму Дойча — Йожи достаточно однократного обращения к квантовому оракулу для достоверного решения задачи.
А джентельменам принято верить на слово, значит решим эту задачу, как первый опыт программирования на Q# ...
При обработке медицинских данных требуется определять частоту сердечных сокращений (ЧСС). Большинство методик расчёта ЧСС использует определение пиков в графике сердечных сокращений и подсчёта длительности интервала между пиками. Альтернативным методом расчёта ЧСС является вычисление корреляции последовательности измерений относительно сдвига графика на заданный интервал времении и выбор в качестве вычисленного интервала того, при котором корреляция максимальная. Недостатком вычисления интервала сердечных сокращений методом рассчёта корреляции является большое число вычислений, однако число этих расчётов можно существенно сократить при использовании быстрых Фурье преобразований (БФП).
С целью освоения библиотек для работы с нейронными сетями, решим задачу аппроксимации функции одного аргумента используя алгоритмы нейронных сетей для обучения и предсказания.

Пример: некоторую функцию очень дорого вычислять для каждого значения аргументов (а их много, допустим N) — поэтому строится таблица значений и при необходимости получения значения функции в определенной точке — интерполируется по табличке. Разумеется, изначальное построение таблицы и процедура интерполирования (N раз) должны быть «дешевле», чем точное вычисление самой функции N раз.
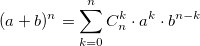 также использует биномиальные коэффициенты. Для их расчета можно использовать формулу, выражающую биномиальный коэффициент через факториалы:
также использует биномиальные коэффициенты. Для их расчета можно использовать формулу, выражающую биномиальный коэффициент через факториалы: 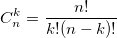 или использовать рекуррентную формулу:
или использовать рекуррентную формулу: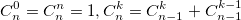 Из бинома Ньютона и рекуррентной формулы ясно, что биномиальные коэффициенты — целые числа.
Из бинома Ньютона и рекуррентной формулы ясно, что биномиальные коэффициенты — целые числа. d(X,Y) = SUM ( X[i,j] — Y[i,j] )^2