Comments 68
Как известно, есть правда, есть ложь, а есть статистика. Вечная истина.
0
Я слышал в более жестком варианте: «Есть три вида лжи: ложь, наглая ложь и статистика».
+21
Поправочка:
Существуют три вида лжи: ложь, наглая ложь и статистика. (Марк Твен)
Но мне больше по нраву:
По статистике один пешеход попадает под колеса автомобиля каждые 17 минут. Бедняга! (Янина Ипохорская)
Существуют три вида лжи: ложь, наглая ложь и статистика. (Марк Твен)
Но мне больше по нраву:
По статистике один пешеход попадает под колеса автомобиля каждые 17 минут. Бедняга! (Янина Ипохорская)
+16
Здорово! То, что доктор прописал для презентации по моей бакалаврской =)
Благодарю за информацию!
Благодарю за информацию!
0
Учтите, что в третьем и дальнейших знаках некоторые значения на самом деле не равны.
0
Само собой, но оживить презентацию эта информация способна :)
А то сплошные формулы, код, графики… надо было попроще брать тему…
А то сплошные формулы, код, графики… надо было попроще брать тему…
0
Здесь дело не в знаке, можно подобрать точки так, чтобы значения были в точности равны, а картинки выглядели так же. Эти картинки нам просто показывают, что статистическая информация — это просто усреднение, которое часто не отражает реальную природу данных.
0
Скажем так: нельзя ограничиваться несколькими статистическими показателями без подробного анализа данных.
Особенно это касается любимого всеми коэффициента корреляции: постоянно забывают, особенно всякие журналисты, что статистическая взаимосвязь не означает причинно-следственную взаимосвязь.
Классический пример:
Особенно это касается любимого всеми коэффициента корреляции: постоянно забывают, особенно всякие журналисты, что статистическая взаимосвязь не означает причинно-следственную взаимосвязь.
Классический пример:

+16
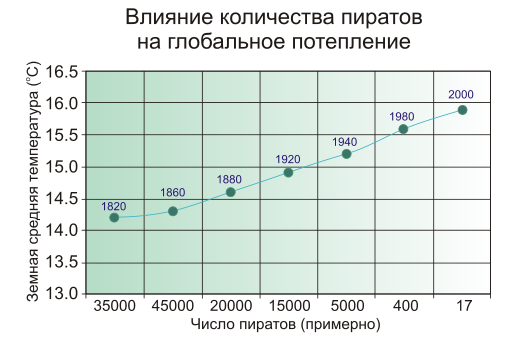
Люди, которые делают утреннюю зарядку, умирают в сто раз реже остальных. Потому что их в сто раз меньше, чем остальных.
+21
UFO just landed and posted this here
Пресвятые макароны!
+6
О причинной связи можно говорить, если в эксперименте искуственно меняется одна переменная, а при этом наблюдается изменения в другой. Тогда коэффициент корреляции действительно покажет причинную связь
0
*занудство* как то у вас по оси Х странно циферки расположены. Потому и график не верен
0
+1
Первая мысль, когда посмотрел на C и D, что данные находятся в более, чем 2-мерном пространстве Оо
0
отклонения больше чем 3сигмы выкидываются из результатов эксперимента, некоторые точки я бы под сомнение поставил
+3
А где здесь эксперимент? ;)
0
А с чем оперирует статистика? Только с эксперементальными данными.
+5
Здесь данные, конечно, не экспериментальные, а так — чистая игра ума. Как раз для того, чтобы показать уровень доверия к обобщенным показателям.
Впрочем, правило трёх сигм применяется только к нормально распределенным данным, а это ведь далеко не все возможные случаи. Например, размер зарплат у населения России — величина отнюдь не нормально распределенная.
И ещё: в квартете Анскомбе все данные, кроме случая D, вписываются в интервал трех сигм. И даже вон та зависшая точка в D — тоже почти на краю, ну чуть-чуть выбивается :)
Впрочем, правило трёх сигм применяется только к нормально распределенным данным, а это ведь далеко не все возможные случаи. Например, размер зарплат у населения России — величина отнюдь не нормально распределенная.
И ещё: в квартете Анскомбе все данные, кроме случая D, вписываются в интервал трех сигм. И даже вон та зависшая точка в D — тоже почти на краю, ну чуть-чуть выбивается :)
+1
в хлс файле все формулы явно для нормального распределения.
-2
Хмм… в общем случае можно использовать неравенство Чебышева, нет?
Оно хотя не такое сильное, как правило трех сигм для нормального, но тоже не слишком слабое.
Оно хотя не такое сильное, как правило трех сигм для нормального, но тоже не слишком слабое.
0
Для борьбы с точками-«аутсайдерами» (laverage effect) обычно применяют статистические критерии, например Q-тест
+1
Сумма одинаково распределенных величин в пределе имеет нормальное распределение. Центральная предельная теорема.
Даже сумма четырех-пяти равномерно распределенных величин (плотность — прямая линия) визуально очень сильно напоминает гауссиану.
Даже сумма четырех-пяти равномерно распределенных величин (плотность — прямая линия) визуально очень сильно напоминает гауссиану.
+1
Статистикой не обязательно анализируются данные некоего физического эксперимента, предполагающего устойчивое поведение. Это могут быть данные соцопроса, замеры качества деталей и т.п. «Правило трех сигм» тут не применимо.
0
UFO just landed and posted this here
Именно поэтому в экспериментальной физике никогда не смотрят на выведенные зависимости без приложенных к ним «сырых» результатов.
+1
У меня такое ощущение, что вы только что сказали — «Земля плоская! Потому-что я не вижу что она круглая.». Если вы конечно серьёзно а не юморите, вот англичанин точно прикалывался.
0
Дополнение от друга:
Автор, он намекает, что показатели статистические ничего конкретного о выборке не говорят. и как следствие — методология статистики типа ебанутая. на самом деле эти примеры демонстрируют очень важную хрень — эти характеристики без контекста вообще не нужны. а уж линейная функция тут вообще ни при чем )))
Так что это просто лулз не больше. И гениальности тут ноль.
Автор, он намекает, что показатели статистические ничего конкретного о выборке не говорят. и как следствие — методология статистики типа ебанутая. на самом деле эти примеры демонстрируют очень важную хрень — эти характеристики без контекста вообще не нужны. а уж линейная функция тут вообще ни при чем )))
Так что это просто лулз не больше. И гениальности тут ноль.
-1
UFO just landed and posted this here
Не хватает показателей эксцесса, асимметрии, R2 — коэффициента детерминации для уравнения корреляции.
+5
Не надо портить красивую штуку :))
+4
R-квадрат совпадает с точностью до сотых. 0.666
Если использовать регрессию из пакета анализа экселя — то все показатели практически совпадают. Расхождение в сотых или тысячных
На счёт эксцесса и ассиметрии — разве они применимы в этом случае? Я что то сейчас не могу вспомнить.
Если использовать регрессию из пакета анализа экселя — то все показатели практически совпадают. Расхождение в сотых или тысячных
На счёт эксцесса и ассиметрии — разве они применимы в этом случае? Я что то сейчас не могу вспомнить.
+2
Экцесс, ассиметрия для проверки нормальности распределения. Ну, они точно будут различаться. Видно по графикам.
0
Я просто не могу сообразить, как коэффициенты асимметрии и эксцесса использовать для 2хмерной случайной величины( т.к. у нас есть x и y).
Если по отдельности считать для x и для y — то они конечно не совпадут.
Если по отдельности считать для x и для y — то они конечно не совпадут.
+1
Да, вы правы. Здесь это неуместно.
0
Вообще то можно www.tau.ac.il/cc/pages/docs/sas8/stat/chap19/sect35.htm
0
Эти графики используются как раз для того, чтобы доказать, что R^2, которое любят приводить для подтверждения связи наблюдаемых явлений в экономике (Левитт с его Freakonimics как пример) еще ни о чем не говорит :)
+1
ну это же математика, что тут удивляться? она просто режет правду матку, а её можно крутить как хочешь в зависимости что нужно достичь
+1
Ну а что вы хотели, четко описать люббую последовательность пятью параметрами? Тем более, видно что корелляция довольно адекватно описывает зависимость)
-1
То есть вы хотите сказать, что для всех 4 выборок линейная модель адекватна?
Слабо верится. :)
Слабо верится. :)
0
Как раз наоборот — совсем неадекватна.
При коэффициенте корреляции меньше 0.9 вообще нельзя приближение линейное использовать. А тут — 0.82
А лучше, конечно r>0.9
Хотя я всерьёз видел кое-какие социологически-психологические исследования, опубликованные и всё такое, гед какие-то выводы делались на основе коэффициента корреляции порядка 0.7
Вот именно этим людям квартет и надо показывать
При коэффициенте корреляции меньше 0.9 вообще нельзя приближение линейное использовать. А тут — 0.82
А лучше, конечно r>0.9
Хотя я всерьёз видел кое-какие социологически-психологические исследования, опубликованные и всё такое, гед какие-то выводы делались на основе коэффициента корреляции порядка 0.7
Вот именно этим людям квартет и надо показывать
0
На мой взгляд A,B,C весьма похожи, что и проявляется в схожести параметров.
Если добавить median то D сразу станет в стороне.
Вообще median зачастую дает более полезную информацию, чем среднее (арифметическое) напр. для средней зар. платы.
Если добавить median то D сразу станет в стороне.
Вообще median зачастую дает более полезную информацию, чем среднее (арифметическое) напр. для средней зар. платы.
+3
Не надо морочить людям голову. Четыре представленных параметра характеризуют эти случайные величины очень слабо. Можно сравнить с четырьмя последними цифрами crc32 суммы для некоторых двух медиафайлов. Вообще говоря, без курса тервера упоминание матстата в принципе бессмысленно, а процесс его понимания может взорвать мозг на приличный промежуток времени (где-то два месяца если самому изучать).
0
Да, линейная регрессия, которую так любят в экономике и, особенно, социологии довольно опасная вещь.
Часто любят писать про коэффициенты корреляции наборов статданных, но реально там может быть ничего обещего. Большая проблема для оценки качества научной работы…
Часто любят писать про коэффициенты корреляции наборов статданных, но реально там может быть ничего обещего. Большая проблема для оценки качества научной работы…
0
Для случая B надо было использовать нелинейную регрессию, в остальных случаях — просто исключить ту точку, где отклонение наибольшее. А вот если бы взяли реальную статистическую выборку (хотя-бы 1000 значений x), то и исключать ничего не надо было бы.
+2
Ну тогда A можно описать, как линия + периодическая функция ( достаточно просто для 3х точек задать значение).
B — многочленом 2-ого или 3-его порядка.
С — выбросить одну точку и сказать, что это ошибочное измерение.
D — выбросить крайнюю точку. И подогнать y под какое-нибудь распределение случайной величины.
Но прикол не в этом. Да и выборка маленькая.
B — многочленом 2-ого или 3-его порядка.
С — выбросить одну точку и сказать, что это ошибочное измерение.
D — выбросить крайнюю точку. И подогнать y под какое-нибудь распределение случайной величины.
Но прикол не в этом. Да и выборка маленькая.
+1
UFO just landed and posted this here
Из-за того что подобные наблюдения статистиков часто публикуются без адекватного комментария, в массах и формируется базовое недоверие к математической статистике вообще. Это лишь иллюстрация к тому, что при использовании всякого средства нужно представлять его возможности, ограничения и допущения, которые лежат в их основе.
-1
Корреляция описывает линейную зависимость между данными, которой здесь и не пахнет.
Собственно, по ссылке в википедии всё написано.
При том, что этот факт в общем-то хорошо известен, эту самую ошибку многие повторяют с завидным постоянством.
Есть мнение, что недавний кризис (который начался с обвала subprime ипотеки в США) начался с похожей ошибки: оригинальная статья (англ)
Собственно, по ссылке в википедии всё написано.
При том, что этот факт в общем-то хорошо известен, эту самую ошибку многие повторяют с завидным постоянством.
Есть мнение, что недавний кризис (который начался с обвала subprime ипотеки в США) начался с похожей ошибки: оригинальная статья (англ)
0
Среднее значение и дисперсия однозначно характеризуют набор данных, только если его распределение хорошо моделируется нормальным, а остальных случаях нужны ещё параметры, вроде их штук пять в сумме надо, деталей не помню.
0
Sign up to leave a comment.
Квартет Анскомбе