Математики с давних времён пытались решить задачу о пасущейся козе, привязанной к изгороди. Но до настоящего времени они могли предложить только приблизительные решения.

Вот вам простая на первый взгляд задачка. Представьте себе изгородь в форме окружности, с точно известной площадью пастбища, заключённого внутри. Внутрь вы помещаете козу, и привязываете её верёвкой к изгороди. Какой длины верёвка вам понадобится, чтобы у козы был доступ ровно к половине этой площади?
Похоже на задание по геометрии для старших классов – однако профессиональные математики и любители думали над ней в разных формулировках более 270 лет. Некоторые варианты этой задачи были успешно решены, однако загадка про козу внутри круга до сих пор не давала нам ничего кроме размытых и неполных ответов.
По сей день «никто не знал точного ответа на базовый вопрос», — сказал Марк Мейерсон, математик из академии военно-морского флота США. «Решение всегда было приблизительным».
Однако в 2020-м году немецкий математик Инго Уллиш, наконец, достиг прогресса. Он нашёл, как считается, первое точное решение этой задачи – хотя и выглядит оно достаточно громоздко и непонятно.
«Это первое точное выражение для длины верёвки из всех, что я знаю», — сказал Майкл Харрисон, математик из университета Карнеги-Меллона. «Это определённо прорыв».
Уллиш признаёт, что его решение не будет перечёркивать учебники или устраивать математические революции. Эта задача является изолированной. «Она не связана с другими задачами, и не входит в какую-нибудь математическую теорию». Но всегда есть вероятность, что подобная загадка породит какие-нибудь новые математические идеи, или поможет исследователям найти иные подходы к другим задачам.
На скотном дворе и вокруг него
Первую задачу подобного типа опубликовали 1748 году в лондонском периодическом женском журнале The Ladies Diary: Or, The Woman’s Almanack [Дневник леди, или Женский альманах]. Журнал обещал «новые улучшения в искусствах и науках и множество занимательных мелочей».
В оригинальном сценарии участвует лошадь, пасущаяся на привязи в парке. В задаче лошадь была привязана снаружи ограды. Если длина верёвки совпадает с длиной окружности ограды, на какой области сможет пастись лошадь? Позднее эту задачу назвали «наружной», поскольку в ней пастбище находилось не внутри окружности, а снаружи.

Ответ на задачку появился в выпуске от 1749 года. Ответ составил некто «мистер Хит», на основании, среди прочего, справочника «исследования и таблицы логарифмов». Он дал ответ: 76 257,86 квадратных ярдов при верёвке длиной в 160 ярдов. И это был приблизительный ответ, а не точный расчёт. Поясним на примере: к уравнению x2 − 2 = 0 можно написать примерный численный ответ, x = 1,4142, но это будет не такой точный или удовлетворительный результат, как x = √2.
Вновь задача появилась в 1894 году в первом номере ежемесячника American Mathematical Monthly, переделанная для случая, когда животное пасётся внутри ограды. Такой тип задач называют «внутренними», и в среднем они сложнее внешних, пояснил Уллиш. Во внешней задаче можно отталкиваться от радиуса круга и длины верёвки, после чего подсчитать площадь. Она решается через интегралы.
«Решить её в обратном направлении, начав с заданной площади, и поставив вопрос о том, какие входные данные к ней приводят, гораздо труднее», — сказал Уллиш.
В последовавшие десятилетия в ежемесячнике публиковали разные варианты внутренней задачи, в основном с участием лошадей (и, по меньшей мере, в одном случае – с мулом) вместо коз. Ограды там фигурировали круглые, квадратные и эллиптические. Но в 1960-х годах по загадочным причинам козы начали постепенно вытеснять лошадей в литературе. Несмотря на то, что по утверждению математика Маршалла Фрейзера, козы «слишком независимы для того, чтобы жить на привязи».
Козы в высших измерениях
В 1984 году Фрейзер проявил творческий подход, выведя задачу из плоской пасторальной темы на более сложный ландшафт. Он подсчитал, какой длины понадобится верёвка, чтобы коза смогла пастись ровно в половине объёма n-мерной сферы при приближении n к бесконечности. Мейерсон нашёл в его рассуждениях логическую ошибку и позже в том же году исправил её, но пришёл к тому же выводу. При приближении n к бесконечности отношение длины верёвки к радиусу сферы стремится к √2.
Мейерсон отметил, что такой, вроде бы более сложный способ описания задачи, в многомерном пространстве вместо поля с травой, на самом деле облегчил поиск решения. «В бесконечном количестве измерений у нас есть точный ответ, а в двух измерениях такого ясного решения не существует».
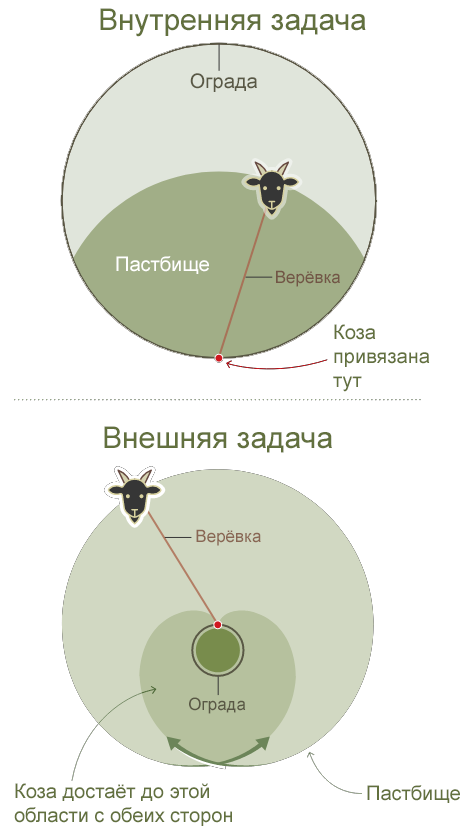
Задач о пасущейся козе бывает два вида. Оба они связаны с козой, привязанной к круглой ограде. Внутренняя версия задаёт вопрос о длине верёвки, которая даст доступ ровно к половине окружённой площади. Внешняя спрашивает, к какой площади есть доступ у козы при заданной длине верёвки и радиусе ограды (на рисунке длина верёвки равна длине окружности ограды).
В 1998 году Майкл Хоффман, ещё один математик из военно-морской академии США, расширил задачу в другом направлении, наткнувшись на пример внешней задачи в одной из новостных групп. В том её варианте нужно было оценить площадь, доступную быку, привязанному снаружи круглой силосной башни. Задача заинтересовала Хоффмана, и он решил обобщить её не только на круг, но на любую гладкую выпуклую кривую, включая эллипсы и даже незамкнутые кривые.
«Встретив постановку задачи для простого случая, математик попытается понять, как её можно обобщить», — сказал Хоффман.
Хоффман рассмотрел случай, в котором привязь длины L меньше или равна половине длины кривой. Сначала он нарисовал касательную в том месте, где привязана верёвка. Бык может пастись в полукруге площадью πL2/2, ограниченном касательной. Затем Хоффман подсчитал точную площадь между касательной и кривой через интеграл.
Позднее Грэхем Джеймсон, математик из университета Ланкастера, и его сын Николас вывели подробное решение внутренней задачи для трёх измерений. Они выбрали этот случай потому, что он был не таким популярным. Поскольку козы не могут так легко перемещаться в трёх измерениях, Джеймсоны назвали эту задачу «задачей птицы» в работе 2017 года. Звучит она так: если привязать птицу к сферической клетке, какой длины должна быть верёвка, чтобы ограничить её перемещение ровно половиной объёма?
«Задачу в трёх измерениях на самом деле проще решать, чем в двух», — сказал Джеймсон-старший. В итоге парочка вывела точное решение. Однако, поскольку математический вид ответа получился, по словам Джеймсона, «точным, но ужасным», и мог отпугнуть неопытных исследователей, они также придумали метод приблизительных расчётов, дающий численную оценку длины верёвки, что «больше понравится любителям птиц».
Достать козу
Тем не менее, точное решение двумерной задачи в формулировке 1894 года ускользало от математиков – до появления в 2020-м работы Уллиша. Впервые об этой задаче Уллиш услышал от родственника в 2001 году, будучи ещё ребёнком. Работать над ней он начал в 2017 году, получив докторскую степень в Вестфальском университете имени Вильгельма в Мюнстере. Он решил попробовать новый подход.
К тому времени было хорошо известно, что задачу о козе можно свести к единому трансцендентному уравнению, в которое по определению входят тригонометрические члены, вроде синуса и косинуса. Это могло создать проблему, поскольку многие трансцендентные уравнения не поддаются решению. К примеру, у уравнения x = cos(x) нет точных решений.

Инго Уллиш
Однако Уллиш сформулировал задачу так, чтобы обеспечить себе более податливое трансцендентное уравнение: sin(β) – β cos(β) − π/2 = 0. И хотя оно тоже может показаться недоступным, он понял, что к нему можно подступиться при помощи комплексного анализа – ветви математики, применяющей аналитические инструменты к уравнениям с комплексными числами. Комплексный анализ применяется уже несколько столетий, однако Уллиш, насколько ему известно, первым применил такой подход к голодным козам.
С такой стратегией он смог превратить своё трансцендентное уравнение в эквивалентное выражение для длины верёвки, которая позволила бы козе пастись в половине ограниченной площади. То есть, он, наконец, ответил на вопрос при помощи точных математических формул.

Решение задачи даётся в виде косинуса отношения двух криволинейных интегралов (формула из Википедии)
К сожалению, тут есть подвох. Решение Уллиша – это не какое-то простое выражение вроде квадратного корня из 2. Это такая сложная штука, как отношение двух криволинейных интегралов с примесью различных тригонометрических функций. С практической точки зрения оно не скажет вам точно, какой длины должна быть привязь козы. Для получения ответа, применимого в сельском хозяйстве, всё равно требуется сделать несколько приближённых вычислений.
Но Уллиш всё равно считает точное решение ценным, пусть оно и не такое красивое и простое. «Если мы будем использовать только числовые значения или приближения, мы так и не поймём сути природы решения», — сказал он. «Формула даёт нам понимание того, как выводится решение».
Не отказываться от козы
Пока что Уллиш отложил в сторону пасущуюся козу, поскольку не уверен, куда двигаться дальше. Но другие математики уже развивают собственные идеи. Харрисон, например, готовит работу для публикации в Mathematics Magazine, где исследует свойства сферы, чтобы подступиться к трёхмерному обобщению задачи про козу.
«В математике часто бывает полезным придумывать новые способы получения ответа – даже для задач, уже решённых ранее, — отметил Мейерсон, — поскольку, возможно, всё это можно будут обобщить для использования в других задачах».
Именно поэтому математики потратили столько чернил на воображаемых животных. «Мои инстинкты говорят, что работа над задачей о пасущейся козе не даст нам никаких прорывов, — сказал Харрисон, — но наверняка знать нельзя. Новая математика может появиться откуда угодно».
Хоффман более оптимистичен. «Трансцендентное уравнение, выведенное Уллишем, связано с трансцендентными уравнениями, которые Хоффман изучал в работе 2017 года. Он же, в свою очередь, заинтересовался ими благодаря работе 1953 года, где общепринятые методы были выставлены в новом свете. Этот подход напоминает ему то, как Уллиш применил известные методы в комплексном анализе к трансцендентным уравнениям в новых условиях – в данном случае, в задаче про козу.
»Люди, совершающие фундаментальные прорывы в математике, отвечают не за весь прогресс, — сказал Хоффман. – Иногда он идёт благодаря тому, что кто-то изучает классические подходы и находит в них новые методы сборки головоломки, которые в итоге могут привести к новым результатам".