Содержание
Историческая справка
Суть протокола Шнорра
Схема подписи Шнорра
Почему подписи Шнорра считаются лучше ECDSA?
Комментарий от автора
Данная статья рассчитана на людей, уже знакомых с основами защиты информации. Если слова "Протокол доказательства знания", "Криптосистема с открытым ключом" не являются для Вас заклинаниями, you're welcome!
Историческая справка
Схема Шнорра была изобретена в 1980 гг. Клаусом-Петером Шнорром. Клаус Шнорр - немецкий криптограф, академик, на тот момент профессор и исследователь Франкфуртского университета. Перед публикацией самой схемы Клаус Шнорр заморочился с патентами, из-за чего вплоть до 2008 года прямое её использование было затруднительно.
В 2008 году, в том же году, когда Сатоши Накамото представил миру Биткойн, срок действия патента Клауса Шнорра истёк. Даже несмотря на то что подписи Шнорра уже можно было использовать, Сатоши Накамото выбрал для Биткоина ECDSA. Это связано с тем, что схема Шнорра ещё не являлась стандартизированной и широко используемой.
Хоть криптографы зачастую и считают ECDSA неудачным, он до сих пор используется. К слову, DSA, предшественник ECDSA, представлял собой гибрид схем Эль-Гамаля и Шнорра, созданный исключительно для обхода патентов Клауса Шнорра Национальным институтом стандартов и технологий США (NIST). После его появления в рассылке Coderpunks начался, что называется, интеллигентный срач, а Клаус Шнорр стал ещё активнее защищать свои патенты.
Суть протокола Шнорра
Вообще говоря схема Шнорра является одним из вариантов протоколов доказательства с нулевым раскрытием. Доказываем мы то, что для некоторого публичного ключа h, который суть элемент группы с фиксированным порождающим элементом g, известен секрет x такой что g степени x суть у нас публичный ключ h.
Также, стоит заметить что протокол интерактивный, т.е. подразумевается многораундовый обмен сообщениями между участниками.
Первым делом Алиса выбирает случайное число k из подгруппы порядка q, оно должно быть уникально для каждой сессии. Затем Алиса считает I и посылает его Бобу.
Боб также выбирает случайное число из подгруппы и отправляет его обратно Алисе.
Алиса вычисляет s и отправляет его Бобу.
Боб совершает проверку и подтверждает.
Схема подписи
Эта схема является по сути развитием интерактивного протокола за исключением того, что r - не случайная величина, здесь берётся вывод случайного оракла.
Стоит заметить, что на вход хэш-функции идёт элемент группы и сообщение m (это хоть и может быть также элементом группы, но зачастую это просто битовая строка), в таком случае вместо I следует подавать выход некой функции, которая элемент группы переводит в битовую строку.
Вычисление значения r таким образом (изначальная схема подписи): называется слабым преобразованием Фиата-Шамира, оно НЕ является безопасным. На практике же стоит также добавлять в r ещё и публичный ключ pk. Слабым преобразованием Фиата-Шамира пользовались до 2010-х годов, хотя оно встречается и сейчас, в нём были найдены различные уязвимости, в частности, например, в системе электронного голосования Helios.
Тут public key (pk) - это элемент группы, т.е. его размер невелик и порядка n (на практике всего 33 байта). Отсюда следует, что размер подписи это также 2 числа из группы, т.е. 2n бит (64 байта на практике). Т.е. в сравнении с предыдущими алгоритмами этот на порядки эффективнее.
Схема подписи Шнорра позволяет подписать очень много документов (учитывая, разумеется, уникальность k). В истории были случаи, когда k совпадали в различных документах и это позволяло вскрыть ключ. Таким образом однажды уже взламывали и перепрошивали приставки, в истории Биткоина тоже были подобные случаи.
Почему подписи Шнорра считаются лучше ECDSA?
Чтобы ответить на этот вопрос давайте рассмотрим три основных критерия, по которым мы сравним ECDSA и подписи Шнорра.
Безопасность
Размер подписи
Приватность
Безопасность ECDSA
Вообще говоря, для ECDSA отсутствуют доказательства безопасности для задачи дискретного логарифмирования в группе точек эллиптической кривой при использовании случайного генератора группы, но на самом деле это не основная причина, по которой многие хотят изменить ECDSA на подписи Шнорра. С 2009 года ECDSA на кривой x3+7 достаточно надёжно работает, и если и была обнаружена какая-то критическая уязвимость, то уже давно об этом знали. То есть фактически на данный момент ECDSA и описанной кривой вполне достаточно. Выходит, дело тут немножко в другом.
Давайте рассмотрим размер подписи. Где вообще на находится это значение? У нас есть транзакция:
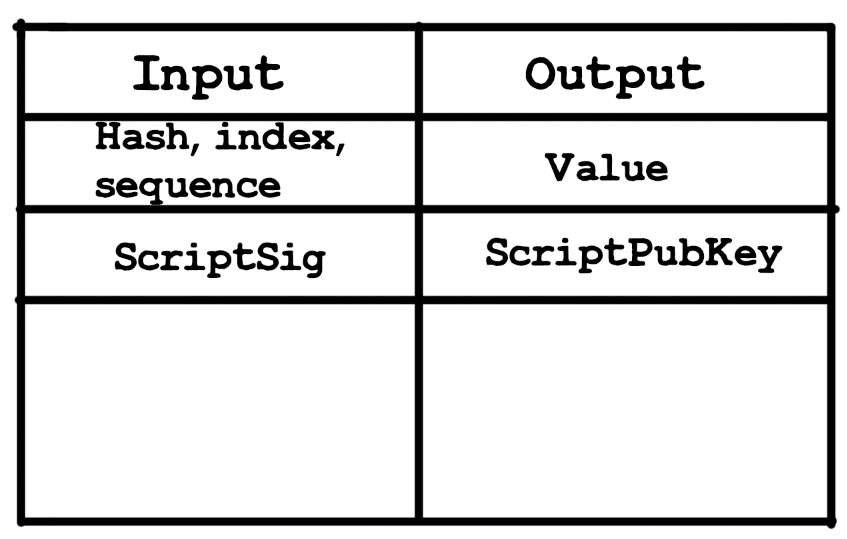
Вход транзакции состоит из хэш значения предыдущей транзакции, индекса выхода предыдущей транзакции, дальше поле sequence и собственно поле scriptSig - доказательство владения монетами, то есть собственное значение подписи, причем это значение занимает достаточно большую часть из входов транзакции.
В выходах находится value и scriptPubKey - условия траты монет, то есть по сути условия, которые должны выполняться для того, чтобы монеты были потрачены.
Если транзакцию подписывает один участник, то размер одиночного значения подписи плюс-минус одинаковый для ECDSA и для подписи Шнорра. Но что если мы используем мультиподпись, т.е. транзакцию подписывает несколько человек?
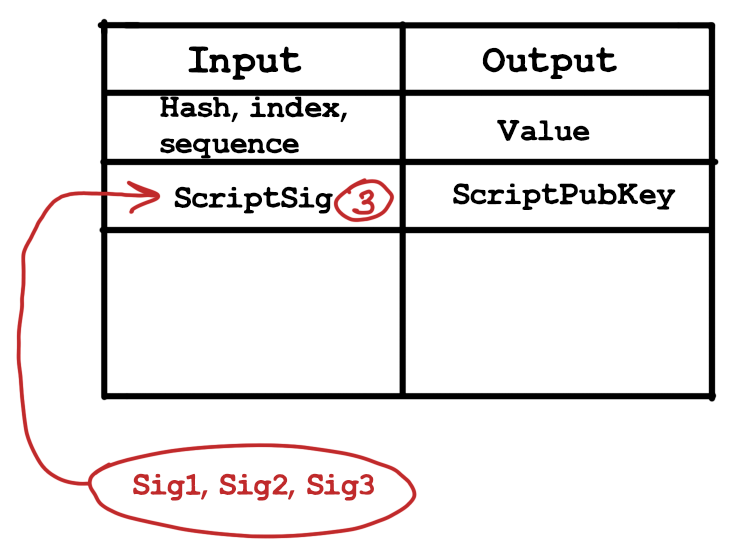
В ECDSA мультиподпись представляет из себя просто набор нескольких подписей. Так что при увеличении количества участников, которые должны подписать транзакцию, увеличивается и размер доказательства владения монетами.
Приватность ECDSA
Фактически после подтверждения транзакции каждый участник сети может точно сказать, какие ключи использовались для ее подписания. Так как мультиподпись представляет из себя набор значения подписей, каждая подпись формируется при помощи одного секретного ключа, который относится к одному публичному ключу, то есть каждый публичный ключ связан с конкретным значением подписи. Получив при верификации транзакцию с мультиподписью, можно точно сказать, какие публичные ключи были использованы, и если вы знаете, какой конкретный субъект владеет каким конкретно публичным ключом, вы можете назвать всех участников подписания той или иной транзакции. Получается, приватность не обеспечивается в принципе.

Размер подписи ECDSA
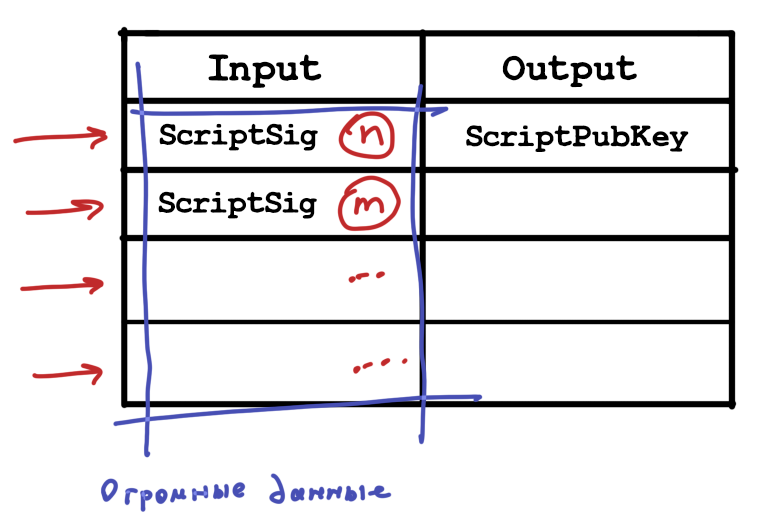
Давайте выделим ключевые поля транзакции: это scriptSig , то есть доказательства владения монетами, и scriptPubKey, то есть условия траты монет. Эти поля занимают самое большое место в входах и выходах транзакций. Изначально архитектура подразумевала, что каждый конкретный вход должен содержать значения подписи (то есть когда вы хотите потратить монет с конкретного выхода, вы должны подать на вход значение подписи). В выходе транзакций находится собственно адрес получателя. То есть как мы уже рассматривали в ECDSA, могла произойти такая ситуация, что в одном входе содержалось n значений, в другом m и т.д. Это огромные объёмы данных.
А что же подпись Шнорра?
Подпись Шнорра позволяет агрегировать значение ключей и подписи. Что такое агрегация? Пусть у нас есть 4 субъекта и есть алгоритм мультиподписи, в случае ECDSA каждый из них создает свою подпись, и на выходе получаем 4 подписи. В случае Шнорра у нас есть все те же четыре субъекта они подписывают транзакцию, значения подписи складывается и мы получаем одно общее значение, которое по размеру равно обычному значению подписи.
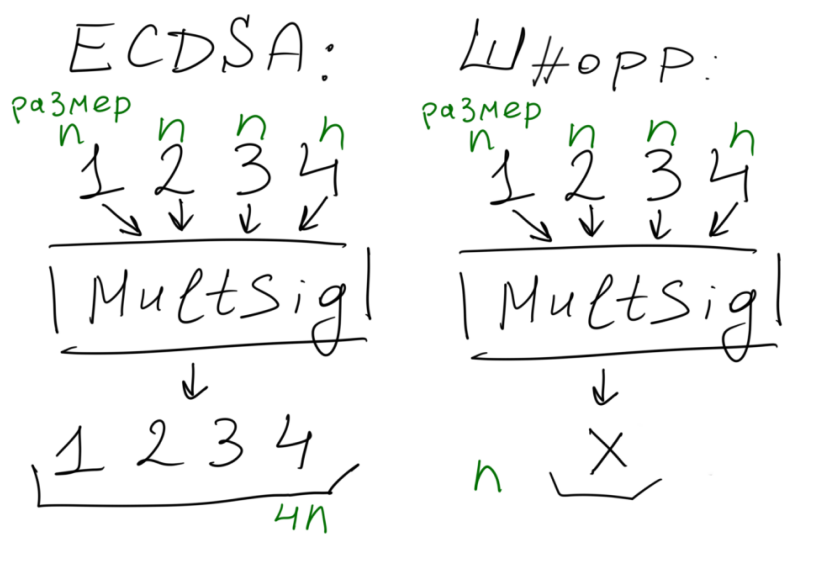
В результате, если мы применим такую вот модель для транзакции Биткойна, то каждый выход сможет иметь только одно значение подписи, это гораздо уменьшает объем доказательства владения монетами.
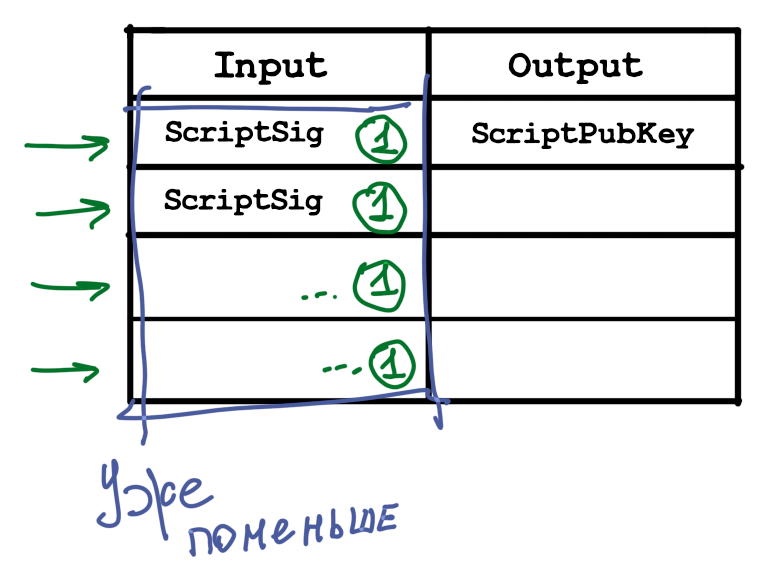
Но при этом, когда мы подписываем, определяем значение подписи для каждого входа, мы также подписываем всю транзакцию целиком. Поэтому можно провести агрегацию этих значений, то есть в итоге одно значение подписи будет покрывать всю транзакцию.

Мы агрегируем значение подписей в одно значение, и её можно будет проверить, сагрегировав наши значения публичных ключей. Мы колоссально экономим на объеме транзакции, соответственно пропускная способность повышается, так как транзакция будет занимает меньше места, а блок остается тот же самый.
Касательно приватности в подписи Шнорра. Что такое общий открытый ключ? В общем виде это сумма публичных ключей, это наш агрегированный публичный ключ. Значение подписи тоже агрегируется таким же образом, и получаем одно общее значение подписи. Этот публичный ключ соответствует этой подписи. Когда валидатор проверяет такую транзакцию, в выходе транзакции у нас находится ровно один публичный ключ, во входе транзакции находится ровно одно значение подписи. То есть независимо от того, подписал транзакцию один человек или это была мультиподпись, валидатор не замети тэтой разницы. Это положительно влияет на приватность, ведь нельзя соотнести общий открытый ключ с конкретными субъектами.
В итоге
Схема Шнорра, это одна из наиболее эффективных и теоретически обоснованных схем аутентификации. Она оказалась не очень популярна из-за продолжительного патента, продолжающегося вплоть до 2008 года. Схема хоть претерпела некоторые изменения с момента создания, но её основные идеи остались не тронутыми и высоко ценятся в криптографии.