
Доброго времени суток!
В современном мире всё больше появляется заявлений о потенциальной угрозе со стороны квантовых компьютеров по отношению к используемым протоколам криптографии. Квантовый компьютер уже способен решать задачи дискретного логарифмирования и разложения числа на множители, что ставит под угрозу все протоколы на их основе.
Сегодня рассмотрим протокол NewHope, в основе которого лежит другая сложная задача - задача обучения с ошибками в кольце (Ring-LWE).
Протокол NewHope – это протокол совместной выработки ключа, который был разработан специально, чтобы противостоять атакам с помощью квантовых компьютеров. Прежде чем переходить непосредственно к алгоритму работы, рассмотрим задачи SIS, LWE и Ring-LWE:
1. SIS как задача на решётках
SIS (Short integer solution problem) – задача поиска короткого вектора на решётке в окрестности точки.
Имеется матрица А, столбцы которой состоят из целочисленных векторов длины n по модулю q (вектора выбираются случайно):
Также введем символ или же ортогональную решётку от A:

На рисунке показана решётка с некоторым базисом (не обязательно кратчайшим) и выделенный квадрат, который и ограничивает по модулю значения точек решётки.
Задача состоит в том, чтобы при заданной матрице А найти ненулевой вектор решётке такой, что
. Задача решается методом Гаусса и, отчасти, ничего сложного в ней нет.
Введем параметр и поставим условие, что мы ищем достаточно короткий вектор z, такой что
. Это условие должно выполняться для любого положительного вектора z (они целочисленные по модулю q). Аналогично задачу можно перефразировать так, что мы ищем вектор, принадлежащий окрестности точки решётки. Так как мы матрицу А выбирали случайным образом, то мы поставили задачу в общем случае.
Как можно усложнить задачу? Сдвинем решётку на небольшое расстояние, это привнесет в нее шум (главное не сдвигать слишком сильно).
Предлагается выбирать сдвиг - периода решётки. Иначе возникнет проблема с восстановлением вектора z.
Теперь после внесения шума, искать короткий вектор z по заданному A становится очень сложной задачей.
Если мы работаем в евклидовой норме, то можем получить асимптотическую сложность в , где n - размерность пространства.
2. LWE ( Learning with errors)
Рассмотрим задачу обучения с ошибками:
Параметры задачи:
n – размерность пространства;
q – число, как и в прошлой задаче. Здесь оно берется с полиномиальной зависимостью от n, порядка ;
А также функция распределения ошибок берется нормальное распределение, для красивых формул в доказательствах);
Как и в прошлой задаче зададим случайную матрицу столбцы которой вектора
;
И вектор k, который будет отвечать за шум из распределения .
Задача состоит в том, что злоумышленнику необходимо найти секретный вектор , когда ему известны всевозможные зашумленные скалярные произведения s с векторами
. (Все операции выполняются по модулю q):
Или точнее
Где первая компонента вектора
.
Однако нас интересует модификация задачи, так называемое обучение с ошибками на решётках (LWE on lattices).
Зададим решётку:

Задача уже подменяется другой – декодирование с ограниченным расстоянием.
Задана решётка, и дана точка q. Необходимо в её окрестности найти ближайшую к ней точку решётки.
Так же, как и в прошлых задачах вносим шум в решётку, тогда задача нахождения ближайшего вектора становится очень сложной:
Дано: найти
.
3. Примеры
Рассмотрим создание криптографической системы с открытым ключом на LWE, а также хеш-функцию на SIS:
Public key encryption (LWE):
Боб хочет отправить сообщение Алисе, зашифрованное с помощью её открытого ключа. Сообщение в данном примере – бит информации.

В данной схеме надо учесть, что разность ошибок
Если получившаяся разность ближе к 0, то декодирован 0, и если к то 1.
Что у нас знает хакер? и
. Так как в них замешано умножение на случайную матрицу
с примесью шума, то выходит, что на руках у него 4 случайных величины, с помощью которых узнать сообщение не выйдет.
One-way function (SIS):
Построение хеш-функции предлагается осуществлять по схеме Меркла-Дамгора:

Происходит разбиение изначального сообщения произвольной длины на блоки одинаковой длины, а в дальнейшем потоковая обработка с помощью функции сжатия. В каждой итерации конвейера принимается входной блок и блок от предыдущего сообщения. В начале все инициализируется вектором инициализации (IV).
Дамгор и Меркл независимо показали, что если будет устойчивой к коллизиям, то и
будет устойчива.
Наша задача построить функцию - устойчивую к коллизиям (One-way function):
Так же, как и ранее определим:
зафиксируем
и
.
Определим - семейство функций
такие что
И для битового вектора функция будет задаваться как:
Определение довольно естественное в контексте задачи SIS.
Что насчет коллизий? Была доказана лемма, что сложность нахождения коллизии в указанной выше задачи с вероятностью аналогична сложности решения задачи SIS с той же вероятностью.
4. Проблемы с использованием этих задач в реальных криптосистемах
При использовании в реальных криптосистемах возникает ряд проблем:
Необходимость пересылки очень большого количества данных. На слайде приведена матрица для размерности
и ограничением 15 бит на число:

2) Все операции шифрования/дешифрования происходят с асимптотической сложностью , что довольно медленно.
Какое решение у этих проблем?
5. Ring-LWE
Обучение с ошибками в кольце решает сразу обе вышеописанные проблемы.
Какая идея была у создателей? Вспомним, что в LWE задаче мы имеем много разных скалярных произведений. Что если задать операцию скалярного произведения так, чтобы мы могли получить n псевдослучайных скаляров из одного?
Как определить операцию ?
Наилучший способ – умножение в кольце многочленов , где
, n – степень двойки.
Элементы имеют степень
c коэффициентами по модулю q.
Почему именно такой способ? Необходимость передавать большие матрицы отпадает. В самом деле, достаточно передать один полином, остальные можно получить циклическим сдвигом по правилу: . В итоге получаем достаточно случайную матрицу.
Что насчет шифрования/дешифрования? С помощью быстрого преобразования Фурье, можно получить перемножение 2 полиномов за , что значительно быстрее
Задача получается аналогичной LWE за исключением того, что уже являются полиномами, а не просто векторами.
6. Протокол NewHope
Если кратко говорить, то протокол NewHope является модификацией протокола обмена ключами, который описали в своей статье Bos, Castello, Naehrig и Stebila. Они реализовали обмен ключами в TLS из Ring-LWE.
Я не буду приводить детального сравнения изменений между этими протоколами, а опишу общий алгоритм работы и мотивацию в выборе тех или иных параметров в протоколе NewHope.
В данной схеме я буду пользоваться обозначениями, введёнными авторами статьи.

Разберём стадии и функции подробнее:
Здесь Алиса является сервером, а Боб клиентом.
В качестве параметров системы n = 1024, q = 12289 (наименьшее простое, для которого
). Это необходимо для быстрой работы NTT (вариация дискретного преобразования Фурье для полиномов), который требует n – степени двойки, q – простое число, которое соответствует указанному выше требованию. Используется решётка
В начале необходимо сгенерировать случайный полином a. Происходит это так: генерируется seed – псевдослучайное число длиной 256 бит, далее это число пропускается через функцию SHAKE-128 (в работе авторов в качестве данной функции используется SHA3). Затем начинает работать парсер, который выберет 1024 коэффициента в полином a. Небольшая ремарка: несмотря на то, что TLS имеет кэширование ключей на некоторое время (в районе 2 часов), авторы протокола NewHope выступили против этого, и по умолчанию для каждого нового соединения генерируется свой полином a. По их мнению, это уменьшает шанс на backdoor и возникновения проблемы, что все соединения будут полагаться на единственный “экземпляр” задачи в решётках.
Функция распределение ошибок – биноминальное, центрированное. Это сделано из-за того, что моделировать нормальное распределение довольно затратно и не нужно хранить таблицы вычисленных значений (что исключает некоторые типы атак). Здесь использован псевдослучайный генератор с seed из /dev/urandom с последующим быстрым суммированием 16-битовых блоков вывода. Выборкой из нее получаем коэффициенты для секретного полинома s и полинома ошибок e.
Пересылается пара (открытый ключ b, seed).
На стороне клиента также генерируется полином a, полиномы s’, e’, e”, вычисляется открытый ключ u.
Дальше необходимо получить полином v, который должен быть одинаковым и для клиента, и для сервера. Однако с этим возникают трудности. На стороне клиента получается
, на стороне сервера
, в итоге накапливается погрешность между полиномами, которую необходимо исправить. Если помните, различение переданного бита – это то, насколько значение близко к 0 или
. Соответственно, большая погрешность может привести к искажению сообщения.
Выполним коррекцию ошибки. Для начала вернемся от полиномов к векторам: коэффициенты полинома будут координатами вектора. Разделим их на q и таким образом, отобразим их на
. Так как мы работаем в решётке
то для примеров перейдем в
(в четырёхмерном пространстве рисовать тяжело). Для начала немного изменим нашу решетку и перейдем к базису
. На двумерной решётке нужно нарисовать диаграмму Вороного.
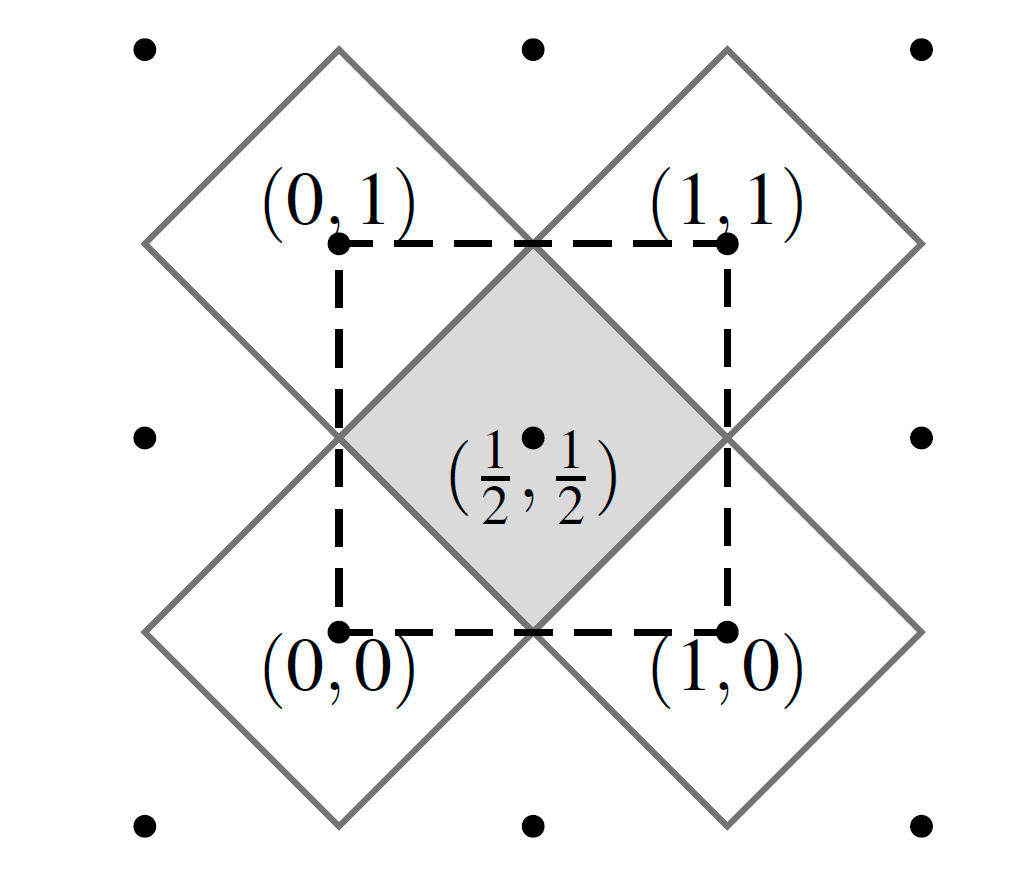
И наша задача отобразить вектор в бит информации однозначно. Допустим, что клиент и сервер имеют один и тот же вектор, тогда отображение вектора в бит информации довольно простое: если вектор попал в серую область ячейки Вороного, то он 1, если вне её, то 0. Однако все усложняется тем, что у клиента и сервера есть только зашумленные варианты векторов, так что можно получить разные значения. Для исправления этого вводится функция HelpRec, которая находит сдвиг до ближайшей точки решётки. Её необходимо выполнить на одной из сторон и результат переслать второй стороне. Важно то, что она сообщает сдвиг до ближайшей точки решётки, а не какой бит должен получиться.
8. Далее функция Rec ищет 1 бит ключа из 4 коэффициентов полинома (с учетом сдвига).
9. После хеширования получаем ключ длиной 256 бит, который будет одинаковым и у клиента, и у сервера.
7. Применение и стандартизация
Протокол был предложен в 2019 NIST post-quantum crypto project, прошел во второй раунд, но не прошел в третий раунд. В отчете NIST говорится, что благодаря своей структуре протокол имеет очень высокую производительность, однако он не превзошел своего конкурента KYBER (который основан на задаче Module-LWE) по безопасности, а также проиграл ему в ряде бенчмарков. В итоге в 3 раунд прошел протокол KYBER.
Также, протокол тестировал Google в проекте Canary вместе со своим CECPQ1 и CECPQ2.
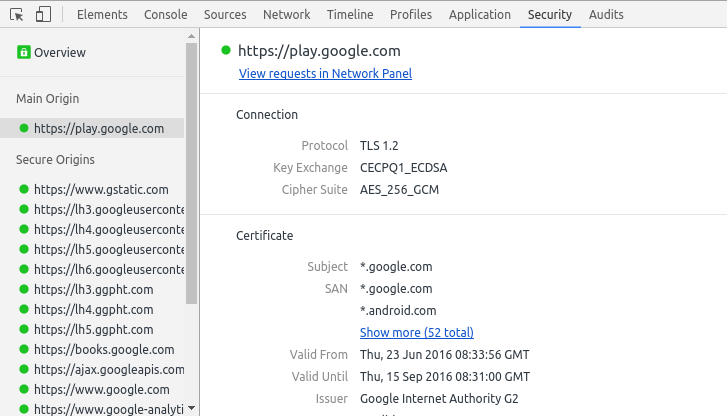
Реализации протокола:
Источники:
https://www.di.ens.fr/chloe.hebant/presentation/SISproblem.pdf
http://www.ee.cityu.edu.hk/~twhk05/achieve/Wai%20Ho%20Mow.pdf
https://simons.berkeley.edu/talks/lwe-worst-case-average-case-reductions-and-cryptomania
https://simons.berkeley.edu/talks/algebraic-lattices-and-ring-lwehttps://www.ei.ruhr-uni-bochum.de/media/sh/veroeffentlichungen/2013/08/14/lwe_encrypt.pdf
https://security.googleblog.com/2016/07/experimenting-with-post-quantum.html