4uvak Jun 9 2020 at 13:58

Оценка рыночного риска (Value at Risk) портфеля облигаций (теория)

15 min

15K

Достаточно много работ написано на тему вычисления такого показателя, как $inline$ (Value at Risk), в том числе и различные статьи в интернете. Однако, честно признаться, действительно качественных из них оказалось мало. Да и работ, посвященных оценке $inline$ инструментов, отличных от акций, тоже немного. Те, кто хочет разобраться с тем, что же это такое и какая математическая модель стоит за вычислением $inline$ портфеля облигаций, прошу под кат.

Введение

На практике в качестве основной метрики, способной производить расчет и сравнение рисков по различным финансовым вложениям является мера $inline$ (Value at Risk). В RiskMetricks, составленной банком J.P.Morgan в 1996 году, именно эта мера является основной для оценки рыночных рисков. С тех пор многие банки и финансовые организации начали следовать данному техническому документу для оценки рисков собственных вложений, и данная величина неформально стала главной мерой рыночного риска.

Подойдем к определению данной величины издалека.

Параметрический метод расчёта VaR

Рассмотрим абстрактную случайную величину $inline$ . В самом общем случае квантилем уровня $\alpha \in [0,1]$ случайной величины $inline$ называется такое число $q_\alpha$ , которое удовлетворяет следующей системе:

$\begin{cases} P(X < q_\alpha) \leq \alpha \\ P(X \leq q_\alpha) \geq \alpha \end{cases}$

Рассмотрим те случайные величины, у которых функция распределения непрерывная и строго возрастающая. Тогда определение квантиля случайной величины можно упростить и записать в следующем виде:

$P(X < q_\alpha) = \alpha$

а значение $q_\alpha$ в таком случае будет определяться однозначно.

Замечание

Если не вводить предположение о непрерывности и возрастании функции распределения, то значение $q_\alpha$ определяется не однозначно и, вообще говоря, может принимать любое значение из допустимого отрезка. Для преодоления этой неоднозначности можно, например, брать середину этого отрезка

Именно понятие квантиля случайной величины является основой для определения $inline$ (Value-at-Risk) ценной бумаги или целого портфеля бумаг. С математической точки зрения, при заданном уровне значимости $\alpha$ (доверительный уровень), $inline$ определяется как квантиль некоторой случайной величины $R_t^{(n)}$ :

$P(R_t^{(n)} < VaR) = \alpha$

В этом примере $R_t^{(n)}$ является доходностью ценной бумаги или портфеля бумаг на момент времени $inline$ за период $inline$ , которая рассматривается как случайная величина.

Таким образом, величина $inline$ имеет следующий вполне явный смысл, который зачастую берется как некоторое классическое определение: $inline$ — это величина убытков, которая с вероятностью, равной уровню доверия $\alpha$ , не будет превышена в течение $inline$ дней.

Замечание

Стоит заметить, что в жизни принято измерять $inline$ в деньгах, а в данном случае величина $R_t^{(n)}$ – это доходность, которая измеряется в долях (или процентах). Такое представление не случайно. Дело в том, что перейти от доходности к деньгам (денежному выражению величины) не составит никакого труда. Для этого достаточно будет знать предыдущую рыночную стоимость ценной бумаги или рыночную стоимость портфеля бумаг, тем самым после преобразования получив нужную ожидаемую величину убытков. Но в дальнейшем такое определение немного упростит все выкладки, которые необходимо будет проводить при расчёте $inline$ портфеля ценных бумаг

Существует несколько способов или методов оценки нужного нам квантиля случайной величины. Самые известные из них

исторический метод
параметрический метод

Первый способ – это оценка по историческим данным, когда распределение доходностей берется из уже реализовавшегося временного ряда, то есть неявно предполагается, что доходности в будущем будут вести себя похожим на то, что уже наблюдалось, образом. В таком случае функция распределения строится по историческим данным (она будет ступенчатой и разрывной) и на ее основе вычисляется необходимый $inline$
Второй способ – это параметрический подход, когда расчёты проводятся в предположении, что известен вид распределения доходностей. Естественно, параметры предполагаемого распределения оцениваются по историческим данным (например, методом максимального правдоподобия или методом моментов), однако сам квантиль, в отличие от исторического метода, уже ищется строго из аналитических соотношений.

Здесь же следует отметить еще один способ, который любят выделять в отдельную категорию: это оценка $inline$ методом Монте-Карло. Он достаточно схож с параметрическим методом, однако есть существенное отличие. Зачастую распределение доходностей берется не из какого-либо заранее известного и хорошо изученного параметрического класса распределений, а оценивается по историческим данным (например, методами ядерного сглаживания). Далее генерируется огромное число выборок (бутстрэп) большого объема из оцененного распределения и по каждой из них оценивается необходимый квантиль, то есть величина $inline$ . Итоговый результат усредняется по всем выборкам. Данный подход можно назвать некоторым улучшением исторического метода.

Мы рассмотрим только параметрический подход к оценке $inline$ . Более того, рассмотрим лишь случай, когда распределение доходностей является нормальным. Часто приводят следующие аргументы против использования предположения о нормальном распределении доходностей:

эмпирическое распределение доходностей финансовых активов обычно имеет более «тяжелые хвосты», чем это свойственно нормальному распределению;
распределение доходностей финансовых активов обычно не абсолютно симметрично.

«Тяжелые хвосты» является, пожалуй, наиболее серьезной проблемой среди перечисленных выше. Данное явление свидетельствует о более частом возникновении крупных потерь или доходов, чем это характерно для нормального распределения. Таким образом, вероятность превышения расчетного показателя $inline$ для заданной доверительной вероятности $\alpha$ , на самом деле выше, чем $(1-\alpha)$ . На практике эта проблема может быть частично решена за счет применения мультипликатора экономического капитала (это некоторый множитель или слагаемое для увеличения полученного расчетного значения), созданного для защиты от непредвиденных потерь.

Однако, когда собирается портфель ценных бумаг, то доходность такого портфеля все-таки можно в какой-то степени считать нормальной случайной величиной, особенно если бумаг в портфеле много и они достаточно ликвидны, потому что в таком случае применима центральная предельная теорема. И даже если доходность портфеля не подчиняется нормальному распределению, то тем не менее результаты получаются вполне приемлемыми для практики.

Итак, предположив некоторое распределение для доходности актива (в нашем случае мы делаем предположение о нормальном распределении), можно в явном виде выразить значение величины $inline$ :

$P\left(\frac{R_t^{(n)}-\mu^{(n)}}{\sigma^{(n)}} < \frac{VaR-\mu^{(n)}}{\sigma^{(n)}}\right) = \alpha$

$VaR=\mu^{(n)}+\sigma^{(n)}\Phi^{-1}(\alpha)$

где $\Phi^{-1}(\alpha)$ – квантиль уровня $\alpha$ стандартной нормальной случайной величины, а $\mu^{(n)}$ , $\sigma^{(n)}$ – математическое ожидание и стандартное отклонение случайной величины $R_t^{(n)}$ , то есть доходности.

Горизонт прогнозирования

Следует помнить, что при расчете $inline$ предполагается, что убыток будет получен на некотором горизонте $inline$ , который возможно получить с заданной вероятностью. Однако на практике неудобно вычислять каждый раз $inline$ на разные сроки, поэтому принято вычислять его немного по-другому. Так как для оценки квантиля так или иначе нужно использовать исторические данные, то неявно предполагается, что реализовавшиеся доходности были получены из одного распределения, так же, как и будущие доходности будут подчиняться этому распределению.

Более формально, имеем ряд $\cdots,R_{t-2}^{(n)},R_{t-1}^{(n)},R_t^{(n)},R_{t+1}^{(n)},R_{t+2}^{(n)},\cdots \sim iid R^{(n)}$ . Это значит, что имеется стационарный случайный процесс $\{R_t^{(n)}, t \in \mathbf{Z}\}$ (или $\{R_t^{(n)}, t \in \mathbf{N}\}$ ), если мы условимся о моменте начала этого процесса) – последовательность независимых случайных величин с одинаковым распределением. Во-первых, это дает полное право считать, что $R_t^{(n)} \equiv R^{(n)} \forall t$ и числовые характеристики случайного процесса не зависят от времени. Во-вторых, этот стационарный случайный процесс есть не что иное, как стационарная цепь Маркова, которая является частным случаем эргодической цепи Маркова. Для таких цепей справедлива следующая теорема:

Эргодическая теорема
Усреднение по статистическому ансамблю равносильно усреднению по времени.

Это означает, что для эргодических систем математическое ожидание по временным рядам должно совпадать с математическим ожиданием по пространственным рядам. Тогда пронаблюдав за доходностями во времени, можно оценить статистические показатели случайной величины $R^{(n)}$ .

Более того, приняв за $R^{(n)}$ логарифмическую доходность, можно выразить доходность за промежуток $inline$ через однодневную доходность. Имеем

$R^{(n)} = R_t^{(n)} = \ln \frac{P_{t+n}}{P_t} = \ln \prod_{i=0}^{n-1}{\frac{P_{t+i+1}}{P_{t+i}}} = \sum_{i=0}^{n-1}\ln \frac{P_{t+i+1}}{P_{t+i}} = \sum_{i=0}^{n-1}{R_{t+i}^{(1)}} = \sum_{i=0}^{n-1}{R^{(1)}} = \sum_{i=1}^n{R}$

$\mu^{(n)} = E(R^{(n)}) = E\left(\sum_{i=1}^n{R}\right) = n\mu$

$\sigma^{(n)} = \sqrt{D(R^{(n)})} = \sqrt{D\left(\sum_{i=1}^n{R}\right)} = \sqrt{\sum_{i=1}^n{D(R)}}=\sqrt{n}\sigma$

Тогда окончательно формула $inline$ имеет вид:

$VaR = n\mu + \sqrt{n}\sigma \Phi^{-1}(\alpha)$

Именно эту формулу можно увидеть во всевозможных источниках о вычислении $inline$ и выводится она при достаточно жестких предположениях, которые почти никогда не выполняются на практике. Тем не менее он очень красив и приводит к достаточно приемлимым результатам. Более того, если считать, что $\mu \approx 0$ , а это действительно правдоподобное предположение, которое часто подтверждается на практике, вычисление $inline$ становится особенно простым. В историческом методе поступают так же: вычисляют однодневный $inline$ , а потом, используют данное соотношение, рассчитывают $inline$ -дневный $inline$ . В дальнейшем все вычисления сделаны для однодневного $inline$ , помня при этом, что перейти к $inline$ -дневному $inline$ можно просто домножив соответствующие слагаемые на нужный коэффициент.

Расчет VaR для акций

Рассмотрим одну единственную акцию. Пусть мы пронаблюдали за ценой данной акции в течение $inline$ дней, то есть имеем некоторый ценовой ряд $(p_0,p_1,p_2,\cdots,p_n)$ (здесь и далее $inline$ — это не период, на который мы хотим прогнозировать $inline$ из предыдущего параграфа, это количество дней, в течении которых мы наблюдали за данными). Перейдем от цен к доходностям по следующей формуле:

$r_t = \frac{p_t-p_{t-1}}{p_{t-1}} \approx \ln \frac{p_t}{p_{t-1}}$

то есть получим ряд доходностей $(r_1,r_2,\cdots,r_n)$ . Далее оценим по полученным историческим данным математическое ожидание и стандартное отклонение случайной величины $inline$ :

$\mu = E(R) = \frac{1}{n} \sum_{t=1}^n{r_t}$

$\sigma^2 = D(R) = \frac{1}{n-1} \sum_{t=1}^n{(r_t-\mu)^2}$

На данном этапе все необходимые величины известны и можно с легкостью найти требуемую величину $inline$ .
В случае портфеля бумаг из акций требуется так же учесть и взаимосвязь доходностей различных акций между собой. Пусть имеется $inline$ акций в портфеле. Доходность $inline$ -ой акции обозначим за $inline$ (случайная величина). Вес $inline$ -ой акции обозначим за $inline$ , $\sum_{i=1}^k{w_i}=1$ . Иными словами, имеется вектор доходностей $\boldsymbol{R}=(R_1,R_2,\cdots,R_k)^T$ (случайный вектор) и вектор весов $\boldsymbol{w}=(w_1,w_2,\cdots,w_k)^T$ . Тогда формулы для матожидания и стандартного отклонения доходности портфеля будут выглядеть следующим образом:

$\mu = E(R) = \boldsymbol{w}^T E(\boldsymbol{R})=\boldsymbol{w}^T \boldsymbol{\mu}$

$\sigma^2 = D(R) = \boldsymbol{w}^T\boldsymbol{C}\boldsymbol{w}$

где $\boldsymbol{\mu} = (\mu_1,\mu_2,\cdots,\mu_k ) = E(\boldsymbol{R}) = (E(R_1),E(R_2),\cdots,E(R_k))$ – вектор матожиданий, а

$\boldsymbol{C} = \begin{pmatrix} Cov(R_1,R_1) & Cov(R_1,R_2) & \cdots & Cov(R_1,R_k) \\ Cov(R_2,R_1) & Cov(R_2,R_2) & \cdots & Cov(R_2,R_k) \\ \cdots & \cdots & \cdots & \cdots \\ Cov(R_k,R_1) & Cov(R_k,R_2) & \cdots & Cov(R_k,R_k) \end{pmatrix}$

– ковариационная матрица доходностей. Вычислив данные величины, можно найти $inline$ портфеля, состоящего из акций. Стоит заметить, что даже если в портфеле много бумаг (а на практике это около 10-30 штук), нахождение данных значений не является вычислительно сложной задачей.

Отличие облигаций от акций

В отличии от акций, время жизни облигаций – заранее известная характеристика и чем ближе дата экспирации, тем меньше колебания цены. К тому же, при первичном размещении часто бывает так, что весь выпуск данной серии облигаций распределяется между не очень большим числом институциональных инвесторов, которые не всегда торопятся расторговывать данный выпуск (только если это не маркет-мейкеры). Ведь в ходе аукциона каждый из инвесторов получил пул облигаций по той цене, которая приносит комфортную ему доходность, и пока конъюнктура рынка не изменится, хочется держать эту серию до погашения, а не продавать ее в рынок. Бывает конечно, что ситуация складывается наоборот, и в ходе аукциона получилось купить облигацию с дисконтом к рынку (например, если это было доразмещение), что наоборот влечет мгновенные продажи инструмента в рынок. Однако в любом случае у облигаций, зачастую, маленькая волатильность в начале и в конце обращения, а в середине своего времени жизни облигации обычно имеют наибольшую волатильность.

Реальный пример из рынка представлен на рисунке ниже. Это погашенная в мае 2020 года ОФЗ 26214. Ее однодневная доходность, если считать доходность по цене, убывает по мере наступления даты экспирации.

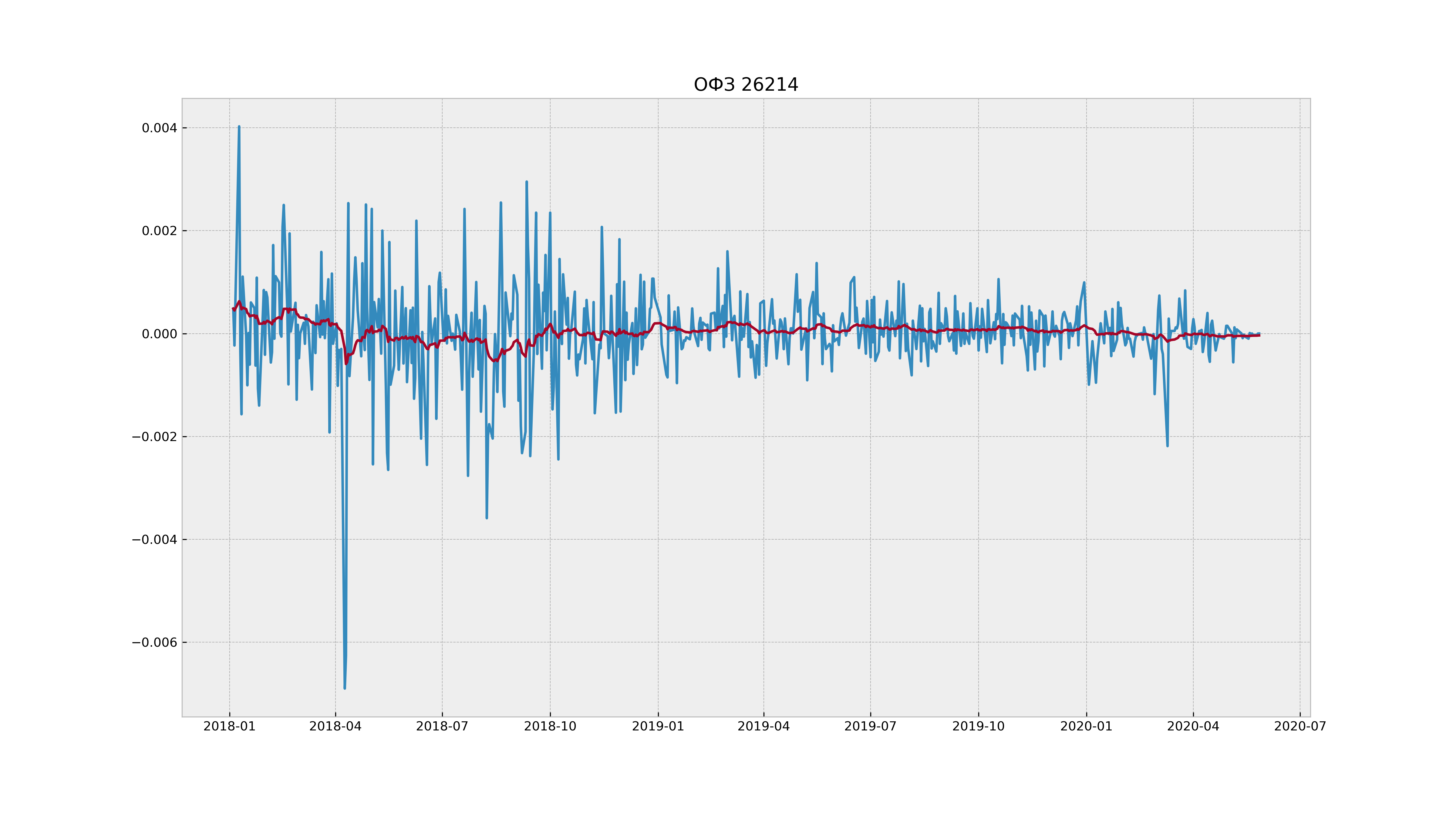
Далее представлено как менялась волатильность (в данном случае дисперсия) доходности, рассчитанной по цене. Видно, что по мере приближения даты погашения волатильность убывает

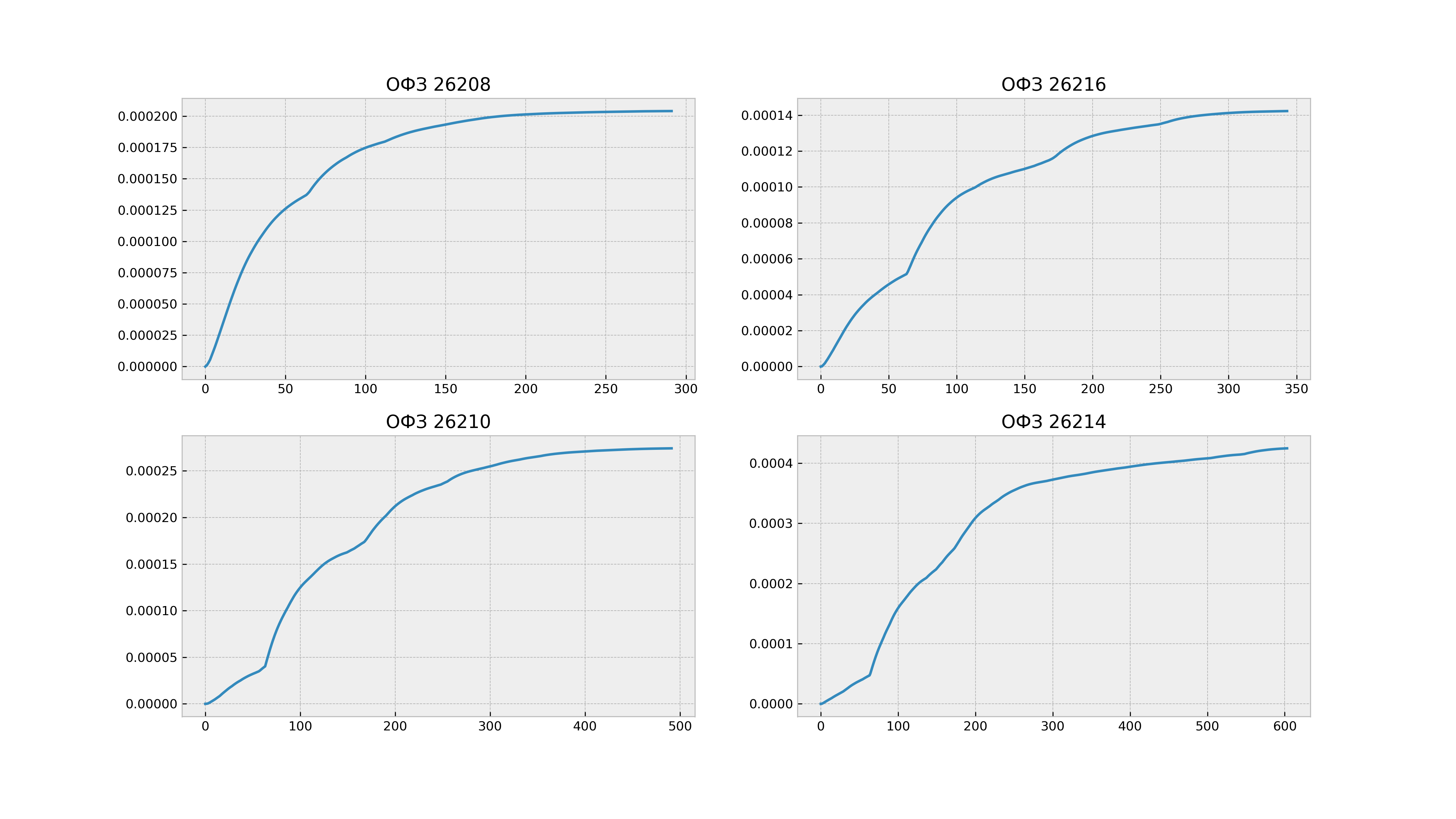
И, наконец, далее представлена волатильность (дисперсия) на период $inline$ , где хорошо видно, что дисперсия не растет линейно от $inline$ .

Еще примеры

Для сравнения приведем оценки доходностей по цене у акций компании «Яндекс», а также их волатильность

Еще примеры

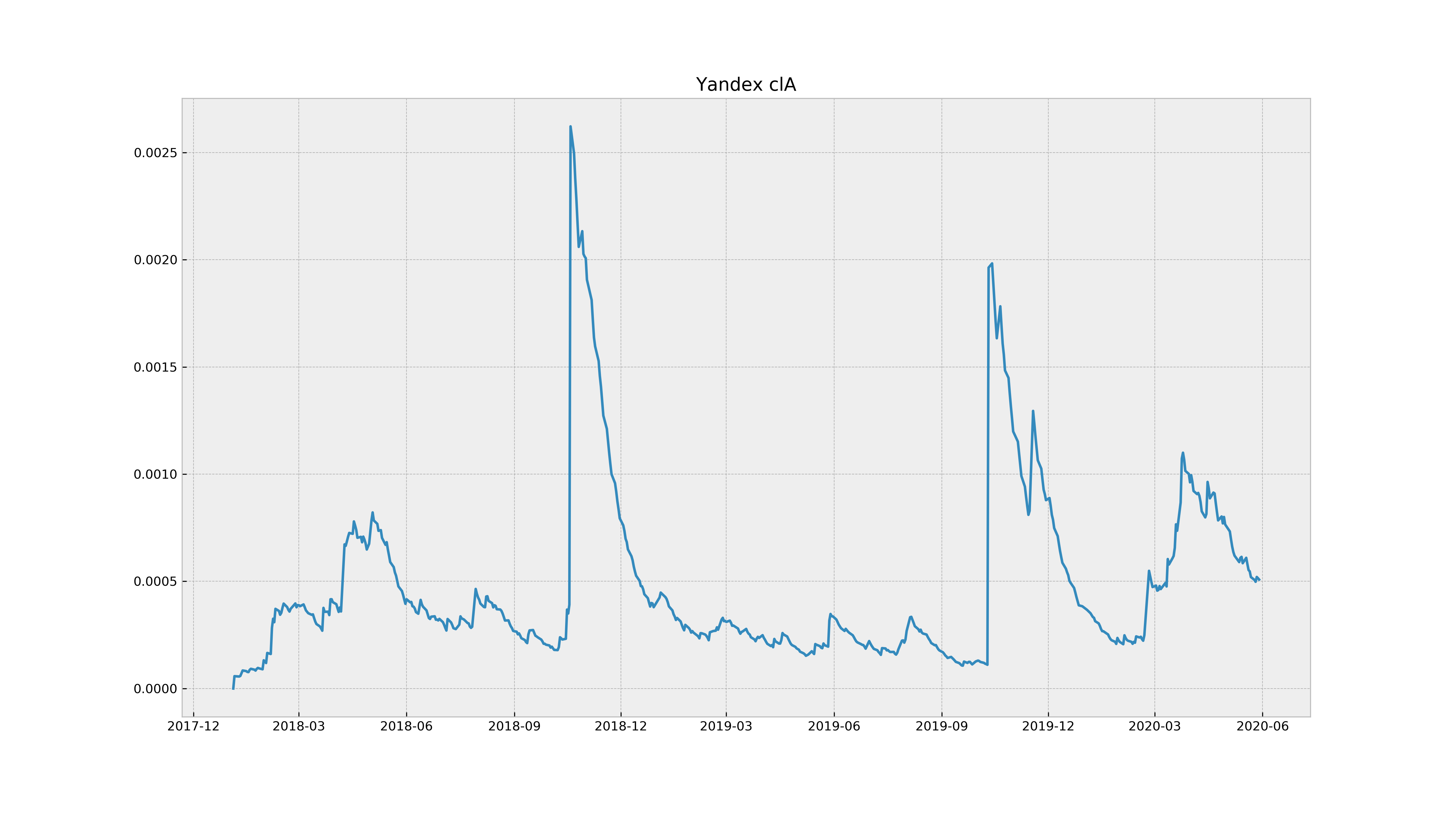
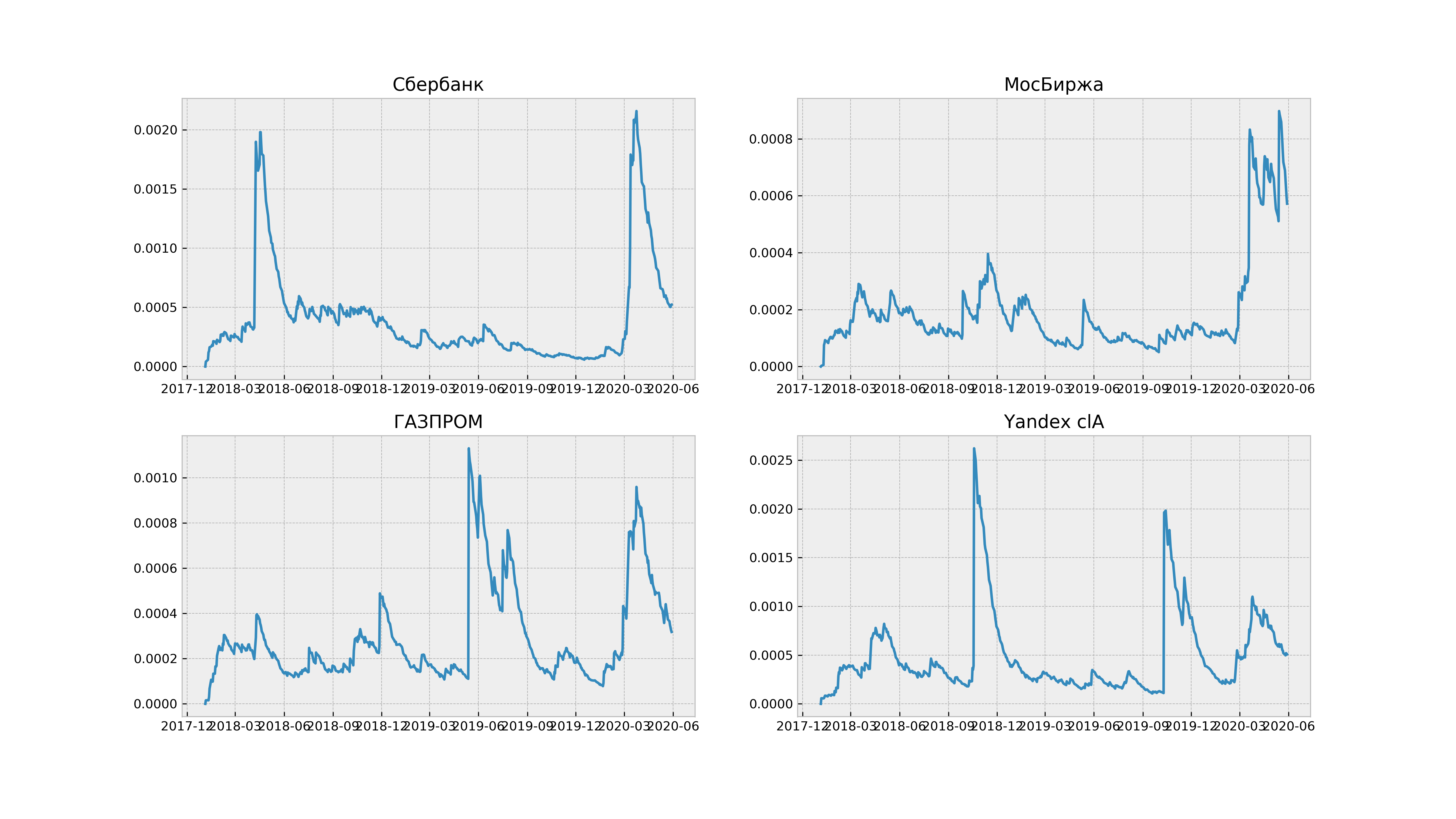
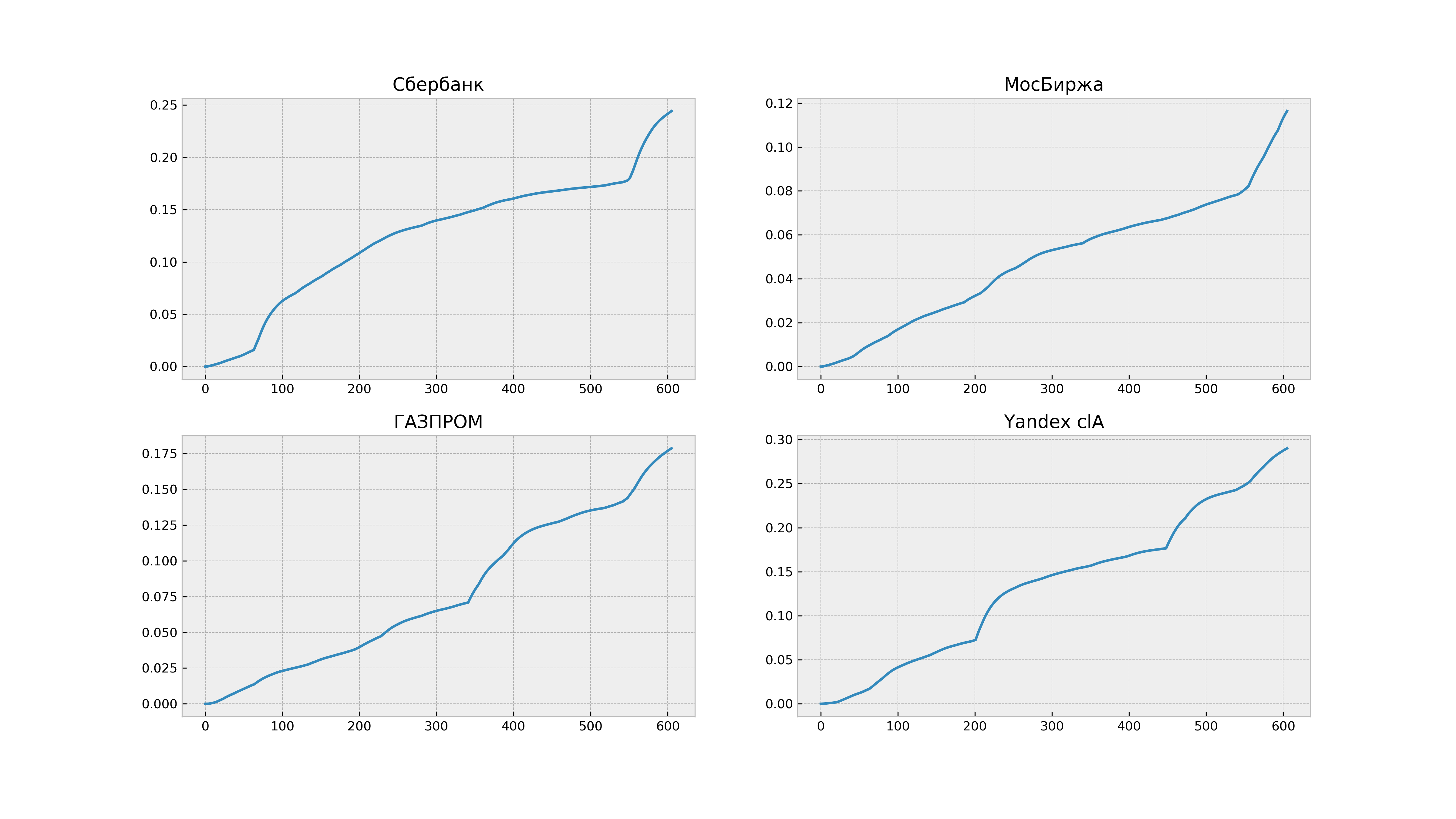
В случае акций доходность ведет себя ближе к стационарному процессу, а дисперсия с увеличением $inline$ растет практически линейно, что как раз и позволяет считать цену акций хоть в какой-то степени за винеровский процесс.

Для облигаций некорректно переходить от цен к доходностям и оценивать параметры распределения по полученным историческим данным, потому что доходности в таком случае не будут являться стационарным случайным процессом (однако в принципе так можно делать, если облигация достаточно длинная и рассматривается на периоде, много меньшем, чем время жизни облигации). В данном случае следует использовать другой подход.

Расчет VaR для бескупонной облигации

Для начала рассмотрим самый простой случай – единственную бескупонную облигацию. Пусть наша бескупонная облигация имеет номинал $inline$ , а дата ее погашения – $inline$ . Тогда справедливая стоимость данной облигации в момент времени $inline$ :

$p_t=C \exp(-y_{t,(T-t)}(T-t))$

где $inline$ – время до погашения облигации в годах, $y_{t,(T-t)}$ – безрисковая ставка на рынке на момент времени $inline$ сроком на $inline$ лет. Тогда доходность данной облигации можно выразить следующим образом:

$r_t = \ln \left( \frac{p_t}{p_{t-1}}\right) = -[y_{t,(T-t)}(T-t) - y_{t-1,(T-t+\boldsymbol{1})}(T-t+\boldsymbol{1})] = -d \Delta y_{t,(T-t)}$

где $\boldsymbol{1}$ – один день, $T-t+\boldsymbol{1}\approx T-t = d$ – время до погашения (считаем, что $T-t \gg \boldsymbol{1}$ ) и в случае бескупонной облигации это время равно дюрации данной облигации.

В терминах случайных величин запишем данное соотношение следующим образом:

$R = -dY_{T-t}$

где случайная величина $Y_{T-t}$ обозначает абсолютное изменение ставки сроком на $inline$ лет, $inline$ – дюрация бескупонной облигации.

Именно изменение ставки $Y_{T-t}$ следует считать первостепенной величиной, влияющей на доходность облигации, тогда как к самой доходности мы переходим через коэффициент $inline$ .
Действительно, посмотрим на поведение абсолютного изменения ставки на срок в полгода на примере реальных данных:

Еще примеры

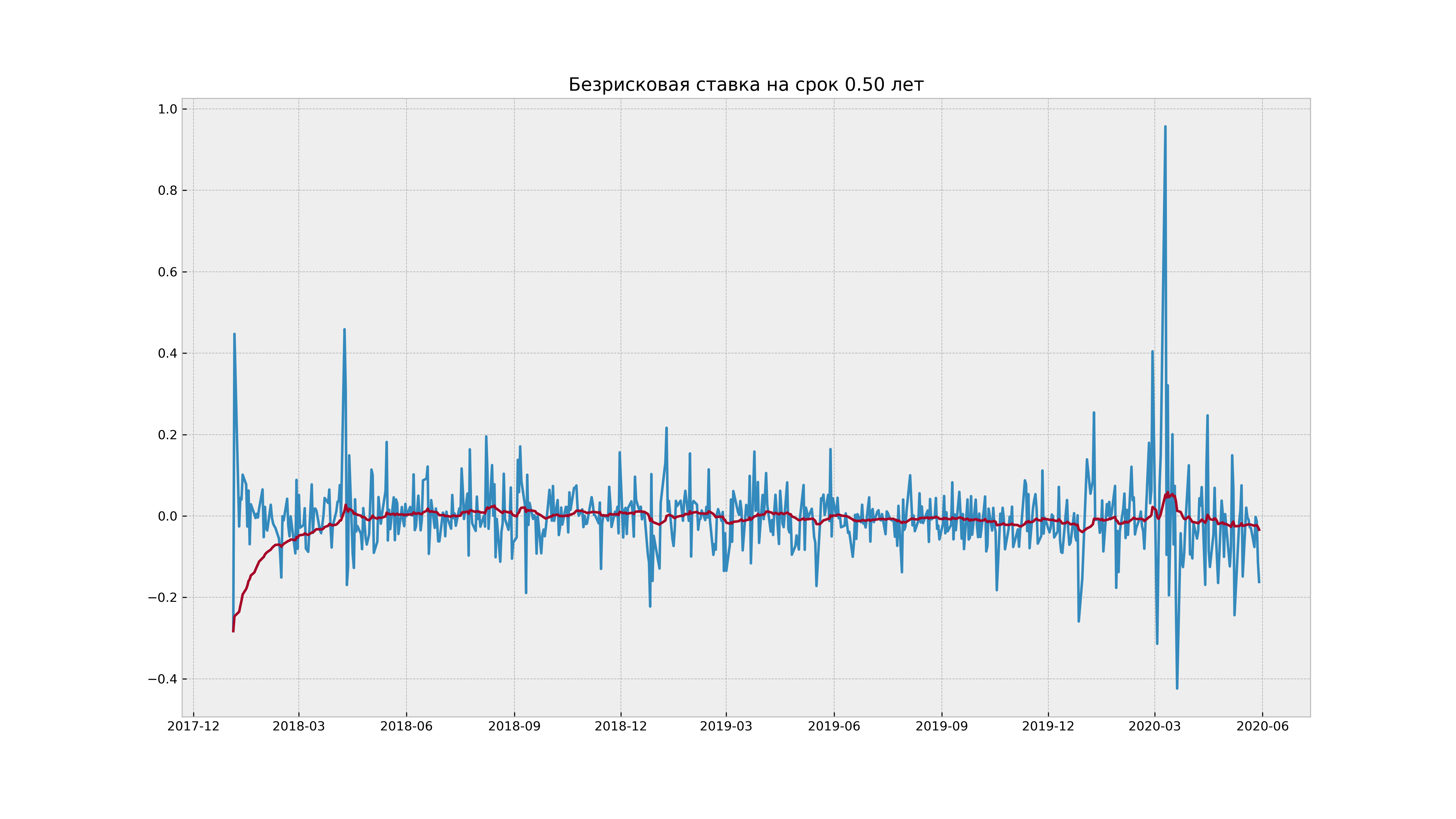
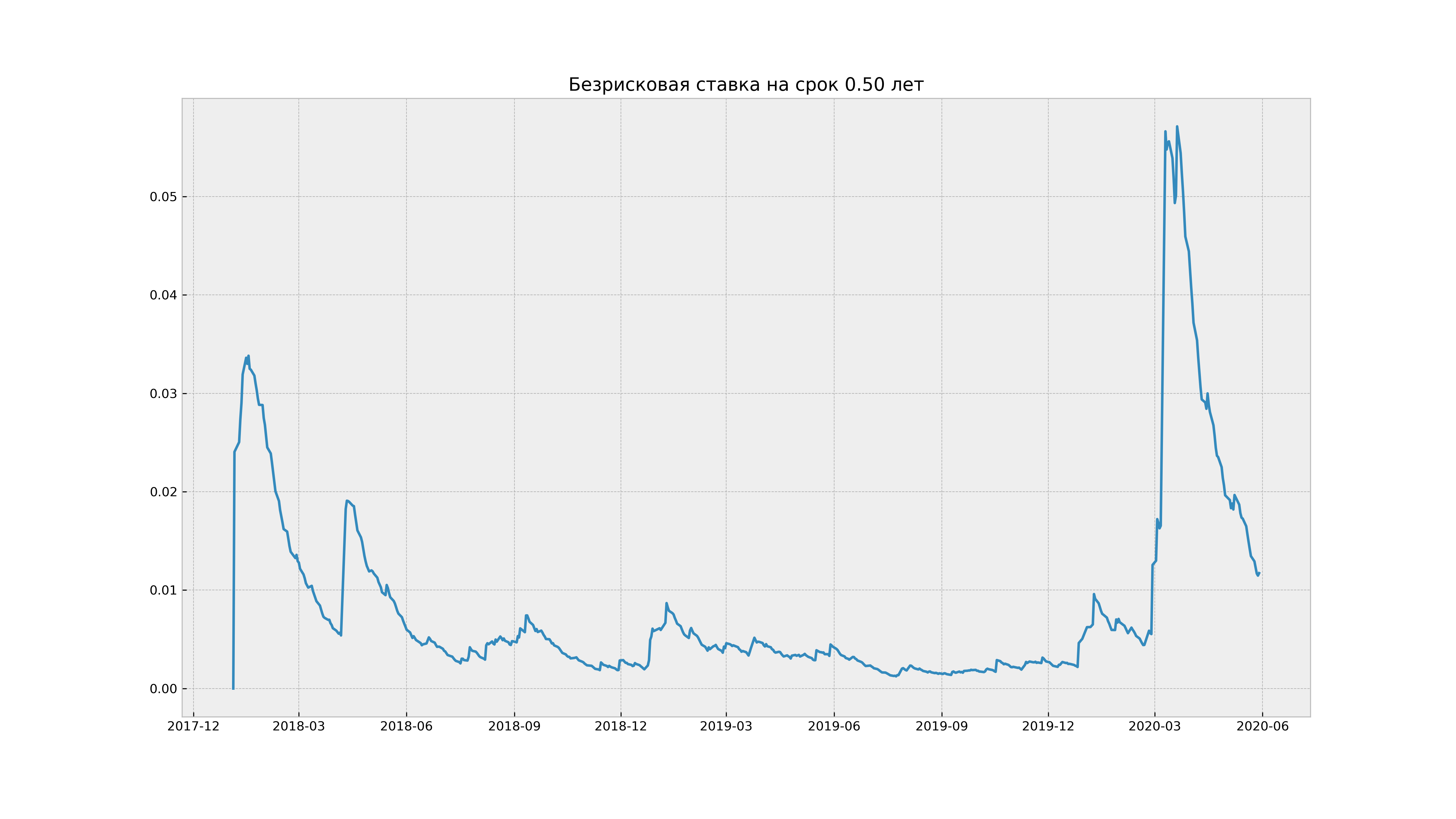
Видно, что абсолютное изменение ставки графически более похоже на стационарный процесс, чем доходность облигации, посчитанная по цене

Замечание

На самом деле тут многие возразят, что последний график мало похож на линейный. Да, это так. Однако люди, интересующиеся ситуацией на рынке, подтвердят, что март выдался достаточно неприятнымм для финансового рынка. И на графиках безрисковой ставки на различные сроки данный период как раз хорошо заметен по этим скачам на графиках. Это еще и видно на всех графиках предыдущего параграфа. Более того, например, на графиках по акциям компании Яндекс можно заметить сильные скачки и в некоторые из других дат. Это проявление реакции рынка на два исключительных события (слух о продаже большой доли акций Яндекса Сбербанку и слух о принятие закона об ограничении доли владения иностранных инвесторов в значимых онлайн-ресурсах), связанных с Яндексом за последние несколько лет. Скачки у других акций так же связаны с какими-либо событиями.
В сухом остатке, да, график не очень то и похож на линейный, но это из-за таких вот особых ситуаций. На всем остальном участке график куда больше похож на прямую, чем это проявляется у облигаций.

Итак, считаем, что $Y_{T-t}$ и есть стационарный случайный процесс. Тогда $inline$ бескупонной облигации можно рассчитать следующим образом:

$P(R < VaR) = \alpha$

$P(-dY_{T-t} < VaR) = \alpha$

$P\left(\frac{Y_{T-t}-\mu}{\sigma} > \frac{VaR+d\mu}{-d\sigma}\right) = \alpha$

$VaR = -d\mu+d\sigma \Phi^{-1}(\alpha)$

где в данном случае $\mu=E(Y_{T-t})$ , а $\sigma^2=D(Y_{T-t})$

Осталось оценить данные величины, например, способом, который был предложен при расчете матожидания и стандартного отклонения доходностей акций. Взяв исторические данные ставки на срок $inline$ лет в течение последних $inline$ дней имеем некоторый ряд $(y_0,y_1,\cdots,y_n)$ . Далее следует рассчитать абсолютное изменение ставки:

$\Delta y_t = y_t-y_{t-1}$

получив тем самым ряд $(\Delta y_1,\Delta y_2,\cdots,\Delta y_n)$ . Используя формулы

$\mu = E(Y_{T-t}) = \frac{1}{n} \sum_{t=1}^n{\Delta y_t}$

$\sigma^2 = D(Y_{T-t}) = \frac{1}{n-1} \sum_{t=1}^n{(\Delta y_t - \mu)^2}$

находим необходимые величины и затем вычисляем $inline$ бескупонной облигации на момент времени $inline$ .

Влияние спредов на ценообразование

Реальное же ценообразование бумаг фиксированной доходности на рынке немного отличается. Модель, описанная выше, соответствует ценообразованию государственных облигаций ОФЗ. Более того, кривая бескупонной доходности как раз рассчитывается исходя из цен облигаций, выпущенных государством. Иначе говоря, безрисковая ставка и есть та доходность к погашению, с которой на данный момент торгуются безрисковые облигации. Для остальных облигаций, выпущенных корпоративными (в том числе муниципальными) эмитентами, справедливая стоимость $inline$ не равна той рыночной стоимости $\hat{p_t}$ , которая образовалась на рынке на момент $inline$ . И почти всегда $\hat{p_t} < p_t$ , что означает, что участники рынка предполагают некоторый спред бумаги к безрисковым государственным инструментам, то есть они хотят некую премию за то, что берут на себя бОльший риск. Таким образом, следует учитывать данный спред. В теории данный спред можно представлять по разному в зависимости от срока до выплаты (то есть спред как и безрисковая ставка фактически может зависет и от момента времени $inline$ и от срока до выплаты $inline$ ) и есть много различных моделей спредов. Легче всего считать, что все таки спред постоянен и не зависит от срока до выплаты (и это действительно очень правдоподобное допущение). Используем эту простейшую модель. В таком случае происходит просто параллельный сдвиг кривой бескупонной доходности. Тогда справедливая стоимость выражается следующим образом:

$p_t=N\exp(-(y_{t,(T-t)}+x_t)(T-t))$

где $inline$ – спред данной бумаги в момент времени t, который в данном случае не связан со временем до погашения $inline$ .

Имеем

$r_t = \ln \frac{p_t}{p_{t-1}} = -[(y_{t,(T-t)}+x_t)(T-t)-(y_{t-1,(T-t+\boldsymbol{1})}+x_{t-1})(T-t+\boldsymbol{1})] = \\ -(d\Delta y_{t,(T-t)} + d\Delta x_t)$

В терминах случайных величин

$R = -dY_{T-t}-dX$

Первое упрощение, которое необходимо сделать для возможности дальнейших расчетов, – это принять случайные величины $Y_{T-t}$ и $inline$ за независимые. Это действительно правдоподобное предположение, так как инвесторы практически всегда котируют цену облигаций с некоторым спредом, который им кажется справедливым за тот риск, который они на себя возьмут. Этот риск связан больше с кредитоспособностью эмитента, его финансовым состоянием и другими экономическими показателями, а не с безрисковой ставкой на рынке, что как раз и дает повод считать данные случайные величины независимыми.

Далее можно поступить двумя способами:

Спред как нормальная случайная величина

Действительно считать, что спред бумаги – это случайная величина, и тогда опять делать предположение о ее распределении, если хочется оставаться в рамках параметрического метода (хотя это совсем не обязательно). Опять же предположим, что спред имеет нормальный закон распределения. При покупке или продаже облигаций важной составляющей является анализ спреда, который будет при котируемой цене, потому что если он недостаточно большой, то нет смысла брать на себя риск, связанный с этой бумагой, выгодней взять безрисковую облигацию, хоть и с чуть меньшей доходностью. Если этот спред, наоборот, чересчур большой, то такую бумагу многие захотят купить, ведь доходность стоит того риска, которую эта бумага в себе несет. Это приводит к более-менее нормальному колебанию спреда, поэтому считать данную случайную величину нормально распределенной не лишено смысла.

Тогда имеем

$P(R < VaR) = \alpha$

$P(-d(Y_{T-t} + X) < VaR) = \alpha$

$P\left(\frac{Y_{T-t}-E(Y_{T-t}+X)}{\sigma(Y_{T-t}+X)} > \frac{VaR+dE(Y_{T-t}+X)}{-d\sigma(Y_{T-t}+X)}\right) = \alpha$

$VaR = -d(\mu_{Y_{T-t}}+\mu_X)+d \sqrt{D(Y_{T-t}+X)} \Phi^{-1}(\alpha)$

Спред как константа – частный случай случайной величины

Можно считать спред конкретной бумаги константой, потому что инвесторы долгое время торгуют/котируют бумагу с одним и тем же спредом для нее, предлагаю цену покупки и продажи исключительно из соображений колебания безрисковой процентной ставки. Естественно, этот спред со временем может поменяться, например, если компания-эмитент покажет плохую годовую или квартальную отчетность или если рейтинговое агентство снизит рейтинг данной компании. Однако на достаточно стабильном и большом промежутке времени спред имеет тенденцию сохраняться, особенно если такая бумага ликвидная.

Тогда имеем

$P(R < VaR) = \alpha$

$P(-dY_{T-t} + X < VaR) = \alpha$

$P\left(\frac{Y_{T-t}-E(Y_{T-t}+X)}{\sigma(Y_{T-t}+X)} > \frac{VaR+dE(Y_{T-t}+X)}{-d\sigma(Y_{T-t}+X)}\right) = \alpha$

$VaR = -d(\mu_{Y_{T-t}}+X)+d \sigma_{Y_{T-t}} \Phi^{-1}(\alpha)$

Это особенно красивый результат, потому что в таком случае получается, что $inline$ просто сдвигается на некоторую константу. Данный факт является еще одним аргументом в пользу того, чтобы использовать мультипликатор экономического капитала, тем самым снизив сложность вычислений и технической реализации алгоритма и, как следствие, более оперативному обновлению и расчету рыночного риска портфеля в условиях часто меняющегося рынка.

Конечно же, данный результат получен исключительно для одной бескупонной облигации. В случае купонной облигации, а тем более портфеля таких бумаг, вывод становится немного сложнее, однако общая концепция остается такой же. В дальнейшем мы будем учитывать лишь безрисковую ставку при ценообразовании облигаций, скинув бремя корректировки окончательного результата на мультипликатор рыночного капитала, а за основную формулу расчета $inline$ возьмем чуть менее сложный вариант.

Расчет VaR для купонной облигации

В случае купонной облигации, к сожалению, такой красивый и простой переход от цены бумаги к ее доходности неосуществим. Действительно, теперь справедливая цена на момент времени $inline$ выражается следующим образом:

$p_t=\sum_{i=1}^{k}{C_{T_i}\exp(-y_{t,(T_i-t)}(T_i-t)})$

где $C_{T_i}$ – купонная выплата в момент времени $inline$ , $C_{T_k}=C$ – номинал облигации. Поэтому в данной ситуации при переходе к доходности купонной облигации приходится поступать одним из следующих двух способов:

Портфель бескупонных облигаций

Представим данную купонную облигацию как портфель бескупонных. То есть каждый купон по такой облигации – это одна бескупонная облигация. Доходность $inline$ -ой бескупонной облигации обозначим за $R_i=d_i Y_{T_i-t}$ , а вес $inline$ -ой бескупонной облигации обозначим за

$w_i = \frac{C_{T_i}\exp(-y_{t,(T_i-t)}(T_i-t))} {\sum_{j=1}^{k}{C_{T_j}\exp^{-y_{t,(T_j-t)}(T_j-t)}}}$

То есть, как и в случае портфеля акций имеется вектор доходностей $\boldsymbol{R} = (R_1,R_2,\cdots,R_k )^ = (d_1 Y_{T_1-t},d_2 Y_{T_2-t},\cdots,d_k Y_{T_k-t})^T = \boldsymbol{d} \circ \boldsymbol{Y}$ (случайный вектор), где $\boldsymbol{d} = (d_1,d_2,\cdots,d_k )^T$ – вектор периодов до выплат купонов, $\boldsymbol{Y}= (Y_{T_1-t},Y_{T_2-t},\cdots,Y_{T_k-t})^T$ (случайный вектор) – абсолютные изменения ставок на соответствующие сроки, а операция $\circ$ — произведение Адамара-Шура (покомпонентное произведение), и вектор весов $\boldsymbol{w} = (w_1,w_2,…,w_k )^T$ . Тогда формулы для матожидания и стандартного отклонения доходности портфеля бумаг будут выглядеть следующим образом:

$\mu = E(R) = \boldsymbol{w}^T E(\boldsymbol{R})=\boldsymbol{w}^T (\boldsymbol{d} \circ \boldsymbol{\mu})$

$\sigma^2 = D(R) = \boldsymbol{w}^T(\boldsymbol{dd_T} \circ \boldsymbol{C})\boldsymbol{w}$

где $\boldsymbol{\mu} = (\mu_1,\mu_2,\cdots,\mu_k ) = E(Y)=(E(Y_{T_1-t}),E(Y_{T_2-t}),\cdots,E(Y_{T_k-t}))$ – вектор матожиданий, а

$\boldsymbol{C} = \begin{pmatrix} Cov(Y_{T_1-t},Y_{T_1-t}) & Cov(Y_{T_1-t},Y_{T_2-t}) & \cdots & Cov(Y_{T_1-t},Y_{T_k-t}) \\ Cov(Y_{T_2-t},Y_{T_1-t}) & Cov(Y_{T_2-t},Y_{T_2-t}) & \cdots & Cov(Y_{T_2-t},Y_{T_k-t}) \\ \cdots & \cdots & \cdots & \cdots \\ Cov(Y_{T_k-t},Y_{T_1-t}) & Cov(Y_k,Y_{T_2-t}) & \cdots & Cov(Y_{T_k-t},Y_{T_k-t}) \end{pmatrix}$

-ковариационная матрица абсолютных изменений ставок.

Линейное приближение

Другой способ – это представить доходность купонной облигации как линейное приближение изменения ставки. Известно, что

$r_t \approx \frac{d}{1+\rho} \Delta y_{t,(T-t)} = -\tilde{d} \Delta y_{t,(T-t)}$

где $\rho$ – доходность облигации к погашению (YTM), $\tilde{d}$ – модифицированная дюрация.
Однако тут возникает вопрос: какую ставку брать в таком случае? То есть на какой срок должна быть ставка, по которой и будут последующие оценки статистических характеристик? Придется прибегнуть к некоторой эвристике. Вспомним смысл дюрации $inline$ – это средневзвешенный срок потока платежей. То есть в среднем все выплаты произойдут через $inline$ лет. Тогда и ставку логично взять на срок, равный $inline$ годам. То есть тогда имеем

$r_t \approx -\tilde{d} \Delta y_{t,d}$

В данном способе расчета интуитивно происходит усреднение выплат по времени. Дальнейшая же идея расчета $inline$ остается аналогична той, которая использовалась для бескупонной облигации.
Стоит обратить внимание, что в данной формуле ставку мы берем на срок $inline$ лет, а коэффициент линейного приближения равен $\tilde{d}$ – модифицированной дюрации, а не самой дюрации. Итак, окончательно:

$R = -\tilde{d} Y_d$

$VaR = -\tilde{d} \mu + \tilde{d} \sigma \Phi^{-1} (\alpha)$

Естественно предположить, что первый способ расчета – разложение купонной облигации по потокам платежей – даст результат точнее. Ведь так мы не пренебрегаем временем до этих платежей и не усредняем их, а следовательно, и сохраняем больше информации, однако у такого способа есть свои недостатки, которые рассмотрим позже.

Расчет VaR для портфеля купонных облигаций

Для портфеля купонных облигаций можно поступить аналогичным образом. Либо представить каждую купонную облигацию в портфеле как несколько бескупонных, либо для каждой купонной облигации брать линейное приближение.

Портфель бескупонных облигаций

В первом случае мы рассматриваем всевозможные платежи, которые будут по бумагам в портфеле и, соответственно, работаем с ними как с бескупонными облигациями.

Итак, в таком случае у нас будет n бумаг в портфеле, $inline$ -ая из которых имеет $inline$ платежей, которые мы обозначим за $C_{T_j,i}$ , где индекс следует понимать как «платеж в момент времени $inline$ , $inline$ -ой бумаги в портфеле». Тогда вес каждого платежа:

$w_{ji} = \frac{N_i C_{T_j,i} \exp(-y_{t,(T_j-t)} (T_j-t))} {\sum_{i=1}^n {N_i \sum_{j=1}^{k_i}{C_{T_j,i} \exp(-y_{t,(T_j-t)}(T_j-t))}}}$

где $inline$ – количество $inline$ -ой облигаций в портфеле.

Имеем вектор доходностей $\boldsymbol{R} = (R_{11},\cdots,R_{k_1 1},R_{12},\cdots,R_{k_2 2},\cdots,R_{1n},\cdots,R_{k_n n})^T = \boldsymbol{d} \circ \boldsymbol{Y}$ и вектор весов $\boldsymbol{w} = (w_{11},\cdots,w_{k_1 1},w_{12},\cdots,w_{k_2 2},\cdots,w_{1n},\cdots,w_{k_n n})^T$ . Окончательно:

$\mu = E(R) = \boldsymbol{w}^T E(\boldsymbol{R}) = \boldsymbol{w}^T \boldsymbol{(d \circ \mu)}$

$\sigma^2 = D(R) = \boldsymbol{w}^T (\boldsymbol{dd^T} \circ \boldsymbol{C}) \boldsymbol{w}$

Однако возникает одна проблема. Дело в том, что матрица $\boldsymbol{C}$ в данном случае имеет размерность $(k_1+\cdots+k_n)\times(k_1+\cdots+k_n)$ . Конечно даже такие матрицы неплохо считаются на современных компьютерах, но в таком случае разумнее просто прибегнуть к разложению денежных потоков на стандартные сроки о которой подробнее будет сказано позже.

Линейное приближение

Во втором случае для каждой облигации мы используем линейное приближение. Опять же, пусть в портфеле $inline$ облигаций. Доходность $inline$ – ой облигации

$R_i = -\tilde{d_i}Y_{d_i}$

Снова имеем вектор доходностей $\boldsymbol{R} = (R_1,R_2,\cdots,R_n)^T = (\tilde{d_1}Y_{d_1},\tilde{d_2}Y_{d_2} ,\cdots,\tilde{d_n}Y_{d_n})^T = \boldsymbol{\tilde{d}} \circ \boldsymbol{Y}$ и вектор весов $\boldsymbol{w} = (w_1,\cdots,w_n)^T$ , где

$w_i = \frac{N_i \left(\sum_{j=1}^{k_i}C_{T_j,i} \right) \exp(-y_{t,d_i} \tilde{d_i})} {\sum_{i=1}^n{N_i \left(\sum_{j=1}^{k_i}C_{T_j,i} \right) \exp(-y_{t,d_i} \tilde{d_i}})}$

В данном случае действовать стоит полностью по аналогии расчета $inline$ для купонной облигации в случае, когда мы считали такую купонную облигацию как портфель бескупонных. Единственное отличие, о котором просто следует помнить – это другие коэффициенты линейного приближения – модифицированные дюрации.

Заключение

Были представлены основные идеи, теоретические основы и методы построения математической модели оценки рыночного риска портфеля облигаций. Ее применение на модельных и реальных данных будет представлено в следующей части. Будет уже существенно меньше математики и основное внимание уделим проблемам, возникающим в жизни при вычислении рыночного риска реального портфеля.

Что почитать

Бабайцев В.А., Гисин В.Б. Математические методы финансового анализа: учебное пособие. М.: Финансовая академия, 2005.
Балабушкин А. и др. (ММВБ, Банк России) Кривая бескупонной доходности на рынке ГКО-ОФЗ //Рынок ценных бумаг. – 2006. – №. 3. – С. 306.
Крылова В. Z-спрэд и его братья, Ренессанс Капитал – Количественный анализ, Долговые обязательства, Россия – 30 октября 2006 г.
Методика определения Кривой бескупонной доходности государственных облигаций – ПАО Московская Биржа, 2017. – 14 с.
J.P.Morgan & Co., Inc., RiskMetrics Technical Document, 4th edition, December, 1996.

Благодарности

Сама работа выполнена мной достаточно давно (начало 2018 года), но публиковать ее я решил только сейчас. Хочу выразить благодарность тем, кто помогал мне в ходе работы, а именно

Сотрудникам АО "УК ТФГ" и в особенности сотрудникам отдела "Управление анализа и контроля рисков" Задонской Екатерине и Майоровой Елене
Сотруднику Финансового университета при Правительстве РФ, профессору, к.ф.-м.н, Гисину Владимиру Борисовичу

Tags:

Hubs:

If this publication inspired you and you want to support the author, do not hesitate to click on the button