Мы представляем Yao (статья), пакет с открытым исходным кодом Julia для решения практических задач в исследованиях квантовых вычислений. Имя Yao происходит от первого китайского иероглифа, означающего унитарность (幺正).

Зачем мы создали Yao? Короче говоря, мы такие же жадные, как и те ребята, что создавали язык Julia. Мы хотим таких штук, как:
Дифференцируемость
В блоге Julia (а также в статье о Zygote), часто проскакивает мысль, что градиенты иногда могут быть лучшим программистом, чем люди. В квантовых вычислениях они могут быть использованы для вариационных алгоритмов, квантового управления, обучения вентилей и т.д. Таким образом, мы хотим иметь дифференцируемое программирование и на квантовых схемах!
Однако автоматическое дифференцирование (AD) для квантовых схем сильно отличается от обычных программ: стоимость выделения памяти при моделировании схем может быть чрезвычайно высокой из-за кэширования промежуточных состояний в общем контексте. А в прямом режиме AD нам нужна дополнительная семантика, чтобы сохранить квантовую схему – так, чтобы она могла быть реализована на реальном устройстве.
В Yao для достижения этой цели мы внедрили встроенный доменно-специфичный механизм автоматического дифференцирования (AD), чтобы использовать обратимую природу квантовых схем. Ниже приведен пример вариационного квантового алгоритма поиска собственных значений. С помощью нашего эффективного AD движка вы сможете попробовать его на своем ноутбуке
n, d = 16, 100
circuit = dispatch!(variational_circuit(n, d),:random);
h = heisenberg(n)@time for i in 1:100
_, grad = expect'(h, zero_state(n) => circuit)
dispatch!(-, circuit, 1e-1 * grad)
println("Step $i, energy = $(real.(expect(h, zero_state(n)=>circuit)))")
endЭтот пример обучает 100-слойную параметризованную схему (4816 параметров), чтобы найти основное состояние 16-узловой модели Гейзенберга. Движок также может быть легко интегрирован с общей AD платформой, такой как Zygote, как в примере обучения гейта (вентиля). Мы используем дифференцируемое программирование, чтобы найти разложение данного унитарного объекта. Вы можете узнать больше в нашем учебнике и зоопарке квантовых алгоритмов.
Расширяемость
Новые исследовательские идеи появляются каждый день и каждый час. То же поле софта на квантовых вычислениях плодоносит со все нарастающей силой. Мы хотим, чтобы структура была достаточно гибкой для исследователей и разработчиков, чтобы была возможность расширить ее на любом уровне для любого возможного типа исследований.
Во-первых, мы спроектировали и разработали аппаратно-свободное промежуточное представление (промежуточное представление квантового блока, QBIR) для представления и манипулирования квантовыми схемами и набором квантовых регистровых интерфейсов. Эта конструкция позволяет расширить Yao до индивидуальных алгоритмов, аппаратного обеспечения и многого другого, перегружая соответствующие интерфейсы. Например, при достижении самой современной производительности, как показано в следующем разделе, мы расширяем наш бэкэнд CUDA в CuYao всего несколькими сотнями строк кода, написанного на родном языке Julia с помощью CUDAnative. С некоторыми патчами и синтаксическим сахаром Yao запросто срабатывается с символическим движком SymEngine, что позволяет дифференцировать и вычислять квантовые схемы символьно.
Во-вторых, как и другие проекты в Julia, мы делаем Yao расширяемым на уровне архитектуры. Пакет Yao (или его CUDA-окружение CuYao) — это всего лишь мета-пакет, который реэкспортирует другие пакеты компонентов. Разработчики могут настроить свое собственное программное обеспечение с помощью легких зависимостей и быстро разрабатывать новые функции.
Эффективность
Эффективность также имеет особое значение в исследованиях, которые развивают численные эксперименты, такие как вариационные квантовые алгоритмы. Помимо всех других интересных функций, мы все еще хотим, чтобы этот фреймворк достигал самой современной производительности во время симуляций.
Используя нативное программирование на графическом процессоре в сочетании с специализацией, основанной на множественной диспетчеризации, Yao достигает самых современных характеристик на квантовых схемах среднего размера.

Более детальный бенчмарк вы можете посмотреть здесь.
Что дальше?
Пока что мы рады объявить о рождении проекта, но путешествие только начинается.
Мы все еще хотим актуальной аппаратной компиляции (например, OpenQASM), упрощения схем и компиляции (YaoIR), визуализации, тензорных сеток (смотрите в песочнице) и многого другого!
Хотя некоторые бета-пользователи помогли нам сформировать это программное обеспечение во время реальной исследовательской работы, нам все еще нужно больше вариантов использования и больше людей, чтобы развиваться дальше. Если вы заинтересованы в этой идее, присоединяйтесь к нам, и давайте создадим мощный инструмент для исследования квантовых вычислений!
Конец перевода статьи из блога официального сайта Julia.
Теперь же будет интересно опробовать всю эту красоту на своей машине.
] dev https://github.com/QuantumBFS/QuAlgorithmZoo.jl.gitusing Pkg
pkgs = ["Plots", "Flux", "Yao", "YaoExtensions", "StatsBase", "BitBasis", "FFTW", "SymEngine"]
for p in pkgs
Pkg.add(p)
end
using Yao, YaoExtensions, Plots, StatsBaseГотовим состояние Гринбергера-Хорна-Цайлингера

Состояние GHZ — это определенный тип запутанного квантового состояния, который включает по меньшей мере три подсистемы (состояния частиц или кубиты). Кстати, для экскурса можно предложить ряд ресурсов:
- Есть две функции — пост с мягким введением в линейную алгебру квантовых вычислений
- Квантовая песочница: часть 2 — набор простых аналогий для понимания сути векторов состояния (читать вместе с комментами)
- Основы квантовых вычислений — блог компании мелкомягких, в котором раскрыты основные обозначения, а также имеется введение в язык Q#
Для более глубокого погружения:
- Квантовые вычисления и функциональное программирование — небольшое пособие с минимумом формул от программиста программистам. Кого-то могут отпугнуть листинги на хаскеле, но их понимание не критично, да и чем не повод изучить еще один язык, к тому же, функциональный. Особенно хотелось бы выделить обзор основной литературы по теме: статьи, книги, курсы — все, что было актуально на момент написания.
- Квантовые вычисления и квантовая информация М. Нильсен, И. Чанг — библия нашей эпохи. Детальный ликбез в линейную алгебру, квантовую механику, информатику, теорию вероятности, с последующим переходом к квантовым вычислениям и реализациям в железе. Написана живым языком, формул ровно столько, сколько необходимо, вообщем, крайне рекомендую не только тем, кто собирается втягиваться в квантовые вычисления, но и каждому более-менее технически подкованному человеку.
- Введение в квантовые вычисления. Квантовые алгоритмы С. С. Сысоев — хорошо проработанное пособие с разбором алгоритмов и задачами (также будет полезен бесплатный авторский курс).
- Quirk — конструктор квантовых схем онлайн
Ну и общий совет по обучению: лучше штудировать параллельно несколько книг, чтобы рассматривать проблемы с разных ракурсов, и закреплять выполнение практическими заданиями. Даже если кажется, что перспектива квантового разработчика в IBM вам не светит, в любом случае, это довольно интересная область, да и обучение будет хорошей профилактикой кристализации мышления и всяких деменций.
Итак, пока мы обсуждали литературу, все что нужно скачалось и установилось, а значит пора приступать проектированию квантовых схем! В общем виде, рецепт приготовления ГХЦ-состояния выглядит так:
Для четырех кубитов схема принимает вид

а на языке Yao:
circuit = chain(
4,
put(1=>X),
repeat(H, 2:4),
control(2, 1=>X),
control(4, 3=>X),
control(3, 1=>X),
control(4, 3=>X),
repeat(H, 1:4),
)nqubits: 4
chain
├─ put on (1)
│ └─ X gate
├─ repeat on (2, 3, 4)
│ └─ H gate
├─ control(2)
│ └─ (1,) X gate
├─ control(4)
│ └─ (3,) X gate
├─ control(3)
│ └─ (1,) X gate
├─ control(4)
│ └─ (3,) X gate
└─ repeat on (1, 2, 3, 4)
└─ H gateТут всё как написано, так и работает: на первый провод сажается вентиль X, он же not-gate (переворот на сфере Блоха), на остальные прицепляются Адамары, а далее раскидываются cnot-вентили.
Теперь можно по проводам отправлять кубиты и проводить измерения (многократные, ведь тут царит сплошная статистика)
results = ArrayReg(bit"0101") |> circuit |> r->measure(r, nshots=1000)
hist = fit(Histogram, Int.(results), 0:16)
bar(hist.edges[1] .- 0.5, hist.weights, legend=:none)
При таком раскладе, ГХЦ-состояние коллапсирует в или
.
Квантовое преобразование Фурье
Еще одна полезная штука из мира унитарных операторов — это КПФ:

схема для трех кубитов
Здесь
оператор, управляющий фазовым сдвигом гейта.
Схема квантового преобразования Фурье (QFT) состоит в том, чтобы повторять два вида блоков:

для пяти кубитов
Давайте определим блок А и блок B (A является блоком управления):
A(i, j) = control(i, j=>shift(2π/(1<<(i-j+1))))
R4 = A(4, 1)
# (n -> control(n, 4, 1 => shift(0.39269908169872414)))После того, как вы построите блок, вы можете проверить его матрицу с помощью функции mat. Давайте построим схему блока A и посмотрим матрицу вентиля :
R4(5)
#nqubits: 5
#control(4)
#└─ (1,) shift(0.39269908169872414)mat(R4(5))32×32 LinearAlgebra.Diagonal{Complex{Float64},Array{Complex{Float64},1}}:
1.0+0.0im ⋅ ⋅ ⋅ … ⋅ ⋅
⋅ 1.0+0.0im ⋅ ⋅ ⋅ ⋅
⋅ ⋅ 1.0+0.0im ⋅ ⋅ ⋅
⋅ ⋅ ⋅ 1.0+0.0im ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ … ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ … ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋮ ⋱ ⋮
⋅ ⋅ ⋅ ⋅ … ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ … ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
⋅ ⋅ ⋅ ⋅ … 1.0+0.0im ⋅
⋅ ⋅ ⋅ ⋅ ⋅ 0.92388+0.382683imЗатем мы повторяем этот блок управления снова и снова на разных кубитах и помещаем гейт Адамара в i-й кубит, чтобы построить i-й блок B. К тому же, нам нужно ввести здесь общее число кубитов n, потому что мы должны перебирать их от k-го местоположения до последнего.
Теперь давайте построим схему, связав все блоки B вместе
B(n, k) = chain(n, j==k ? put(k=>H) : A(j, k) for j in k:n)
qft(n) = chain(B(n, k) for k in 1:n)
qft(4)nqubits: 4
chain
├─ chain
│ ├─ put on (1)
│ │ └─ H
│ ├─ control(2)
│ │ └─ (1,) shift(1.5707963267948966)
│ ├─ control(3)
│ │ └─ (1,) shift(0.7853981633974483)
│ └─ control(4)
│ └─ (1,) shift(0.39269908169872414)
├─ chain
│ ├─ put on (2)
│ │ └─ H
│ ├─ control(3)
│ │ └─ (2,) shift(1.5707963267948966)
│ └─ control(4)
│ └─ (2,) shift(0.7853981633974483)
├─ chain
│ ├─ put on (3)
│ │ └─ H
│ └─ control(4)
│ └─ (3,) shift(1.5707963267948966)
└─ chain
└─ put on (4)
└─ HВ большинстве случаев, таких функций как A и B достаточно, чтобы обернуть квантовые схемы, но иногда нам нужно отправить специализированные методы на определенные виды квантовых схем, или мы хотим определить внешний блок для экспорта, поэтому полезно иметь возможность обернуть схему в пользовательские блоки.

Во-первых, мы определяем новый тип как подтип PrimitiveBlock, так как мы не собираемся использовать подблоки QFT. Если вам нужно использовать его подблоки, то лучше определить его под CompositeBlock.
struct QFT{N} <: PrimitiveBlock{N} end
QFT(n::Int) = QFT{n}()
# определяем схему
circuit2(::QFT{N}) where N = qft(N)
# и строим матрицу по схеме
YaoBlocks.mat(::Type{T}, x::QFT) where T = mat(T, circuit2(x))
YaoBlocks.print_block(io::IO, x::QFT{N}) where N = print(io, "QFT($N)")
using FFTW, LinearAlgebra
function YaoBlocks.apply!(r::ArrayReg, x::QFT)
α = sqrt(length(statevec(r)))
invorder!(r)
lmul!(α, ifft!(statevec(r)))
return r
endТакже мы перегрузили print_block чтобы воспроизводить содержимое по своему, и попутно добавили имитацию QFT используя старое доброе быстрое Фурье преобразование. А теперь пустим по проводам произвольные состояния, чтобы удостовериться, что все корректно работает
r = rand_state(5)
r1 = r |> copy |> QFT(5)
r2 = r |> copy |> circuit2(QFT(5))
r1 ≈ r2
# true
Алгоритм Шора
Да, тот самый, который взломает все наши приватные ключи. Схема довольно проста

Основная программа алгоритма Шора может быть имплементирована в несколько строк кода. Для теоретической части, пожалуйста, обратитесь к справочным материалам (также объяснение можно найти в большинстве книг и пособий). Наш вариант факторизует целое число L и возвращает один из множителей. Здесь, ввод ver может быть либо Val(:quantum) либо Val(:classical), чтоб можно было сравнить с классическим вариантом.
using Yao, BitBasis
using YaoExtensions: KMod, QFTCircuit
using QuAlgorithmZoo: NumberTheory
function shor(L::Int, ver=Val(:quantum); maxtry=100)
L%2 == 0 && return 2
# find short cut solutions like `a^b`
res = NumberTheory.factor_a_power_b(L)
res !== nothing && return res[1]
for i in 1:maxtry
# step 1
x = NumberTheory.rand_primeto(L)
# step 2
r = get_order(ver, x, L; )
if r%2 == 0 && powermod(x, r÷2, L) != L-1
# step 3
f1, f2 = gcd(powermod(x, r÷2, L)-1, L), gcd(powermod(x, r÷2, L)+1, L)
if f1!=1
return f1
elseif f2!=1
return f2
else
error("Algorithm Fail!")
end
end
end
endНе вдаваясь в подробности, каждую итерацию можно описать простым набором шагов:
Случайным образом выбрать число, которое является взаимно простым для
L, т. е.gcd(x, L) == 1. Сложность этого алгоритма полиномиальна.
Получить порядок x, т. е. находим число r, удовлетворяющее
mod(x^r, L) == 1. Если r четно, а x^(r÷2) нетривиально, продолжить, иначе произвести еще одну попытку. Здесь тривиальное, это равноеL-1 (mod L).
Согласно теореме 5.2 в книге Нильсена,
кто-то изgcd(x^(r÷2)-1, L)иgcd (x^(r÷2)+1, L)должен быть нетривиальным (!=1) коэффициентом L. обратите внимание, чтоpowermod(x, r÷2, L)должен быть равен -1, а не 1, в противном случае порядок должен бытьr/2в соответствии с определением.
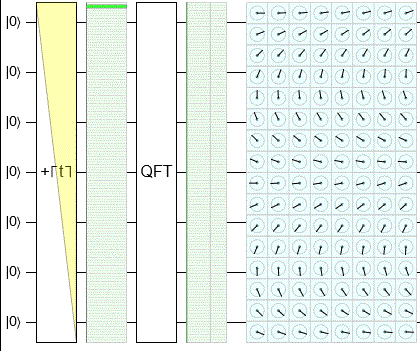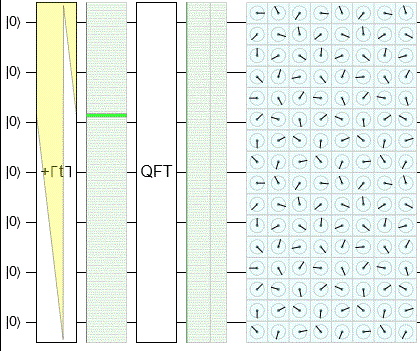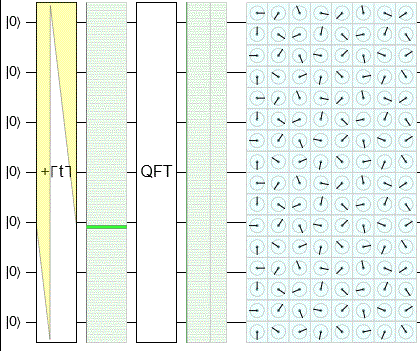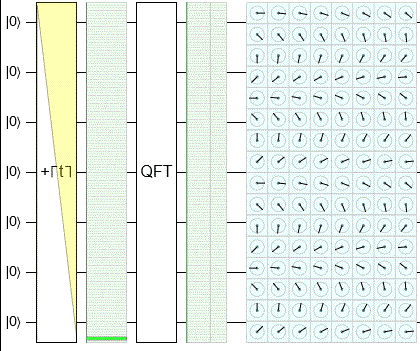
Единственное различие между классической и квантовой версией — это алгоритм нахождения порядка. Мы предоставили классический алгоритм поиска порядка в NumberTheory, здесь мы сосредоточимся на квантовой версии. Алгоритм заключается в следующем
- Запустить схему, чтобы получить битовую строку
- интерпретировать эту битовую строку в выходном регистре как рациональное число s / r. Чтобы достичь этого, мы сначала интерпретируем его как число с плавающей точкой, а затем алгоритм непрерывной дроби может найти для нас наилучшее соответствие.
При использовании квантовой версии у нас есть гибкость для установки ключевых слов-аргументов nshot, nbit (размер регистра входных данных) и ncbit (размер управляющего регистра или выходного регистра). nbit можно просто выбрать в качестве минимального размера регистра для хранения входных данных, в то время как ncbit можно оценить с помощью следующей функции
"""оценка необходимого размера выходного регистра."""
estimate_ncbit(nbit::Int, ϵ::Real) = 2*nbit + 1 + ceil(Int,log2(2+1/2ϵ))
get_order(::Val{:classical}, x::Int, L::Int; kwargs...) = NumberTheory.find_order(x, L)
function get_order(::Val{:quantum}, x::Int, L::Int; nshots::Int=10,
nbit::Int=bit_length(L-1), ncbit::Int=estimate_ncbit(nbit, 0.25))
c = order_finding_circuit(x, L; nbit=nbit, ncbit=ncbit)
reg = join(product_state(nbit, 1), zero_state(ncbit))
res = measure(copy(reg) |> c; nshots=nshots)
for r in res
# split bit string b into lower bits `k` and higher bits `r`.
mask = bmask(1:ncbit)
k,i = r&mask, r>>ncbit
# get s/r
ϕ = bfloat(k) #
ϕ == 0 && continue
# order_from_float: given a floating point number,
# return the closest rational number with bounded number of continued fraction steps.
order = NumberTheory.order_from_float(ϕ, x, L)
if order === nothing
continue
else
return order
end
end
return nothing
endorder_finding_circuit(x::Int, L::Int; nbit::Int=bit_length(L-1), ncbit::Int=estimate_ncbit(nbit, 0.25)) -> AbstractBlock
Возвращает схему для нахождения порядка x по отношению к L,
подавая входной сигнал |1>⊗|0> и получая результирующий квантовый регистр с нужной "фазовой" информацией.
function order_finding_circuit(x::Int, L::Int; nbit::Int, ncbit::Int)
N = nbit+ncbit
chain(N, repeat(N, H, 1:ncbit), KMod{N, ncbit}(x, L),
subroutine(N, qft_circuit(ncbit)', 1:ncbit))
endСхема поиска порядка состоит из трех частей
- Вентили Адамара
KModкоторый считает классическую функциюmod(a^k*x, L).
k— это целое число, хранящееся в первыхk(илиncbit) кубитах, а остальныеN-Kкубиты хранятa. обратите внимание, что это не базовый гейт, он должен был быть скомпилирован в несколько элементов, что на данный момент не реализовано в Yao. Чтобы узнать больше о реализации арифметики на квантовой схеме, пожалуйста, прочтите эту статью.- Обратное квантовое преобразование Фурье.
Ну чтож, разложим-ка на множители какое-нибудь число:
@time shor(35, Val(:quantum))
# 2.287219 seconds (14.37 k allocations: 113.341 MiB, 1.38% gc time)
# 5@time shor(35, Val(:classical))
# 0.000208 seconds (6 allocations: 224 bytes)
# 5
Итог
Таким образом, сегодня мы обкатали мощный и удобный инструмент для квантовых вычислений. Для дальнейшего обучения следует разобраться с остальными примерами: алгоритм поиска от Гровера, машина Борна, девятикубитная схема коррекции ошибки и т.д. Далее закрепляем материал, выполняя практические задания из приведенных выше методичек, может даже будет возможность поучаствовать в различных конкурсах.
И всегда имеем в виду, что квантовые вычисления могут произвести очередную революцию, посему следует быть готовым заранее.
