Для начала, давайте разберемся с двумя важнейшими эпидемиологическими понятиями: смертностью и летальностью. Сразу оговорюсь, что в википедии (как русской, так и английской) приведено ошибочное определение летальности, которое сбивает с толку.
Летальность — это вероятность умереть, если у пациента диагностирована болезнь. Вот цитата из научной статьи:
Смертность — это отношение числа умерших от болезни к размеру популяции за какой-то промежуток времени. Обычно, считают сколько смертей на 100 тыс. населения за единицу времени. Смертность непосредственно связана с летальностью: это произведение вероятности заболеть (за определенный временной период) на летальность. В самом деле, для того, чтобы умереть от болезни надо сначала ей заразиться, а потом уж, если не повезет…
Высокая летальность не означает автоматически, что смертность тоже высокая. Например, болезнь убивает с вероятностью 1, но поражает всего 0.1% населения, скажем, за год (похожим образом ведет себя вирус Эболы, к примеру). Тогда смертность составит всего 1/1000. В то время как болезнь с летальностью в сто раз меньше (0.01) может иметь в 10 раз более высокую смертность (1/100), если поражает все население за тот же период.
Смертность явно зависит от времени — со временем количество инфицированных, как правило, увеличивается, поэтому и смертность растет. Летальность же от времени не зависит явным образом, но, например, может снизиться со временем, если найдут/изобретут лекарство.
Можно еще сказать, что летальность это условная вероятность смерти при условии болезни, а смертность — это вероятность умереть от болезни за какой-то временной промежуток.
Летальность, в свою очередь, подразделяется на Case Fatality Ratio (CFR) и Infection Fatality Ratio (IFR):
CFR — это летальность, рассчитанная по подтвержденным случаям. У этого показателя есть подводный камень: в первую очередь обычно тестируют тех, у кого ярко выражены симптомы. Поэтому можно сказать, что в первом приближении CFR — это вероятность смерти при условии наличия болезни и выраженных симптомов.
IFR — это и есть летальность, то есть вероятность смерти при наличии болезни. Этот показатель включает также легкие и бессимптомные случаи болезни и поэтому может быть намного меньше чем CFR. Точно рассчитать этот показатель практически невозможно, потому что мало кто станет тестировать все население, чтобы учесть и бессимптомных носителей тоже, но его можно оценить.
В эпидемиологии крайне важно уметь в начале эпидемии оценить летальность, чтобы иметь возможность принять меры, сообразные тяжести заболевания. К сожалению, сделать это чрезвычайно сложно и сейчас мы узнаем почему.
Одним из наиболее популярных методов оценки летальности является простая формула: Deaths / Cases, то есть количество смертей от болезни поделить на общее число инфицированных к текущему моменту. К сожалению, эта весьма популярная оценка (называемая также наивным методом) обладает врожденным недостатком, который иллюстрируется следующим примером:
Эта недооценка наивного метода приводит к ложным спекуляциям. Например, во время эпидемии SARS наивная оценка росла со временем, порождая слухи о том, что вирус эволюционирует, превращаясь в более смертоносного убийцу. А причиной этого является простая математика: рост количества заболевших замедляется, что уменьшает недооценку летальности наивным эстиматором.
Таким образом, можно сказать, что наивный метод недооценивает летальность, уменьшая ее в раз, где
раз, где  — это время от заражения до смерти, а b — параметр, характеризующий время удвоения количества зараженных. Но, к сожалению, такая поправка плохо работает в реальной жизни, потому что пациенты умирают не строго через определенный промежуток времени организованными группами, а случайным образом. Давайте учтем это и выведем формулу поправки, которая будет применима в реальной жизни.
— это время от заражения до смерти, а b — параметр, характеризующий время удвоения количества зараженных. Но, к сожалению, такая поправка плохо работает в реальной жизни, потому что пациенты умирают не строго через определенный промежуток времени организованными группами, а случайным образом. Давайте учтем это и выведем формулу поправки, которая будет применима в реальной жизни.
А теперь попробуем оценить этот bias для оценки летальности в ранний период развития эпидемии коронавирусной инфекции в китайском городе Ухань. Для этого воспользуемся следующими предположениями: время удвоения числа заболевших равно 5 дням, а среднее время от регистрации до смерти равно 18 дням.
Еще предположим, что день смерти имеет распределение Пуассона:
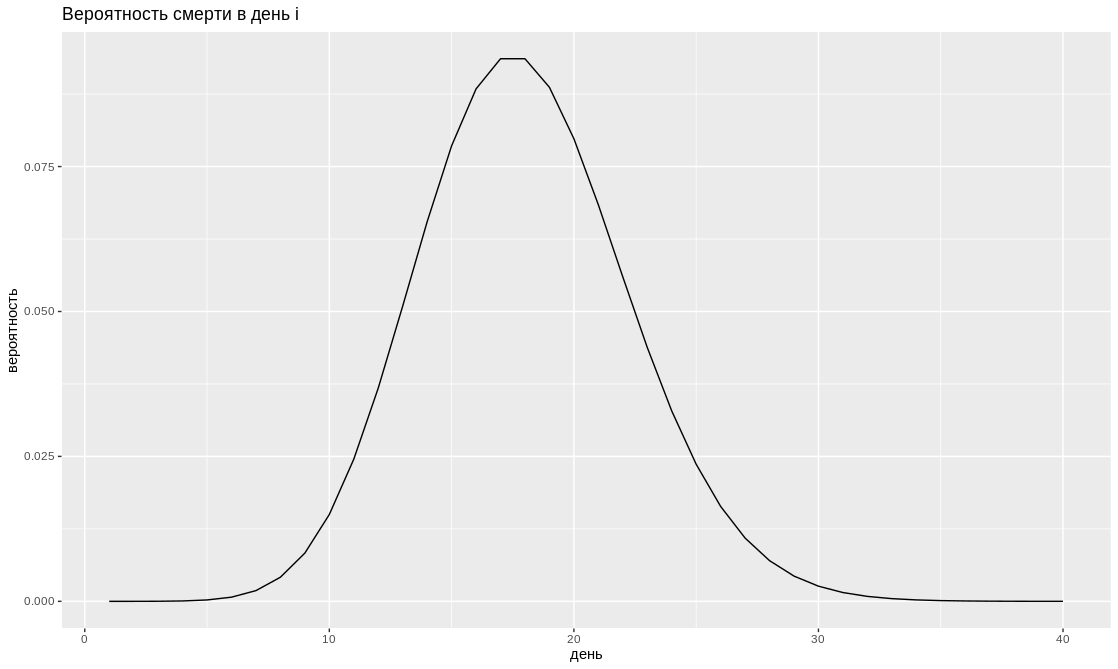
Подставив значения в формулу, получим, что наивный метод занижает летальность примерно в 9 раз. Таким образом, CFR по подтвержденным случаям составляет около 18%! Подчеркиваю, что CFR не включает недокументированных пациентов, количество которых оценили китайские ученые: по их модели, 86% случаев были не зарегистрированы. Это позволяет нам вычислить IFR: IFR = 0.14*CFR = 2.5%. Эти оценки прекрасно согласуются с оценками CFR (18%, 11%-81%), и IFR (1%, 0.5%-4%), которые были получены специалистами Imperial College London.
Важно понимать, что значение IFR не следует использовать для оценки вероятности умереть от болезни, так как вероятность умереть от болезни зависит от множества факторов:
Тогда для чего же так важно знать IFR хотя бы приблизительно? Это нужно знать для того, чтобы иметь возможность сравнить с известными заболеваниями. Например, летальность (IFR) гриппа составляет 0.01%, что, как минимум, в десятки раз ниже. С учетом того, факта, что коронавирус более заразный (R0 > 2 против примерно 1.3 у гриппа), это может привести к десяткам миллионов смертей по всему миру, так как грипп может уносить до 650 000 жизней в год. Поэтому ни в коем случае не стоит считать, что «это просто грипп».
Данная статья имеет следующие цели: объяснить в чем различие между смертность и летальностью, объяснить, что такое CFR и IFR (чтобы люди не искали разницу между Италией и другими странами в уровне медицины), объяснить, что нельзя полагаться на оценки, полученные методом Deaths/Cases, а для любителей математики вроде меня еще и разобраться как этот метод можно исправить.
Летальность — это вероятность умереть, если у пациента диагностирована болезнь. Вот цитата из научной статьи:
one of the most important epidemiologic quantities to be determined is the case fatality ratio—the proportion of cases who eventually die from the disease.
Смертность — это отношение числа умерших от болезни к размеру популяции за какой-то промежуток времени. Обычно, считают сколько смертей на 100 тыс. населения за единицу времени. Смертность непосредственно связана с летальностью: это произведение вероятности заболеть (за определенный временной период) на летальность. В самом деле, для того, чтобы умереть от болезни надо сначала ей заразиться, а потом уж, если не повезет…
Высокая летальность не означает автоматически, что смертность тоже высокая. Например, болезнь убивает с вероятностью 1, но поражает всего 0.1% населения, скажем, за год (похожим образом ведет себя вирус Эболы, к примеру). Тогда смертность составит всего 1/1000. В то время как болезнь с летальностью в сто раз меньше (0.01) может иметь в 10 раз более высокую смертность (1/100), если поражает все население за тот же период.
Смертность явно зависит от времени — со временем количество инфицированных, как правило, увеличивается, поэтому и смертность растет. Летальность же от времени не зависит явным образом, но, например, может снизиться со временем, если найдут/изобретут лекарство.
Можно еще сказать, что летальность это условная вероятность смерти при условии болезни, а смертность — это вероятность умереть от болезни за какой-то временной промежуток.
Летальность, в свою очередь, подразделяется на Case Fatality Ratio (CFR) и Infection Fatality Ratio (IFR):
CFR — это летальность, рассчитанная по подтвержденным случаям. У этого показателя есть подводный камень: в первую очередь обычно тестируют тех, у кого ярко выражены симптомы. Поэтому можно сказать, что в первом приближении CFR — это вероятность смерти при условии наличия болезни и выраженных симптомов.
IFR — это и есть летальность, то есть вероятность смерти при наличии болезни. Этот показатель включает также легкие и бессимптомные случаи болезни и поэтому может быть намного меньше чем CFR. Точно рассчитать этот показатель практически невозможно, потому что мало кто станет тестировать все население, чтобы учесть и бессимптомных носителей тоже, но его можно оценить.
В эпидемиологии крайне важно уметь в начале эпидемии оценить летальность, чтобы иметь возможность принять меры, сообразные тяжести заболевания. К сожалению, сделать это чрезвычайно сложно и сейчас мы узнаем почему.
Одним из наиболее популярных методов оценки летальности является простая формула: Deaths / Cases, то есть количество смертей от болезни поделить на общее число инфицированных к текущему моменту. К сожалению, эта весьма популярная оценка (называемая также наивным методом) обладает врожденным недостатком, который иллюстрируется следующим примером:
Пусть некая болезнь убивает ровно за 1 месяц с вероятностью 1. Пусть также количество заболевших удваивается каждые 10 дней. Допустим, в первый месяц умерло х человек. Но заболевших, которые еще не умерли, в 7 раз больше! Просто потому, что за месяц произойдет три удвоения исходной популяции больных (а это увеличение в 8 раз). Поэтому метод, когда делят количество умерших на количество диагностированных оценит летальность всего лишь в%!
Эта недооценка наивного метода приводит к ложным спекуляциям. Например, во время эпидемии SARS наивная оценка росла со временем, порождая слухи о том, что вирус эволюционирует, превращаясь в более смертоносного убийцу. А причиной этого является простая математика: рост количества заболевших замедляется, что уменьшает недооценку летальности наивным эстиматором.
Таким образом, можно сказать, что наивный метод недооценивает летальность, уменьшая ее в
немножко совсем простенькой математики
Для начала давайте поймем сколько человек, которые заболели в первый день, умрут в n-ый день. Логика тут следующая: каждый день когорта заболевших в первый день уменьшается на величину  , где
, где  — это количество заболевших в первый день, а
— это количество заболевших в первый день, а  — это вероятность умереть в день j с момента заболевания. Иными словами
— это вероятность умереть в день j с момента заболевания. Иными словами  — это доля заболевших в первый день, которые умрут ровно в j-ый день с момента заболевания. Вспомним формулу условной вероятности:
— это доля заболевших в первый день, которые умрут ровно в j-ый день с момента заболевания. Вспомним формулу условной вероятности:  , где
, где  — это летальность (на самом деле, правильнее было записать
— это летальность (на самом деле, правильнее было записать  , но мы опустим это для краткости).
, но мы опустим это для краткости).
А теперь давайте посчитаем сколько же человек из заболевших в первый день умрет ко дню n:
Теперь посчитаем количество смертей для заболевших в другие дни (до дня n включительно) и сложим их:
Где (это следует из того, что количество кейсов растет по экспоненте). С учетом всего вышенаписанного:
(это следует из того, что количество кейсов растет по экспоненте). С учетом всего вышенаписанного:
Отсюда можно выразить bias-corrected летальность:
Таким образом, наивный эстиматор занижает реальную летальность в
занижает реальную летальность в  раз.
раз.
А теперь давайте посчитаем сколько же человек из заболевших в первый день умрет ко дню n:
Теперь посчитаем количество смертей для заболевших в другие дни (до дня n включительно) и сложим их:
Где
Отсюда можно выразить bias-corrected летальность:
Таким образом, наивный эстиматор
А теперь попробуем оценить этот bias для оценки летальности в ранний период развития эпидемии коронавирусной инфекции в китайском городе Ухань. Для этого воспользуемся следующими предположениями: время удвоения числа заболевших равно 5 дням, а среднее время от регистрации до смерти равно 18 дням.
обоснование предположений
Время удвоения количества зараженных (5 дней) и среднее время от появления симптомов до смерти (22.3 дня) были взяты отсюда
Но нам нужно среднее время не от появления симптомов, а от регистрации до смерти. Здесь было показано, что медианной время от появления симптомов до регистрации равняется 4.25 дням. Значит, среднее время от регистрации до смерти примерно равно 18 дням.
Но нам нужно среднее время не от появления симптомов, а от регистрации до смерти. Здесь было показано, что медианной время от появления симптомов до регистрации равняется 4.25 дням. Значит, среднее время от регистрации до смерти примерно равно 18 дням.
Еще предположим, что день смерти имеет распределение Пуассона:
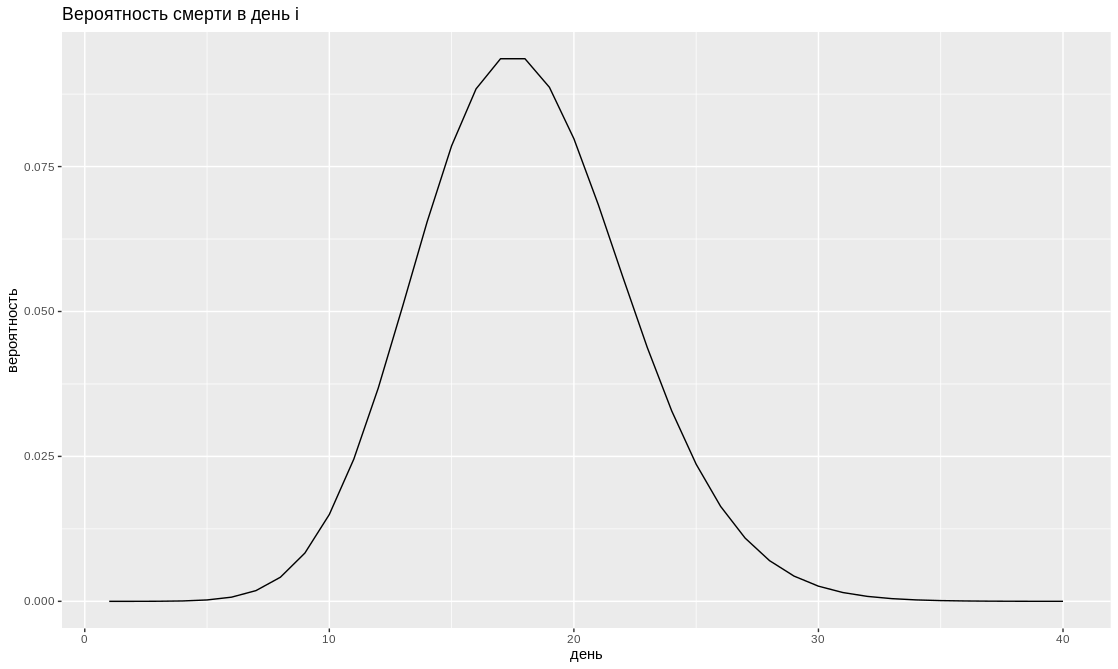
Подставив значения в формулу, получим, что наивный метод занижает летальность примерно в 9 раз. Таким образом, CFR по подтвержденным случаям составляет около 18%! Подчеркиваю, что CFR не включает недокументированных пациентов, количество которых оценили китайские ученые: по их модели, 86% случаев были не зарегистрированы. Это позволяет нам вычислить IFR: IFR = 0.14*CFR = 2.5%. Эти оценки прекрасно согласуются с оценками CFR (18%, 11%-81%), и IFR (1%, 0.5%-4%), которые были получены специалистами Imperial College London.
Важно понимать, что значение IFR не следует использовать для оценки вероятности умереть от болезни, так как вероятность умереть от болезни зависит от множества факторов:
- возраста
- наличия сопутствующих заболеваний
- загруженности больниц
- вирусной нагрузки
- и т. д.
Тогда для чего же так важно знать IFR хотя бы приблизительно? Это нужно знать для того, чтобы иметь возможность сравнить с известными заболеваниями. Например, летальность (IFR) гриппа составляет 0.01%, что, как минимум, в десятки раз ниже. С учетом того, факта, что коронавирус более заразный (R0 > 2 против примерно 1.3 у гриппа), это может привести к десяткам миллионов смертей по всему миру, так как грипп может уносить до 650 000 жизней в год. Поэтому ни в коем случае не стоит считать, что «это просто грипп».
Данная статья имеет следующие цели: объяснить в чем различие между смертность и летальностью, объяснить, что такое CFR и IFR (чтобы люди не искали разницу между Италией и другими странами в уровне медицины), объяснить, что нельзя полагаться на оценки, полученные методом Deaths/Cases, а для любителей математики вроде меня еще и разобраться как этот метод можно исправить.