Начало серии статей здесь

В этой части мы сосредоточимся на зеркальных отражениях, благодаря которым дюны напоминают океан песка.
Один из самых интригующих эффектов рендеринга песка Journey заключается в том, как дюны сверкают в лучах света. Такое отражение называется зеркальным (specular). Название произошло от латинского слова speculum, означающего «зеркало». Specular reflection — это «зонтичное» понятие, объединяющее в себе все типы взаимодействий, при которых свет сильно отражается в одном направлении, а не рассеивается и не поглощается. Именно благодаря зеркальным отражениям и вода, и отполированные поверхности под определённым углом выглядят сверкающими.
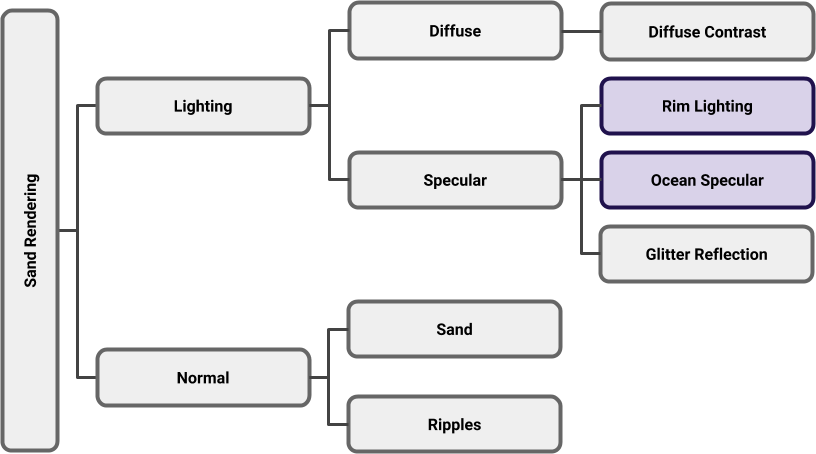
В Journey представлено три типа зеркальных отражений: свечение краёв (rim lighting), зеркальное отражение океана (ocean specular) и отражение отблесков (glitter reflections), показанные на схеме ниже. В этой части мы рассмотрим первые два типа.


До и после применения зеркальных отражений
Можно заметить, что на каждом уровне Journey представлен ограниченный набор цветов. И хотя это создаёт сильную и чистую эстетику, такой подход усложняет рендеринг песка. Дюны рендерятся только ограниченным количеством оттенков, поэтому игроку сложно понять, где на далёком расстоянии заканчивается одна и начинается другая.
Чтобы компенсировать это, край каждой дюны имеет небольшой эффект сияния, подсвечивающий её контуры. Это позволяет дюнам не скрываться в горизонт и создаёт иллюзию гораздо более обширного и сложного окружения.
Прежде чем начинать разбираться, как можно реализовать этот эффект, давайте расширим функцию освещения, добавив в неё diffuse colour (рассмотренный нами в предыдущей части статьи) и новый обобщённый компонент зеркального отражения.
В показанном выше фрагменте кода мы видим, что зеркальный компонент свечения краёв (rim lighting), который называется
Свечение краёв можно реализовать множеством разных способов. Наиболее популярный в кодировании шейдеров использует хорошо известную модель отражений по Френелю.
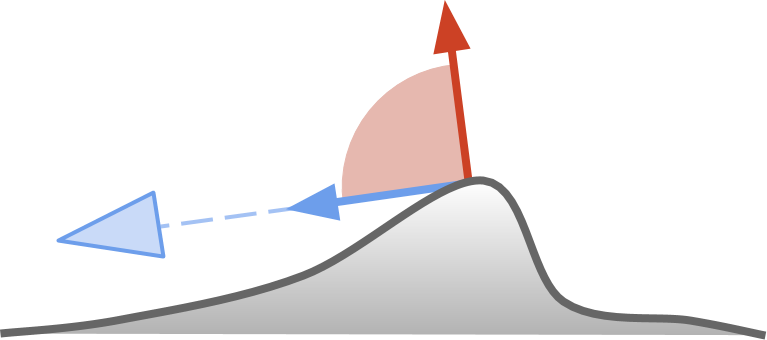
Чтобы понять уравнение, лежащее в основе отражения по Френелю, полезно визуализировать то, где оно происходит. На схеме ниже показано, как дюна видна через камеру (синим цветом). Красной стрелкой обозначена нормаль поверхности вершины дюны, где и должно быть зеркальное отражение. Легко заметить, что все края дюны имеют общее свойство: их нормаль ( , красного цвета) перпендикулярна направлению взгляда (
, красного цвета) перпендикулярна направлению взгляда ( , синего цвета).
, синего цвета).
Аналогично тому, что мы сделали в части про Diffuse Colour, можно использовать скалярное произведение и
и  , чтобы получить меру их параллельности. В данном случае
, чтобы получить меру их параллельности. В данном случае  равняется
равняется  , ведь два единичных вектора перпендикулярны; вместо этого мы можем использовать
, ведь два единичных вектора перпендикулярны; вместо этого мы можем использовать  для получения меры их непараллельности.
для получения меры их непараллельности.
Непосредственное использование не даст нам хороших результатов, потому что отражение будет слишком сильным. Если мы хотим сделать отражение резче, то можем просто взять выражение в степени. Степень величины от
не даст нам хороших результатов, потому что отражение будет слишком сильным. Если мы хотим сделать отражение резче, то можем просто взять выражение в степени. Степень величины от  до
до  остаётся ограниченной одним интервалом, но переход между темнотой и светом становится резче.
остаётся ограниченной одним интервалом, но переход между темнотой и светом становится резче.
В модели отражений по Френелю заявляется, что яркость света задаётся следующим образом:
задаётся следующим образом:
где и
и  — это два параметра, которые можно использовать для управления контрастностью и силой эффекта. Параметры
— это два параметра, которые можно использовать для управления контрастностью и силой эффекта. Параметры  и
и  иногда называют specular и gloss, однако названия могут и меняться.
иногда называют specular и gloss, однако названия могут и меняться.
Уравнение (1) очень легко преобразовать в код:
Его результат показан на анимации ниже.
Одним самых оригинальных аспектов геймплея Journey стало то, что иногда игрок в буквальном смысле может «сёрфить» по дюнам. Ведущий инженер Джон Эдвардс объяснил, что thatgamecompany стремилась, чтобы песок больше ощущался не твёрдым, а жидким.
И это не совсем ошибочно, ведь песок можно воспринимать как очень грубую аппроксимацию жидкости. А в определённых условиях, например, в песочных часах, он даже ведёт себя подобно жидкости.
Чтобы подкрепить идею о том, что песок может иметь компонент жидкости, в Journey был добавлен второй эффект отражения, который часто встречается в жидких телах. Джон Эдвардс называет его ocean specular (зеркальным отражением океана): идея заключается в том, чтобы получить тот же тип отражений, который виден на поверхности океана или озера на закате солнца (см. ниже).

Как и прежде, внесём изменения в функцию освещения
Зеркальные отражения на воде часто реализуются при помощи отражения по Блинну-Фонгу, являющегося малозатратным решением для блестящих материалов. Впервые оно было описано Джеймсом Ф. Блинном в 1977 году (статья: "Models of Light Reflection for Computer Synthesized Pictures") как аппроксимация более ранней техники затенения, разработанной Буй Тыонг Фонгом в 1973 году (статья: "Illumination for Computer Generated Pictures").
При использовании затенения по Блинну-Фонгу светимость (luminosity) поверхности задаётся следующим уравнением:
поверхности задаётся следующим уравнением:
где
Знаменатель уравнения (3) делит вектор на его длину. Это гарантирует, что
на его длину. Это гарантирует, что  имеет длину
имеет длину  . Эквивалентная шейдерная функция для выполнения этой операции — это
. Эквивалентная шейдерная функция для выполнения этой операции — это  представляет вектор «между»
представляет вектор «между»  и
и  , и поэтому называется полувектором (half vector).
, и поэтому называется полувектором (half vector).

Более подробное описание отражения по Блинну-Фонгу можно найти в туториале Physically Based Rendering and Lighting Models. Ниже представлено его простая реализация в коде шейдера.
В анимации представлено сравнение традиционого диффузного затенения по Ламберту и зеркального по Блинну-Фонгу:
В этой части мы воссоздадим блестящие отражения, которые обычно видны на песчаных дюнах.
Вскоре после публикации моей серии статей Джулиан Обербек и Пол Нэделек предприняли собственную попытку воссоздания в Unity сцены, вдохновлённой игрой Journey. В твите ниже видно как они усовершенствовали блестящие отражения, чтобы обеспечить бОльшую временную целостность. Подробнее об их реализации можно прочитать в статье на IndieBurg Mip Map Folding.
В предыдущей части курса мы раскрыли реализацию двух функций зеркальных отражений в рендеринге песка Journey: rim lighting и ocean specular. В этой части я объясню, как реализовать последний вариант зеркального отражения: блеск (glitter).

Если вы когда-нибудь бывали в пустыни, то наверняка замечали, насколько песок на самом деле блестящий. Как говорилось в части о нормалях песка, каждая песчинка потенциально может отражать свет в случайном направлении. Благодаря самой природе случайных чисел часть этих отражённых лучей попадёт в камеру. Из-за этого случайные точки песка будут казаться очень яркими. Этот блеск очень чувствителен к движению, так как малейший сдвиг помешает отражённым лучам попадать в камеру.
В других играх, например, в Astroneer и Slime Rancher блестящие отражения использовались для песка и пещер.


Блеск: до и после наложения эффекта
Проще оценить эти характеристики блеска в увеличенном изображении:

Без всяких сомнений, эффект блеска на реальных дюнах полностью зависит от того, что некоторые песчинки случайным образом отражают свет нам в глаза. Строго говоря, именно это мы уже смоделировали во второй части курса, посвящённой нормалям песка, когда мы моделировали случайное распределение нормалей. Так зачем же нам нужен для этого ещё один эффект?
Ответ может быть не слишком очевиден. Давайте представим, что мы пытаемся воссоздать эффект блеска только при помощи нормалей. Даже если все нормали будут направлены в камеру, песок всё равно не будет блестеть, потому что нормали могут отражать только ту величину света, которая доступна в сцене. То есть в лучшем случае мы отразим только 100% света (если песок совершенно белый).
Но нам нужно нечто другое. Если мы хотим, чтобы пиксель казался таким ярким, чтобы свет растекался на соседние с ним пиксели, то цвет должен быть больше . Так получилось потому, что в Unity при применении к камере фильтра bloom при помощи эффекта постобработки, цвета ярче
. Так получилось потому, что в Unity при применении к камере фильтра bloom при помощи эффекта постобработки, цвета ярче  распространяются на соседние пиксели и приводят к появлению гало, создающего ощущение того, что некоторые пиксели светятся. Это фундамент HDR-рендеринга.
распространяются на соседние пиксели и приводят к появлению гало, создающего ощущение того, что некоторые пиксели светятся. Это фундамент HDR-рендеринга.
Так что нет, наложение нормалей невозможно простым образом использовать для создания блестящих поверхностей. Поэтому такой эффект удобнее реализовать как отдельный процесс.
Чтобы подойти к ситуации более формально, нам нужно воспринимать дюны как состоящие из микроскопических зеркал, каждое из которых имеет случайное направление. Такой подход называется теорией микрограней (microfacet theory), где микрогранью (microfacet) называется каждое из этих крошечных зеркал. Математический фундамент большинства современных моделей затенения основан на теории микрограней, в том числе и модели Standard shader из Unity.
Первым шагом будет разделение поверхности дюны на микрограни и определение ориентации каждой из них. Как уже говорилось, мы делали нечто подобное в части туториала, посвящённой нормалям песка, где UV-позиция 3D-модели дюны использовалась для сэмплирования случайной текстуры. Тот же подход можно использовать и здесь, чтобы привязать к каждой микрограни случайную ориентацию. Размер каждой микрограни будет зависеть от масштаба тектуры и от её уровня mip-текстурирования. Наша задача заключается в воссоздании определённой эстетики, а не стремлении к фотореализму; такой подход будет достаточно хорош для нас.
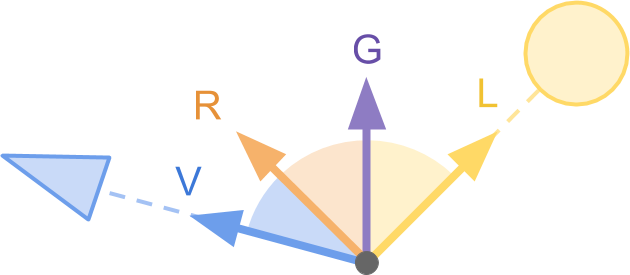
После сэмплирования случайной текстуры мы сможем связать с каждой песчинкой/микрогранью дюны случайное направление. Давайте назовём его . Оно обозначает направление блеска, то есть направление нормали песчинки, на которую мы смотрим. Луч света, падающий на песчинку, будет отражаться с учётом того, что микрогрань — это идеальное зеркало, ориентированное в направлении
. Оно обозначает направление блеска, то есть направление нормали песчинки, на которую мы смотрим. Луч света, падающий на песчинку, будет отражаться с учётом того, что микрогрань — это идеальное зеркало, ориентированное в направлении  . В камеру должен попасть получившийся отражённый луч света
. В камеру должен попасть получившийся отражённый луч света  (см. ниже).
(см. ниже).
Здесь мы снова можем использовать скалярное произведение и
и  для получения меры их параллельности.
для получения меры их параллельности.
Один из подходов заключается в возведении в степень , как объяснено в предыдущей (четвёртой) части статьи. Если попробовать так сделать, то мы увидим, что результат очень отличается от того, что есть в Journey. Блестящие отражения должны быть редкими и очень яркими. Проще всего будет учитывать только те блестящие отражения, для которых
, как объяснено в предыдущей (четвёртой) части статьи. Если попробовать так сделать, то мы увидим, что результат очень отличается от того, что есть в Journey. Блестящие отражения должны быть редкими и очень яркими. Проще всего будет учитывать только те блестящие отражения, для которых  находится ниже определённого порогового значения.
находится ниже определённого порогового значения.
Мы можем с лёгкостью реализовать описанный выше эффект блеска при помощи функции .
.
Строго говоря, если совершенно случайно, то
совершенно случайно, то  тоже будет совершенно случайным. Может показаться, что использовать
тоже будет совершенно случайным. Может показаться, что использовать
Результаты показаны ниже:
Как мы помним из самой первой части туториала, компонент блеска добавляется к окончательному цвету.
Существует большая вероятность того, что некоторые пиксели в конечном итоге получат цвет больше , что приведёт к эффекту bloom. Именно это нам и нужно. Эффект также добавляется поверх уже существующего зеркального отражения (рассмотренного в предыдущей части статьи), поэтому блестящие песчинки могут находиться даже там, где дюны хорошо освещены.
, что приведёт к эффекту bloom. Именно это нам и нужно. Эффект также добавляется поверх уже существующего зеркального отражения (рассмотренного в предыдущей части статьи), поэтому блестящие песчинки могут находиться даже там, где дюны хорошо освещены.
Существует множество способов усовершенствования этой техники. Всё зависит от итога, которого вы хотите достичь. В Astroneer и Slime Rancher, например, этот эффект используется только ночью. Этого можно добиться снижением силы эффекта блеска в зависимости от направления солнечного света.
Например, величина , когда солнце падает сверху, и равна нулю, когда оно за горизонтом. Но вы можете создать собственную систему, внешний вид которой зависит от ваших предпочтений.
, когда солнце падает сверху, и равна нулю, когда оно за горизонтом. Но вы можете создать собственную систему, внешний вид которой зависит от ваших предпочтений.
В последней части статьи мы воссоздадим типичные волны песка, возникающие вследствие взаимодействия дюн и ветра.



Волны на поверхности дюн: до и после
Теоретически логично эту часть было бы поставить после части о нормалях песка. Я оставил её напоследок потому, что это самый сложный из эффектов туториала. Частично эта сложность вызвана тем, как хранятся и обрабатываются карты нормалей поверхностным шейдером, выполняющим множество дополнительных шагов.
В предыдущей (пятой) части мы исследовали способ получения неоднородного песка. В части, посвящённой нормалям песка для изменения способа взаимодействия света с поверхностью геометрии была использовала очень популярная техника наложения карт нормалей (normal mapping). Она часто применяется в 3D-графике для создания иллюзии того, что объект имеет более сложную геометрию, и обычно используется, чтобы сделать кривые поверхности более плавными (см. ниже).
Чтобы достичь такого эффекта, каждый пиксель сопоставляется с направлением нормали, обозначающим его ориентацию. И оно используется для вычисления освещения вместо истинной ориентации меша.
Считывая направления нормалей из кажущейся случайной текстуры, мы смогли имитировать зернистость. Несмотря на физическую неточность, она всё равно выглядит правдоподобно.
Однако песчаные дюны демонстрируют и другую особенность, которую невозможно игнорировать: волны. На каждой дюне есть дюны поменьше, появляющиеся из-за воздействия ветра и удерживаемые вместе трением отдельных песчинок.
Эти волны очень заметны и видны на большинстве дюн. На показанной ниже фотографии, сделанной в Омане, видно, что ближняя часть дюны имеет выраженный волнистый узор.

Эти волны значительно изменяются в зависимости не только от формы дюны, но и от состава, направления и скорости ветра. У большинства дюн с острым пиком волны присутствуют только с одной стороны (см. ниже).

Представленный в туториале эффект рассчитан на более плавные дюны, имеющие волны по обеим сторонам. Это не всегда физически точно, но достаточно реалистично для того, чтобы быть правдоподобным, и является хорошим первым шагом к более сложным реализациям.
Существует множество способов реализации волн. Наименее затратным будет простое рисование их на текстуре, но в туториале мы хотим достичь иного. Причина проста: волны не «плоские» и должны правильно взаимодействовать со светом. Если просто нарисовать их, то невозможно будет добиться реалистичного эффекта при движении камеры (или солнца).
Ещё одним способом добавления волн является изменение геометрии модели дюны. Но повышать сложность модели не рекомендуется, потому что это сильно влияет на общую производительность.
Как мы видели в части про нормали песка, обойти эту проблему можно при помощи карт нормалей. По сути, они отрисовываются на поверхности как традиционные текстуры, но используются в вычислении освещения для имитации более сложной геометрии.
То есть задача превратилась в другую: как создать эти карты нормалей. Ручная отрисовка будет слишком затратной по времени. Кроме того, при каждом изменении дюны нужно будет перерисовывать волны заново. Это значительно замедлит процесс создания ресурсов, чего стремятся избегать многие технические художники.
Гораздо более эффективным и оптимальным решением будет добавление волн процедурным образом. Это значит, что направления нормалей дюны изменяются на основании локальной геометрии, чтобы учесть не только песчинки, но и волны.
Так как волны нужно имитировать на 3D-поверхности, будет логичнее реализовать изменение направления нормалей для каждого пикселя. Для этого проще использовать бесшовную карту нормалей с волновым паттерном. Затем эта карта будет скомбинирована с уже имеющейся картой нормалей, ранее использованной для песка.
До этого момента мы встречались с тремя разными нормалями:
На примере ниже, взятом со страницы Unity Surface Shader examples, демонстрируется стандартный способ перезаписи нормали 3D-модели. Для этого требуется изменить значение
Точно такую же технику мы использовали для замены нормали геометрии нормалью песка.
Однако первая сложность связана с тем, что форма волн изменяется в зависимости остроты дюн. Невысокие, плоские дюны имеют небольшие волны; на крутых дюнах волновые паттерны более отчётливы. Это значит, что нужно учитывать крутизну дюны.
Проще всего обойти эту проблему, создав две разные карты нормалей, соответственно для плоских и крутых дюн. Основная идея заключается в том, чтобы выполнять смешение между этими двумя картами нормалей на основании крутизны дюны.

Карта нормалей для крутой дюны

Карта нормалей для плоской дюны
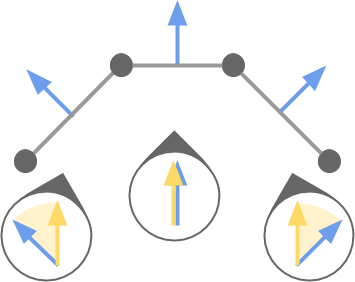
Крутизну можно вычислить при помощи скалярного произведения, которое часто применяется в кодировании шейдеров для вычисления степени «параллельности» двух направлений. В данном случае мы берём направление нормали геометрии (ниже показана синим) и сравниваем её с вектором, указывающим в небо (ниже показан жёлтым). Скалярное произведение этих двух векторов возвращает значения, близкие к , когда векторы почти параллельны (плоские дюны), и близкие к
, когда векторы почти параллельны (плоские дюны), и близкие к  , когда между ними угол 90 градусов (крутые дюны).
, когда между ними угол 90 градусов (крутые дюны).
Однако мы сталкиваемся с первой проблемой — в этой операции участвует два вектора. Вектор нормали, получаемый из функции

Вектор же, указывающий в небо, выражен в мировом пространстве. Чтобы получить правильное скалярное произведение, оба вектора нужно выразить в одной системе координат. Это означает, что нам нужно преобразовать один из них, чтобы оба были выражены в одном пространстве.
К счастью, нам на помощь приходит Unity с функцией
Это объясняется в статье из документации Unity Writing Surface Shaders, где говорится:
Часто это становится основным источником проблем при написании поверхностных шейдеров. По сути, значение
Если вы выполняете запись в
Фрагмент представленного ниже кода преобразует нормаль из касательного в мировое пространство и вычисляет крутизну относительно направления «вверх».
Теперь, когда мы вычислили крутизну дюны, можно использовать её для смешения двух карт нормалей. Сэмплируются обе карты нормалей, и плоская, и крутая (в коде ниже они называются
Как говорилось в части о нормалях песка, правильно комбинировать карты нормалей довольно сложно, и это невозможно сделать при помощи
Если мы используем показанный выше код, то результаты могут нас разочаровать. Так происходит потому, что дюны имеют очень небольшую крутизну, что приводит к слишком сильному смешиванию двух текстур нормалей. Чтобы исправить это, мы можем применить к крутизне нелинейное преобразование, что повысит резкость смешения:
При смешении двух текстур для регулирования их резкости и контрастности часто используется
Ниже мы видим два градиента. На верхнем представлены цвета от чёрного к белому, линейно интерполированные по оси X с помощью


Легко заметить, что
Всё, что мы сделали ранее, работает идеально. Но нам нужно решить ещё одну последнюю проблему. Волны изменяются в зависимости от крутизны, но не от направления. Как говорилось выше, волны обычно не бывают симметричными из-за того, что ветер преимущественно дует в одном направлении.
Чтобы сделать волны ещё реалистичнее, нам нужно добавить ещё две карты нормалей (см. таблицу ниже). Их можно смешивать в зависимости от параллельности дюны оси X или оси Z.
Здесь нам нужно реализовать вычисление параллельности дюны относительно оси Z. Это можно сделать аналогично вычислению крутизны, но вместо
Этот последний шаг я оставлю вам. Если у вас возникнут проблемы, то в конце этого туториала есть ссылка на скачивание полного пакета Unity.
Это последняя часть серии туториалов о рендеринге песка игры Journey.
Ниже показано, как далеко мы смогли продвинуться в этой серии:


До и после
Хочу поблагодарить вас за то, что дочитали до конца этот довольно длинный туториал. Надеюсь, вам понравилось изучать и воссоздавать этот шейдер.
Видеоигра Journey была разработана Thatgamecompany и издана Sony Computer Entertainment. Она доступна для PC (Epic Store) и PS4 (PS Store).
3D-модели дюн, фоны и параметры освещения были созданы Jiadi Deng.
3D-модель персонажа Journey найдена на форуме FacePunch (ныне закрытом).
Если вы хотите воссоздать этот эффект, то полный пакет Unity доступен для скачивания на Patreon. В нём есть всё необходимое, от шейдеров до 3D-моделей.

Часть 4: зеркальное отражение
В этой части мы сосредоточимся на зеркальных отражениях, благодаря которым дюны напоминают океан песка.
Один из самых интригующих эффектов рендеринга песка Journey заключается в том, как дюны сверкают в лучах света. Такое отражение называется зеркальным (specular). Название произошло от латинского слова speculum, означающего «зеркало». Specular reflection — это «зонтичное» понятие, объединяющее в себе все типы взаимодействий, при которых свет сильно отражается в одном направлении, а не рассеивается и не поглощается. Именно благодаря зеркальным отражениям и вода, и отполированные поверхности под определённым углом выглядят сверкающими.
В Journey представлено три типа зеркальных отражений: свечение краёв (rim lighting), зеркальное отражение океана (ocean specular) и отражение отблесков (glitter reflections), показанные на схеме ниже. В этой части мы рассмотрим первые два типа.



До и после применения зеркальных отражений
Rim Lighting
Можно заметить, что на каждом уровне Journey представлен ограниченный набор цветов. И хотя это создаёт сильную и чистую эстетику, такой подход усложняет рендеринг песка. Дюны рендерятся только ограниченным количеством оттенков, поэтому игроку сложно понять, где на далёком расстоянии заканчивается одна и начинается другая.
Чтобы компенсировать это, край каждой дюны имеет небольшой эффект сияния, подсвечивающий её контуры. Это позволяет дюнам не скрываться в горизонт и создаёт иллюзию гораздо более обширного и сложного окружения.
Прежде чем начинать разбираться, как можно реализовать этот эффект, давайте расширим функцию освещения, добавив в неё diffuse colour (рассмотренный нами в предыдущей части статьи) и новый обобщённый компонент зеркального отражения.
float4 LightingJourney (SurfaceOutput s, fixed3 viewDir, UnityGI gi)
{
// Lighting properties
float3 L = gi.light.dir;
float3 N = s.Normal;
// Lighting calculation
float3 diffuseColor = DiffuseColor (N, L);
float3 rimColor = RimLighting (N, V);
// Combining
float3 color = diffuseColor + rimColor;
// Final color
return float4(color * s.Albedo, 1);
}В показанном выше фрагменте кода мы видим, что зеркальный компонент свечения краёв (rim lighting), который называется
rimColor, просто прибавляется к исходному diffuse colour.
Эффекты High Dynamic Range и Bloom
И диффузный компонент, и свечение краёв — это цвета RGB в интервале от  до
до  . Окончательный цвет определяется их суммой. Это означает, что он потенциально может оказаться больше
. Окончательный цвет определяется их суммой. Это означает, что он потенциально может оказаться больше  .
.
Если вы не новичок в кодировании шейдеров, то можете знать, что цвета должны быть ограничены интервалом от до
до  . Однако существуют случаи, когда нам нужно, чтобы цвета превышали
. Однако существуют случаи, когда нам нужно, чтобы цвета превышали  . Если у камеры включена поддержка High Dynamic Range, то пиксели с яркостью выше
. Если у камеры включена поддержка High Dynamic Range, то пиксели с яркостью выше  будут «пропускать» свет на ближайшие пиксели. Эта техника используется для имитации эффектов bloom, гало и зеркальных засветов. Однако для выполнения этой операции требуется эффект постобработки.
будут «пропускать» свет на ближайшие пиксели. Эта техника используется для имитации эффектов bloom, гало и зеркальных засветов. Однако для выполнения этой операции требуется эффект постобработки.
Если вы не новичок в кодировании шейдеров, то можете знать, что цвета должны быть ограничены интервалом от
Отражения по Френелю
Свечение краёв можно реализовать множеством разных способов. Наиболее популярный в кодировании шейдеров использует хорошо известную модель отражений по Френелю.
Чтобы понять уравнение, лежащее в основе отражения по Френелю, полезно визуализировать то, где оно происходит. На схеме ниже показано, как дюна видна через камеру (синим цветом). Красной стрелкой обозначена нормаль поверхности вершины дюны, где и должно быть зеркальное отражение. Легко заметить, что все края дюны имеют общее свойство: их нормаль (

Аналогично тому, что мы сделали в части про Diffuse Colour, можно использовать скалярное произведение
Непосредственное использование
В модели отражений по Френелю заявляется, что яркость света
где
Уравнение (1) очень легко преобразовать в код:
float _TerrainRimPower;
float _TerrainRimStrength;
float3 _TerrainRimColor;
float3 RimLighting(float3 N, float3 V)
{
float rim = 1.0 - saturate(dot(N, V));
rim = saturate(pow(rim, _TerrainRimPower) * _TerrainRimStrength);
rim = max(rim, 0); // Never negative
return rim * _TerrainRimColor;
}Его результат показан на анимации ниже.
Ocean Specular
Одним самых оригинальных аспектов геймплея Journey стало то, что иногда игрок в буквальном смысле может «сёрфить» по дюнам. Ведущий инженер Джон Эдвардс объяснил, что thatgamecompany стремилась, чтобы песок больше ощущался не твёрдым, а жидким.
И это не совсем ошибочно, ведь песок можно воспринимать как очень грубую аппроксимацию жидкости. А в определённых условиях, например, в песочных часах, он даже ведёт себя подобно жидкости.
Чтобы подкрепить идею о том, что песок может иметь компонент жидкости, в Journey был добавлен второй эффект отражения, который часто встречается в жидких телах. Джон Эдвардс называет его ocean specular (зеркальным отражением океана): идея заключается в том, чтобы получить тот же тип отражений, который виден на поверхности океана или озера на закате солнца (см. ниже).

Как и прежде, внесём изменения в функцию освещения
LightingJourney, чтобы добавить в неё новый тип зеркального отражения.float4 LightingJourney (SurfaceOutput s, fixed3 viewDir, UnityGI gi)
{
// Lighting properties
float3 L = gi.light.dir;
float3 N = s.Normal;
float3 V = viewDir;
// Lighting calculation
float3 diffuseColor = DiffuseColor (N, L);
float3 rimColor = RimLighting (N, V);
float3 oceanColor = OceanSpecular (N, L, V);
// Combining
float3 specularColor = saturate(max(rimColor, oceanColor));
float3 color = diffuseColor + specularColor;
// Final color
return float4(color * s.Albedo, 1);
}
Почему мы берём максимум от двух компонентов отражения?
Есть большая вероятность того, что возникнет наложение rim lighting и ocean specular. Некоторые части дюны, особенно расположенные под углами скольжения, могут одновременно демонстрировать отражения по Френелю и по Блинну-Фонугу. Если их суммировать, то дюна будет слишком блестеть.
Мы берём максимум из них, и это эффективный способ избежать такой проблемы.
Мы берём максимум из них, и это эффективный способ избежать такой проблемы.
Зеркальные отражения на воде часто реализуются при помощи отражения по Блинну-Фонгу, являющегося малозатратным решением для блестящих материалов. Впервые оно было описано Джеймсом Ф. Блинном в 1977 году (статья: "Models of Light Reflection for Computer Synthesized Pictures") как аппроксимация более ранней техники затенения, разработанной Буй Тыонг Фонгом в 1973 году (статья: "Illumination for Computer Generated Pictures").
При использовании затенения по Блинну-Фонгу светимость (luminosity)
где
Знаменатель уравнения (3) делит вектор
normalize. С геометрической точки зрения, 
Почему H находится между V и L?
Возможно, не совсем понятно, почему  — вектор между
— вектор между  и
и  .
.
Чтобы разобраться давайте вспомним тождество параллелограмма, дающее геометрическую интерпретацию суммы между двумя векторами. Сумму и
и  можно найти переносом
можно найти переносом  в конец
в конец  и проведением нового вектора от начала
и проведением нового вектора от начала  к концу
к концу  .
.
Следующим шагом к пониманию станет то, что две величины, и
и  , одинаковы. Это значит, что одинаковы два следующих геометрических построения:
, одинаковы. Это значит, что одинаковы два следующих геометрических построения:

Мы можем объединить их, образовав параллелограмм, стороны которого имеют одинаковую длину. Благодаря этому можно гарантировать, что диагональ (то есть ) делит угол пополам. Это значит, что синий и жёлтый углы равны (внизу слева).
) делит угол пополам. Это значит, что синий и жёлтый углы равны (внизу слева).
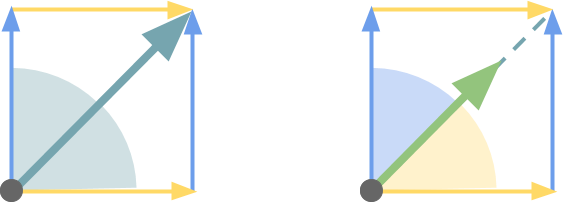
Теперь мы знаем, что — это вектор между
— это вектор между  и
и  , но его длина необязательно должна равняться
, но его длина необязательно должна равняться  . Нормализация обозначает растягивание его, пока он не достигнет длины
. Нормализация обозначает растягивание его, пока он не достигнет длины  , что превратит его в единичный вектор (вверху справа).
, что превратит его в единичный вектор (вверху справа).
Чтобы разобраться давайте вспомним тождество параллелограмма, дающее геометрическую интерпретацию суммы между двумя векторами. Сумму
Следующим шагом к пониманию станет то, что две величины,

Мы можем объединить их, образовав параллелограмм, стороны которого имеют одинаковую длину. Благодаря этому можно гарантировать, что диагональ (то есть

Теперь мы знаем, что
Более подробное описание отражения по Блинну-Фонгу можно найти в туториале Physically Based Rendering and Lighting Models. Ниже представлено его простая реализация в коде шейдера.
float _OceanSpecularPower;
float _OceanSpecularStrength;
float3 _OceanSpecularColor;
float3 OceanSpecular (float3 N, float3 L, float3 V)
{
// Blinn-Phong
float3 H = normalize(V + L); // Half direction
float NdotH = max(0, dot(N, H));
float specular = pow(NdotH, _OceanSpecularPower) * _OceanSpecularStrength;
return specular * _OceanSpecularColor;
}В анимации представлено сравнение традиционого диффузного затенения по Ламберту и зеркального по Блинну-Фонгу:
Часть 5: блестящее отражение
В этой части мы воссоздадим блестящие отражения, которые обычно видны на песчаных дюнах.
Вскоре после публикации моей серии статей Джулиан Обербек и Пол Нэделек предприняли собственную попытку воссоздания в Unity сцены, вдохновлённой игрой Journey. В твите ниже видно как они усовершенствовали блестящие отражения, чтобы обеспечить бОльшую временную целостность. Подробнее об их реализации можно прочитать в статье на IndieBurg Mip Map Folding.
В предыдущей части курса мы раскрыли реализацию двух функций зеркальных отражений в рендеринге песка Journey: rim lighting и ocean specular. В этой части я объясню, как реализовать последний вариант зеркального отражения: блеск (glitter).

Если вы когда-нибудь бывали в пустыни, то наверняка замечали, насколько песок на самом деле блестящий. Как говорилось в части о нормалях песка, каждая песчинка потенциально может отражать свет в случайном направлении. Благодаря самой природе случайных чисел часть этих отражённых лучей попадёт в камеру. Из-за этого случайные точки песка будут казаться очень яркими. Этот блеск очень чувствителен к движению, так как малейший сдвиг помешает отражённым лучам попадать в камеру.
В других играх, например, в Astroneer и Slime Rancher блестящие отражения использовались для песка и пещер.


Блеск: до и после наложения эффекта
Проще оценить эти характеристики блеска в увеличенном изображении:


Без всяких сомнений, эффект блеска на реальных дюнах полностью зависит от того, что некоторые песчинки случайным образом отражают свет нам в глаза. Строго говоря, именно это мы уже смоделировали во второй части курса, посвящённой нормалям песка, когда мы моделировали случайное распределение нормалей. Так зачем же нам нужен для этого ещё один эффект?
Ответ может быть не слишком очевиден. Давайте представим, что мы пытаемся воссоздать эффект блеска только при помощи нормалей. Даже если все нормали будут направлены в камеру, песок всё равно не будет блестеть, потому что нормали могут отражать только ту величину света, которая доступна в сцене. То есть в лучшем случае мы отразим только 100% света (если песок совершенно белый).
Но нам нужно нечто другое. Если мы хотим, чтобы пиксель казался таким ярким, чтобы свет растекался на соседние с ним пиксели, то цвет должен быть больше
Так что нет, наложение нормалей невозможно простым образом использовать для создания блестящих поверхностей. Поэтому такой эффект удобнее реализовать как отдельный процесс.
Теория микрограней
Чтобы подойти к ситуации более формально, нам нужно воспринимать дюны как состоящие из микроскопических зеркал, каждое из которых имеет случайное направление. Такой подход называется теорией микрограней (microfacet theory), где микрогранью (microfacet) называется каждое из этих крошечных зеркал. Математический фундамент большинства современных моделей затенения основан на теории микрограней, в том числе и модели Standard shader из Unity.
Первым шагом будет разделение поверхности дюны на микрограни и определение ориентации каждой из них. Как уже говорилось, мы делали нечто подобное в части туториала, посвящённой нормалям песка, где UV-позиция 3D-модели дюны использовалась для сэмплирования случайной текстуры. Тот же подход можно использовать и здесь, чтобы привязать к каждой микрограни случайную ориентацию. Размер каждой микрограни будет зависеть от масштаба тектуры и от её уровня mip-текстурирования. Наша задача заключается в воссоздании определённой эстетики, а не стремлении к фотореализму; такой подход будет достаточно хорош для нас.
После сэмплирования случайной текстуры мы сможем связать с каждой песчинкой/микрогранью дюны случайное направление. Давайте назовём его

Здесь мы снова можем использовать скалярное произведение
Один из подходов заключается в возведении в степень
Реализация
Мы можем с лёгкостью реализовать описанный выше эффект блеска при помощи функции
reflect в Cg, которая позволяет очень просто вычислять sampler2D_float _GlitterTex;
float _GlitterThreshold;
float3 _GlitterColor;
float3 GlitterSpecular (float2 uv, float3 N, float3 L, float3 V)
{
// Random glitter direction
float3 G = normalize(tex2D(_GlitterTex, uv).rgb * 2 - 1); // [0,1]->[-1,+1]
// Light that reflects on the glitter and hits the eye
float3 R = reflect(L, G);
float RdotV = max(0, dot(R, V));
// Only the strong ones (= small RdotV)
if (RdotV > _GlitterThreshold)
return 0;
return (1 - RdotV) * _GlitterColor;
}Строго говоря, если
reflect необязательно. И хотя это верно для статического кадра, но что произойдёт, если источник освещения перемещается? Это может быть или из-за движения самого солнца, или из-за точечного источника света, привязанного к игроку. В обоих случаях песок потеряет временнУю целостность между текущим и последующим кадром, из-за чего эффект блеска будет появляться в случайных местах. Однако использование функции reflect обеспечивает гораздо более стабильный рендеринг.Результаты показаны ниже:
Как мы помним из самой первой части туториала, компонент блеска добавляется к окончательному цвету.
#pragma surface surf Journey fullforwardshadows
float4 LightingJourney (SurfaceOutput s, fixed3 viewDir, UnityGI gi)
{
float3 diffuseColor = DiffuseColor ();
float3 rimColor = RimLighting ();
float3 oceanColor = OceanSpecular ();
float3 glitterColor = GlitterSpecular ();
float3 specularColor = saturate(max(rimColor, oceanColor));
float3 color = diffuseColor + specularColor + glitterColor;
return float4(color * s.Albedo, 1);
}Существует большая вероятность того, что некоторые пиксели в конечном итоге получат цвет больше
Существует множество способов усовершенствования этой техники. Всё зависит от итога, которого вы хотите достичь. В Astroneer и Slime Rancher, например, этот эффект используется только ночью. Этого можно добиться снижением силы эффекта блеска в зависимости от направления солнечного света.
Например, величина
max(dot(L, fixed3(0,1,0),0)) равна
Почему в отражении по Блинну-Фонгу не используется reflect?
Эффект ocean specular, рассмотренный нами в предыдущей части, был реализован с помощью отражения по Блинну-Фонгу.
Это очень популярная модель, которая использовалась на ранних этапах развития 3D-графики для затенения поверхностью с высокой отражаемостью, например, металла и пластика. Но проблема в том, что функция на
на  , что является очень близкой аппроксимацией.
, что является очень близкой аппроксимацией.
Это очень популярная модель, которая использовалась на ранних этапах развития 3D-графики для затенения поверхностью с высокой отражаемостью, например, металла и пластика. Но проблема в том, что функция
reflect может быть затратной. Для направленных вперёд поверхностей отражения по Блинну-Фонгу заменяютЧасть 6: волны
В последней части статьи мы воссоздадим типичные волны песка, возникающие вследствие взаимодействия дюн и ветра.



Волны на поверхности дюн: до и после
Теоретически логично эту часть было бы поставить после части о нормалях песка. Я оставил её напоследок потому, что это самый сложный из эффектов туториала. Частично эта сложность вызвана тем, как хранятся и обрабатываются карты нормалей поверхностным шейдером, выполняющим множество дополнительных шагов.
Карты нормалей
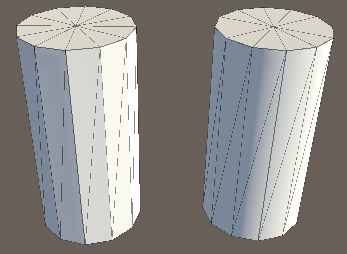
В предыдущей (пятой) части мы исследовали способ получения неоднородного песка. В части, посвящённой нормалям песка для изменения способа взаимодействия света с поверхностью геометрии была использовала очень популярная техника наложения карт нормалей (normal mapping). Она часто применяется в 3D-графике для создания иллюзии того, что объект имеет более сложную геометрию, и обычно используется, чтобы сделать кривые поверхности более плавными (см. ниже).

Чтобы достичь такого эффекта, каждый пиксель сопоставляется с направлением нормали, обозначающим его ориентацию. И оно используется для вычисления освещения вместо истинной ориентации меша.
Считывая направления нормалей из кажущейся случайной текстуры, мы смогли имитировать зернистость. Несмотря на физическую неточность, она всё равно выглядит правдоподобно.
Волны на песке
Однако песчаные дюны демонстрируют и другую особенность, которую невозможно игнорировать: волны. На каждой дюне есть дюны поменьше, появляющиеся из-за воздействия ветра и удерживаемые вместе трением отдельных песчинок.
Эти волны очень заметны и видны на большинстве дюн. На показанной ниже фотографии, сделанной в Омане, видно, что ближняя часть дюны имеет выраженный волнистый узор.

Эти волны значительно изменяются в зависимости не только от формы дюны, но и от состава, направления и скорости ветра. У большинства дюн с острым пиком волны присутствуют только с одной стороны (см. ниже).

Представленный в туториале эффект рассчитан на более плавные дюны, имеющие волны по обеим сторонам. Это не всегда физически точно, но достаточно реалистично для того, чтобы быть правдоподобным, и является хорошим первым шагом к более сложным реализациям.
Реализация волн
Существует множество способов реализации волн. Наименее затратным будет простое рисование их на текстуре, но в туториале мы хотим достичь иного. Причина проста: волны не «плоские» и должны правильно взаимодействовать со светом. Если просто нарисовать их, то невозможно будет добиться реалистичного эффекта при движении камеры (или солнца).
Ещё одним способом добавления волн является изменение геометрии модели дюны. Но повышать сложность модели не рекомендуется, потому что это сильно влияет на общую производительность.
Как мы видели в части про нормали песка, обойти эту проблему можно при помощи карт нормалей. По сути, они отрисовываются на поверхности как традиционные текстуры, но используются в вычислении освещения для имитации более сложной геометрии.
То есть задача превратилась в другую: как создать эти карты нормалей. Ручная отрисовка будет слишком затратной по времени. Кроме того, при каждом изменении дюны нужно будет перерисовывать волны заново. Это значительно замедлит процесс создания ресурсов, чего стремятся избегать многие технические художники.
Гораздо более эффективным и оптимальным решением будет добавление волн процедурным образом. Это значит, что направления нормалей дюны изменяются на основании локальной геометрии, чтобы учесть не только песчинки, но и волны.
Так как волны нужно имитировать на 3D-поверхности, будет логичнее реализовать изменение направления нормалей для каждого пикселя. Для этого проще использовать бесшовную карту нормалей с волновым паттерном. Затем эта карта будет скомбинирована с уже имеющейся картой нормалей, ранее использованной для песка.
Карты нормалей
До этого момента мы встречались с тремя разными нормалями:
- Нормаль геометрии: ориентация каждой грани 3D-модели, которая хранится непосредственно в вершинах;
- Нормаль песка: вычисляется при помощи текстуры шума;
- Нормаль волн: новый эффект, обсуждаемый в этой части.
На примере ниже, взятом со страницы Unity Surface Shader examples, демонстрируется стандартный способ перезаписи нормали 3D-модели. Для этого требуется изменить значение
o.Normal, что обычно выполняется после сэмплирования текстуры (чаще всего называемой картой нормалей). Shader "Example/Diffuse Bump" {
Properties {
_MainTex ("Texture", 2D) = "white" {}
_BumpMap ("Bumpmap", 2D) = "bump" {}
}
SubShader {
Tags { "RenderType" = "Opaque" }
CGPROGRAM
#pragma surface surf Lambert
struct Input {
float2 uv_MainTex;
float2 uv_BumpMap;
};
sampler2D _MainTex;
sampler2D _BumpMap;
void surf (Input IN, inout SurfaceOutput o) {
o.Albedo = tex2D (_MainTex, IN.uv_MainTex).rgb;
o.Normal = UnpackNormal (tex2D (_BumpMap, IN.uv_BumpMap));
}
ENDCG
}
Fallback "Diffuse"
}Точно такую же технику мы использовали для замены нормали геометрии нормалью песка.
Что такое UnpackNormal?
Каждый пиксель карты нормалей обозначает направление нормали. Это единичный вектор (вектор с длиной 1), указывающий в направлении, куда должна быть ориентирована поверхность. Компоненты X, Y и Z направления нормали хранится в каналах R, G и B карты нормалей.
Компоненты единичных векторов находятся в интервале от до
до  . Однако хранящиеся в текстуре значения находятся в интервале от
. Однако хранящиеся в текстуре значения находятся в интервале от  до
до  . Это означает, что перед копированием в текстуру значения нужно «сжать» в другой интервал и «растянуть» их перед использованием. Эти два этапа называются упаковкой нормалей (normal packing) и распаковкой нормалей (normal unpacking). Их можно выполнить при помощи этих очень простых уравнений:
. Это означает, что перед копированием в текстуру значения нужно «сжать» в другой интервал и «растянуть» их перед использованием. Эти два этапа называются упаковкой нормалей (normal packing) и распаковкой нормалей (normal unpacking). Их можно выполнить при помощи этих очень простых уравнений:
и обратных им:
В Unity есть встроенная функция для уравнений (2), которая называется
Подробнее об этом можно почитать на странице Normal Map Technical Details в вики сайта polycount.
Компоненты единичных векторов находятся в интервале от
и обратных им:
В Unity есть встроенная функция для уравнений (2), которая называется
UnpackNormal. Её часто используют для извлечения векторов нормалей из карт нормалей.Подробнее об этом можно почитать на странице Normal Map Technical Details в вики сайта polycount.
Крутизна дюн
Однако первая сложность связана с тем, что форма волн изменяется в зависимости остроты дюн. Невысокие, плоские дюны имеют небольшие волны; на крутых дюнах волновые паттерны более отчётливы. Это значит, что нужно учитывать крутизну дюны.
Проще всего обойти эту проблему, создав две разные карты нормалей, соответственно для плоских и крутых дюн. Основная идея заключается в том, чтобы выполнять смешение между этими двумя картами нормалей на основании крутизны дюны.

Карта нормалей для крутой дюны

Карта нормалей для плоской дюны
Карты нормалей и синий канал
Многие карты нормалей обрабатывают синий канал немного иначе, чем остальные два.
Так получилось, потому что хранящаяся в нём информация по сути является избыточной. Единичные векторы должны иметь единичную длину, то есть после определения двух размерностей (X и Y) значение третьей (Z) полностью определено.
и это значит:
Это отражено непосредственно в функции
По умолчанию Unity хранит карты нормалей в формате DXT5nm, который использует вместо красного и зелёного каналов (
Подробнее о других способах хранения нормалей можно почитать в статье Normal Map Compression в вики сайта polycount.
Так получилось, потому что хранящаяся в нём информация по сути является избыточной. Единичные векторы должны иметь единичную длину, то есть после определения двух размерностей (X и Y) значение третьей (Z) полностью определено.
и это значит:
Это отражено непосредственно в функции
UnpackNormal движка Unity. В зависимости от используемого Shader API она извлекает информацию нормалей из трёх или двух каналов.inline fixed3 UnpackNormal(fixed4 packednormal)
{
#if defined(SHADER_API_GLES) defined(SHADER_API_MOBILE)
return packednormal.xyz * 2 - 1;
#else
fixed3 normal;
normal.xy = packednormal.wy * 2 - 1;
normal.z = sqrt(1 - normal.x*normal.x - normal.y * normal.y);
return normal;
#endif
}По умолчанию Unity хранит карты нормалей в формате DXT5nm, который использует вместо красного и зелёного каналов (
packednormal.xy) альфа-канал и зелёный канал (packednormal.wy).Подробнее о других способах хранения нормалей можно почитать в статье Normal Map Compression в вики сайта polycount.
Почему карты нормалей кажутся сиреневыми?
Если вы раньше пользовались картами нормалей, то знаете, что многие из них преимущественно сиреневатые.
Когда карты нормалей кодируют направления нормалей в касательном пространстве, каждый вектор обозначает новую ориентацию поверхности на относительно действительной ориентации геометрии. Это означает, что направленный вверх вектор нормали![$\left[0, 0, 1\right]$](https://habrastorage.org/getpro/habr/formulas/3d8/a3c/660/3d8a3c660c27759d949fec941d9fe266.svg) не вносит никаких изменений в способ вычисления освещения.
не вносит никаких изменений в способ вычисления освещения.
При кодировании в цвет вектор![$\left[0, 0, 1\right]$](https://habrastorage.org/getpro/habr/formulas/3d8/a3c/660/3d8a3c660c27759d949fec941d9fe266.svg) преобразуется в
преобразуется в ![$\left[0.5, 0.5, 1\right]$](https://habrastorage.org/getpro/habr/formulas/aaa/195/a84/aaa195a845af12eb4e5bbab7062244a2.svg) , что и в самом деле соответствует сиреневому цвету в цветовом пространстве RGB.
, что и в самом деле соответствует сиреневому цвету в цветовом пространстве RGB.
Карты нормалей часто изменят нормали поверхностей только на небольшую величину; это означает, что в среднем они примерно находятся в окрестностях![$\left[0, 0, 1\right]$](https://habrastorage.org/getpro/habr/formulas/3d8/a3c/660/3d8a3c660c27759d949fec941d9fe266.svg) .
.
Кроме того, некоторые карты нормалей не позволяют векторам нормалей указывать «внутрь». Это значит, что компонент B часто находится не в интервале от до
до  , а в интервале от
, а в интервале от  до
до  . Поэтому все пиксели в готовой карте нормалей имеют хотя бы небольшой оттенок синего.
. Поэтому все пиксели в готовой карте нормалей имеют хотя бы небольшой оттенок синего.
Когда карты нормалей кодируют направления нормалей в касательном пространстве, каждый вектор обозначает новую ориентацию поверхности на относительно действительной ориентации геометрии. Это означает, что направленный вверх вектор нормали
При кодировании в цвет вектор
Карты нормалей часто изменят нормали поверхностей только на небольшую величину; это означает, что в среднем они примерно находятся в окрестностях
Кроме того, некоторые карты нормалей не позволяют векторам нормалей указывать «внутрь». Это значит, что компонент B часто находится не в интервале от
Крутизну можно вычислить при помощи скалярного произведения, которое часто применяется в кодировании шейдеров для вычисления степени «параллельности» двух направлений. В данном случае мы берём направление нормали геометрии (ниже показана синим) и сравниваем её с вектором, указывающим в небо (ниже показан жёлтым). Скалярное произведение этих двух векторов возвращает значения, близкие к

Однако мы сталкиваемся с первой проблемой — в этой операции участвует два вектора. Вектор нормали, получаемый из функции
surf при помощи o.Normal, выражен в касательном пространстве. Это значит, что система координат, использованная для кодирования направления нормали, относительна к локальной геометрии поверхности (см. ниже). Мы вкратце касались этой темы в части про нормали песка.
Вектор же, указывающий в небо, выражен в мировом пространстве. Чтобы получить правильное скалярное произведение, оба вектора нужно выразить в одной системе координат. Это означает, что нам нужно преобразовать один из них, чтобы оба были выражены в одном пространстве.
К счастью, нам на помощь приходит Unity с функцией
WorldNormalVector, позволяющей преобразовать вектор нормали из касательного пространства в мировое пространство. Чтобы эта функция заработала, нам нужно изменить структуру Input, чтобы в неё были включены float3 worldNormal и INTERNAL_DATA:struct Input
{
...
float3 worldNormal;
INTERNAL_DATA
};Это объясняется в статье из документации Unity Writing Surface Shaders, где говорится:
INTERNAL_DATA— содержит вектор нормали мирового пространства, если поверхностный шейдер выполняет запись вo.Normal.
Чтобы получить вектор нормали из попиксельной карты нормалей, используйтеWorldNormalVector (IN, o.Normal).
Часто это становится основным источником проблем при написании поверхностных шейдеров. По сути, значение
o.Normal, доступное в функции surf, меняется в зависимости от того, как используется. Если вы только считываете его, o.Normal содержит вектор нормали текущего пикселя в мировом пространстве. Если вы изменяете его значение, o.Normal находится в касательном пространстве.Если вы выполняете запись в
o.Normal, но вам всё равно нужен доступ к нормали в мировом пространстве (как в нашем случае), тогда можно использовать WorldNormalVector (IN, o.Normal). Однако для этого нужно внести небольшое изменение в показанную выше структуру Input.
Что такое INTERNAL_DATA?
Значение
Чтобы понять его влияние, необходимо разобраться с тем, что делает функция
Если не вдаваться в дебри математики, то замену базиса можно реализовать простым умножением 3D-вектора на специально созданную матрицу 3×3. Эта матрица, как можно догадаться, называется матрицей преобразования из касательного в мировое пространство (tangent to world matrix), что Unity сокращает до TtoW.
Данные
Вы увидите, что
Матрица включается не как
В скомпилированном коде шейдера также можно найти определение
Это можно было сделать с помощью оператора матричного умножения
На самом деле, это эквивалентно:
Подробнее о математике наложения нормалей можно узнать из статьи на сайте LearnOpenGL.
INTERNAL_DATA не очень хорошо объяснено в документации Unity.Чтобы понять его влияние, необходимо разобраться с тем, что делает функция
WorldNormalVector. Она получает вектор, выраженный в касательном пространстве, и преобразует его в мировое пространство. Такая смена системы координат в линейной алгебре называется заменой базиса (подробнее в Википедии).Если не вдаваться в дебри математики, то замену базиса можно реализовать простым умножением 3D-вектора на специально созданную матрицу 3×3. Эта матрица, как можно догадаться, называется матрицей преобразования из касательного в мировое пространство (tangent to world matrix), что Unity сокращает до TtoW.
Данные
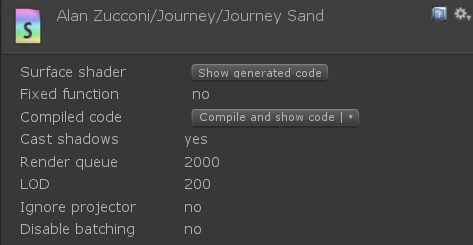
INTERNAL_DATA добавляют матрицу TtoW к структуре Input. Это легко можно увидеть, открыв скомпилированный код шейдера с помощью кнопки «Show generated code» в инспекторе:
Вы увидите, что
INTERNAL_DATA — это сокращение от следующего макроса, который и в самом деле содержит матрицу TtoW:#define INTERNAL_DATA
half3 internalSurfaceTtoW0;
half3 internalSurfaceTtoW1;
half3 internalSurfaceTtoW2;Матрица включается не как
half3x3, а как три отдельные строки half3.В скомпилированном коде шейдера также можно найти определение
WorldNormalVector, которое является макросом, просто выполняющим умножение входящего вектора нормали (выраженного в касательном пространстве) на матрицу TtoW:#define WorldNormalVector(data,normal)
fixed3
(
dot(data.internalSurfaceTtoW0, normal),
dot(data.internalSurfaceTtoW1, normal),
dot(data.internalSurfaceTtoW2, normal)
)Это можно было сделать с помощью оператора матричного умножения
mul, но поскольку матрица TtoW разделена на три отдельных строки, было использовано скалярное произведение.На самом деле, это эквивалентно:
Подробнее о математике наложения нормалей можно узнать из статьи на сайте LearnOpenGL.
Реализация
Фрагмент представленного ниже кода преобразует нормаль из касательного в мировое пространство и вычисляет крутизну относительно направления «вверх».
// Calculates normal in world space
float3 N_WORLD = WorldNormalVector(IN, o.Normal);
float3 UP_WORLD = float3(0, 1, 0);
// Calculates "steepness"
// => 0: steep (90 degrees surface)
// => 1: shallow (flat surface)
float steepness = saturate(dot(N_WORLD, UP_WORLD));Теперь, когда мы вычислили крутизну дюны, можно использовать её для смешения двух карт нормалей. Сэмплируются обе карты нормалей, и плоская, и крутая (в коде ниже они называются
_ShallowTex и _SteepTex). Затем они смешиваются на основании значения steepness:float2 uv = W.xz;
// [0,1]->[-1,+1]
float3 shallow = UnpackNormal(tex2D(_ShallowTex, TRANSFORM_TEX(uv, _ShallowTex)));
float3 steep = UnpackNormal(tex2D(_SteepTex, TRANSFORM_TEX(uv, _SteepTex )));
// Steepness normal
float3 S = normalerp(steep, shallow, steepness);Как говорилось в части о нормалях песка, правильно комбинировать карты нормалей довольно сложно, и это невозможно сделать при помощи
lerp. В данном случае правильнее использовать slerp, но вместо неё используется менее затратная функция под названием normalerp.Смешение волн
Если мы используем показанный выше код, то результаты могут нас разочаровать. Так происходит потому, что дюны имеют очень небольшую крутизну, что приводит к слишком сильному смешиванию двух текстур нормалей. Чтобы исправить это, мы можем применить к крутизне нелинейное преобразование, что повысит резкость смешения:
// Steepness to blending
steepness = pow(steepness, _SteepnessSharpnessPower);При смешении двух текстур для регулирования их резкости и контрастности часто используется
pow. Мы узнали, как и почему это работает в моём туториале Physically Based Rendering.Ниже мы видим два градиента. На верхнем представлены цвета от чёрного к белому, линейно интерполированные по оси X с помощью
c = uv.x. На нижнем тот же градиент представлен при помощи c = pow(uv.x*1.5)*3.0:

Легко заметить, что
pow позволяет создать гораздо более резкий переход между чёрным и белым. Когда мы работаем с текстурами, это уменьшает их наложение друг на друга, создавая более чёткие края.Направление дюн
Всё, что мы сделали ранее, работает идеально. Но нам нужно решить ещё одну последнюю проблему. Волны изменяются в зависимости от крутизны, но не от направления. Как говорилось выше, волны обычно не бывают симметричными из-за того, что ветер преимущественно дует в одном направлении.
Чтобы сделать волны ещё реалистичнее, нам нужно добавить ещё две карты нормалей (см. таблицу ниже). Их можно смешивать в зависимости от параллельности дюны оси X или оси Z.
| Крутая | Плоская | |
| X | крутой x | плоский x |
| Z | крутой z | плоский z |
Здесь нам нужно реализовать вычисление параллельности дюны относительно оси Z. Это можно сделать аналогично вычислению крутизны, но вместо
float3 UP_WORLD = float3(0, 1, 0); можно использовать float3 Z_WORLD = float3(0, 0, 1);.Этот последний шаг я оставлю вам. Если у вас возникнут проблемы, то в конце этого туториала есть ссылка на скачивание полного пакета Unity.
Заключение
Это последняя часть серии туториалов о рендеринге песка игры Journey.
Ниже показано, как далеко мы смогли продвинуться в этой серии:


До и после
Хочу поблагодарить вас за то, что дочитали до конца этот довольно длинный туториал. Надеюсь, вам понравилось изучать и воссоздавать этот шейдер.
Благодарности
Видеоигра Journey была разработана Thatgamecompany и издана Sony Computer Entertainment. Она доступна для PC (Epic Store) и PS4 (PS Store).
3D-модели дюн, фоны и параметры освещения были созданы Jiadi Deng.
3D-модель персонажа Journey найдена на форуме FacePunch (ныне закрытом).
Пакет Unity
Если вы хотите воссоздать этот эффект, то полный пакет Unity доступен для скачивания на Patreon. В нём есть всё необходимое, от шейдеров до 3D-моделей.